Cho x, y, z là ba số thực dương, thoả mãn: xy+yz+xz=xyz.
Chứng minh rằng:
 Giải bởi Vietjack
Giải bởi Vietjack
Đặt
Từ giả thiết, ta có:
Áp dụng bất đẳng thức Cauchy cho ba số thực dương, ta có:
(1).
Tương tự, ta có:
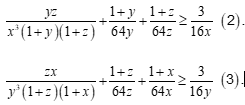
Cộng (1), (2), (3), ta được:
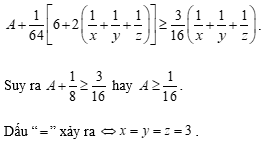
Cho là ba số thực dương thỏa mãn: . Tìm giá trị nhỏ nhất của biểu thức: .
Cho hai số thực dương x, y thỏa mãn xy=1. Tìm giá trị nhỏ nhất của biểu thức:
Cho các số thực x, y thỏa mãn x+y=2. Tìm giá trị nhỏ nhất của biểu thức .
Cho bốn số thực dương x, y, z, t thỏa mãn x+y+z+t=2 Tìm giá trị nhỏ nhất của biểu thức
Cho ba số thực dương x, y, z thỏa mãn x+y+z=3.
Tìm giá trị lớn nhất của biểu thức .
Biết rằng các số x, y thỏa mãn điều kiện x+y=1. Tìm giá trị nhỏ nhất của biểu thức
Cho a, b, c là các số dương thay đổi thỏa mãn:
Tìm giá trị lớn nhất của biểu thức:
Cho các số thực thay đổi luôn thỏa mãn: và .
Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức .
Cho hai số thực dương a, b thỏa mãn . Tìm giá trị lớn nhất của biểu thức
.
Cho hai số thực dương x, y thỏa mãn điều kiện . Tìm giá trị nhỏ nhất của biểu thức
Cho là các số thực không âm thỏa mãn điều kiện và
Tìm giá trị nhỏ nhát của biểu thức
Cho x, y là các số dương thỏa mãn điều kiện . Tìm giá trị nhỏ nhất của biểu thức