Giải bởi Vietjack
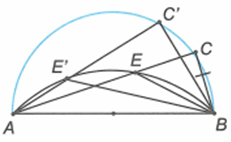
Mà CE = CB (giả thiết) nên suy ra vuông tại C.
(hai góc kề bù).
Mặt khác, AB cố định, nên khi C chuyển động trên đường tròn đường kính AB thì E chuyển động trên cung chứa góc dựng trên đoạn thẳng AB cố định.
Giới hạn: Khi dây AC có độ dài lớn nhất bằng đường kính của đường tròn, thì C trùng với B khi đó E trùng với B. Suy ra B là một điểm của quỹ tích.
Khi dây AC có độ dài nhỏ nhất bằng 0 thì C trùng với A, thì khi đó E trùng với A nên A là một điểm của quỹ tích.
Phần đảo: Lấy E' bất kỳ trên cung chứa góc . Kẻ AE' cắt đường tròn đường kính AB tại C'. Nối BE', BC'.
Ta có: (vì E nằm trên cung chứa góc ).
(hai góc kề bù).
Trong đường tròn đường kính AB có: (góc nội tiếp chắn nửa đường tròn).
Suy ra tam giác E'C'B vuông cân tại C'. Do đó C'E = C'B.
Vậy C' là một điểm thuộc quỹ tích.
Kết luận: Vậy E chuyển động trên một cung chứa góc vẽ trên đoạn AB, nằm trên nửa mặt phẳng bờ AB chứa điểm C.Cho một đường tròn (O) và dây AB cố định, điểm C chuyển động trên cung lớn AB (C khác A và B). Chứng minh rằng tâm I của đường tròn nội tiếp tam giác ABC chuyển động trên một cung tròn cố định.
Cho hình vuông ABCD. Trên cạnh BC lấy điểm E, trên tia đối của tia CD lấy điểm F sao cho CE = CF. Gọi M là giao điểm của hai đường thẳng DE và BF. Tìm quỹ tích của điểm M khi E di động trên cạnh BC.
Cho nửa đường tròn đường kính AB và một dây AC quay quanh A. Trên nửa mặt phẳng bờ AC không chứa B ta vẽ hình vuông ACDE. Hỏi:
a) Điểm D di động trên đường nào?
Cho nửa đường tròn đường kính AB cố định. C là một điểm trên nửa đường tròn, trên dây AC kéo dài lấy điểm D sao cho CD = CB.
a) Tìm quỹ tích các điểm D khi C chạy trên nửa đường tròn đã cho.
