Cho hình vuông ABCD. Trên cạnh BC lấy điểm E, trên tia đối của tia CD lấy điểm F sao cho CE = CF. Gọi M là giao điểm của hai đường thẳng DE và BF. Tìm quỹ tích của điểm M khi E di động trên cạnh BC.
Giải bởi Vietjack
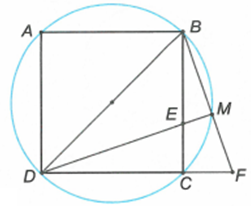
Giới hạn: E trùng với C thì M cũng trùng với C, E trùng với B thì M cũng trùng với B. Suy ra M thuộc cung nhỏ BC.
Phần đảo: Lấy điểm M thuộc quỹ tích và chứng minh CE = CF.
Kết luận: Quỹ tích của điểm M là cung nhỏ BC của đường tròn đường kính BD.
Cho một đường tròn (O) và dây AB cố định, điểm C chuyển động trên cung lớn AB (C khác A và B). Chứng minh rằng tâm I của đường tròn nội tiếp tam giác ABC chuyển động trên một cung tròn cố định.
Cho nửa đường tròn đường kính AB và một dây AC quay quanh A. Trên nửa mặt phẳng bờ AC không chứa B ta vẽ hình vuông ACDE. Hỏi:
a) Điểm D di động trên đường nào?
Cho nửa đường tròn đường kính AB cố định. C là một điểm trên nửa đường tròn, trên dây AC kéo dài lấy điểm D sao cho CD = CB.
a) Tìm quỹ tích các điểm D khi C chạy trên nửa đường tròn đã cho.
