Có tất cả bao nhiêu giá trị nguyên của \(b\) thuộc \(\left( { - 50\,;\,\,50} \right)\) sao cho \({9^a} - \left( {2b - 1} \right){3^a} + {b^2} - b - 6 > 0\) đúng với mọi giá trị \(a \in \left[ {1\,;\,\,2} \right)\)?
 Giải bởi Vietjack
Giải bởi Vietjack
Đặt \(t = {3^a}\), thay vào bất phương trình đã cho ta có \({t^2} - \left( {2b - 1} \right)t + {b^2} - b - 6 > 0\) \((*)\)
Mà \(a \in \left[ {1\,;\,\,2} \right)\) nên \(t \in \left[ {3\,;\,\,9} \right)\), suy ra để bất phương trình đã cho với mọi giá trị \(a \in \left[ {1\,;\,\,2} \right)\) thì \((*)\) đúng với mọi \(t \in \left[ {3\,;\,\,9} \right)\).
Mặt khác: \((*) \Leftrightarrow {t^2} - 2\left( {b - \frac{1}{2}} \right)t + {\left( {b - \frac{1}{2}} \right)^2} - \frac{{25}}{4} > 0\)
\( \Leftrightarrow {\left( {t - b + \frac{1}{2}} \right)^2} > \frac{{25}}{4} \Leftrightarrow \left[ \begin{array}{l}t + \frac{1}{2} - b > \sqrt {\frac{{25}}{4}} = \frac{5}{2}\\t + \frac{1}{2} - b < - \sqrt {\frac{{25}}{4}} = - \frac{5}{2}\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}b < t + \frac{1}{2} - \frac{5}{2} = t - 2\\b > t + \frac{1}{2} + \frac{5}{2} = t + 3\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}b < {\min _{\left[ {3\,;\,\,9} \right)}}\left( {t - 2} \right) = 1\\b > {\max _{\left[ {3\,;\,\,9} \right)}}\left( {t + 3} \right) = 12\end{array} \right.\).
Mà \(b\) nguyên và thuộc \(\left( { - 50\,;\,\,50} \right)\) nên suy ra có \(50 + 38 = 88\) giá trị nguyên thỏa mãn.
Đáp án: 88.
Cho hình chóp \[S.ABC\] có đáy \[ABC\] là tam giác đều, \(SA \bot \left( {ABC} \right).\) Mặt phẳng \(\left( {SBC} \right)\) cách \(A\) một khoảng bằng \(a\) và hợp với mặt phẳng \(\left( {ABC} \right)\) góc \(30^\circ .\) Thể tích của khối chóp \[S.ABC\] bằng
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}.\) Hàm số \(g\left( x \right) = f'\left( {2x + 3} \right) + 2\) có đồ thị là một parabol với tọa độ đỉnh \(I\left( {2\,;\,\, - 1} \right)\) và đi qua điểm \(A\left( {1\,;\,\,2} \right).\) Hỏi hàm số \(y = f\left( x \right)\) nghịch biến trên khoảng nào dưới đây?
Ông A dự định sử dụng hết 6,5m2 kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu mét khối (kết quả làm tròn đến hàng phần trăm)?
Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {x^2}\left( {x + 1} \right)\left( {{x^2} + 2mx + 5} \right),\,\,\forall x \in \mathbb{R}.\) Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số đã cho có đúng một điểm cực trị?
Cho cân bằng sau trong bình kín:
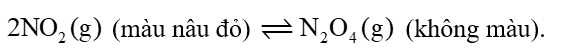
Biết khi hạ nhiệt độ của bình thì màu nâu đỏ nhạt dần. Phản ứng thuận có
Trong không gian \[Oxyz,\] tọa độ điểm đối xứng của điểm \(M\left( {1\,;\,\,2\,;\,\,3} \right)\) qua mặt phẳng \(\left( {Oxz} \right)\) là
Phương trình \({\log _x}2 + {\log _2}x = \frac{5}{2}\) có hai nghiệm \({x_1},{x_2}\,\,\left( {{x_1} < {x_2}} \right).\) Khi đó, giá trị của \(x_1^2 + {x_2}\) bằng
Điền từ/ cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Tố Hữu từng quan niệm “Thơ là chuyện ______. [...] Thơ là tiếng nói đồng ý và đồng tình, tiếng nói đồng chí.”
Chọn từ/cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Cuộc tấn công vào Quảng trường Tự do – quảng trường lớn nhất của Ukraine _______ là trung tâm đời sống công cộng của thành phố, ________ nhiều người Ukraine coi là bằng chứng rằng cuộc tấn công của Nga không chỉ nhằm vào các mục tiêu quân sự mà còn phá vỡ tinh thần của họ.
Cho bảng số liệu:
TỶ LỆ LAO ĐỘNG ĐÃ QUA ĐÀO TẠO
PHÂN THEO THÀNH THỊ VÀ NÔNG THÔN GIAI ĐOẠN 2000-2020
(Đơn vị:%)

(Nguồn: gso.gov.vn)
Một công ty trách nhiệm hữu hạn thực hiện việc trả lương cho các kỹ sư theo phương thức sau: Mức lương của quý làm việc đầu tiên cho công ty là \[13,5\] triệu đồng/quý, và kể từ quý làm việc thứ hai, mức lương sẽ được tăng thêm \[500\,\,000\] đồng mỗi quý. Tổng số tiền lương một kỹ sư nhận được sau ba năm làm việc cho công ty là