Cho hai hàm số \[y = \ln \left| {\frac{{x - 2}}{x}} \right|\]và\(y = \frac{3}{{x - 2}} - \frac{1}{x} + 4m - 2020\). Tổng tất cả các giá trị nguyên của tham số m để hai đồ thị hàm số cắt nhau tại một điểm duy nhất bằng:
A.506
B.1011
C.2020
D.1010
Giải bởi Vietjack
ĐKXĐ: \[x \ne 0,\,\,x \ne 2\]
Xét phương trình hoành độ giao điểm:
\[\begin{array}{*{20}{l}}{\ln \left| {\frac{{x - 2}}{x}} \right| = \frac{3}{{x - 2}} - \frac{1}{x} + 4m - 2020}\\{ \Leftrightarrow \ln \left| {\frac{{x - 2}}{x}} \right| - \frac{3}{{x - 2}} + \frac{1}{x} = 4m - 2020}\end{array}\]
Đặt \[f\left( x \right) = \ln \left| {\frac{{x - 2}}{x}} \right| - \frac{3}{{x - 2}} + \frac{1}{x}\]ta có:
\[\begin{array}{l}f\prime (x) = \frac{2}{{{x^2}}}:\frac{{x - 2}}{x} + \frac{3}{{{{(x - 2)}^2}}} - \frac{1}{{{x^2}}}\\f\prime (x) = \frac{2}{{x(x - 2)}} + \frac{3}{{{{(x - 2)}^2}}} - \frac{1}{{{x^2}}}\\f\prime (x) = \frac{{2x(x - 2) + 3{x^2} - {{(x - 2)}^2}}}{{{x^2}{{(x - 2)}^2}}}\\f\prime (x) = \frac{{2{x^2} - 4x + 3{x^2} - {x^2} + 4x - 4}}{{{x^2}{{(x - 2)}^2}}}\\f\prime (x) = \frac{{4{x^2} - 4}}{{{x^2}{{(x - 2)}^2}}} = 0 \Leftrightarrow x = \pm 1\end{array}\]
BBT:
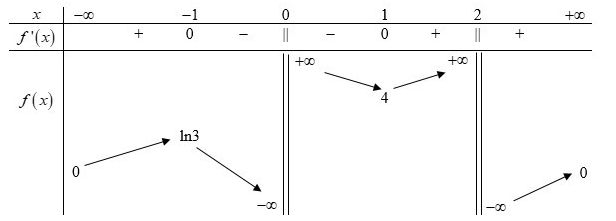
Dựa vào BBT ta thấy để phương trình có nghiệm duy nhất thì
\(\left[ {\begin{array}{*{20}{c}}{4m - 2020 = 0}\\{4m - 2020 = ln3}\\{4m - 2020 = 4}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = 505}\\{m = \frac{{2020 + ln3}}{4}}\\{m = 506}\end{array}} \right. \notin \mathbb{Z}(ktm)\)
Vậy tổng các giá trị của m thỏa mãn yêu cầu bài toán là:\[505 + 506 = 1011\]Đáp án cần chọn là: B
Tiệm cận đứng của đồ thị hàm số \[y = {\log _a}x(0 < a \ne 1)\] là đường thẳng:
Điểm nào sau đây không thuộc đồ thị hàm số \[y = lo{g_a}x(0 < a \ne 1)\;\]?
Tìm tất cả các giá trị thực của tham số m sao cho hàm số \[y = log\left( {{x^2} - 2mx + 4} \right)\]có tập xác định là R
Điểm \[({x_0};{y_0})\;\]thuộc đồ thị hàm số \[y = lo{g_a}x(0 < a \ne 1)\;\] nếu:
Cho ba số thực dương a,b,c khác 1. Đồ thị các hàm số \[y = {\log _a}x,y = {\log _b}x,y = {\log _c}x\] được cho trong hình vẽ sau:
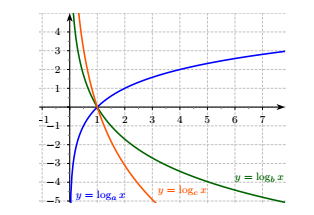
Mệnh đề nào dưới đây đúng?
Đạo hàm hàm số \[y = {\log _{2018}}\left( {2018x + 1} \right)\] là:
Tìm tập giá trị T của hàm số \[f'\left( x \right) = \frac{{1 - \ln x}}{{{x^2}}}\] với \[x \in [1;{e^2}].\]
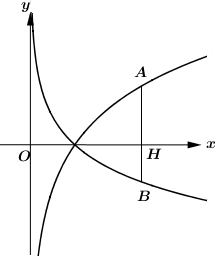
Cho a và b là các số thực dương khác 1. Biết rằng bất kì đường thẳng nào song song với trục tung mà cắt các đồ thị \[y = {\log _a}x,y = {\log _b}x\] và trục hoành lần lượt tại A,B và H phân biệt ta đều có 3HA=4HB (hình vẽ bên dưới). Khẳng định nào sau đây là đúng?
Xét các số thực a, b thỏa mãn a>b>1. Tìm giá trị nhỏ nhất Pmin của biểu thức \[P = \log _{\frac{a}{b}}^2\left( {{a^2}} \right) + 3{\log _b}\frac{a}{b}\].
