Tam giác ABC có các góc \(\widehat B = 30^\circ ,\widehat C = 45^\circ \), AB = 3. Tính cạnh AC.
A. \(\frac{{3\sqrt 6 }}{2}\);
B. \(\frac{{3\sqrt 2 }}{2}\);
C. \(\sqrt 6 \);
D. \(\frac{{2\sqrt 6 }}{3}\).
Giải bởi Vietjack
Đáp án đúng là: B
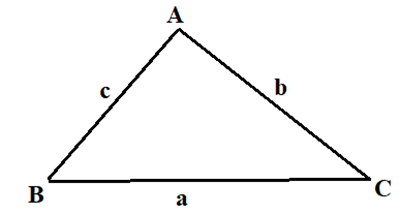
Ta có: \[\frac{b}{{\sin B}} = \frac{c}{{\sin C}} \Rightarrow AC = b = \frac{{c.\sin B}}{{\sin C}} = \frac{{AB.\sin B}}{{\sin C}} = \frac{{3.\sin {{30}^0}}}{{\sin {{45}^0}}} = \frac{{3\sqrt 2 }}{2}\].
Hình bình hành có hai cạnh là 3 và 5, một đường chéo bằng 5. Tìm độ dài đường chéo còn lại.
Tính góc C của tam giác ABC biết a ≠ b và a(a2 – c2) = b(b2 – c2).
Cho \[\cos \alpha = - \frac{4}{5}\] và góc α thỏa mãn 90° < α < 180°. Khi đó.
Nếu 3cosx + 2 sinx = 2 và sinx < 0 thì giá trị đúng của sinx là:
Cho tan α = 2. Giá trị của \(A = \frac{{3\sin \alpha + \cos \alpha }}{{\sin \alpha - \cos \alpha }}\) là :
Cho tam giác ABC có a = 2, \[b = \sqrt 6 \], \[c = \sqrt 3 + 1\]. Tính bán kính R của đường tròn ngoại tiếp.
Biết tanα = 2, giá trị của biểu thức \(M = \frac{{3\sin \alpha - 2\cos \alpha }}{{5\cos \alpha + 7\sin \alpha }}\) bằng:
