Thi thử bài tập trắc nghiệm ôn tập Xác suất thống kê online - Đề 16
-
487 lượt thi
-
30 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Từ các chữ số 0, 1, 2, 3, 4, 5 có thể lập được bao nhiêu số lẻ gồm 4 chữ số khác nhau?
Xem đáp án
Chọn đáp án C
Câu 2:
Từ các chữ số 0, 1, 2, 3, 4, 5 có thể lập được bao nhiêu số chẵn gồm 4 chữ số khác nhau?
Xem đáp án
Chọn đáp án A
Câu 3:
Có bao nhiêu khả năng có thể xảy ra đối với thứ tự giữa các đội trong một giải bóng có 5 đội bóng? (giả sử rằng không có hai đội nào có điểm trùng nhau)?
Xem đáp án
Chọn đáp án A
Câu 6:
Số cách sắp xếp 6 nam sinh và 4 nữ sinh vào một dãy ghế hàng ngang có 10 chỗ ngồi là:
Xem đáp án
Chọn đáp án B
Câu 7:
Sắp xếp năm bạn học sinh An, Bình, Chi, Dũng, Lệ vào một chiếc ghế dài có 5 chỗ ngồi. Số cách sắp xếp sao cho bạn Chi luôn ngồi chính giữa là:
Xem đáp án
Chọn đáp án A
Câu 8:
Sắp xếp năm bạn học sinh An, Bình, Chi, Dũng, Lệ vào một chiếc ghế dài có 5 chỗ ngồi. Hỏi có bao nhiêu cách sắp xếp sao cho bạn An và bạn Dũng luôn ngồi ở hai đầu ghế?
Xem đáp án
Chọn đáp án C
Câu 9:
Sắp xếp năm bạn học sinh An, Bình, Chi, Dũng, Lệ vào một chiếc ghế dài có 5 chỗ ngồi. Hỏi có bao nhiêu cách sắp xếp sao cho bạn An và bạn Dũng không ngồi cạnh nhau?
Xem đáp án
Chọn đáp án C
Câu 10:
Có 3 viên bi đen khác nhau, 4 viên bi đỏ khác nhau, 5 viên bi xanh khác nhau. Hỏi có bao nhiêu cách sắp xếp các viên bi trên thành một dãy sao cho các viên bi cùng màu ở cạnh nhau?
Xem đáp án
Chọn đáp án C
Câu 11:
Cô dâu và chú rể mời 6 người ra chụp ảnh kỉ niệm, người thợ chụp hình có bao nhiêu cách sắp xếp sao cho cô dâu, chú rể đứng cạnh nhau.
Xem đáp án
Chọn đáp án B
Câu 12:
Trên giá sách muốn xếp 20 cuốn sách khác nhau. Có bao nhiêu cách sắp xếp sao cho tập 1 và tập 2 đặt cạnh nhau
Xem đáp án
Chọn đáp án D
Câu 13:
Có bao nhiêu cách sắp xếp 4 người vào 4 ghế ngồi được bố trí quanh một bàn tròn?
Xem đáp án
Chọn đáp án D
Câu 14:
Có 4 nữ sinh tên là Huệ, Hồng, Lan, Hương và 4 nam sinh tên là An, Bình, Hùng, Dũng cùng ngồi quanh một bàn tròn có 8 chỗ ngồi. Hỏi có bao nhiêu cách sắp xếp biết nam và nữ ngồi xen kẽ nhau?
Xem đáp án
Chọn đáp án B
Câu 15:
Một hộp chứa 5 bóng đỏ và 5 bóng xanh. Lấy ngẫu nhiên ra 2 quả bóng. Nếu chúng cùng mầu thì thắng 1, nếu khác màu thì thắng -1 (nghĩa là thua 1$). Gọi X là số tiền thắng sau 1 ván đấu. EX2 = ?
Xem đáp án
Chọn đáp án B
Câu 16:
Có bao nhiêu cách xếp khác nhau cho 6 người ngồi vào 4 chỗ trên một bàn dài?
Xem đáp án
Chọn đáp án D
Câu 17:
Giả sử có bảy bông hoa khác nhau và ba lọ hoa khác nhau. Hỏi có bao nhiêu cách cắm ba bông hoa vào ba lọ đã cho (mội lọ cắm một bông)?
Xem đáp án
Chọn đáp án C
Câu 18:
Có bao nhiêu cách cắm 3 bông hoa vào 5 lọ khác nhau (mội lọ cắm không quá một một bông)?
Xem đáp án
Chọn đáp án A
Câu 19:
Có bao nhiêu cách mắc nối tiếp 4 bóng đèn được chọn từ 6 bóng đèn khác nhau?
Xem đáp án
Chọn đáp án B
Câu 20:
Trong trận chung kết bóng đá phải phân định thắng thua bằng đá luân lưu 11 mét. Huấn luyện viên mỗi đội cần trình với trọng tài một danh sách sắp thứ tự 5 cầu thủ trong số 11 cầu thủ để đá luân lưu 5 quả 11 mét. Hãy tính xem huấn luyện viên của mỗi đội có bao nhiêu cách lập danh sách gồm 5 cầu thủ
Xem đáp án
Chọn đáp án C
Câu 21:
Tuổi thọ của một loại thiết bị điện tử (đo bằng giờ) là một biến ngẫu nhiên có hàm mật độ cho bởi 
P(X > 20) = ?
Xem đáp án
Chọn đáp án D
Câu 22:
Giả sử có 8 vận động viên tham gia chạy thi. Nếu không kể trường hợp có hai vận động viên về đích cùng lúc thì có bao nhiêu kết quả có thể xảy ra đối với các vị trí nhất, nhì, ba?
Xem đáp án
Chọn đáp án A
Câu 23:
Trong một ban chấp hành đoàn gồm 7 người, cần chọn ra 3 người vào ban thường vụ. Nếu cần chọn ban thường vụ gồm ba chức vụ Bí thư, Phó bí thư, Ủy viên thường vụ thì có bao nhiêu cách chọn?
Xem đáp án
Chọn đáp án A
Câu 24:
Một cuộc thi có 15 người tham dự, giả thiết rằng không có hai người nào có điểm bằng nhau. Nếu kết quả của cuộc thi là việc chọn ra các giải nhất, nhì, ba thì có bao nhiêu kết quả có thể?
Xem đáp án
Chọn đáp án A
Câu 25:
Trong một dạ hội cuối năm ở một cơ quan, ban tổ chức phát ra 100 vé xổ số đánh số từ 1 đến 100 cho 100 người. Xổ số có 4 giải: 1 giải nhất, 1 giải nhì, 1 giải ba, 1 giải tư. Kết quả là việc công bố ai trúng giải nhất, giải nhì, giải ba, giải tư. Hỏi có bao nhiêu kết quả có thể?
Xem đáp án
Chọn đáp án B
Câu 26:
Trong một dạ hội cuối năm ở một cơ quan, ban tổ chức phát ra 100 vé xổ số đánh số từ 1 đến 100 cho 100 người. Xổ số có 4 giải: 1 giải nhất, 1 giải nhì, 1 giải ba, 1 giải tư. Kết quả là việc công bố ai trúng giải nhất, giải nhì, giải ba, giải tư. Hỏi có bao nhiêu kết quả có thể nếu biết rằng người giữ vé số 47 được giải nhất?
Xem đáp án
Chọn đáp án C
Câu 27:
Trong một dạ hội cuối năm ở một cơ quan, ban tổ chức phát ra 100 vé xổ số đánh số từ 1 đến 100 cho 100 người. Xổ số có 4 giải: 1 giải nhất, 1 giải nhì, 1 giải ba, 1 giải tư. Kết quả là việc công bố ai trúng giải nhất, giải nhì, giải ba, giải tư. Hỏi có bao nhiêu kết quả có thể nếu biết rằng người giữ vé số 47 trúng một trong bốn giải?
Xem đáp án
Chọn đáp án D
=?
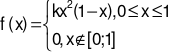
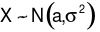
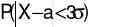