(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
139 lượt thi
-
15 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Cho hàm số \({\rm{f}}({\rm{x}}) = {\rm{a}}{{\rm{x}}^3} + {\rm{b}}{{\rm{x}}^2} + {\rm{cx}} + {\rm{d}}({\rm{a}},{\rm{b}},{\rm{c}},{\rm{d}} \in \mathbb{R},{\rm{a}} \ne 0)\) có bảng xét dấu của đạo hàm dưới đây
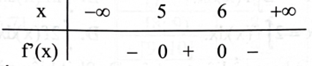
Hàm số đã cho đồng biến trên khoảng
 Xem đáp án
Xem đáp án
Chọn đáp án B
Câu 2:
 Xem đáp án
Xem đáp án
Chọn đáp án A
Câu 3:
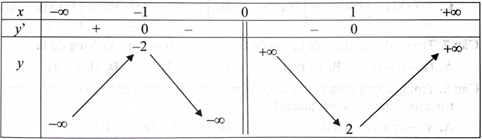
Cho hàm số \({\rm{f}}({\rm{x}})\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình bên. Giá trị lớn nhất của \({\rm{f}}({\rm{x}})\) trên đoạn [1;2] bằng
![Cho hàm số \({\rm{f}}({\rm{x}})\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình bên. Giá trị lớn nhất của \({\rm{f}}({\rm{x}})\) trên đoạn [1;2] bằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/09/blobid2-1727150158.png)
 Xem đáp án
Xem đáp án
Chọn đáp án C
Câu 4:
Cho hàm số \(f(x) = \frac{{ax + b}}{{cx + d}}\) \(({\rm{a}},{\rm{b}},{\rm{c}},{\rm{d}} \in \mathbb{R},{\rm{ac}} \ne 0)\) có đồ thị như hình bên. Đường tiệm cận đứng của đồ thị hàm số là
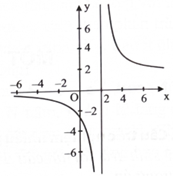
 Xem đáp án
Xem đáp án
Chọn đáp án D
Câu 5:
 Xem đáp án
Xem đáp án
Chọn đáp án C
Câu 6:
 Xem đáp án
Xem đáp án
Chọn đáp án D
Câu 7:
 Xem đáp án
Xem đáp án
Chọn đáp án A
Câu 8:
 Xem đáp án
Xem đáp án
Chọn đáp án C
Câu 9:
 Xem đáp án
Xem đáp án
Chọn đáp án D
Câu 10:
 Xem đáp án
Xem đáp án
Chọn đáp án A
Câu 11:
 Xem đáp án
Xem đáp án
Chọn đáp án D
Câu 12:
Khi thống kê kết quả thi thử của 100 học sinh ở một trung tâm giáo dục, người ta được bảng thống kê tần số ghép nhóm như hình bên. Số trung bình của mẫu số liệu là
|
Điểm |
Giá trị đại diện |
Tần số |
|
\([3;4)\) |
3,5 |
2 |
|
\([4;5)\) |
4,5 |
7 |
|
\([5;6)\) |
5,5 |
21 |
|
\([6;7)\) |
6,5 |
26 |
|
\([7;8)\) |
7,5 |
29 |
|
\([8;9)\) |
8,5 |
12 |
|
[9 ; 10] |
9,5 |
3 |
|
|
|
n = 100 |
 Xem đáp án
Xem đáp án
Chọn đáp án D
Câu 13:
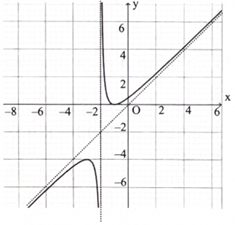
d) Hàm số đã cho có đồ thị như hình sau:
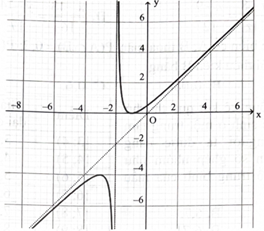
 Xem đáp án
Xem đáp án
d) Hàm số đã cho có đồ thị như hình sau:
Câu 14:
Người ta thả một số lá bèo vào một hồ nước. Sau 10 giờ, số lượng lá bèo sẽ sinh sôi kín cả mặt hồ. Biết rằng sau mỗi giờ, số lượng lá bèo tăng gấp 10 lần số lượng lá bèo trước đó và tốc độ tăng không đổi. Sau ít nhất mấy giờ thì số lá bèo phủ kín hơn một phần tư hồ (làm tròn kết quả đến hàng đơn vị)?
 Xem đáp án
Xem đáp án
Đáp số: 10.
Gọi M là số lượng lá bèo lúc đầu được thả vào hồ nước.
Sau 1 giờ thì hồ có 10 M lá bèo. Sau 2 giờ thì hồ có \(10(10{\rm{M}}) = {10^2}{\rm{M}}\) lá bèo.
Sau k giờ thì hồ có \({10^{\rm{k}}}{\rm{M}}\) lá bèo. Sau 10 giờ thì có \({10^{10}}{\rm{M}}\) lá bèo (đầy hồ). \(\frac{1}{4}\) hồ là \(\frac{{{{10}^{10}} \cdot {\rm{M}}}}{4}\) lá bèo.
Cho \({10^{\rm{k}}}.{\rm{M}} = \frac{{{{10}^{10}} \cdot {\rm{M}}}}{4} \Rightarrow {\rm{k}} = \log \left( {\frac{{{{10}^{10}}}}{4}} \right) \approx 9,4\) (giờ).
Câu 15:
Một hộp chứa 15 tấm thẻ cùng loại được đánh số lần lượt từ 1 đến 15. Bạn An lấy ra lần lượt 3 thẻ từ hộp. Thẻ lấy ra không được hoàn lại hộp. Tính xác suất của biến cố: "Lần thứ ba An lấy được thẻ ghi số lẻ, biết rằng lần hai An lấy được thẻ ghi số chẵn" (làm tròn kết quả đến hàng phần trăm).
 Xem đáp án
Xem đáp án
Đáp số: 0,57.
Gọi Ai là biến cố lần thứ i lấy được thẻ chẵn ( \({\rm{i}} = 1,2,3\) ). Ta cần tính
\({\rm{P}}\left( {\overline {{{\rm{A}}_3}} \mid {{\rm{A}}_2}} \right) = \frac{{{\rm{P}}\left( {\overline {{{\rm{A}}_3}} \;{{\rm{A}}_2}} \right)}}{{{\rm{P}}\left( {{{\rm{A}}_2}} \right)}}\)
\({\rm{P}}\left( {{{\rm{A}}_1}} \right) = \frac{7}{{15}},{\rm{P}}\left( {\overline {{{\rm{A}}_1}} } \right) = \frac{8}{{15}},{\rm{P}}\left( {{{\rm{A}}_2}\mid {{\rm{A}}_1}} \right) = \frac{6}{{14}} = \frac{3}{7},{\rm{P}}\left( {{{\rm{A}}_2}\mid \overline {{{\rm{A}}_1}} } \right) = \frac{7}{{14}} = \frac{1}{2}\)
\({\rm{P}}\left( {{{\rm{A}}_2}} \right) = {\rm{P}}\left( {{{\rm{A}}_1}} \right){\rm{P}}\left( {{{\rm{A}}_2}\mid {{\rm{A}}_1}} \right) + {\rm{P}}\left( {\overline {{{\rm{A}}_1}} } \right){\rm{P}}\left( {{{\rm{A}}_2}\mid \overline {{{\rm{A}}_1}} } \right) = \frac{7}{{15}} \cdot \frac{3}{7} + \frac{8}{{15}} \cdot \frac{1}{2} = \frac{7}{{15}}\)
\({\rm{P}}\left( {\overline {{{\rm{A}}_3}} \;{{\rm{A}}_2}} \right) = {\rm{P}}\left( {\overline {{{\rm{A}}_3}} \;{{\rm{A}}_2}\;{{\rm{A}}_1}} \right) + {\rm{P}}\left( {\overline {{{\rm{A}}_3}} \;{{\rm{A}}_2}\overline {{{\rm{A}}_1}} } \right)\)
(sử dụng tính chất \({\rm{P}}({\rm{A}}) = {\rm{P}}\left( {{\rm{A}}{{\rm{A}}_1}} \right) + {\rm{P}}\left( {{\rm{A}}\overline {{{\rm{A}}_1}} } \right)\) với \(\left. {{\rm{A}} = \overline {{{\rm{A}}_3}} \;{{\rm{A}}_2}} \right)\).
\({\rm{P}}\left( {\overline {{{\rm{A}}_3}} \;{{\rm{A}}_2}\;{{\rm{A}}_1}} \right) = {\rm{P}}\left( {\overline {{{\rm{A}}_3}} \mid {{\rm{A}}_2}\;{{\rm{A}}_1}} \right){\rm{P}}\left( {{{\rm{A}}_2}\;{{\rm{A}}_1}} \right) = {\rm{P}}\left( {\overline {{{\rm{A}}_3}} \mid {{\rm{A}}_2}\;{{\rm{A}}_1}} \right){\rm{P}}\left( {{{\rm{A}}_2}\mid {{\rm{A}}_1}} \right){\rm{P}}\left( {{{\rm{A}}_1}} \right)\)
\( = \frac{8}{{13}} \cdot \frac{6}{{14}} \cdot \frac{7}{{15}}\)
\({\rm{P}}\left( {\overline {{{\rm{A}}_3}} \;{{\rm{A}}_2} \cdot \overline {{{\rm{A}}_1}} } \right) = {\rm{P}}\left( {\overline {{{\rm{A}}_3}} \mid {{\rm{A}}_2}\overline {{{\rm{A}}_1}} } \right){\rm{P}}\left( {{{\rm{A}}_2}\overline {{{\rm{A}}_1}} } \right) = {\rm{P}}\left( {\overline {{{\rm{A}}_3}} \mid {{\rm{A}}_2}\overline {{{\rm{A}}_1}} } \right){\rm{P}}\left( {{{\rm{A}}_2}\mid \overline {{{\rm{A}}_1}} } \right){\rm{P}}\left( {\overline {{{\rm{A}}_1}} } \right)\)
\( = \frac{7}{{13}} \cdot \frac{7}{{14}} \cdot \frac{8}{{15}}.\)
\({\rm{P}}\left( {\overline {{{\rm{A}}_3}} \mid {{\rm{A}}_2}} \right) = \frac{{{\rm{P}}\left( {\overline {{{\rm{A}}_3}} \;{{\rm{A}}_2}} \right)}}{{{\rm{P}}\left( {{{\rm{A}}_2}} \right)}} = \frac{{{\rm{P}}\left( {\overline {{{\rm{A}}_3}} \;{{\rm{A}}_2}\;{{\rm{A}}_1}} \right) + {\rm{P}}\left( {\overline {{{\rm{A}}_3}} \;{{\rm{A}}_2}\overline {{{\rm{A}}_1}} } \right)}}{{{\rm{P}}\left( {{{\rm{A}}_2}} \right)}} = \frac{{\frac{8}{{13}} \cdot \frac{6}{{14}} \cdot \frac{7}{{15}} + \frac{7}{{13}} \cdot \frac{7}{{14}} \cdot \frac{8}{{15}}}}{{\frac{7}{{15}}}}\)
\( = \frac{{\frac{{7.8}}{{14 \cdot 15}}}}{{\frac{7}{{15}}}} = \frac{8}{{14}} \approx 0,57.\)
