(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
162 lượt thi
-
20 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Chọn đáp án A
Câu 2:
Cho hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }.\) Cặp vectơ nào sau đây là cặp vectơ chỉ phương của mặt phẳng \(({\rm{ABCD}})\) ?
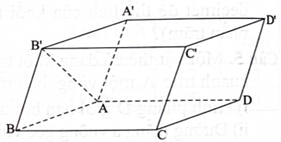
 Xem đáp án
Xem đáp án
Chọn đáp án D
Câu 3:
Cho hàm số \({\rm{f}}({\rm{x}})\) có đồ thị như hình bên. Biết rằng một trong bốn đường thẳng sau đây là đường tiệm cận xiên của đồ thị hàm số, đường đó là đường nào?
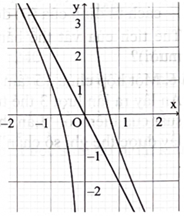
 Xem đáp án
Xem đáp án
Chọn đáp án C
Câu 4:
Cho hàm số \({\rm{f}}({\rm{x}})\) có đồ thị như hình bên. Biết rằng một trong bốn điểm sau đây là tâm đối xứng của đồ thị hàm số, điểm đó là điểm nào?
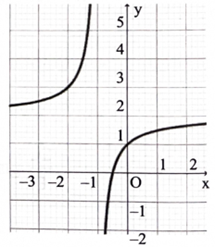
 Xem đáp án
Xem đáp án
Chọn đáp án B
Câu 5:
 Xem đáp án
Xem đáp án
Chọn đáp án D
Câu 6:
 Xem đáp án
Xem đáp án
Chọn đáp án B
Câu 7:
 Xem đáp án
Xem đáp án
Chọn đáp án C
Câu 8:
 Xem đáp án
Xem đáp án
Chọn đáp án D
Câu 9:
 Xem đáp án
Xem đáp án
Chọn đáp án C
Câu 10:
 Xem đáp án
Xem đáp án
Chọn đáp án B
Câu 11:
 Xem đáp án
Xem đáp án
Chọn đáp án A
Câu 12:
 Xem đáp án
Xem đáp án
Chọn đáp án C
Câu 15:
c) Hàm số đồng biến trên khoảng \((0;3).\)
 Xem đáp án
Xem đáp án
c) Hàm số không đồng biến trên khoảng (0;3).
=> Sai
Câu 16:
d) Giá trị lớn nhất của hàm số trên đoạn \([ - 1;3]\) bằng 4.
 Xem đáp án
Xem đáp án
d) Giá trị lớn nhất của hàm số trên đoạn [-1; 3] bằng 4.
=> Đúng
Câu 17:
a) Khi xe dừng hẳn thì vận tốc bằng \(0(\;{\rm{m}}/{\rm{s}}).\)
 Xem đáp án
Xem đáp án
a) Khi xe dừng hẳn thì vận tốc bằng \(0(\;{\rm{m}}/{\rm{s}}).\)
=> Đúng
Câu 18:
d) Quãng đường từ lúc đạp phanh cho đến khi dừng hẳn là 18 m.
 Xem đáp án
Xem đáp án
d) Quãng đường từ lúc đạp phanh cho đến khi dừng hẳn là
\(\int_0^3 {( - 4{\rm{t}} + 12{\rm{t}})} {\rm{dt}} = \left. {\left( { - 2{{\rm{t}}^2} + 12{\rm{t}}} \right)} \right|_0^3 = 18(\;{\rm{m}})\)
=> Đúng
Câu 19:
Nền nhà tầng một của một hội trường có độ cao 1 m so với mặt đất. Từ nền nhà tầng 1 lên nền nhà tầng 2 có một cầu thang 21 bậc, độ cao của các bậc so với mặt đất theo thứ tự lập thành một cấp số cộng \(\left( {{u_n}} \right)\) có 21 số hạng: \({{\rm{u}}_1} = 1,\;{\rm{d}} = 0,16\) (đơn vị là mét). Độ cao của bậc thứ 8 so với mặt đất là bao nhiêu mét?
 Xem đáp án
Xem đáp án
Đáp số: 2,12.
Độ cao của bậc thứ 8 so với mặt đất là \({\rm{u}}8 = {\rm{u}}1 + 7\;{\rm{d}} = 1 + 7 \cdot 0,16 = 2,12(\;{\rm{m}}).\)
Câu 20:
E-mail Filter là một phần mềm chặn email quảng cáo. Nếu một email là thư quảng cáo, phần mềm sẽ chuyển nó vào thư mục Spam với xác suất là 0,9. Ngược lại, nếu một email không là thư quảng cáo, phần mềm có thể chuyển nó vào thư mục Spam với xác suất 0,05. Thống kê trong một số lượng lớn email bị chuyển vào thư mục Spam thì thấy tỉ lệ thư quảng cáo là 72%. Xác suất một email là thư quảng cáo là bao nhiêu? (Làm tròn kết quả đến hàng phần trăm)
 Xem đáp án
Xem đáp án
Đáp số: \({\bf{0}},{\bf{13}}.\)
Chọn ngẫu nhiên một email. Gọi A là biến cố email đó là thư quảng cáo và B là biến cố E -mail Filter chuyển email đó vào thư mục Spam.
Ta có \({\rm{P}}({\rm{B}}\mid {\rm{A}}) = 0,9;{\rm{P}}({\rm{B}}\mid \overline {\rm{A}} ) = 0,05;{\rm{P}}({\rm{A}}\mid {\rm{B}}) = 0,72.\)
Áp dụng công thức Bayes, ta có: \({\rm{P}}({\rm{A}}\mid {\rm{B}}) = \frac{{{\rm{P}}({\rm{B}}\mid {\rm{A}}){\rm{P}}({\rm{A}})}}{{{\rm{P}}({\rm{B}}\mid {\rm{A}}){\rm{P}}({\rm{A}}) + {\rm{P}}({\rm{B}}\mid \overline {\rm{A}} ){\rm{P}}(\overline {\rm{A}} )}}.\)
Đặt \(P(A) = p \in [0;1]\), ta có:
\(0,72 = \frac{{0,9p}}{{0,9p + 0,05(1 - {\rm{p}})}} \Leftrightarrow 0,8(0,85{\rm{p}} + 0,05) = {\rm{p}}.\)
Giải phương trình trên ta được \({\rm{p}} = 0,125.\)
