214 Bài toán thực tế từ đề thi Đại học có lời giải chi tiết (P2)
-
6702 lượt thi
-
35 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 1:
Người ta xây một bể chứa hình trụ tròn với chiều cao bể chứa giảm một nửa so với dự tính ban đầu, nhưng bán kính đáy lại tăng gấp đôi so với dự tính ban đầu. Hỏi thể tích bể chứa sau khi xây dựng xong và thể tích dự tính ban đầu thay đổi như thế nào?
 Xem đáp án
Xem đáp án
Đáp án B
Câu 2:
Người ta cưa một cây gỗ hình trụ tròn dài 1m, với đường kính cây gỗ là 60cm thành một hộp gỗ hình chữ nhật dài 1m. Người ta phải tìm cách để hộp đó có thể tích lớn nhất. Thể tích lớn nhất đó bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án A
Hộp gỗ đó có thể tích lớn nhất khi và chỉ khi hình chữ nhật nội tiếp đường tròn có đường kính 0,6 (mét) phải có diện tích lớn nhất. Gọi kích thước hai cạnh chữ nhật đó là a, b nên
Câu 3:
Một người vay ngân hàng 500 triệu, với điều khoản mỗi tháng phải trả 10 triệu tiền gốc và 1% tiền lãi của khoản vay còn lại của tháng trước đó. Hỏi tới khi trả hết 500 triệu tiền vay thì người đó phải trả tất cả bao nhiêu tiền lãi?
 Xem đáp án
Xem đáp án
Đáp án C
Câu 4:
Mức thu nhập bình quân đầu người của quốc gia V hiện tại là 2000USD/1 người/1 năm. Biết mức tăng trưởng GDP (tổng thu nhập quốc dân) của quốc gia đó là 6%/năm và mức gia tăng dân số của quốc gia đó là 1%/năm. Hỏi phải ít nhất bao nhiêu năm nữa mức thu nhập bình quân đầu người của quốc gia V lớn hơn 10.000USD?
 Xem đáp án
Xem đáp án
Đáp án B
Câu 5:
Một ô tô đang chuyển động đều với vận tốc 12 m/s thì người lái đạp phanh; từ thời điểm đó ô tô chuyển động chậm dần đều với vận tốc (trong đó t là thời gian tính bằng giây, kể từ lúc đạp phanh). Hỏi trong thời gian 8 giây cuối (tính đến khi xe dừng hẳn) thì ô tô đi được quãng đường bao nhiêu?
 Xem đáp án
Xem đáp án
Chọn đáp án B.
Từ lúc phanh đến khi xư dừng lại hết thời gian là: .
Vậy trong 8s cuối thì 2 giây đầu xe vẫn chuyển động đều quãng đường là: .
Quãng đường vật đi được trong 6 giây cuối khi dừng lại là:
Vậy tổng quãng đường ô tô đi được là: .
Câu 6:
Khi ánh sáng đi qua một môi trường (chẳng hạn như không khí, sương mù,…), cường độ sẽ giảm dần theo quãng đường truyền x, theo công thức , trong đó là cường độ của ánh sáng khi bắt đầu truyền vào môi trường và là hệ số hấp thu của môi trường đó. Biết rằng nước biển có hệ số hấp thu là và người ta tính được rằng khi đi từ độ sâu 2 m xuống đến độ sâu 20 m thì cường độ ánh sáng giảm lần. Số nguyên nào sau đây gần với l nhất?
 Xem đáp án
Xem đáp án
Chọn đáp án B.
Với có hệ số hấp thu là cường độ sẽ giảm dần theo .
Ở độ sâu 2m cường độ sẽ giảm: .
Ở độ sâu 20m cường độ sẽ giảm: .
Theo giả thiết thì
![]()
![]() .
.
Câu 7:
Nhà thầy Hiếu trồng rất nhiều hoa ly để bán phục vụ tết. Trong ngày 29 tết âm lịch Thầy Hiếu bán hàng tại vườn từ lúc 6 giờ sáng đến 4 giờ chiều, cứ sau 1 tiếng thầy Hiếu lại đếm số cây hoa ly đã bán thì thấy số cây hoa ly bán được theo thời gian là (t: thời gian, đơn vị giờ). Giả sử là số cây bán được trong 1 giờ tại thời điểm t. Hỏi số cây hoa ly bán được nhiều nhất vào lúc mấy giờ?
 Xem đáp án
Xem đáp án
Chọn đáp án B.
Ta có
Xét hàm
![]() .
.
![]()
Bảng biến thiên:
Dựa vào bảng biến thiên:
Hàm số đạt giá trị lớn nhất tại nên số cây hoa ly bán được nhiều nhất vào lúc 11 giờ trưa.
Câu 8:
Một ô tô đang chuyển động đều với vận tốc 15m/s thì phía trước xuất hiện chướng ngại vật nên người lái xe đạp phanh gấp. Kể từ thời điểm đó, ô tô chuyển động chậm dần đều với gia tốc , . Biết ô tô chuyển động được 20m nữa thì dừng hẳn. Hỏi a thuộc khoảng nào dưới đây?
 Xem đáp án
Xem đáp án
Chọn đáp án C.
Ta có: .
Ô tô đang chuyển động đều với vận tốc 15 m/s.
.
Khi ô tô dừng hẳn thì .
Quãng đường ô tô gặp chướng ngại vật đến khi dừng hẳn là:
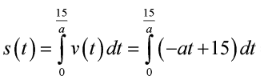
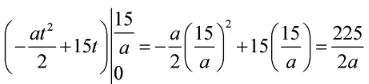 .
.
Ô tô đi được quãng đường 20m đến khi dừng hẳn nên
.
Vậy .
Câu 9:
Một người thợ nón muốn làm 100 cái nón sao cho mỗi chiếc nón có chu vi vành nón là 120 cm và khoảng cách từ đỉnh nón tới một điểm bất kì trên vành nón là 30 cm. Biết rằng để làm được 1 m2 mặt nón thì cần 120 lá nón đã qua sơ chế và giá 100 lá nón là 30.000đ. Hỏi người thợ cần bao nhiêu tiền để làm được 100 chiếc nón đó.
 Xem đáp án
Xem đáp án
Chọn đáp án A.
Gọi R là bán kính vành nón, ta có: (cm).
Giả thiết suy ra độ dài đường sinh là: cm.
Diện tích lá nón cần dùng là:
.
Vậy số là nón cần dùng là: lá nón.
Số tiền cần dùng là: đồng.
Câu 10:
Một bác thợ xây bơm nước vào bể chứa nước. Gọi h(t) là thể tích nước bơm được sau t giây. Cho và ban đầu bể không có nước. Sau 5 giây thì thể tích nước trong bể là 150m3. Sau 10 giây thì thể tích nước trong bể là 1100m3. Hỏi thể tích nước trong bể sau khi bơm được 20 giây là bao nhiêu?
 Xem đáp án
Xem đáp án
Chọn đáp án A
Ta có:
Ban đầu bể không có nước nên:
Sau 5 giây thể tích nước trong bể là 150m3.
Sau 10 giây thì thể tích nước trong bể là 1100m3
Giải hệ ta được .
Vậy thể tích nước trong bể sau khi bơm được 20 giây là
Câu 11:
Một người muốn có 2 tỉ tiền tiết kiệm sau 6 năm gửi ngân hàng bằng cách mỗi năm gửi vào ngân hàng số tiền bằng nhau với lãi suất ngân hàng là 8% một năm và lãi hàng tháng được nhập vào vốn. Hỏi số tiền mà người đó phải gửi vào ngân hàng hàng năm là bao nhiêu (với giả thiết lãi suất không thay đổi) và số tiền được làm tròn đến hàng nghìn đồng?
 Xem đáp án
Xem đáp án
Chọn đáp án A
Áp dụng công thức vay hoặc gửi tiền hàng kỳ:
A là số tiền vay hoặc gửi hàng kỳ; Sn là số tiền nợ hoặc nhận được.
r là lãi suất mỗi kỳ; n là kỳ hạn.
Số tiền hàng năm người đó phải gửi vào ngân hàng là:
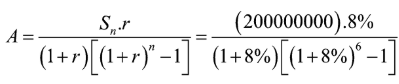
Câu 12:
Một cốc nước có dạng hình trụ chiều cao là 15 cm, đường kính đáy là 6 cm, lượng nước ban đầu trong cốc cao l0cm. Thả vào cốc nước 5 viên bi hình cầu có cùng đường kính là 2cm . Hỏi sau khi thả 5 viên bi, mực nước trong cốc cách miệng cốc bao nhiêu cm? (Kết quả làm tròn đến hàng phần trăm).
 Xem đáp án
Xem đáp án
Chọn đáp án C
Thể tích lượng nước có trong cốc là:
Tổng thể tích 5 viên bi được thả vào cốc là:
⇒ Tổng thể tích của nước và 5 viên bi là:
Vậy mực nước trong cốc cách miệng cốc
Câu 13:
Người ta trồng 3003 cây theo dạng một hình tam giác như sau: hàng thứ nhất trồng 1 cây, hàng thứ hai trồng 2 cây, hàng thứ ba trồng 3 cây, ..., cứ tiếp tục trồng như thế cho đến khi hết số cây. Số hàng cây được trồng là
 Xem đáp án
Xem đáp án
Chọn đáp án A
Gọi số cây ở hàng thứ n là un.
Ta có: và
Nhận xét dãy số là cấp số cộng có , công sai
Khi đó
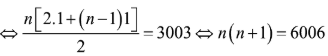
![]()
(vì )
Vậy số hàng cây được trồng là 77.
Câu 14:
Một người gửi tiết kiệm với lãi suất 8,4% /năm và lãi hàng tháng được nhập vào vốn. Hỏi sau bao nhiêu năm người đó có thu được gấp đôi số vốn ban đầu
 Xem đáp án
Xem đáp án
Chọn đáp án C
Áp dụng công thức lãi kép:
C là số tiền nhận được, A là số tiền gửi
R là lãi suất mỗi kì; n là kì hạn
Số tiền thu được gấp đôi
![]()
năm
Câu 15:
Trong không gian cho 2n điểm phân biệt (), trong đó không có ba điểm nào thẳng hàng và trong 2n điểm đó có đúng n điểm nằm cùng trên mặt phẳng và không có 4 điểm nào ngoài 4 điểm trong điểm này đồng phẳng. Tìm n sao cho từ 2n điểm đã cho tạo ra đúng 201 mặt phẳng phân biệt.
 Xem đáp án
Xem đáp án
Đáp án D
Câu 16:
Một vật chuyển động trong 3 giờ vận tốc v (km/h) phụ thuộc thời gian t (h) có đồ thị là một phần của đường parabol có đỉnh I (2;9) và trục đối xứng song song với trục tung như hình vẽ bên. Tính quãng đường s mà vật di chuyển được trong 3 giờ đó.
 Xem đáp án
Xem đáp án
Đáp án D
Câu 17:
Một vật chuyển động trong 4 giờ với vận tốc v (km/h) phụ thuộc thời gian t (h) có đồ thị là một phần của đường parabol có đỉnh I(1;1) và trục đôi xứng song song với trục tung như hình bên. Tính quãng đường s mà vật di chuyển được trong 4 giờ kể từ lúc xuất phát.
 Xem đáp án
Xem đáp án
Đáp án C
Câu 18:
Một giải thi đấu bóng đá quốc tế có 16 đội thi đấu vòng tròn 2 lượt tính điểm. (Hai đội bất kỳ đều thi đấu với nhau đúng 2 trận). Sau mỗi trận đấu, đội thắng được 3 điểm, đội thua 0 điểm; nếu hòa mỗi đội được 1 điểm. Sau giải đấu, ban tổ chức thống kê được 80 trận hòa. Hỏi tổng số điểm của tất cả các đội sau giải đấu bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án D
Câu 19:
Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc . Đi được 12 giây, người lái xe gặp chướng ngại vật và phanh gấp, ô tô tiếp tực chuyển động chậm dần đều với gia tốc . Tính quãng đường s(m) đi được của ô tô từ lúc bắt đầu chuyển động đến khi dừng hẳn?
 Xem đáp án
Xem đáp án
Đáp án A
Câu 20:
Anh Huy vay tiền ngân hàng 1 tỉ đồng theo phương thức trả góp (chịu lãi số tiền chưa trả) với lãi suất là 0,5%/tháng. Nếu cuối mỗi tháng bắt đầu từ tháng thứ nhất anh Huy trả 30 triệu đồng, thì sau bao nhiêu tháng anh Huy trả hết số nợ trên?
 Xem đáp án
Xem đáp án
Đáp án C
Câu 21:
Một ô tô đang chuyển động đều với vận tốc 20 m/s rồi hãm phanh chuyển động chậm dần đều với vận tốc , trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu hãm phanh. Tính quãng đường mà ô tô đi được trong 15 giây cuối cùng đến khi dừng hẳn.
 Xem đáp án
Xem đáp án
Đáp án C
Câu 22:
Thang đo Richte được Charles Francis đề xuất và sử dụng lần đầu tiên vào năm 1935 để sắp xếp các số đo độ chấn động của các cơn động đất với đơn vị Richte. Công thức tính độ chấn động như sau: , ML là độ chấn động, A là biên độ tối đa được đo bằng địa chấn kế và A0 là biên độ chuẩn. Hỏi theo thang độ Richte, cùng với một biên độ chuẩn thì biên độ tối đa của một trận động đất 7 độ Richte sẽ lớn gấp mấy lần biên độ của một trận động đất 5 độ Richte?
 Xem đáp án
Xem đáp án
Đáp án C
Câu 23:
Các loài cây xanh trong quá trình quang hợp sẽ nhận được một lượng cacbon 14 (một đồng vị của cacbon). Khi một bộ phận của cây bị chết thì hiện tượng quang hợp cũng ngưng và nó sẽ không nhận thêm cacbon 14 nữa. Lượng cacbon 14 của bộ phận đó sẽ phân hủy một cách chậm chạp, chuyển hóa thành nitơ 14. Biết rằng nếu gọi P(t) là phần trăm cacbon 14 còn lại trong bộ phận của một cây sinh trưởng từ t năm trước đây thì P(t) được tính theo công thức . Phân tích một mẫu gỗ từ một công trình kiến thức cổ, người ta thấy lượng cacbon 14 còn lại trong mẫu gỗ đó là 80%. Niên đại của công trình kiến trúc đó gần với số nào sau đây nhất? (Giả sử khoảng thời gian từ lúc thu hoạch gỗ cho đến khi xây dựng công trình đó là không đáng kể).
 Xem đáp án
Xem đáp án
Đáp án D
Câu 24:
Năm 2016 ở nước ta, số tiền để đổ đầy bình xăng cho một chiếc xe máy trung bình là 70 000 đồng. Giả sử tỉ lệ lạm phát hàng năm của Việt Nam trong 10 năm tới không đổi ở mức 5%. Tính số tiền để đổ đầy bình xăng cho một chiếc xe máy ở nước ta vào năm 2020.
 Xem đáp án
Xem đáp án
ĐÁP ÁN D
Câu 25:
Một dụng cụ đựng nước dạng hình nón (hình vẽ), có chiều cso 15 cm. Người ta đổ một lượng nước vào dụng cụ sao cho chiều cao của nước trong dụng cụ bằng chiều cao của dụng cụ. Hỏi nếu bịt kín miệng dụng cụ rồi lộn ngược dụng cụ lên thì chiều cao của nước gần bằng kết quả nào sau đây?
 Xem đáp án
Xem đáp án
ĐÁP ÁN B
Gọi R là bán kính đáy dụng cụ đó.
Lúc đầu: thể tích nước là:
Lúc sau: thể tích phần không gian trống bằng
Gọi h2 và R2 lần lượt là chiều cao và bán kính đáy của phần không gian trống.
Ta có:
Suy ra thể tích phần không gian trống bằng
Ta có:
Suy ra chiều cao nước là
Câu 26:
Cắt miếng bìa hình tam giác đều cạnh bằng 1 như hình bên và gấp theo các đường kẻ, sau đó dán các mép lại để được hình tứ diện đều. Tính thể tích V của hình tứ diện tạo thành.
 Xem đáp án
Xem đáp án
ĐÁP ÁN A
Câu 27:
Từ một hình tròn có tâm S, bán kính R, người ta tạo ra các hình nón theo hai cách sau đây:
-
Cách 1: Cắt bỏ 1/4 hình nón rồi ghép hai mép lại được hình nón N1.
-
Cách 2: Cắt bỏ 1/2 hình nón rồi ghép hai mép lại được hình nón N2.
Gọi V1, V2 lần lượt là thể tích của khối nón N1 và khối nón N2. Tính V1/V2
 Xem đáp án
Xem đáp án
ĐÁP ÁN D
Cách ghép 1: Xét hình nón N1 có độ dài đường sinh là
Do mặt xung quanh của hình nón N1 là hình nón ban đầu nên ta có hệ thức:
Suy ra
Cách ghép 2: Xét hình nón N2 có độ dài đường sinh là Tương tự, ta cũng tính được:
Do đó
Câu 28:
Một người gửi số tiền 1 triệu đồng vào một ngân hàng với lãi suất 7%/năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu (người ta gọi đó là lãi kép). Hỏi sau 4 năm người đó sẽ lĩnh bao nhiêu tiền (triệu đồng), nếu trong khoảng thời gian đó không rút tiền ra và lãi suất không thay đổi?
 Xem đáp án
Xem đáp án
ĐÁP ÁN A
Câu 29:
Một người gửi 10 triệu đồng vào ngân hàng. Hỏi nếu theo kì hạn 3 tháng với lãi suất 1,65% một quý thì sau hai năm người đó nhận được một số tiền (triệu đồng) là bao nhiêu?
 Xem đáp án
Xem đáp án
ĐÁP ÁN A
Câu 30:
Một bình đựng nước dạng hình nón (không có đáy), đựng đầy nước. Biết rằng chiều cao của bình gấp 3 lần bán kính đáy của nó, Người ta thả vào đó một khối trụ và đo được thể tích nước tràn ra ngoài là Biết rằng một mặt của khối trụ nằm trên mặt đáy của hình nón, các điểm trên đường tròn đáy còn lại đều thuộc các đường sinh của hình nón (như hình vẽ) và khối trụ có chiều cao bằng đường kính đáy của hình nón. Tính diện tích xung quanh của bình nước.
 Xem đáp án
Xem đáp án
ĐÁP ÁN B
Xét hình nón tròn xoay, ta có
Xét hình trụ tròn xoay, ta có
Do đồng dạng với nên
Suy ra thể tích khối trụ là:
Suy ra ![]()
![]()
Câu 31:
Biết rằng khối lượng chất phóng xạ tại thời điểm t là trong đó m0 là khối lượng chất phóng xạ ban đầu (tức tại thời điểm t = 0) và T là chu kì bán rã. Biết chi kì bán rã của một chất phóng xạ là 24 giờ (1 ngày đêm). Hỏi 100 gam chất đó sẽ còn lại bao nhiêu gam sau 4 ngày đêm?
 Xem đáp án
Xem đáp án
ĐÁP ÁN C
Câu 32:
Cho miếng tôn hình tròn tâm O bán kính R. Cắt bỏ một phần miếng tôn theo một hình quạt OAB và gò phần còn lại thành một hình nón đỉnh O hông đáy (OA trùng với OB). Gọi S, S’ lần lượt là diện tích của miếng tôn hình tròn ban đầu và diện tích của miếng tôn còn lại. Tìm tỉ số để thể tích khối nón lớn nhất.
 Xem đáp án
Xem đáp án
ĐÁP ÁN A
Gọi là bán kính đường tròn có độ dài AB, h > 0 là chiều cao của khối nón.
Ta có:
và
Khảo sát hàm số V theo biến ,
ta được thể tích lớn nhất khi
Do đó:
Câu 33:
Một khu rừng có trữ lượng gỗ là . Biết tốc độ sinh trưởng của các cây ở khu rừng đó là 4% mỗi năm. Hỏi sau 5 năm, khu rừng đó sẽ có số mét khối gỗ là bao nhiêu?
 Xem đáp án
Xem đáp án
ĐÁP ÁN D
Gọi là trữ lượng gỗ ban đầu, r% là tốc độ tăng trưởng hàng năm của rừng. Khi đó trữ lượng gỗ sau N năm là
Câu 34:
Một người gửi số tiền 1 triệu đồng vào một ngân hàng với lãi suất 7%/năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu (lãi kép). Sau 3 năm người đó sẽ lĩnh được số tiền là bao nhiêu (triệu đồng) (nếu trong khoảng thời gian này không rút tiền và lãi suất không thay đổi)?
 Xem đáp án
Xem đáp án
ĐÁP ÁN C
