15 câu hỏi trắc nghiệm thuộc DẠNG 4. SỰ BIẾN THIÊN CỦA HÀM SỐ

Câu 1:

Cho hàm số ${\rm{y}} = {\rm{f}}({\rm{x}})$ có đồ thị như Hình 1. Hàm số ${\rm{y}} = {\rm{f}}({\rm{x}})$ đồng biến trên khoảng

A. $( - 1;0).$

B. $(0;1).$

C. $(1;3).$

D. $( - 2; - 1).$

Xem đáp án

Chọn đáp án B

Câu 2:

Cho hàm số ${\rm{y}} = {\rm{f}}({\rm{x}})$ có đồ thị đạo hàm $y = {f^\prime }(x)$ như Hình 1. Hàm số ${\rm{y}} = {\rm{f}}({\rm{x}})$ đồng biến trên khoảng

A. $( - 2;0).$

B. $(0;2).$

C. $(1;3).$

D. $(3;4).$

Xem đáp án

Chọn đáp án C

Câu 3:

Cho hàm số ${\rm{y}} = {\rm{f}}({\rm{x}})$ có đồ thị như Hình 1. Hàm số ${\rm{y}} = {\rm{f}}({\rm{x}})$ nghịch biến trên khoảng

A. $( - 1;0).$

B. $(0;1).$

C. $(1;3).$

D. $( - 1;1).$

Xem đáp án

Chọn đáp án A

Câu 4:

Cho hàm số ${\rm{y}} = {\rm{f}}({\rm{x}})$ có đồ thị đạo hàm ${\rm{y}} = {{\rm{f}}^\prime }({\rm{x}})$ như Hình 1. Hàm số $y = f(x)$ nghịch biến trên khoảng

A. $( - 2; - 1).$

B. $(1;2).$

C. $(2;3).$

D. $( - 1;1).$

Xem đáp án

Chọn đáp án D

Câu 5:

Cho hàm số ${\rm{y}} = \frac{{{\rm{ax}} + {\rm{b}}}}{{{\rm{cx}} + {\rm{d}}}}({\rm{a}},{\rm{b}},{\rm{c}},{\rm{d}} \in \mathbb{R})$ có đồ thị như Hình 2. Phát biểu nào sau đây là đúng?

A. Hàm số đồng biến trên tập xác định.

B. Hàm số nghịch biến trên tập xác định.

C. Hàm số đồng biến trên từng khoảng xác định.

D. Hàm số nghịch biến trên từng khoảng xác định.

Xem đáp án

Chọn đáp án C

Câu 6:

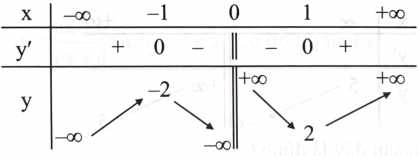
Cho hàm số ${\rm{y}} = \frac{{{\rm{a}}{{\rm{x}}^2} + {\rm{bx}} + {\rm{c}}}}{{{\rm{mx}} + {\rm{n}}}}({\rm{a}},{\rm{b}},{\rm{c}},{\rm{m}},{\rm{n}} \in \mathbb{R})$ có đồ thị như Hình 3. Phát biểu nào sau đây là đúng?

A. Hàm số đồng biến trên khoảng $( - 2; - 1)$ và nghịch biến trên khoảng $(2;3).$

B. Hàm số nghịch biến trên khoảng $( - 2; - 1)$ và nghịch biến trên khoảng $(2;3).$

C. Hàm số đồng biến trên khoảng $( - 2; - 1)$ và đồng biến trên khoảng $(2;3).$

D. Hàm số nghịch biến trên khoảng $( - 2; - 1)$ và đồng biến trên khoảng $(2;3).$

Xem đáp án

Chọn đáp án B

Câu 7:

Cho hàm số $y = f(x)$ có bảng biến thiên như sau:

$Cho hàm số $y = f(x)$ có bảng biến thiên như sau: 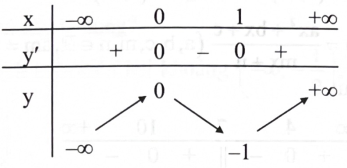Hàm số ${\rm{y}} = {\rm{f}}({\rm{x}})$ đồng biến trên khoảng A. $( - 1; + \infty ).$ B. $( - \infty ;1).$ C. $(0;1).$ D. $( - 3; - 2).$ (ảnh 1)$

Hàm số ${\rm{y}} = {\rm{f}}({\rm{x}})$ đồng biến trên khoảng

A. $( - 1; + \infty ).$

B. $( - \infty ;1).$

C. $(0;1).$

D. $( - 3; - 2).$

Xem đáp án

Chọn đáp án D

Câu 8:

Cho hàm số ${\rm{y}} = {\rm{f}}({\rm{x}})$ có bảng biến thiên như sau:

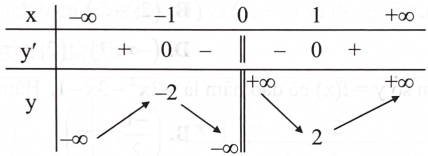
$Cho hàm số ${\rm{y}} = {\rm{f}}({\rm{x}})$ có bảng biến thiên như sau: Hàm số nghịch biến trên khoảng A. $( - 1;1).$ B. $( - \infty ; - 2).$ C. $(0;1).$ D. $(2; + \infty ).$ (ảnh 1)$

Hàm số nghịch biến trên khoảng

A. $( - 1;1).$

B. $( - \infty ; - 2).$

C. $(0;1).$

D. $(2; + \infty ).$

Xem đáp án

Chọn đáp án C

Câu 9:

Cho hàm số $y = f(x)$ có bảng biến thiên như sau:

$Cho hàm số $y = f(x)$ có bảng biến thiên như sau: 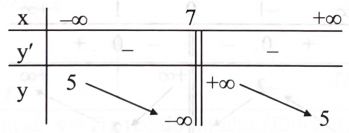Phát biểu nào sau đây là đúng? A. Hàm số đồng biến trên khoảng $(5;6)$ và nghịch biến trên khoảng $(8;9).$ B. Hàm số đồng biến trên khoảng $(5;6)$ và đồng biến trên khoảng $(8;9).$ C. Hàm số nghịch biến trên khoảng $(5;6)$ và đồng biến trên khoảng $(8;9).$ D. Hàm số nghịch biến trên khoảng $(5;6)$ và nghịch biến trên khoảng $(8;9).$ (ảnh 1)$

Phát biểu nào sau đây là đúng?

A. Hàm số đồng biến trên khoảng $(5;6)$ và nghịch biến trên khoảng $(8;9).$

B. Hàm số đồng biến trên khoảng $(5;6)$ và đồng biến trên khoảng $(8;9).$

C. Hàm số nghịch biến trên khoảng $(5;6)$ và đồng biến trên khoảng $(8;9).$

D. Hàm số nghịch biến trên khoảng $(5;6)$ và nghịch biến trên khoảng $(8;9).$

Xem đáp án

Chọn đáp án D

Câu 10:

Cho hàm số ${\rm{y}} = {\rm{f}}({\rm{x}})$ có đạo hàm trên $\mathbb{R}$ và có bảng xét dấu của đạo hàm như sau:

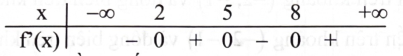
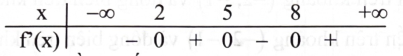
$Cho hàm số ${\rm{y}} = {\rm{f}}({\rm{x}})$ có đạo hàm trên $\mathbb{R}$ và có bảng xét dấu của đạo hàm như sau: Hàm số đã cho đồng biến trên khoảng A. $( - \infty ;2).$ B. $(5;8).$ C. $(3;4).$ D. $(5; + \infty ).$ (ảnh 1)$

Hàm số đã cho đồng biến trên khoảng

A. $( - \infty ;2).$

B. $(5;8).$

C. $(3;4).$

D. $(5; + \infty ).$

Xem đáp án

Chọn đáp án C

Câu 11:

Cho hàm số ${\rm{y}} = \frac{{{\rm{a}}{{\rm{x}}^2} + {\rm{bx}} + {\rm{c}}}}{{{\rm{mx}} + {\rm{n}}}}({\rm{a}},{\rm{b}},{\rm{c}},{\rm{m}},{\rm{n}} \in \mathbb{R},{\rm{am}} \ne 0)$ có bảng xét dấu của đạo hàm như sau:

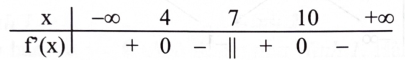
$Cho hàm số ${\rm{y}} = \frac{{{\rm{a}}{{\rm{x}}^2} + {\rm{bx}} + {\rm{c}}}}{{{\rm{mx}} + {\rm{n}}}}({\rm{a}},{\rm{b}},{\rm{c}},{\rm{m}},{\rm{n}} \in \mathbb{R},{\rm{am}} \ne 0)$ có bảng xét dấu của đạo hàm như sau: Hàm số đã cho nghịch biến trên khoảng A. $(11;12).$ B. $(7;10).$ C. $( - \infty ;7).$ D. $(4; + \infty ).$ (ảnh 1)$

Hàm số đã cho nghịch biến trên khoảng

A. $(11;12).$

B. $(7;10).$

C. $( - \infty ;7).$

D. $(4; + \infty ).$

Xem đáp án

Chọn đáp án A

Câu 12:

Cho hàm số ${\rm{y}} = {\rm{f}}({\rm{x}})$ có đạo hàm là ${{\rm{x}}^2} - 3{\rm{x}} + 2.$ Hàm số nghịch biến trên

A. $( - \infty ; - 1).$

B. $(2; + \infty ).$

C. $(1;2).$

D. $( - \infty ;1) \cup (2; + \infty ).$

Xem đáp án

Chọn đáp án C

Câu 13:

Cho hàm số $y = f(x)$ có đạo hàm là $ - 2{x^2} - 3x - 1.$ Hàm số đồng biến trên

A. $( - \infty ;1).$

B. $\left( {\frac{{ - 1}}{2}; + \infty } \right).$

C. $( - \infty ; - 1) \cup \left( {\frac{{ - 1}}{2}; + \infty } \right).$

D. $\left( { - 1;\frac{{ - 1}}{2}} \right).$

Xem đáp án

Chọn đáp án D

Câu 14:

Cho hàm số phù hợp với bảng biến thiên sau:

$Cho hàm số phù hợp với bảng biến thiên sau: Phát biểu nào sau đây là đúng? A. Hàm số đồng biến trên $( - \infty ; - 1)$ và $(1; + \infty )$, nghịch biến trên $( - 1;1).$ B. Hàm số đồng biến trên $( - \infty ; - 1)$ và $(1; + \infty )$, nghịch biến trên $( - 1;0)$ và $(0;1).$ C. Hàm số nghịch biến trên $( - \infty ; - 1)$ và $(1; + \infty )$, đồng biến trên $( - 1;1).$ D. Hàm số đồng biến trên $( - 1;0)$ và $(0;1)$, nghịch biến trên $( - \infty ; - 1)$ và $(1; + \infty ).$ (ảnh 1)$

Phát biểu nào sau đây là đúng?

A. Hàm số đồng biến trên $( - \infty ; - 1)$ và $(1; + \infty )$, nghịch biến trên $( - 1;1).$

B. Hàm số đồng biến trên $( - \infty ; - 1)$ và $(1; + \infty )$, nghịch biến trên $( - 1;0)$ và $(0;1).$

C. Hàm số nghịch biến trên $( - \infty ; - 1)$ và $(1; + \infty )$, đồng biến trên $( - 1;1).$

D. Hàm số đồng biến trên $( - 1;0)$ và $(0;1)$, nghịch biến trên $( - \infty ; - 1)$ và $(1; + \infty ).$

Xem đáp án

Chọn đáp án B

Câu 15:

Cho hàm số phù hợp với bảng biến thiên sau:

$Cho hàm số phù hợp với bảng biến thiên sau: Phát biểu nào sau đây là đúng? A. Hàm số nghịch biến trên hai khoảng $\left( { - \infty ; - \frac{1}{2}} \right);\left( {\frac{1}{2}; + \infty } \right)$ và đồng biến trên $\left( { - \frac{1}{2};\frac{1}{2}} \right).$ B. Hàm số nghịch biến trên hai khoảng $( - \infty ; - 1);(0; + \infty )$ và đồng biến trên $( - 1;0).$ C. Hàm số đồng biến trên hai khoảng $( - \infty ; - 1);(1; + \infty )$ và nghịch biến trên $( - 1;1).$ D. Hàm số nghịch biến trên $( - \infty ; - 1) \cup (1; + \infty )$ và đồng biến trên $( - 1;1).$ (ảnh 1)$

Phát biểu nào sau đây là đúng?

A. Hàm số nghịch biến trên hai khoảng $\left( { - \infty ; - \frac{1}{2}} \right);\left( {\frac{1}{2}; + \infty } \right)$ và đồng biến trên $\left( { - \frac{1}{2};\frac{1}{2}} \right).$

B. Hàm số nghịch biến trên hai khoảng $( - \infty ; - 1);(0; + \infty )$ và đồng biến trên $( - 1;0).$

C. Hàm số đồng biến trên hai khoảng $( - \infty ; - 1);(1; + \infty )$ và nghịch biến trên $( - 1;1).$

D. Hàm số nghịch biến trên $( - \infty ; - 1) \cup (1; + \infty )$ và đồng biến trên $( - 1;1).$

Xem đáp án

Chọn đáp án B