Trắc nghiệm tổng hợp ôn thi tốt nghiệp THPT môn Toán Chủ đề 6: Hình học và đo lường trong không gian có đáp án
CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN
-
69 lượt thi
-
14 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
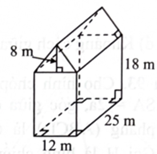
Hình bên là hình biểu diễn của vật thể ghép bởi khối hộp chữ nhật với ba kích thước 12 m, \(25\;{\rm{m}},18\;{\rm{m}}\) và khối lăng trụ tam giác có một chiều cao của mặt đáy là 8 m. Vật thể đó có thể tích bằng bao nhiêu \({{\rm{m}}^3}\) ?
Xem đáp án
Đáp số: 6600.
Khối đã cho được tạo thành từ khối lăng trụ và khối hộp chữ nhật.
Thể tích khối lăng trụ là: \(\frac{1}{2} \cdot 8 \cdot 12 \cdot 25 = 1200\left( {\;{{\rm{m}}^3}} \right).\)
Thể tích khối hộp chữ nhật là: \(18 \cdot 25 \cdot 12 = 5400\left( {\;{{\rm{m}}^3}} \right).\)
Thể tích của khối đã cho là: \(6600\;{{\rm{m}}^3}.\)
Câu 2:
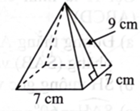
Hình bên là hình biểu diễn của khối chóp tứ giác đều có độ dài cạnh đáy bằng 7 cm và độ dài trung đoạn bằng 9 cm. Khối chóp đó có thể tích bằng bao nhiêu \({\rm{c}}{{\rm{m}}^3}\) (làm tròn kết quả đến hàng đơn vị )?
Xem đáp án
Đáp số: 135.
Độ dài đường cao khối chóp là \(\sqrt {{9^2} - {{\left( {\frac{7}{2}} \right)}^2}} = \frac{{5\sqrt {11} }}{2}.\)
Thể tích khối chóp là \(\frac{1}{3} \cdot \frac{{5\sqrt {11} }}{2} \cdot 7 \cdot 7 = \frac{{245\sqrt {11} }}{6}\left( {\;{\rm{c}}{{\rm{m}}^3}} \right).\)
Câu 3:
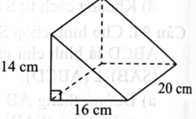
Hình bên là hình biểu diễn của khối vật thể có ba mặt hình chữ nhật và hai mặt tam giác vuông bằng nhau. Thể tích của khối vật thể là bao nhiêu \({\rm{c}}{{\rm{m}}^3}\) ?
Xem đáp án
Đáp số: 2240.
Khối đã cho là khối lăng trụ nên có thể tích \({\rm{V}} = \frac{1}{2} \cdot 14 \cdot 16 \cdot 20 = 2240\left( {\;{\rm{c}}{{\rm{m}}^3}} \right).\)
Câu 4:
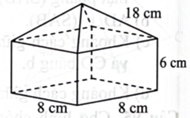
Hình bên là hình biểu diễn của khối vật thể có bốn mặt tam giác cân bằng nhau, bốn mặt hình chữ nhật và đáy là hình vuông. Thể tích của khối vật thể đó là bao nhiêu \({\rm{c}}{{\rm{m}}^3}\) (làm tròn kết quả đến hàng đơn vị)?
Xem đáp án
Đáp số: 749.
Khối đã cho được tạo thành từ khối chóp tứ giác đều và khối hộp chữ nhật.
Thể tích khối chóp tứ giác đều là \(\frac{1}{3} \cdot 8 \cdot 8 \cdot \sqrt {{{18}^2} - {{\left( {\frac{{8\sqrt 2 }}{2}} \right)}^2}} = \frac{{128\sqrt {73} }}{3}\left( {\;{\rm{c}}{{\rm{m}}^3}} \right).\)
Thể tích khối hộp chữ nhật là \(8 \cdot 8 \cdot 6 = 384\left( {\;{\rm{c}}{{\rm{m}}^3}} \right).\)
Thể tích khối đã cho là \(\frac{{128(9 + \sqrt {73} )}}{3}\left( {\;{\rm{c}}{{\rm{m}}^3}} \right).\)
Câu 5:
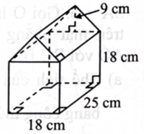
Hình bên là hình biểu diễn của khối vật thể có hai mặt tam giác cân bằng nhau, năm mặt hình chữ nhật và hai mặt hình vuông. Thể tích của khối vật thể đó là bao nhiêu \({\rm{d}}{{\rm{m}}^3}\) (làm tròn kết quả đến hàng phần mười)?
Xem đáp án
Đáp số: 10,1.
Khối đã cho được tạo thành từ khối lăng trụ và khối hộp chữ nhật.
Thể tích khối lăng trụ là \(\frac{1}{2} \cdot 9 \cdot 18 \cdot 25 = 2025\left( {\;{\rm{c}}{{\rm{m}}^3}} \right).\)
Thể tích khối hộp chữ nhật là \(18.25 \cdot 18 = 8100\left( {\;{\rm{c}}{{\rm{m}}^3}} \right).\)
Thể tích của khối đã cho là \(2025 + 8100 = 10125\left( {\;{\rm{c}}{{\rm{m}}^3}} \right).\)
Câu 6:
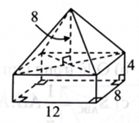
Hình bên là hình biểu diễn của khối vật thể được ghép bởi một hình hộp chữ nhật và một hình chóp tứ giác có hình chiếu của đỉnh trên mặt đáy là giao điểm của hai đường chéo. Thể tích của vật thể đó là bao nhiêu?
Xem đáp án
Đáp số: 640.
Khối đã cho được tạo thành từ khối chóp tứ giác và khối hộp chữ nhật.
Thể tích của khối chóp là \(\frac{1}{3} \cdot 8 \cdot 12 \cdot 8 = 256\) (đvtt).
Thể tích khối hộp chữ nhật là \(12 \cdot 8 \cdot 4 = 384\) (đvtt).
Thể tích của khối đã cho là \(256 + 384 = 640\) (đvtt).
Câu 7:
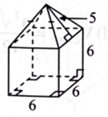
Hình bên là hình biểu diễn của khối vật thể được ghép bởi một khối lập phương và một khối chóp tứ giác đều. Diện tích toàn phần của hình đó là bao nhiêu?
Xem đáp án
Đáp số: 240.
Diện tích của năm mặt hình vuông là \(5 \cdot 6 \cdot 6 = 180\) (đvtt).
Diện tích của bốn mặt tam giác là \(4 \cdot \frac{1}{2} \cdot 5 \cdot 6 = 60\) (đvtt).
Diện tích toàn phần của khối đã cho là \(180 + 60 = 240\) (đvtt).
Câu 8:
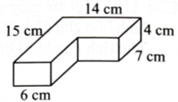
Hình bên là hình biểu diễn của khối vật thể có dạng chữ L được ghép bởi các khối hộp chữ nhật. Thể tích của vật thể đó bằng bao nhiêu \({\rm{c}}{{\rm{m}}^3}\) ?
Xem đáp án
Đáp số: 584.
Chia khối đã cho thành hai khối hộp chữ nhật có kích thước \(4\;{\rm{cm}},6\;{\rm{cm}},15\;{\rm{cm}}\) và \(4\;{\rm{cm}},7\;{\rm{cm}},8\;{\rm{cm}}.\)
Thể tích của khối đã cho là \(4 \cdot 6 \cdot 15 + 4 \cdot 8 \cdot 7 = 584\left( {\;{\rm{c}}{{\rm{m}}^3}} \right).\)
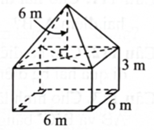
Câu 9:
Xem đáp án
Đáp số: 180.
Khối đã cho được tạo thành từ khối chóp tứ giác đều và khối hộp chữ nhật.
Thể tích của khối chóp là \(\frac{1}{3} \cdot 6 \cdot 6 \cdot 6 = 72\left( {\;{{\rm{m}}^3}} \right).\)
Thể tích khối hộp chữ nhật là \(6 \cdot 6 \cdot 3 = 108\left( {\;{{\rm{m}}^3}} \right).\)
Thể tích của khối đã cho là \(180\;{{\rm{m}}^3}.\)
Câu 10:
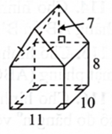
Thể tích của khối có hai mặt tam giác cân bằng nhau và bảy mặt hình chữ nhật với kích thước được cho như hình vẽ bên là bao nhiêu?
Xem đáp án
Đáp số: 1265.
Khối đã cho được tạo thành từ khối lăng trụ và khối hộp chữ nhật.
Thể tích khối lăng trụ là \(\frac{1}{2} \cdot 7 \cdot 11 \cdot 10 = 385\) (đvtt).
Thể tích khối hộp chữ nhật là \(11 \cdot 10 \cdot 8 = 880\) (đvtt).
Thể tích của khối đã cho là \(385 + 880 = 1265\) (đvtt).
Câu 11:
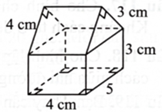
Hình bên là hình biểu diễn của khối vật thể được ghép bởi một hình hộp chữ nhật và một hình lăng trụ đứng có đáy là tam giác vuông với hai cạnh góc vuông dài \(3\;{\rm{cm}},4\;{\rm{cm}}.\) Thể tích của khối vật thể đó bằng bao nhiêu \({\rm{c}}{{\rm{m}}^3}\) ?
Xem đáp án
Đáp số: 84.
Khối đã cho được tạo thành từ khối lăng trụ và khối hộp chữ nhật.
Thể tích khối lăng trụ là \(\frac{1}{2} \cdot 3 \cdot 4 \cdot 4 = 24\left( {\;{\rm{c}}{{\rm{m}}^3}} \right).\)
Thể tích khối hộp chữ nhật là \(4 \cdot 5 \cdot 3 = 60\left( {\;{\rm{c}}{{\rm{m}}^3}} \right).\)
Thể tích của khối đã cho là \(84\;{\rm{c}}{{\rm{m}}^3}.\)
Câu 12:
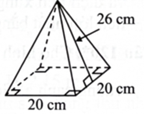
Thể tích của khối chóp tứ giác đều với các kích thước được cho như hình vẽ bên là bao nhiêu \({\rm{c}}{{\rm{m}}^3}\) ?
Xem đáp án
Đáp số: 3200.
Độ dài đường cao khối chóp tứ giác đều là \(\sqrt {{{26}^2} - {{10}^2}} = 24(\;{\rm{cm}}).\)
Thể tích khối chóp \(\frac{1}{3} \cdot 24 \cdot 20 \cdot 20 = 3200\left( {\;{\rm{c}}{{\rm{m}}^3}} \right).\)
Câu 13:
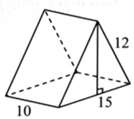
Hình bên là hình biểu diễn của khối vật thể có dạng lăng trụ đứng với chiều cao là 10, đáy là tam giác cân có cạnh đáy là 15 và cạnh bên là 12. Thể tích của khối vật thể đó là bao nhiêu (làm tròn kết quả đến hàng đơn vị)?
Xem đáp án
Đáp số: 703.
Khối đã cho là khối lăng trụ nên có thể tích là
\({\rm{V}} = \frac{1}{2}\sqrt {{{12}^2} - {{\left( {\frac{{15}}{2}} \right)}^2}} \cdot 15 \cdot 10 = \frac{{225\sqrt {39} }}{2} \approx 703\) (đvtt).
Câu 14:
Bạn Thuý cần gấp một hộp có dạng hình hộp đứng với chiều cao là 40 cm và diện tích xung quanh là \(2400\;{\rm{c}}{{\rm{m}}^2}.\) Khối hộp mà bạn Thuý cần gấp có thể tích lớn nhất bằng bao nhiêu \({\rm{c}}{{\rm{m}}^3}\) ?
Xem đáp án
Đáp số: 9000.
Đáy của hình hộp là hình bình hành. Gọi kích thước của hai đáy là \(x(\;{\rm{cm}})\) và \(y(\;{\rm{cm}}),{\rm{x}} > 0,{\rm{y}} > 0.\)
Diện tích xung quanh \((2x + 2y) \cdot 40 = 2400\), suy \({\rm{rax}} + {\rm{y}} = 30(\;{\rm{cm}}),{\rm{y}} = 30 - {\rm{x}}.\)
Diện tích của đáy không vượt quá xy.
Thể tích khối hộp không vượt quá
\(40{\rm{xy}} = 40{\rm{x}}(30 - {\rm{x}}) = - 40\left[ {{{({\rm{x}} - 15)}^2} - 225} \right]\) \( = - 40{(x + 15)^2} + 9000 \le 9000.\)