Đề số 11
-
6015 lượt thi
-
50 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):x + 2y - 2z + 2 =0 và mặt cầu tâm I(1;4;1) bán kính R tiếp xúc với (P). Bán kính R là:
 Xem đáp án
Xem đáp án
Đáp án B
Mặt cầu tâm I(1;4;1) tiếp xúc với mặt phẳng (P) nên .
Câu 4:
Cho số phức z = 5 +2i. Tìm phần thực và phần ảo của số phức z .
 Xem đáp án
Xem đáp án
Đáp án C
có phần thực bằng 5 và phần ảo bằng -2.
Câu 5:
Tìm a để hàm số liên tục tai điểm ?
 Xem đáp án
Xem đáp án
Đáp án B
Ta có:
Hàm số đã cho lien tục tại điểm x = 3 khi
Câu 6:
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;3;2); B(3;5;-4). Phương trình mặt phẳng trung trực của AB là:
 Xem đáp án
Xem đáp án
Đáp án D
và I(2;4;-1) là trung điểm của AB. Phương trình mặt phẳng trung trực của AB nhận véc tơ và đi qua điểm I là
Câu 7:
Chỉ ra mệnh đề sai trong các mệnh đề sau:
 Xem đáp án
Xem đáp án
Đáp án B
Hai đường thẳng vuông góc với nhau, mặt phẳng nào vuông góc với đường thẳng này thì song song hoặc chứa đường thẳng kia.
Câu 8:
Cho hai hình bình hành ABCD và ABEF nằm trong hai mặt phẳng phân biệt. Kết quả nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án A.
Do
Câu 9:
Cho hình chóp S.ABC có . Gọi I là hình chiếu vuông góc của S lên mp (ABC). Chọn khẳng định đúng trong các khẳng định sau?
 Xem đáp án
Xem đáp án
Đáp án B
Ta có: (cạnh huyền- cạnh góc vuông)
Suy ra IA = IB = IC hay I là tâm đường tròn ngoại tiếp tam giác ABC.
Đặt SA = SB = SC = x vuông tại A do
Do đó I là trung điểm của BC.
Câu 10:
Cho hình chóp S.ABCDcó đáy ABCD là hình vuông cạnh a, SA(ABCD), SA = . Gọi ![]() là góc giữa SC và mp (ABCD). Chọn khẳng định đúng trong các khẳng định sau?
là góc giữa SC và mp (ABCD). Chọn khẳng định đúng trong các khẳng định sau?
 Xem đáp án
Xem đáp án
Đáp án B
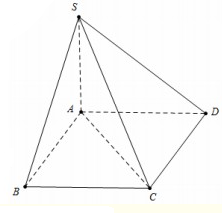
Ta có:
Do đó .
Câu 11:
Cho hàm số . Số tiệm cận của đồ thị hàm số là:
 Xem đáp án
Xem đáp án
Đáp án B
Đồ thị hàm số dạng có hai đường tiệm cận là: là TCN và là TCĐ. Vậy đồ thị hàm số có y = 2 là TCN và x = 1 là TCĐ.
Câu 12:
Cho hình chữ nhật ABCD có AB = 3AD. Quay hình chữ nhật ABCD lần lượt quanh AD và AB ta thu được hai hình trụ tròn xoay tương ứng có thể tích . Hỏi hệ thức nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án C
Quay hình chữ nhật ABCD quanh cạnh AD. Khi đó hình trụ có h = AD và r = AB nên .
Quay hình chữ nhật ABCD quanh canh AB. Khi đó hình trụ có h = AB và r = AD nên
nên
Câu 15:
Ba người cùng đi săn A, B, C độc lập với nhau cùng nổ súng bắn vào mục tiêu. Biết rằng xác suất bắn trúng mục tiêu của A, B, C tương ứng với 0,7; 0,6; 0,5. Tính xác suất để có ít nhất một xạ thủ bắn trúng?
 Xem đáp án
Xem đáp án
Đáp án C
Gọi là biến cố: Không một xạ thủ nào bắn trúng. Khi đó . Do A, B, C độc lập với nhau nên độc lập với nhau.
Suy ra .
Câu 16:
Cho a, b, c là các số thực dương, . Xét các mệnh đề sau:
(I)
(II)
(III)
Trong ba mệnh đề (I), (II), (III), tổng số mệnh đề đúng là?
 Xem đáp án
Xem đáp án
Đáp án C
Mệnh đề (I) đúng.
Mệnh đề (II) sai vì khi x > 0 nên điều kiện là chưa đủ.
Mệnh đề (III) sai vì
Số mệnh đề đúng là 1.
Câu 17:
Có 10 chiếc bút, 15 cái thước, 5 cái tẩy, các đồ vật này phân biệt. Chọn 1 đồ vật trong số các đồ vật trên. Hỏi có bao nhiêu cách chọn?
 Xem đáp án
Xem đáp án
Đáp án A
Chọn 1 đồ vật trong 30 đồ trên có cách chọn.
Câu 18:
Cho hàm số y = f(x). Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ có hệ số góc là:
 Xem đáp án
Xem đáp án
Đáp án D
PT tiếp tuyến của đồ thị hàm số tại điểm có hoành độ có hệ số góc .
Câu 20:
Cho x = log2017, y = ln2017. Hỏi quan hệ nào sau đây giữa x và y là đúng?
 Xem đáp án
Xem đáp án
Đáp án D
.
Câu 22:
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [1;4]. Tính hiệu M - m.
 Xem đáp án
Xem đáp án
Đáp án D
. So sánh các .
Vậy M - m = 10 - 6 = 4
Câu 23:
Cho số phức z thỏa mãn (2 - i)z = (2 + i)(1 - 3i). Gọi M là điểm biểu diễn của z. Khi đó tọa độ điểm M là.
 Xem đáp án
Xem đáp án
Đáp án B
Dùng CASIO rút gọn .
Câu 24:
Một hãng dược phẩm cần một số lọ đựng thuốc dạng hình trụ với dung tích . Tính bán kính đáy R của lọ để ít tốn nguyên liệu sản xuất lọ nhất.
 Xem đáp án
Xem đáp án
Đáp án A
Ta có:
Diện tích nguyên liệu cần dung là: . Lại có .
Dấu bằng xảy ra .
Câu 25:
Biết F(x) là nguyên hàm của hàm số và F(1) + 2F(2) = 40. Tính F(-1).
 Xem đáp án
Xem đáp án
Đáp án B
Ta có:
Lại có .
Do đó F(-1) = -3 + 10 = 7.
Câu 26:
Một khối nón có diện tích toàn phần bằng và diện tích xung quanh bằng . Tính thể tích V của khối nón đó.
 Xem đáp án
Xem đáp án
Đáp án B
Do đó .
Câu 27:
Đồ thị hàm số có bao nhiêu đường tiệm cận đứng?
 Xem đáp án
Xem đáp án
Đáp án C
Ta có:
Với đồ thị hàm số có 2 tiệm cận đứng.
Với đồ thị hàm số có 1 tiệm cận đứng.
Do đó đồ thị hàm số có 3 tiệm cận đứng.
Câu 28:
Cho số phức z có phần ảo âm, gọi . Khi đó khẳng định nào sau đây về w là đúng?
 Xem đáp án
Xem đáp án
Đáp án A
Đặt , vì z có phần ảo âm suy ra y < 0. Khi đó
Vậy w là một số thực.
Câu 30:
Cho số thực x lớn hơn 1 và ba số thực dương a, b, c khác 1 thỏa mãn điều kiện . Mệnh đề nào sau đây đúng ?
 Xem đáp án
Xem đáp án
Đáp án B
Ta có:
.
Câu 31:
Cho tích phân . Nếu đặt t = cos2x thì mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án B
Ta có:
Khi đó đặt . Đổi cận
Do đó .
Câu 32:
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị , tiệm cận ngang của (C) trục tung và đường thẳng x = a(a > 0). Tìm a để S = ln2017.
 Xem đáp án
Xem đáp án
Đáp án A
Tiệm cận ngang của (C) là y = 2. Khi đó
.
Câu 33:
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;-1;3) và hai đường thẳng, . Viết phương trình đường thẳng d đi qua A, vuông góc với đường thẳng và cắt đường thẳng .
 Xem đáp án
Xem đáp án
Đáp án C
Gọi . Cho
Khi đó .
Câu 35:
Trên mặt phẳng tọa độ Oxy, xét tam giác vuông OAB với A chạy trên trục hoành và có hoành độ dương; B chạy trên trục tung và có tung độ âm sao cho OA + OB = 1. Hỏi thể tích lớn nhất của vật thể tạo thành khi quay tam giác OAB quanh trục Oy bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án A
Khi quay quanh trục Oy, ta được hình nón có bán kính đáy r = OA và chiều cao h = OB. Theo bài ra, ta có OA + OB = r + h = 1 với (0 < r, h < 1)
Khi đó, thể tích khối nón là .
Ta có .
Tham khảo: Ta có thể đưa điểm B có tung độ âm về tung độ dương thì thể tích của khối nón không đổi.
Gọi suy ra phương trình đường thẳng .
Khi đó .
Ta có .
Câu 37:
Một hình lập phương cạnh bằng a nội tiếp khối cầu và ngoại tiếp khối cầu , gọi và lần lượt là thể tích của các khối và . Tính tỉ số .
 Xem đáp án
Xem đáp án
Đáp án D
Gọi khối lập phương cần xét ABCD.A'B'C'D' cạnh a.
Bán kính mặt cầu ngoại tiếp khối cầu là .
Bán kính mặt cầu ngoại tiếp khối cầu là
Vậy tỉ số .
Câu 38:
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, AA' = 2a. Biết thể tích hình cầu ngoại tiếp tứ diện ABCD' là . Tính thể tích V của hình hộp chữ nhật ABCD.A'B'C'D'.
 Xem đáp án
Xem đáp án
Đáp án B
Thể tích khối cầu ngoại tiếp tứ diện ABCD’ chính là thể tích khối cầu ngoại tiếp hình hộp chữ nhật ABCD.A’B’C’D’. Khi đó, bán kính khối cầu ngoại tiếp là .
Ta có .
Mặt khác .
Vậy thể tích của hình hộp chữ nhật ABCD.A'B'C'D' là .
Câu 39:
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1;0;0), B(0;3;0), C(0;0;2), D(1;3;-2). Hỏi có tất cả bao nhiêu mặt phẳng cách đều 5 điểm O, A, B, C, D (O là gốc tọa độ )?
 Xem đáp án
Xem đáp án
Đáp án A
Phương trình mặt phẳng (ABC) là mà .
Và ta thấy rằng và suy ra ABCD là hình bình hành.
Vậy O.ABCD là một hình chóp có đáy là hình bình hành, do đó có 5 mặt phẳng thỏa mãn yêu cầu gồm:
Mặt phẳng đi qua trung điểm của AC,BD và song song với (SAD) hoặc (SBC).
Mặt phẳng đi qua trung điểm cuả AD,BC đồng thời song song với (SAC) hoặc (SBD).
Mặt phẳng đi qua trungđiểm của OA,OB,OC,OD.
Câu 40:
Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số có đúng hai tiệm cận ngang?
 Xem đáp án
Xem đáp án
Đáp án D
Ta có
Đồ thị hàm số đã cho có hai đường TCN .
Câu 41:
Các giá trị của tham số m để phương trình có nghiệm thực khoảng (-1;0) là:
 Xem đáp án
Xem đáp án
Đáp án A
Phương trình .
Xét hàm số trên khoảng (-1;0) có .
Ta có .
Khi đó suy ra f(x) là hàm số đồng biến trên khoảng (-1;0)
Tính các giá trị suy ra và .
Nên để phương trình (*) có nghiệm .
Câu 42:
Cho đường tròn tâm O đường kính AB = 8. Trên AB lấy 2 điểm M, N đối xứng nhau qua O sao cho MN = 4. Qua M, N kẻ 2 dây cung PQ và EF cùng vuông góc với AB. Tính diện tích S phần giới hạn bới đường tròn và 2 dây cung PQ, EF (phần chứa điểm O ).
 Xem đáp án
Xem đáp án
Đáp án A
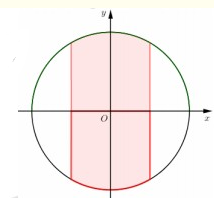 Chọn hệ trục tọa độ Oxy như hình vẽ với O là gốc tọa độ. Phương trình đường tròn tâm O, đường kính AB = 8 là .
Chọn hệ trục tọa độ Oxy như hình vẽ với O là gốc tọa độ. Phương trình đường tròn tâm O, đường kính AB = 8 là .
Diện tích hình phẳng cần tính gấp 2 lần diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số .
Khi đó .
Câu 43:
Gọi T là tập hợp các số phức z thỏa mãn và . Gọi lần lượt là các số phức có môđun nhỏ nhất và lớn nhất. Tìm số phức .
 Xem đáp án
Xem đáp án
Đáp án A
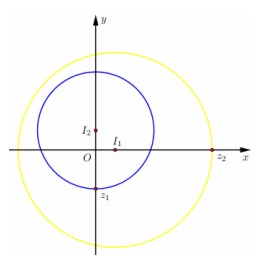
Đặt . Khi đó, ta có
Tập hợp các số phức nằm trong hoặc trên đường tròn
tâm bán kính .
Tập hợp các số phức nằm ngoài hoặc trên đường tròn tâm , bán kính .
Dựa vào hình vẽ, ta thấy rằng .
Câu 44:
Cho hàm số y = f(x) liên tục trên và hàm số có đồ thị trên đoạn [0;2] như hình vẽ bên. Biết diện tích miền được tô màu là , tính tích phân .
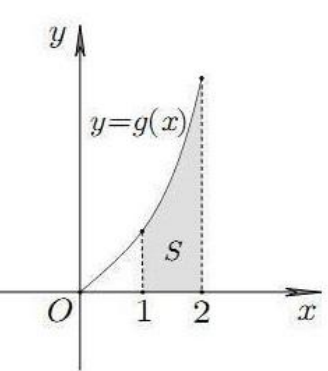
 Xem đáp án
Xem đáp án
Đáp án C
.
Câu 45:
Một sân chơi cho trẻ em hình chữ nhật có chiều dài 100m và chiều rộng là 60m người ta làm một con đường nằm trong sân (như hình vẽ). Biết rằng viền ngoài và viền trong của con đường là hai đường Elip, Elip của đường viền ngoài có trục lớn và trục bé lần lượt song song với các cạnh hình chữ nhật và chiều rộng của mặt đường là 2m. Kinh phí của mỗi làm đường 600.000đồng. Tính tổng số tiền làm con đường đó. (Số tiền được làm tròn đến hàng nghìn).
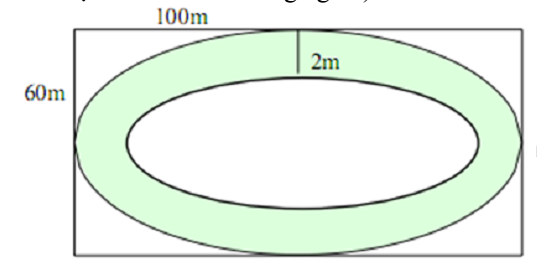
 Xem đáp án
Xem đáp án
Đáp án D
Đặt hệ trục tọa độ với tâm O là giao điểm 2 đường chéo hình chữ nhật và Ox, Oy song song với cạnh chiều dài và chiều rộng.
Diện tích mặt đường là diện tích phần mặt phẳng giới hạn bởi 2 elip và .
Số tiền là đường là:
Câu 46:
Trong không gian với hệ tọa độ Oxyz cho ba điểm A(0;1;1), B(3;0;-1), C(0;21;-19) và mặt cầu . M(a;b;c) là điểm thuộc mặt cầu (S) sao cho biểu thức đạt giá trị nhỏ nhất. Tính tổng a + b + c.
 Xem đáp án
Xem đáp án
Đáp án D
Gọi điểm sao cho suy ra điểm I(1;4;-3)
Xét mặt cầu có tâm E(1;1;1) và bán kính R = 1.
Suy ra . Ta có
.
Để tổng T đạt giá trị nhỏ nhất khi và chỉ khi MI nhỏ nhất vì tổng không đổi. Suy ra M, E, I thẳng hàng mà IE = 5 và EM = 1 nên .
Lại có và suy ra
Câu 47:
Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng 1, SA vuông góc với đáy, góc giữa mặt bên (SBC) và đáy bằng 60. Diện tích mặt cầu ngoại tiếp hình chóp S.ABC bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án C
Gọi M là trung điểm BC.
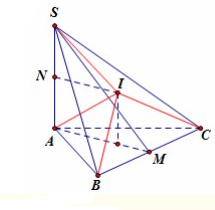
Dễ dàng chứng minh
. Đây là khối chóp có cạnh bên
vuông góc đáy nên bán kính mặt cầu ngoại tiếp được tính là: .
Câu 49:
Cho hình phẳng (H) giới hạn bởi các đường . Gọi là thể tích khối tròn xoay thu được khi quay hình (H) quanh trục Ox. Biết rằng , hãy chọn khẳng định đúng?
 Xem đáp án
Xem đáp án
Đáp án C
Thể tích khối tròn xoay cần tính là .
Đặt suy ra .
Mặt khác suy ra
Câu 50:
Một khối đá có hình một khối cầu có bán kính R, người thợ thủ công mỹ nghệ cần cắt và gọt viên đá đó thành một viên đá cảnh có hình dạng là một khối trụ. Tính thể tích lớn nhất có thể của viên đá cảnh sau khi đã hoàn thiện.
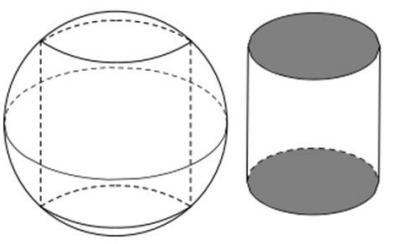
 Xem đáp án
Xem đáp án
Đáp án B
Gọi h và r (0 < h,r < 2R) lần lượt là chiều cao và bán kính mặt đáy của viên đá cảnh hình trụ và áp dụng bất đẳng thức với 3 số x,y,z > 0 là:
Thể tích viên đá là:
