50 câu hỏi trắc nghiệm thuộc Đề số 7

Câu 1:

Cho hình lập phương cạnh 4cm. Trong khối lập phương là khối cầu tiếp xúc với các mặt của hình lập phương. Tính thể tích phần còn lại của khối lập phương.

A. $64 - \frac{64 \sqrt{2}}{3} π {cm}^{3}$

B. $64 - 32 \sqrt{3} π {cm}^{3}$

C. $64 - \frac{32}{3} π {cm}^{3}$

D. $64 - \frac{256}{81} π {cm}^{3}$

Xem đáp án

Đáp án C.

Khối cầu nội tiếp hình lập phương cạnh a có bán kính là $\frac{a}{2} \overset{G T}{\to} R = 2 .$

$V = V_{L P} - V_{C} = 4^{3} - \frac{4}{3} π 2^{3} = 64 - \frac{32 π}{3} .$

Câu 2:

Tìm nguyên hàm của hàm số $f (x) = \cos^{2} x$ ta được

A. $\int f (x) d x = \frac{x}{2} - \frac{\cos 2 x}{4} + C$

B. $\int f (x) d x = \frac{x}{2} - \frac{\sin 2 x}{4} + C$

C. $\int f (x) d x = \frac{x}{2} + \frac{\cos 2 x}{4} + C$

D. $\int f (x) d x = \frac{x}{2} + \frac{\sin 2 x}{4} + C$

Xem đáp án

Đáp án D.

$\int \cos^{2} x d x = \frac{1}{2} \int (1 + \cos 2 x) d x = \frac{x}{2} + \frac{\sin 2 x}{4} + C$

Câu 3:

Cho phương trình $\cos 2 (x + \frac{π}{3}) + 4 \cos (\frac{π}{6} - x) = \frac{5}{2}$ . Khi đặt $t = \cos (\frac{π}{6} - x)$ , phương trình đã cho trở thành phương trình nào dưới đây?

A. $4 t^{2} - 8 t + 3 = 0$

B. $4 t^{2} - 8 t - 3 = 0$

C. $4 t^{2} + 8 t - 5 = 0$

D. $4 t^{2} - 8 t + 5 = 0$

Xem đáp án

Đáp án A.

Ta có $\cos 2 (x + \frac{π}{3}) = \cos (2 x + \frac{2 π}{3}) = - \cos (\frac{π}{3} - 2 x) = - \cos 2 (x - \frac{π}{6}) = 1 - 2 \cos^{2} (x - \frac{π}{6}) = 1 - 2 t^{2}$

Phương trình tương đương: $1 - 2 t^{2} + 4 t = \frac{5}{2} \Leftrightarrow 4 t^{2} - 8 t + 3 = 0 .$

Câu 4:

Trong các hàm số dưới đây, hàm số nào không nghịch biến trên $ℝ$ ?

A. $y = - x^{3} + 2 x^{2} - 7 x$

B. $y = - 4 x + \cos x$

C. $y = - \frac{1}{x^{2} + 1}$

D. $y = {(\frac{\sqrt{2}}{\sqrt{2} + \sqrt{3}})}^{x}$

Xem đáp án

Đáp án C.

Xét $y = - \frac{1}{x^{2} + 1} \Rightarrow y' = \frac{2 x}{{(x^{2} + 1)}^{2}} \to y' = 0 \Leftrightarrow x = 0$

Hàm số này đồng biến trên $(0; + \infty)$ và nghịch biến trên $(- \infty; 0)$

Câu 5:

Cho đường thẳng $d : \frac{x + 1}{2} = \frac{y - 4}{- 2} = \frac{z + 2}{1}$ và mặt phẳng $(P) : x + 2 y - z - 6 = 0$ cắt nhau tại I. Gọi M là điểm thuộc d sao cho IM = 6. Tính khoảng cách từ điểm M đến mặt phẳng (P).

A. $\sqrt{6}$

B. $2 \sqrt{6}$

C. $\sqrt{30}$

D. $\frac{\sqrt{6}}{2}$

Xem đáp án

Đáp án A.

I(2t - 1;-2t + 4;t - 2). Do $I = d \cap (P)$ nên $(2 t - 1) + 2 (- 2 t + 4) - (t - 2) - 6 = 0 \Leftrightarrow t = 1 .$

Do đó I(1;2;-1). Mặt khác $M (2 m - 1; - 2 m + 4; m - 2) \in \to I M = (2 m - 2; - 2 m + 2; m - 1) .$

Giả thiết $I M = 6 \Leftrightarrow I M^{2} = 36 \Leftrightarrow 9 {(m - 1)}^{2} = 36 \Leftrightarrow [\begin{array}{l} m - 1 = 2 \\ m - 1 = - 2 \end{array} \Leftrightarrow [\begin{array}{l} m = 3 \\ m = - 1 \end{array}$ (Thử 1 giá trị m).

Suy ra $d (M; (P)) = \sqrt{6} .$

Câu 6:

Kí hiệu $z_{0}$ là nghiệm phức có phần thực âm và phần ảo dương của phương trình $z^{2} + 2 z + 10 = 0$ . Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn số phức $w = i^{2017} z_{0}$ ?

A. M(3;-1)

B. M(3;1)

C. M(-3;1)

D. M(-3;-1)

Xem đáp án

Đáp án D.

Ta có $z^{2} + 2 x + 10 = 0 \Leftrightarrow z = - 1 \pm 3 i \Rightarrow z_{0} = - 1 + 3 i \Rightarrow w = i^{2017} z_{0} = i z_{0} = - 3 - i .$

Câu 7:

Tính tổng S các nghiệm của phương trình $(2 \cos 2 x + 5) (\sin^{4} x - \cos^{4} x) + 3 = 0$ trong khoảng $(0; 2 π)$ .

A. $S = \frac{11 π}{6}$

B. $S = 4 π$

C. $S = 5 π$

D. $S = \frac{7 π}{6}$

Xem đáp án

Đáp án B.

PT $\Leftrightarrow (2 \cos 2 x + 5) (\sin^{2} x - \cos^{2} x) (\sin^{2} x + \cos^{2} x) + 3 = - (2 \cos 2 x + 5) \cos 2 x + 3 = 0$

$\Leftrightarrow 2 \cos^{2} 2 x + 5 \cos 2 x - 3 = 0 \Leftrightarrow [\begin{array}{l} \cos 2 x = - 3 (!) \\ \cos 2 x = \frac{1}{2} \end{array} \Leftrightarrow 2 x = \pm \frac{π}{3} + k 2 π$

$\Leftrightarrow x = \pm \frac{π}{3} + k π \in (0; 2 π) \Leftrightarrow x \in \{\frac{π}{6}; \frac{5 π}{6}; \frac{7 π}{6}; \frac{11 π}{6}\} \Rightarrow S = 4 π .$

Câu 8:

Biết rằng phương trình ${(x - 2)}^{\log_{2} [4 (x - 2)]} = 4 . {(x - 2)}^{3}$ có hai nghiệm $x_{1}, x_{2} (x_{1} < x_{2})$ . Tính $2 x_{1} - x_{2}$ .

A. 1

B. 3

C. -5

D. -1

Xem đáp án

Đáp án D.

ĐK: x > 2.

TH1: Ta thấy x = 3 không phải là nghiệm của PT.

TH2: Với $x \neq 3$ logarit cơ số x - 2 cả 2 vế ta được $\log_{2} [4 (x - 2)] = \log_{(x - 2)} 4 + 3$

$\Leftrightarrow 2 + \log_{2} (x - 2) = 2 \log_{x - 2} 2 + 3 \Leftrightarrow \log_{2} (x - 2) - 2 \log_{x - 2} 2 - 1 = 0$

Đặt $t = \log_{2} (x - 2) \Rightarrow t - \frac{2}{t} - 1 = 0 \Leftrightarrow t^{2} - t - 2 = 0 \Leftrightarrow [\begin{array}{l} t = - 1 \\ t = 2 \end{array}$

Với $t = - 1 \Rightarrow x = \frac{5}{2}$ ; với $t = 2 \Rightarrow x = 6 \Rightarrow [\begin{array}{l} x_{1} = \frac{5}{2} \\ x_{2} = 6 \end{array} \Rightarrow 2 x_{1} - x_{2} = - 1 .$

Câu 9:

Viết phương trình mặt phẳng vuông góc với mặt phẳng $(α) : 2 x - 3 y + z - 2 = 0$ và chứa đường thẳng $d : \frac{x}{- 1} = \frac{y + 1}{2} = \frac{z - 2}{- 1} .$

A. x - y + z - 3 = 0

B. 2x + y - z + 3 = 0

C. x + y + z - 1 = 0

D. 3x + y - z + 3 = 0

Xem đáp án

Đáp án C.

Ta có: $n_{α} = (2; - 3; 1)$ ; d qua M(0;-1;2) và $u_{d} = (- 1; 2; - 1)$

Khi đó mặt phẳng (P) cần tìm có $n_{p} = [n_{α}; u_{d}] = (1; 1; 1)$ và đi qua M(0;-1;2) có phương trình là x + y + z - 1 = 0.

Câu 10:

Tìm số phức liên hợp của số phức $z = (1 - i) (3 + 2 i)$ .

A. $z = 1 + i$

B. $z = 5 + i$

C. $z = 5 - i$

D. $z = 1 - i$

Xem đáp án

Đáp án B.

Ta có: $z = (1 - i) (3 + 2 i) = 5 - i \Rightarrow z = 5 + i$ .

Câu 11:

Tìm số nghiệm thuộc $[- \frac{3 π}{2}; - π)$ của phương trình $\sqrt{3} \sin x = \cos (\frac{3 π}{2} - 2 x)$ .

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Đáp án B.

PT $\Leftrightarrow \sqrt{3} \sin x = - \cos (\frac{π}{2} - 2 x) = - \sin 2 x = - 2 \sin x \cos x \Leftrightarrow \sin x (2 \cos + \sqrt{3}) = 0$

$\Leftrightarrow [\begin{array}{l} \sin x = 0 \\ \cos = - \frac{\sqrt{3}}{2} \end{array} \Leftrightarrow \{\begin{cases} x = k π \\ x = \pm \frac{5 π}{6} + k 2 π \end{cases}$

Với $x \in [- \frac{3 π}{2}; π) \Rightarrow x = \frac{- 7 π}{6}$ .

Câu 12:

Cho hàm số $y = a x^{4} + b x^{2} + c$ có đồ thị là hình vẽ dưới đây. Mệnh đề nào sau đây là đúng?

A. $a > 0, b < 0, c > 0, b^{2} - 4 a c > 0$

B. $a > 0, b < 0, c > 0, b^{2} - 8 a c > 0$

C. $a > 0, b < 0, c > 0, b^{2} - 4 a c < 0$

D. $a > 0, b < 0, c > 0, b^{2} - 8 a c < 0$

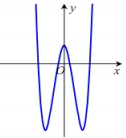
Xem đáp án

Đáp án A.

Ta có: $\lim_{x \to + \infty} y = + \infty$ nên a > 0; đồ thị hàm số có 3 cực trị nên $a b < 0 \Rightarrow b < 0;$

Đồ thị hàm số cắt Oy tại điểm $(0; c) \Rightarrow c > 0$ .

Với $x^{2} = \frac{- b}{2 a}$ thế vào ta được $y_{C T} = a . \frac{b^{2}}{4 a^{2}} - \frac{b^{2}}{2 a} + c < 0 \Leftrightarrow \frac{- b^{2}}{4 a} + c < 0 \Leftrightarrow b^{2} - 4 a c > 0$ .

Câu 13:

Cho khối lăng trụ ABC.A’B’C’ có đáy làm tam giác vuông tại B, AB = a, BC = 2a và có thể tích bằng $2 a^{2}$ . Tính khoảng cách giữa hai đáy lăng trụ.

A. 6a

B. a

C. 2a

D. 3a

Xem đáp án

Đáp án C.

Ta có: $S_{A B C} = \frac{1}{2} A B . B C = a^{2} \Rightarrow h = \frac{V}{S} = 2 a$ .

Câu 14:

Cho đường thẳng $d : \frac{x - 1}{- 1} = \frac{y}{2} = \frac{z - 3}{4}$ và mặt phẳng (P): 2x - y + z - 5 = 0. Xét vị trí tương đối của (d) và (P).

A. d nằm trên (P)

B. d song song với (P)

C. d cắt và vuông góc với (P)

D. d vuông góc với (P)

Xem đáp án

Đáp án A.

Ta có: $u_{d} . n_{p} = - 2 - 2 + 4 = 0$ nên $[\begin{array}{l} d / / (P) \\ d \subset (P) \end{array}$

Mặt khác điểm A(1;0;3) và A(1;0;3) $\in (P)$ nên d nằm trên (P).

Câu 15:

Biết $\int_{a}^{b} f (x) d x = 10, \int_{a}^{b} g (x) d x = 5 .$ Tính $I = \int_{a}^{b} (3 f (x) - 5 g (x)) d x$ .

A. I = -5

B. I = 15

C. I = 5

D. I = 10

Xem đáp án

Đáp án C.

Ta có: $I = \int_{a}^{b} (3 f (x) - 5 g (x)) d x = 3 \int_{a}^{b} f (x) d x - 5 \int_{a}^{b} g (x) d x = 3.10 - 5.5 = 5$ .

Câu 16:

Cho hình chóp đều SABC có AB = 1cm, SA = 2cm. Tính diện tích xung quanh $S_{x q}$ của hình nón ngoại tiếp hình chóp SABC.

A. $S_{x q} = \frac{3 \sqrt{3}}{4} π ({cm}^{2})$

B. $S_{x q} = \frac{2 \sqrt{3}}{3} π ({cm}^{2})$

C. $S_{x q} = \frac{\sqrt{3}}{2} π ({cm}^{2})$

D. $S_{x q} = 2 π ({cm}^{2})$

Xem đáp án

Đáp án B.

Bán kính mặt đáy là $R = \frac{2}{3} . \frac{A B \sqrt{3}}{2} = \frac{\sqrt{3}}{3} \Rightarrow S_{x q} = πRl = π . \frac{\sqrt{3}}{3} . 2 = \frac{2 π \sqrt{3}}{3}$ .

Câu 17:

Cho số phức $z = a + b i (a, b \in ℝ)$ thỏa điều kiện $(2 - 3 i) z - 7 i . z = 22 - 20 i$ . Tính a+b

A. 3

B. -4

C. -6

D. 2

Xem đáp án

Đáp án B.

Ta có $(2 - 3 i) (a + b i) - 7 i (a - b i) = 22 - 20 i \Leftrightarrow (2 a - 4 b) + (2 b - 10 a) i = 22 - 20 i$

$\Rightarrow \{\begin{cases} 2 a - 4 b = 22 \\ 2 b - 10 a = - 20 \end{cases} \Leftrightarrow \{\begin{cases} a = 1 \\ b = - 5 \end{cases} \Rightarrow a + b = - 4$ .

Câu 18:

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng $d_{1} : \frac{x - 3}{2} = \frac{y - 1}{- 1} = \frac{z - 2}{1}$ và $d_{2} : \frac{x - 5}{- 2} = \frac{y}{1} = \frac{z - 3}{- 1}$ . Xét vị trí tương đối của $d_{1}$ và $d_{2}$

A. $d_{1}$ và $d_{2}$ trùng nhau

B. $d_{1}$ và $d_{2}$ song song

C. $d_{1}$ và $d_{2}$ cắt nhau

D. $d_{2}$ và $d_{2}$ chéo nhau.

Xem đáp án

Đáp án A.

Ta có $u_{1} = (2; - 1; 1)$ và $u_{2} = (- 2; 1; - 1)$ suy ra $\vec{u_{1}} = - \vec{u_{2}}$ .

Mặt khác $M (3; 1; 2) \in d_{1}$ và $M \in d_{2}$ suy ra $d_{1}$ và $d_{2}$ trùng nhau.

Câu 19:

Một kỹ sư được nhận lương khởi điểm là 8.000.000 đồng/tháng. Cứ sau hai năm lương mỗi tháng của kỹ sư đó được tăng thêm 10% so với mức lương hiện tại. Tính tổng số tiền T (đồng) kỹ sư đó nhận được sau 6 năm làm việc.

A. 633.600.000

B. 635.520.000

C. 696.960.000

D. 766.656.000

Xem đáp án

Đáp án B.

Gọi x là số tiền kỹ sư nhận được sau 1 năm.

Vậy sau 6 năm, tổng số tiền nhận được là T = 2x $(1 + 1, 1 + 1, 1^{2}) = 6, 62 x$

Với x = 8.12 = 96 triệu đồng suy ra T = 6.62.96 = 635,52 triệu đồng.

Câu 20:

Cho $f (x) = \sqrt{1 + 3 x} - \sqrt[3]{1 + 2 x}, g (x) = \sin x$ . Tính giá trị của $\frac{f' (0)}{g' (0)}$ .

A. $\frac{5}{6}$

B. $- \frac{5}{6}$

C. 0

D. 1

Xem đáp án

Đáp án A.

Ta có $\{\begin{cases} f' (x) = \frac{3}{2 \sqrt{1 + 3 x}} \\ g' (x) = c o s x \end{cases} \Rightarrow \frac{f' (0)}{g' (0)} = \frac{5}{6} .$

Câu 21:

Tìm tất cả các giá trị của tham số thực m sao cho hàm số $f (x) = \{\begin{cases} 2 \sqrt{x} - m k h i x \geq 0 \\ m x + 2 k h i x < 0 \end{cases}$ liên tục trên $ℝ$ .

A. m = 2

B. m = $\pm 2$

C. m = -2

D. m = 0

Xem đáp án

Đáp án C.

Dễ thấy hàm số liên tục trên các khoảng $(0; + \infty)$ và $(- \infty; 0)$ . Ta có:

$\{\begin{cases} f (0) = - m \\ \lim_{x \to 0^{+}} f (x) = - m \\ \lim_{x \to 0^{-}} f (x) = 2 \end{cases}$ . Để hàm số liên tục tại x = 0 thì $\lim_{x \to 0^{+}} f (x) = \lim_{x \to 0^{-}} f (x) = f (0) \Leftrightarrow m = - 2$ .

Câu 22:

Số tiếp tuyến của đồ thị hàm số $y = \frac{x^{3}}{x - 2} - 27$ song song với trục hoành là

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Đáp án B.

Ta có $y' = \frac{3 x^{2} (x - 2) - x^{3}}{{(x - 2)}^{2}} = \frac{2 x^{2} (x - 3)}{{(x - 2)}^{2}}$ .

Do tiếp tuyến song song với trục hoành $\Rightarrow y' = 0 \Leftrightarrow [\begin{array}{l} x = 0 \Rightarrow y = - 27 \\ x = 3 \Rightarrow y = 0 \end{array}$

Với x = 3,y = 27 $\Rightarrow$ PTTT là: y = 0 $\equiv O x$ (loại)

Với x = 0, y = -27 $\Rightarrow$ PTTT là: y = -27.

Vậy có 1 tiếp tuyến thỏa mãn.

Câu 23:

Trong mặt phẳng với hệ tọa độ Oxyz, cho $∆ A B C$ có A(2;4), B(5;1), C(-1;-2). Phép tịnh tiến $T_{\vec{B C}}$ biến $∆ A B C$ thành $∆ A' B' C'$ Tìm tọa độ trọng tâm của $∆ A' B' C'$

A. (-4;2)

B. (4;2)

C. (4;-2)

D. (-4;-2)

Xem đáp án

Đáp án D.

Tọa độ trọng tâm tam giác ABC là G(2;1). Trọng tâm của tâm giác A’B’C’ là G’

Ta có $\vec{B C} = (- 6; - 3)$ , vì $T_{\vec{B C}} (∆ A B C) = ∆ A' B' C' \Rightarrow T_{\vec{B C}} (G) = G' (- 4; - 2)$ .

Câu 24:

Cho $\int_{1}^{3} f (x) d x = - 5, \int_{1}^{3} [f (x) - 2 g (x)] d x = 9$ . Tính $I = \int_{1}^{3} g (x) d x$ .

A. I = 14

B. I = -14

C. I = 7

D. I = -7

Xem đáp án

Đáp án D.

Ta có $\int_{1}^{3} [f (x) - 2 g (x)] d x = \int_{1}^{3} f (x) d x - 2 . \int_{1}^{3} g (x) d x = 9 \Rightarrow \int_{1}^{3} g (x) d x = \frac{- 5 - 9}{2} = - 7$ .

Câu 25:

Biết $\int_{\frac{π}{4}}^{\frac{π}{2}} \frac{x}{\sin^{2} x} d x = m π + nln 2 (m, n \in ℝ)$ , hãy tính giá trị của biểu thức P = 2m + n.

A. P = 1

B. P = 0,75

C. P = 0,25

D. P = 0

Xem đáp án

Đáp án A.

Đặt $\{\begin{array}{l} u = x \\ d v = \frac{d x}{\sin^{2} x} \end{array} \Leftrightarrow \{\begin{cases} d u = d v \\ v = - c o t x \end{cases}$ , khi đó $\int_{\frac{π}{4}}^{\frac{π}{2}} \frac{x}{\sin^{2} x} d x = {(- x . c o t x)}_{\frac{π}{4}}^{\frac{π}{2}} + \int_{\frac{π}{4}}^{\frac{π}{2}} c o t x d x$ .

Xét tích phân $\int_{\frac{π}{4}}^{\frac{π}{2}} c o t x d x = \int_{\frac{π}{4}}^{\frac{π}{2}} \frac{\cos x}{\sin x} d x = \int_{\frac{π}{4}}^{\frac{π}{2}} \frac{d (\sin x)}{\sin x} = {\ln (\sin x)}_{\frac{π}{4}}^{\frac{π}{2}} = - \ln \frac{\sqrt{2}}{2} .$

Vậy $I = {(- x . c o t x)}_{\frac{π}{4}}^{\frac{π}{2}} - \ln \frac{\sqrt{2}}{2} = \frac{π}{4} - \ln \frac{\sqrt{2}}{2} = \frac{1}{4} π + \frac{1}{2} . \ln 2 = m . π + n . \ln 2 \Rightarrow \{\begin{array}{l} m = \frac{1}{4} \\ n = \frac{1}{2} \end{array} \Rightarrow P = 1 .$

Câu 26:

Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): mx + 2y - z + 1 = 0 (m là tam số). Mặt phẳng (P) cắt mặt cầu (S): ${(x - 2)}^{2} + {(y - 1)}^{2} + z^{2} = 9$ theo một đường tròn có bán kính bằng 2. Tìm tất cả các giá trị thực của tham số m.

A. $m = \pm 1$

B. $m = \pm 2 + \sqrt{5}$

C. $m = 6 \pm 2 \sqrt{5}$

D. $m = \pm 4$

Xem đáp án

Đáp án C.

Mặt cầu (S) có tâm I(2;1;0) bán kính R = 3. Ta có $d (I; (P)) = \sqrt{3^{2} - 2^{2}} = \sqrt{5}$

Do đó $\frac{|2 m + 3|}{\sqrt{m^{2} + 5}} = \sqrt{5} \Leftrightarrow {(2 m + 3)}^{2} = 5 m^{2} + 25 \Leftrightarrow m = 6 \pm 2 \sqrt{5} .$

Câu 27:

Đồ thị hàm số $y = - x^{3} + 3 m x + 1$ có 2 điểm cực trị A,B $(x_{A} < x_{B})$ sao cho tứ giác ABOE là hình bình hạnh với O là gốc tọa độ và điểm E(-4;-32). Tìm tất cả các giá trị thực của tham số m.

A. m = 1

B. m = 4

C. m = 2

D. $m \in \emptyset$

Xem đáp án

Đáp án B.

Ta có $y' = - 3 x^{2} + 3 m; y' = 0 \Leftrightarrow [\begin{array}{l} x = \sqrt{m} \Rightarrow y = 2 m \sqrt{m} + 1 \Rightarrow B (\sqrt{m}; 2 m \sqrt{m} + 1) \\ x = - \sqrt{m} \Rightarrow y = - 2 m \sqrt{m} + 1 \Rightarrow A (- \sqrt{m}; - 2 m \sqrt{m} + 1) \end{array}$

Do ABOE là hình bình hành nên $A B = E O \Rightarrow \{\begin{cases} 2 \sqrt{m} = 4 \\ 4 m \sqrt{m} = 32 \end{cases} \Rightarrow m = 4 .$

Câu 28:

Tìm nguyên hàm của hàm số $f (x) = \sqrt{x} \ln x .$

A. $\int f (x) d x = \frac{1}{9} x^{\frac{3}{2}} (3 \ln x - 2) + C$

B. $\int f (x) d x = \frac{2}{3} x^{\frac{3}{2}} (3 \ln x - 2) + C$

C. $\int f (x) d x = \frac{2}{9} x^{\frac{3}{2}} (3 \ln x - 1) + C$

D. $\int f (x) d x = \frac{2}{9} x^{\frac{3}{2}} (3 \ln x - 2) + C$

Xem đáp án

Đáp án D.

$\int f (x) d x = \int \sqrt{x} \ln x d x = \int \ln x d (\frac{2}{3} x^{\frac{3}{2}}) = \frac{3}{2} \ln x . x^{\frac{3}{2}} - \frac{2}{3} \int x^{\frac{3}{2}} d (\ln x) = \frac{2}{3} \ln x . x^{\frac{3}{2}} - \frac{2}{3} x^{\frac{1}{2}} d x \frac{2}{3} \ln x . x^{\frac{3}{2}} - \frac{2}{3} . \frac{2}{3} x^{\frac{3}{2}} + C = \frac{2}{9} x^{\frac{3}{2}} (3 \ln x - 2) + C .$

Câu 29:

Có bao nhiêu số phức z thỏa mãn $|z| = |z + z| = 1$ ?

A. 0

B. 1

C. 4

D. 3

Xem đáp án

Đáp án C.

Đặt z = a + bi với $a, b \in ℝ \Rightarrow z = a - b i \Rightarrow z + z = 2 a .$

Ta có: $|z| = |z + z| = 1 \Leftrightarrow \{\begin{cases} a^{2} + b^{2} = 1 \\ 4 a^{2} = 1 \end{cases} \Leftrightarrow \{\begin{cases} a^{2} = \frac{1}{4} \\ b^{2} = \frac{3}{4} \end{cases} \Leftrightarrow \{\begin{array}{l} a = \pm \frac{1}{2} \\ b = \pm \frac{\sqrt{3}}{2} \end{array} .$

Vậy có tất cả 4 số phức thảo mãn.

Câu 30:

Tập hợp các điểm biểu diễn số phức z thỏa mãn $2 |z - 1| = |z + z + 2|$ trên mặt phẳng tọa độ là một

A. đường thẳng

B. đường tròn

C. parabol

D. hypebol

Xem đáp án

Đáp án C.

Đặt z = a + bi với $a, b \in ℝ \Rightarrow \vec{z} = a - b i \Rightarrow z + \vec{z} + 2 = 2 a + 2 .$

Ta có: $2 |z - 1| = |z + \bar{z} + 2| \Leftrightarrow 2 |(a - 1) + b i| = 2 |a + 1| \Leftrightarrow {(a - 1)}^{2} + b^{2} = {(a + 1)}^{2} \Leftrightarrow b^{2} = 4 a .$

Vậy quỹ tích là một parabol.

Câu 31:

Người thợ gia công của một cơ sở chất lượng cao X cắt một miếng tôn hình tròn với bán kính 60cm thành ba miền hình quạt bằng nhau. Sau đó người thợ ấy quấn và hàn ba miếng tôn đó để được ba cái phễu hình nón. Hỏi thể tích V của mỗi cái phễu đó bằng bao nhiêu?

A. $V = \frac{16000 \sqrt{2}}{3} l í t$

B. $V = \frac{16 \sqrt{2}}{3} l í t$

C. $V = \frac{16000 \sqrt{2} π}{3} l í t$

D. $V = \frac{160 \sqrt{2 π}}{3} l í t$

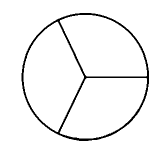
Xem đáp án

Đáp án B.

Ba hình quạt, mỗi hình quạt có độ dài cung là $L = φ R = 6 . \frac{2 π}{3} = 4 π dm .$

Mà độ dài cung chính là chu vi đáy của hình nón $\Rightarrow L = C = 2 πr \Rightarrow r = 2 dm$ .

Suy ra chiều cao của hình nón là $h = \sqrt{1^{2} - r^{2}} = \sqrt{R^{2} - r^{2}} = 4 \sqrt{2} d m$ .

Vậy thể tích cần tính là $V = \frac{1}{3} {πr}^{2} h = \frac{π}{3} . 2^{2} . 4 \sqrt{2} = \frac{16 \sqrt{2} π}{3}$ lít.

Câu 32:

Cho hàm số $f (x) = x^{3} - 6 x^{2} + 9 x + 1$ có đồ thị (C). Có bao nhiêu tiếp tuyến của đồ thị (C) tại điểm thuộc đồ thị (C) có tung độ là nghiệm phương trình $2 f' (x) - x . f'' (x) - 6 = 0$ ?

A. 1

B. 4

C. 2

D. 3

Xem đáp án

Đáp án A.

Ta có $f' (x) = 3 x^{2} - 12 x + 9 \Rightarrow f'' (x) = 6 x + 12; \forall x \in ℝ$ .

Khi đó $2 f' (x) - x . f'' (x) - 6 = 0 \Leftrightarrow 2 (2 x^{2} - 12 x + 9) - x (6 x - 12) - 6 = 0 \Leftrightarrow x = 1 .$

Theo bài ra, ta có $f (x_{0}) = 1 \Leftrightarrow {x_{0}}^{3} - 6 {x_{0}}^{2} + 9 x_{0} + 1 = 1 \Rightarrow [\begin{array}{l} x_{0} = 0 \\ x_{0} = 3 \end{array} .$

Vậy có 2 tiếp tuyến của đồ thị hàm số (C) đi qua điểm có tung độ bằng 1.

Câu 33:

Ông An muốn xây một cái bể chứa nước lớn dạng một khối hộp chữ nhật không nắp có thể tích bằng 288 $m^{3}$ . Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây bể là 500.000 đồng/ $m^{2}$ . Nếu ông An biết xác định các kích thước của bể hợp lí thì chi phí thuê nhân công sẽ thấp nhất. Hỏi ông An trả chi phí thấp nhất để xây dựng bể đó là bao nhiêu?

A. 108 triệu đồng

B. 54 triệu đồng

C. 168 triệu đồng

D. 90 triệu đồng

Xem đáp án

Đáp án A.

Gọi x,y,h lần lượt là chiều rộng, chiều dài của đáy và chiều cao của hình hộp chữ nhật.

Theo bài ra, ta có $\{\begin{cases} y = 2 x \\ x y h = 288 \end{cases} \Leftrightarrow \{\begin{cases} y = 2 x \\ 2 x^{2} . h = 288 \end{cases} \Leftrightarrow \{\begin{cases} y = 2 x \\ h = \frac{144}{x^{2}} \end{cases}$

Diện tích bể cần xây là $S = S_{x q} + S_{đ} = 2 x h + 2 y h + x y = 2 x^{2} + \frac{864}{x} .$

Ta có $x^{2} + \frac{216}{x} + \frac{216}{x} \geq \sqrt[3]{x^{2} . \frac{216}{x} . \frac{216}{x}} = 108 \Rightarrow S = 2.108 = 216 m^{2}$ .

Vậy ông An trả chi phí thấp nhất là 500.000 x 216 = 108 triệu đồng.

Câu 34:

Trong không gian với hệ tọa độ Oxyz , cho đường thẳng $d : \frac{x - 1}{1} = \frac{y - 2}{1} = \frac{z - 1}{2}$ , A(2;1;4). Gọi điểm H(a;b;c) là điểm thuộc d sao cho AH có độ dài nhỏ nhất. Tính giá trị T = $a^{2} + b^{2} + c^{2}$ .

A. T = 8

B. T = 62

C. T = 13

D. T = $\sqrt{5}$

Xem đáp án

Đáp án B.

Để $A H_{m i n} \Leftrightarrow$ H là hình chiếu của A trên d.

Gọi $(α)$ là mặt phẳng đi qua A và vuông góc với d

Suy ra $\vec{n} (α) = {\vec{u}}_{đ} = (1; 1; 2) \Rightarrow (α) : 1 . (x - 2) + 2 . (y - 1) + 2 . (z - 4) = 0 \Leftrightarrow x + y + 2 z - 11 = 0$ .

Mặt khác $H = d \cap (α) \Rightarrow H (2; 3; 3) \Rightarrow \{\begin{cases} a = 2 \\ b = c = 3 \end{cases} \Rightarrow T = 62 .$

Câu 35:

Cho hàm số $f (x) = 5^{x} . 8^{2 x^{3}}$ . Khẳng định nào sau đây là sai?

A. $f (x) \leq 1 \Leftrightarrow x \log_{2} 5 + 2 x^{3} \leq 0 .$

B. $f (x) \leq 1 \Leftrightarrow x + 6 x^{3} \log_{5} 2 \leq 0 .$

C. $f (x) \leq 1 \Leftrightarrow x \log_{2} 5 + 6 x^{3} \leq 0 .$

D. $f (x) \leq 1 \Leftrightarrow x \log_{2} \sqrt{5} + 3 x^{3} \leq 0 .$

Xem đáp án

Đáp án A.

Ta có $f (x) \leq 1 \Leftrightarrow 5^{x} . 8^{2 x^{3}} \leq 1 \Leftrightarrow \log_{2} (5^{x} . 8^{2 x^{3}}) \leq 0 \Leftrightarrow x \log_{2} 5 + 2 x^{3} \log_{2} 8 \leq 0 \Leftrightarrow x \log_{2} 5 + 6 x^{3} \leq 0 .$

Hoặc $\log_{5} (5^{x} . 8^{2 x^{3}}) \leq 0 \Leftrightarrow x + \log_{5} 8^{2 x^{3}} \leq 0 \Leftrightarrow x + 6 x^{3} \log_{5} 2 \leq 0 .$

Câu 36:

Có bao nhiêu giá trị nguyên của tham số m để hàm số $f (x) = 2 x^{3} - 6 x^{2} - m + 1$ có các giá trị cực trị trái dấu?

A. 2.

B. 9.

C. 3.

D. 7.

Xem đáp án

Đáp án D.

Ta có $f' (x) = 6 x^{2} - 12 x; f' (x) = 0 \Leftrightarrow [\begin{array}{l} x = 0 \Rightarrow y (0) = 1 - m \\ x = 2 \Rightarrow y (2) = - 7 - m \end{array} .$

Theo bài ra, ta có $y (0) . y (2) < 0 \Leftrightarrow (1 - m) (- 7 - m) < 0 \Leftrightarrow - 7 < m < 1 .$

Câu 37:

Cho hàm số f(x) liên tục trên $ℝ$ và $\int_{0}^{1} f (x) d x = 2$ ; $\int_{0}^{3} f (x) d x = 6$ . Tính $I = \int_{- 1}^{1} f (|2 x - 1|) d x$ ?

A. $I = \frac{2}{3}$

B. $I = 4$

C. $I = \frac{3}{2}$

D. $I = 6$

Xem đáp án

Đáp án B.

Đặt $t = 2 x - 1 \Leftrightarrow d t = 2 d x$ và đổi cận $\{\begin{cases} x = - 1 \Rightarrow t = - 3 \\ x = 1 \Rightarrow t = 1 \end{cases}$

Khi đó $I = \frac{1}{2} \int_{- 3}^{1} f (|t|) d t = \frac{1}{2} \int_{- 3}^{0} f (- t) d t + \frac{1}{2} \int_{0}^{1} f (t) d t = \frac{1}{2} (\int_{0}^{3} f (t) d t + \int_{0}^{1} f (t) d t) = 4 .$

Câu 38:

Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy bằng a, cạnh bên bằng $a \sqrt{3}$ . Gọi O là tâm của đáy ABC, $d_{1}$ là khoảng cách từ A đến mặt phẳng (SBC), $d_{2}$ là khoảng cách từ O đến mặt phẳng (SBC). Tính $d = d_{1} + d_{2}$ ?

A. $d = \frac{2 a \sqrt{22}}{11}$ .

B. $d = \frac{2 a \sqrt{22}}{33}$

C. $d = \frac{8 a \sqrt{22}}{33}$

D. $d = \frac{8 a \sqrt{22}}{11}$

Xem đáp án

Đáp án C.

Gọi O là tâm của tam giác đều ABC.

Do hình chóp S.ABC đều nên suy ra $S O ⊥ (A B C)$ .

Ta có $d (A; (S B C)) = 3 \times d (O; (S B C)) .$

Gọi E là trung điểm BC; Kẻ $O K ⊥ S E \Rightarrow d (O; (S B C)) = O K .$

Tính được $S O = \sqrt{S A^{2} - O A^{2}} = \frac{2 \sqrt{6}}{3}$ và $O E = \frac{1}{3} A E = \frac{a \sqrt{3}}{6}$ .

Tám giác vuông SOE, có $O K = \frac{S O . O E}{\sqrt{S O^{2} + O E^{2}}} = \frac{2 a \sqrt{22}}{33}$ .

Vậy $d = d_{1} + d_{2} = 4 d_{2} = \frac{8 a \sqrt{22}}{22}$ .

Câu 39:

Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \frac{\sqrt{x^{2} - 1}}{x - 2}$ trên tập hợp $D = (- \infty; - 1) \cup [1; \frac{3}{2}]$ . Tính giá trị P = M.n?

A. $P = \frac{1}{9}$

B. $P = \frac{3}{2}$

C. $P = 0$

D. $P = - \frac{3}{2}$

Xem đáp án

Đáp án C.

Xét hàm số $y = \frac{\sqrt{x^{2} - 1}}{x - 2}$ trên D, có $f' (x) = \frac{1 - 2 x}{{(x - 2)}^{2} \sqrt{x^{2} - 1}}; \forall x \in D$ .

Trên khoảng $(- \infty; - 1);$ có $f' (x) > 0 \Rightarrow f (x)$ là hàm số đồng biến trên $(- \infty; - 1)$

Trên khoảng $[1; \frac{3}{2}]$ , có $f' (x) < 0 \Rightarrow f (x)$ f(x) là hàm số nghịch biến trên $[1; \frac{3}{2}]$ .

Dựa vào BBT, suy ra $M = f (1) = 0$ và $m = f (\frac{3}{2}) = - \sqrt{5}$ . Vậy P = M.m = 0

Câu 40:

Đồ thị hàm số $y = a x^{4} + b x^{2} + c$ đạt cực đại tại A(0;-2) và cực tiểu tại $B (\frac{1}{2}; - \frac{17}{8})$ . Tính a + b + c

A. a + b + c = 2

B. a + b + c = 0

C. a + b + c = -1

D. a + b + c = -3

Xem đáp án

Đáp án C.

Xét hàm số $y = a x^{4} + b x^{2} + c$ , ta có $y' = 4 a x^{3} + 2 b x; y'' = 12 a x^{2} + 2 b; \forall x \in ℝ .$

Điểm A(0;-2) là điểm cực đại của đồ thị hàm số $\Rightarrow \{\begin{array}{l} y' (0) = 0 \Leftrightarrow \\ y (0) = - 2 \\ y'' (0) < 0 \end{array} \Leftrightarrow \{\begin{cases} c = - 2 \\ b > 0 \end{cases} .$

Điểm B( $\frac{1}{2}; - \frac{17}{8}$ ) là điểm cực tiểu của đồ thị hàm số $\Rightarrow \{\begin{cases} y' (\frac{1}{2}) = 0; y (\frac{1}{2}) = - \frac{17}{8} \\ y'' (0) > 0 \end{cases}$

$\Leftrightarrow \{\begin{cases} \frac{a}{2} + b = 0 \\ \frac{a}{16} + \frac{b}{4} + c = - \frac{17}{8} \end{cases} \Leftrightarrow \{\begin{cases} a + 2 b = 0 \\ a + 4 b = - 2 \end{cases} \Leftrightarrow \{\begin{cases} a = 2 \\ b = - 1 \end{cases} \Rightarrow a + b + c = - 1 .$

Câu 41:

Một cái th ng đựng nước được tạo thành từ việc cắt mặt xung quanh của một hình nón bởi một mặt phẳng vuông góc với trục của hình nón. Miệng thùng là đường tròn có bán kính bằng hai lần bán kính mặt đáy của th ng. Bên trong thùng có một cái phễu dạng hình nón có đáy là đáy của th ng, có đ nh là tâm của miệng thùng và có chiều cao bằng 20cm (xem hình minh họa). Biết rằng đổ 4.000 $c m^{3}$ nước vào th ng thì đầy th ng (nước không chảy được vào bên trong phễu), tính bán kính đáy r của phễu (giá trị gần đúng của r làm tròn đến hàng phần trăm).

A. r = 9,77 cm

B. r = 7,98 cm

C. r = 5,64 cm

D. r = 5,22 cm

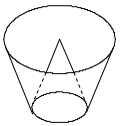
Xem đáp án

Đáp án C.

Gọi $R_{1} = r$ là bán kính đường tròn đáy của hình nón và cũng là bán kính mặt đáy của thùng.

Khi đó $R_{2} = 2 r$ là bán kính của miệng thùng và phễu, thùng có cùng chiều cao h = 20 cm.

Thể tích của thùng là $V_{1} = \frac{1}{3} πh ({R_{1}}^{2} + {R_{2}}^{2} + R_{1} R_{2}) = \frac{1}{2} . π . 20 . (r^{2} + 4 r^{2} + r . 2 r) = \frac{140 π}{3} . r^{2} {cm}^{3} .$

Thẻ tích của phễu hình nón là $V_{2} = \frac{1}{3} {πR}_{1}^{2} h = \frac{1}{3} . π . r^{2} . 20 = \frac{20 π}{3} . r^{2} {cm}^{3} .$

Vậy thể tích khối nước là $V = V_{1} - V_{2} = 40 {πr}^{2} = 4000 \Rightarrow r = \sqrt{\frac{100}{π}} \approx 5, 64 cm .$

Câu 42:

Cho tam giác SAB vuông tại A, ABS = 60 $°$ đường phân giác trong của ABS cắt SA tại điểm I. Vẽ nửa đường tròn tâm I bán kính IA (như hình vẽ). Cho $∆ S A B$ và nửa đường tròn trên quay quanh cạnh SA tạo nên các khối tròn xoay tương ứng có thể tích $V_{1}, V_{2}$ . Khẳng định nào dưới đây đúng?

A. $4 V_{1} = 9 V_{2}$

B. $9 V_{1} = 4 V_{2}$

C. $V_{1} = 3 V_{2}$

D. $2 V_{1} = 3 V_{2}$

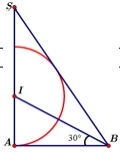
Xem đáp án

Đáp án A.

Đặt SA = h tam giác SAB vuông tại A $\Rightarrow A B = \frac{S A}{\tan 60 °} = \frac{h}{\sqrt{3}} .$

Tam giác IAB vuông tại A $\Rightarrow \tan \hat{I B A} = \frac{I A}{A B} \Rightarrow I A = \frac{h}{3} .$

Khi quay tam giác SAB quay trục SA, ta được khối nón có chiều cao h, bán kính $r = \frac{h}{\sqrt{3}}$ ,

Và quay nửa đường tròn quanh trục SA, ta được khối cầu có bán kính $R = \frac{h}{3}$ .

Vậy $\{\begin{cases} V_{1} = \frac{1}{3} {πr}^{2} h = \frac{1}{3} π . {(\frac{h}{\sqrt{3}})}^{2} h = \frac{{πh}^{3}}{9} \\ V_{2} = \frac{4}{3} {πR}^{2} = \frac{4}{3} π {(\frac{h}{3})}^{3} = \frac{4 {πh}^{3}}{81} \end{cases} \Rightarrow \frac{V_{1}}{V_{2}} = \frac{1}{9} : \frac{4}{81} = \frac{9}{4} \Rightarrow 4 V_{1} = 9 V_{2} .$

Câu 43:

Trong không gian với hệ tọa độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua điểm M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với điểm gốc tọa độ sao cho M là trực tâm tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P).

A. $3 x + 2 y + z + 14 = 0$

B. $2 x + y + 3 z + 9 = 0$

C. $3 x + 2 y + z - 14 = 0$

D. $2 x + y + z - 9 = 0$

Xem đáp án

Đáp án A.

Ta có $A M ⊥ B C ⊥ O A \Rightarrow B C ⊥ (O A M) \Rightarrow B C ⊥ O M$

Tương tự ta cũng có $O M ⊥ A C \Rightarrow O M ⊥ (P) \Rightarrow (P)$ (P) nhận $\bar{O M} = (3; 2; 1)$ là vecto pháp tuyến.

Trong các đáp án, chọn đáp án mặt phẳng có vecto pháp tuyến có cùng giá với $\bar{O M}$ và không chứa điểm M thì thỏa.

Câu 44:

Có bao nhiêu giá trị thực của tham số m để đồ thị hàm số $y = x^{4} - 2 m x^{2} + m - 1$ có ba điểm cực trị tạo thành một tam giác có bán kính đường tròn ngoại tiếp chúng bằng 1?

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Đáp án B.

Xét hàm số $y = x^{4} - 2 m x^{2} + m - 1$ , có $y' = 4 x^{3} - 4 m x = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ x^{2} = m \end{array} .$

Để hàm số có 3 điểm cực trị khi và chỉ khi m > 0.

Khi đó, gọi A(0;m - 1), B( $\sqrt{m}; - m^{2} + m - 1$ ) và $C (- \sqrt{m}; - m^{2} + m - 1)$ là 3 điểm cực trị của ĐTHS.

Gọi H là trung điểm của BC suy ra $H (0; - m^{2} + m - 1) \Rightarrow A H = m^{2} .$

Diện tích tam giác ABC là $S_{∆ A B C} = \frac{1}{2} . A H . B C = \frac{1}{2} m^{2} . 2 \sqrt{m} = m^{2} \sqrt{m} .$

Và $A B = A C = \sqrt{m^{4} + m}$ suy ra $S_{∆ A B C} = \frac{A B . A C . B C}{4 R_{∆ A B C}} \Rightarrow A B^{2} . B C = 4 S_{∆ A B C}$

$\Leftrightarrow (m^{4} + m) . 2 \sqrt{m} = 4 m^{2} \sqrt{m} \Leftrightarrow m^{4} - 2 m^{2} + m = 0 \Leftrightarrow m (m^{3} - 2 m + 1) = 0 .$

Kết hợp với m > 0 suy ra có 2 giá trị m cần tìm.

Câu 45:

Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} + a x + b y + c z + d = 0$ có bán kính $R = \sqrt{19}$ , đường thẳng $d : \{\begin{cases} x = 5 + t \\ y = - 2 - 4 t \\ z = - 1 - 4 t \end{cases}$ và mặt phẳng $(P) : 3 x - y - 3 z - 1 = 0$ . Trong các số {a,b,c,d} theo thứ tự dưới đây, số nào thỏa mãn a + b + c + d = 43, đồng thời tâm I của (S) thuộc đường thẳng d và (S) tiếp xúc với (P)?

A. {-6;-12;-14;75}

B. {6;10;20;7}

C. {-10;4;2;47}

D. {3;5;6;29}

Xem đáp án

Đáp án A.

Ta có $(S) : {(x + \frac{a}{2})}^{2} + {(y + \frac{b}{2})}^{2} + {(z + \frac{c}{2})}^{2} = \frac{a^{2} + b^{2} + c^{2}}{4} - d$ có $I (- \frac{a}{2}; - \frac{b}{2}; - \frac{c}{2})$

Vì $I \in d \Rightarrow I (5 + t; - 2 - 4 t; - 1 - 4 t)$ và (S) tiếp xúc với (P) nên $d (I; (P)) = R$

$\frac{|3 . (5 + t) - (- 2 - 4 t) - 3 . (- 1 - 4 t) - 1|}{\sqrt{3^{2} + {(- 1)}^{2} + {(- 3)}^{2}}} = \sqrt{19} \Leftrightarrow |t + 1| = 1 \Leftrightarrow [\begin{array}{l} t = 0 \\ t = 2 \end{array}$

$\Rightarrow [\begin{array}{l} I (5; - 2; - 1) \\ I (3; 6; 7) \end{array} \Rightarrow [\begin{array}{l} (a, b, c, d) = (- 10; 4; 2; 47) \\ (a, b, c, d) = (- 6; - 12; - 14; 75) \end{array}$

Thử lại với $\frac{a^{2} + b^{2} + c^{2}}{4} - d = R^{2} = 19$ thì chỉ có trường hợp {-6;-12;-14;75} thỏa

Câu 46:

Cho phương trình $(m + 1) \log_{2}^{2} x + 2 \log_{2} x + (m - 2) = 0$ . Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình đã cho có hai nghiệm thực $x_{1}, x_{2}$ thỏa $0 < x_{1} < 1 < x_{2}$ .

A. $(2; + \infty)$

B. $(- 1; 2)$

C. $(- \infty; - 1)$

D. $(- \infty; - 1) \cup (2; + \infty)$

Xem đáp án

Đáp án B.

Đặt $t = \log_{2} x$ , khi đó $(m + 1) {\log_{2}}^{2} x + 2 \log_{2} x + m - 2 = 0 \Leftrightarrow (m + 1) t^{2} + 2 t + m - 2 = 0$ (*).

Để phương trình (*) có hai nghiệm phân biệt $\Leftrightarrow \{\begin{cases} a = m + 1 \neq 0 \\ ∆' = 1 - (m + 1) (m - 2) > 0 \end{cases} \Leftrightarrow \{\begin{cases} m \neq - 1 \\ m^{2} - m - 3 < 0 \end{cases} (1) .$

Khi đó gọi $x_{1}; x_{2}$ lần lượt hai nghiệm của phương trình (*).

Vì $0 < x_{1} < 1 < x_{2}$ suy ra $\{\begin{cases} t_{1} = \log_{2} x_{1} < 0 \\ t_{2} = \log_{2} x_{2} > 0 \end{cases} \Rightarrow t_{1} t_{2} = \frac{c}{a} = \frac{m - 2}{m + 1} < 0 (2) .$

Từ (1), (2) suy ra $- 1 < m < 2 \Leftrightarrow m \in (- 1; 2)$ là giá trị cần tìm.

Câu 47:

Cho số phức z thỏa mãn $|z - 2 - 3 i| = 1$ . Gọi $M = m a x |\bar{z} + 1 + i|$ , $m = m i n |\bar{z} + 1 + i|$ . Tính giá trị của biểu thức $(M^{2} + m^{2})$

A. $M^{2} + m^{2} = 28$

B. $M^{2} + m^{2} = 26$

C. $M^{2} + m^{2} = 24$

D. $M^{2} + m^{2} = 20$

Xem đáp án

Đáp án A.

Ta có $1 = {|z - 2 - 3 i|}^{2} = (z - 2 - 3 i) . \bar{(z - 2 - 3 i)} = (z - 2 - 3 i) (\bar{z} - \bar{2 + 3 i}) = (z - 2 - 3 i) (\bar{z} - 2 + 3 i)$

Lấy môđun hai vế, ta được $|z - 2 - 3 i| . |\bar{z} - 2 + 3 i| = 1 \Leftrightarrow |\bar{z} - 2 + 3 i| = 1 (*)$

Đặt $w = \bar{z} + 1 + i \Leftrightarrow \bar{z} = w - 1 - i$ , khi đó (*) $\Leftrightarrow |w - 1 - 2 - 3 i| = 1 \Leftrightarrow |w - 3 + 2 i| = 1$ .

$\Rightarrow \{\begin{cases} {|w|}_{m i n} = \sqrt{3^{2} + 2^{2}} - 1 = \sqrt{13} - 1 \\ {|w|}_{m i n} = \sqrt{3^{2} + 2^{2}} - 1 = \sqrt{13} + 1 \end{cases} \Rightarrow \{\begin{array}{l} M = \sqrt{13} + 1 \\ m = \sqrt{13} - 1 \end{array} \Rightarrow M^{2} + m^{2} = {(\sqrt{13} + 1)}^{2} + {(\sqrt{13} - 1)}^{2} = 28 .$

Câu 48:

Trong không gian với hệ tọa độ Oxyz, cho điểm A(9;-3;5), B(a,b,c). Gọi M, N, P lần lượt là giao điểm của đường thẳng AB với các mặt phẳng tọa độ (Oxy);(Oxz);(Oyz). Biết M,N,P nằm trên đoạn AB sao cho AN = MN = NP = PB. Giá trị của tổng a + b + c là

A. -21

B. 15

C. 21

D. -15

Xem đáp án

Đáp án D.

Vì $M \in (O x y), M \in (O x z), P \in (O y z) \Rightarrow z_{M} =, y_{N} = 0, z_{P} = 0$

Mà M,N,P nằm trên đoạn AB sao cho $A M = M N = N P = P B \Rightarrow \bar{A M} = \bar{M N} = \bar{N P} = \bar{P B}$

Khi đó $\bar{A B} = 4 \bar{A M} \Rightarrow c - 5 = 4 (z_{M} - 5) \Rightarrow c = - 15 .$

Lại có: $\bar{A B} = 2 \bar{A N} \Rightarrow b + 3 = 2 (y_{N} + 3) \Rightarrow b = 3 .$

$\bar{A B} = 4 \bar{P B} \Rightarrow a - 9 = 4 (a + x_{P}) \Rightarrow a = - 3 \Rightarrow a + b + c = - 15 .$

Câu 49:

Cho số phức z thỏa mãn $|\frac{z - 1}{2 - i} + i| = \sqrt{5}$ . Biết rằng tập hợp biểu diễn số phức w = (1 - i)z + 2i có dạng ${(x + 2)}^{2} + y^{2} = k$ . Tìm k.

A. k = 92

B. k = 100

C. k = 50

D. k = 96

Xem đáp án

Đáp án C.

Ta có $|\frac{z - 1}{2 - i} + i| = \sqrt{5} \Leftrightarrow |z + 2 i| = 5 \Rightarrow |w + 2| = |(1 - i) (z + 2 i)| = 5 \sqrt{2}$ . Vậy tập hợp điểm biểu diễn số phức w là đường tròn tâm I(-2;0) bán kính $R = 5 \sqrt{2}$ , tức là đường tròn $(C) : {(x + 2)}^{2} + y^{2} = 50$ .

Câu 50:

Đặt $f (n) = {(n^{2} + n + 1)}^{2} + 1$ . Xét dãy số $(u_{n})$ sao cho $u_{n} = \frac{f (1) f (3) f (5) . . . f (2 n - 1)}{f (2) f (4) f (6) . . . f (2 n)}$ . Tính $l i m (n \sqrt{n_{n}})$ .

A. $l i m (n \sqrt{n_{n}}) = \sqrt{2}$

B. $l i m (n \sqrt{n_{n}}) = \frac{1}{\sqrt{3}}$

C. $l i m (n \sqrt{n_{n}}) = \sqrt{3}$

D. $l i m (n \sqrt{n_{n}}) = \frac{1}{\sqrt{2}}$

Xem đáp án

Đáp án D.

Ta có phân tích $f (n) = {(n^{2} + n + 1)}^{2} + 1 = n^{4} + 2 n^{2} (n + 1) + {(n + 1)}^{2} + 1$

$= n^{2} (n^{2} + 2 n + 2) + {(n + 1)}^{2} + 1 = n^{2} [{(n + 1)}^{2} + 1] + {(n + 1)}^{2} + 1 = (n^{2} + 1) [{(n + 1)}^{2} + 1]$

Khi đó $\frac{f (2 k - 1)}{f (2 k)} = \frac{{(2 k - 1)}^{2} + 1}{{(2 k + 1)}^{2} + 1} \Rightarrow u_{n} = \frac{1^{2} + 1}{3^{2} + 1} . \frac{3^{2} + 1}{5^{2} + 1} . . . \frac{{(2 n - 1)}^{2} + 1}{{(2 n + 1)}^{2} + 1} = \frac{1}{2 n^{2} + 2 n + 1}$

$\Rightarrow l i m (n \sqrt{u_{n}}) = l i m \frac{n}{\sqrt{2 n^{2} + 2 n + 1}} = \frac{1}{\sqrt{2}} .$