50 câu hỏi trắc nghiệm thuộc Tổng hợp đề thi thptqg môn Toán cực hay mới nhất (Đề số 04)

Câu 1:

Biết rằng đường thẳng $d : \{\begin{cases} x = 2 + 3 t \\ y = t \\ z = - 1 - t \end{cases}$ là tiếp tuyến của mặt cầu tâm $I (0; 0; 1)$ . Bán kính $ℝ$ của mặt cầu đó là

A. $\frac{2 \sqrt{66}}{11}$

B. $\frac{3 \sqrt{2}}{11}$

C. $\frac{2 \sqrt{6}}{11}$

D. $\frac{2 \sqrt{53}}{11}$

Xem đáp án

Câu 2:

Cho hai đường thẳng a, b song song với nhau. Trên a ta chọn 10 điểm phân biệt, trên b ta chọn 11 điểm phân biệt. Có bao nhiêu hình thang được tạo thành từ 21 điểm đã cho ở trên?

A. 406

B. 2475

C. 2512

D. 304

Xem đáp án

Đáp án B

Chọn 2 điểm bất kì thuộc a và 2 điểm bất kì thuộc b ta được 1 hình thang, như vậy số cách chọn là

$C_{10}^{2} C_{11}^{2} = 2475$ cách chọn.

Câu 3:

Gọi D là miền phẳng giới hạn bởi đồ thị các hàm số $y = \sqrt{cosx}$ , $y = 0, x = 0$ và $x = \frac{π}{4}$ . Tính thể tích của khối tròn xoay khi quay D quanh trục hoành.

A. $\frac{\sqrt{2} π}{2}$

B. $\sqrt{2} π$

C. $\frac{π}{2}$

D. $\frac{π}{2 \sqrt{2}}$

Xem đáp án

Câu 4:

Cho hàm số $y = x^{4} - 4 x^{2} - 1$ . Gọi $h_{1}, h_{2}$ lần lượt là khoảng cách từ hai điểm cực đại và cực tiểu của đồ thị hàm số đến trục hoành. Khi đó tỷ số $\frac{h_{1}}{h_{2}}$ bằng

A. 5

B. $\frac{1}{\sqrt{2}}$

C. $- \frac{1}{5}$

D. $\frac{1}{5}$

Xem đáp án

Câu 5:

Xác định m để đường thẳng $d : \frac{x - 2}{2} = \frac{y - 1}{1} = \frac{z}{3}$ cắt mặt phẳng $(P) : x + my - z + 1 = 0$

A. $m \neq 1$

B. $m \neq - 1$

C. $m \neq 0$

D. Với mọi giá trị của m

Xem đáp án

Câu 6:

Cho hàm số $f (x) = \frac{1}{3 - 2 x}$ . Gọi $F (x)$ là một nguyên hàm của hàm số $f (x)$ . Chọn phương án đúng.

A. $F (x) = \frac{1}{2} \ln |3 - 2 x| - 1$

B. $F (x) = \frac{\ln^{2} (3 - 2 x)}{4} + 1$

C. $F (x) = - \frac{1}{2} \ln |3 - 2 x| + \frac{1}{2}$

D. $F (x) = - \ln (3 - 2 x)$

Xem đáp án

Câu 7:

Đồ thị hàm số $y = |x^{3}| - 3 x^{2} + 1$ có bao nhiêu điểm cực trị?

A. 2

B. 3

C. 1

D. 4

Xem đáp án

Giữ nguyên phần bên phải trục tung và lấy đối xứng với phần bên phải Oy qua Oy.

Như vậy ta sẽ được đồ thị hàm số $y = |x^{3}| - 3 x^{2} + 1$ có dạng như sau:

Câu 8:

Cho hàm số $f (x) = 2 mx + lnx$ . Tìm giá trị thực của tham số m để nguyên hàm $F (x)$ của $f (x)$ thỏa mãn $F (1) = 0$ và $F (2) = 2 + 2 \ln 2$

A. m = 2

B. m = 1

C. m = 0

D. m = $\frac{1}{2}$

Xem đáp án

Câu 9:

Tập xác định của hàm số $y = \frac{1}{\sqrt{\log_{x} (x - 1)} - 1}$ là

A. $x \geq 2$

B. $x > 1$ và $x \neq 2$

C. $x > 1$

D. $x > 2$

Xem đáp án

Câu 10:

Cho tập X là một tập hợp gồm n phần tử, n là số tự nhiên lớn hơn 2. Tìm n biết số tập con gồm 2 phần tử của tập hợp X bằng 45

A. 10

B. 30

C. 6

D. 20

Xem đáp án

Đáp án A

Số tập con gồm 2 phần tử của tập hợp n phần tử là $C_{n}^{2} = 45 \Rightarrow n = 10$

Câu 11:

Cho hình vuông ABCD có cạnh a, M là trung điểm của AD. Xét khối tròn xoay sinh bởi tam giác CDM (cùng các điểm trong của nó) khi quay quanh đường thẳng AB. Thể tích của khối tròn xoay đó bằng

A. $\frac{5 {πa}^{3}}{12}$

B. $\frac{3 {πa}^{3}}{4}$

C. $\frac{7 {πa}^{3}}{12}$

D. $\frac{{πa}^{3}}{3}$

Xem đáp án

Đáp án A

Khi quay quanh AB, hình vuông ABCD sinh ra mặt trụ có thể tích $V_{1} = {πa}^{3}$

Hình thang AMCB sinh ra hình nón cụt có thể tích

Câu 12:

Cho hàm số $y = \frac{x + 1}{x - 2}$ . Chọn khẳng định đúng

A. Hàm số có duy nhất một cực trị

B. Hàm số nghịch biến trên từng khoảng thuộc tập xác định

C. Đồ thị hàm số có đường tiện cận ngang là $x = 2$

D. Hàm số nghịch biến trên R

Xem đáp án

Câu 13:

Nghiệm âm lớn nhất của phương trình $2 \tan^{2} x + 5 tanx + 3 = 0$ là

A. $- \frac{5 π}{6}$

B. $- \frac{π}{3}$

C. $- \frac{π}{6}$

D. $- \frac{π}{4}$

Xem đáp án

Câu 14:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng $(P) : x - y - z + 1 = 0$ và $(Q) : 2 x + 3 y - z = 0$ . Viết phương trình chính tắc của đường thẳng giao tuyến Δ của hai mặt phẳng (P) và (Q). Chọn khẳng định sai.

A. $\frac{x - 1}{4} = \frac{y}{- 1} = \frac{z - 2}{5}$

B. $\frac{x}{- 4} = \frac{y - \frac{1}{4}}{1} = \frac{z - \frac{3}{4}}{- 5}$

C. $\frac{x}{4} = \frac{y}{- 1} = \frac{z - 1}{5}$

D. $\frac{x + \frac{3}{5}}{4} = \frac{y - \frac{2}{5}}{- 1} = \frac{z}{5}$

Xem đáp án

Câu 15:

Tìm tất cả các giá trị của tham số m để phương trình $9^{x} - (2 m + 1) 3^{x} + m + 1 = 0$ có hai nghiệm phân biệt.

A. $m > \frac{\sqrt{3}}{2}$

B. $m < - \frac{\sqrt{3}}{2}$

C. $m > - \frac{1}{2}$

D. $m > - 1$

Xem đáp án

Câu 16:

Cho hàm số $y = - x^{3} - 3 x^{2} + 4$ có đồ thị (C) là hình vẽ dưới đây. Với giá trị nào của m thì phương trình $x^{3} + 3 x^{2} + m = 0 (*)$ có hai nghiệm phân biệt?

A. m = 0 hoặc m = 4

B. m = 0 hoặc m = 6

C. m = -4 hoặc m = 0

D. m = -2 hoặc m = 4

Xem đáp án

Câu 17:

Cho hình chóp S.ABCD trong đó SA, AB, BC đôi một vuông góc với nhau và $SA = AB = BC = 1$ . Khoảng cách giữa hai điểm S và C nhận giá trị nào trong các giá trị sau?

A. 2

B. $\sqrt{3}$

C. $\sqrt{2}$

D. $\frac{\sqrt{3}}{2}$

Xem đáp án

Câu 18:

Tìm số phức z biết rằng điểm biểu diễn của z nằm trên đường tròn tâm O bán kính bằng 1 và nằm trên đường thẳng $x + y = \sqrt{2}$

A. $z = \sqrt{2} i$

B. $z = \frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2} i$

C. $z = \sqrt{2} - 1 + i$

D. $z = \sqrt{2}$

Xem đáp án

Câu 19:

Cho hàm số $f (x) = x^{5} + x - 1$ . Trong các mệnh đề sau, mệnh đề nào là SAI khi nói về nghiệm thực của phương trình $f (x) = 0$ ?

A. Phương trình có nghiệm trong khoảng $(0; 1)$

B. Phương trình có duy nhất một nghiệm

C. Phương trình có đúng 5 nghiệm

D. Phương trình có nghiệm trong khoảng $(- 1; 1)$

Xem đáp án

Câu 20:

Gọi $x_{1}, x_{2}, (x_{1} < x_{2})$ là hai nghiệm của phương trình $\sqrt[3]{{(3 - \sqrt{8})}^{x}} + {(\sqrt[3]{(3 + \sqrt{8})})}^{x} = 6 .$ Biểu thức ${P=2x}_{1} + x_{2}^{2}$ có giá trị là

A. 15

B. 0

C. 3

D. -3

Xem đáp án

Câu 21:

Trong các nhận định sau, nhận định nào dưới đây là sai?

A. Hàm số y=sinx và y=cosx đều có tính chất tuần hoàn

B. Hàm số y=sinx đồng biến trên khoảng $(\frac{π}{3}; \frac{7 π}{12})$

C. Hàm số y=sinx là một hàm số lẻ

D. Hàm số y=sinx có đồ thị là một đường hình sin

Xem đáp án

Câu 22:

Cho đồ thị hàm số $y = {ax}^{4} + {bx}^{2} + c$ đạt cực đại tại $A (0; 3)$ và đạt cực tiểu tại $B (1; - 3)$ . Tính giá trị của biểu thức $P = a + 3 b + 2 c .$

A. -9

B. 0

C. -24

D. -12

Xem đáp án

Câu 23:

Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = 2 - \sqrt{cosx}$ . Tính $M - m$ .

A. 2

B. -1

C. 1

D. 0

Xem đáp án

Câu 24:

Trong các khẳng định sau, khẳng định nào sai?

A. Phép dời hình là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kì

B. Hai hình được gọi là bằng nhau nếu có phép dời hình biến hình này thành hình kia

C. Phép dời hình biến đường tròn thành đường tròn có cùng bán kính

D. Phép dời hình là phép đồng nhất

Xem đáp án

Đáp án D

Ví dụ phép tịnh tiến theo $\vec{v} \neq \vec{0}$ là một phép dời hình, nhưng không phải là phép đồng nhất.

Câu 25:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAD là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng AD và SC là

A. $\frac{a \sqrt{3}}{21}$

B. $\frac{a \sqrt{21}}{7}$

C. $\frac{2 a}{\sqrt{3}}$

D. $\frac{a \sqrt{3}}{7}$

Xem đáp án

Câu 26:

Ông Minh mua một con lợn đất và ông ta bỏ tiền vào đó như sau: Tháng đầu tiên ông ta bỏ vào đó 6 triệu đồng. Các tháng tiếp theo cứ đầu mỗi tháng ông bỏ thêm vào 1 triệu đồng. Hỏi sau ít nhất bao nhiêu tháng ông ta đủ mua tiền mua một chiếc điện thoại Iphone X giá 30 triệu đồng?

A. 27

B. 24

C. 28

D. 25

Xem đáp án

Đáp án D

Phương thức ông Minh đóng tiền theo quy luật cấp số cộng:

Tháng đầu tiên ông bỏ vào đó 6 triệu đồng, tương ứng với $u_{1} = 6$

Câu 27:

Cho hình chóp tứ giác đều có cạnh đáy bằng a, mặt bên tạo với mặt đáy một góc $60^{0} .$ Diện tích xung quanh của hình nón ngoại tiếp hình chóp là

A. $\frac{{πa}^{2} \sqrt{10}}{4}$

B. $\frac{{πa}^{2} \sqrt{5}}{4}$

C. $\frac{{πa}^{2} \sqrt{10}}{2}$

D. $\frac{{πa}^{2} \sqrt{5}}{2}$

Xem đáp án

Câu 28:

Cho hình lập phương ABCD.A′B′C′D′. Gọi O,O′ lần lượt là tâm của hai hình vuông ABCD và A′B′C′D′. Gọi $V_{1}$ là thể tích của khối trụ tròn xoay có đáy là 2 đường tròn ngoại tiếp hình vuông ABCD và A′B′C′D′, $V_{2}$ là thể tích khối nón tròn xoay đỉnh O và có đáy là đường tròn nội tiếp hình vuông A′B′C′D′. Tỷ số thể tích $\frac{V_{1}}{V_{2}}$ là

A. 6

B. 2

C. 8

D. 4

Xem đáp án

Câu 29:

Cho số phức $z = {(1 + i)}^{5}$ . Điểm biểu diễn số phức z nằm trong góc phần tư nào của hệ tọa độ vuông góc của mặt phẳng phức?

A. Góc phần tư thứ I

B. Góc phần tư thứ II

C. Góc phần tư thứ III

D. Góc phần tư thứ IV

Xem đáp án

Câu 30:

Có 5 bạn học sinh An, Bình, Cường, Dũng, Huệ ngồi vào một dãy ghế hàng ngang, có 5 chỗ ngồi. Tính xác suất để bạn Cường ngồi chính giữa.

A. $\frac{3! 2!}{5!}$

B. $\frac{3!}{5!}$

C. $\frac{2! 2!}{5!}$

D. $\frac{4!}{5!}$

Xem đáp án

Đáp án D

Số cách sắp xếp để bạn Cường ngồi chính giữa chính là số hoán vị của 4 bạn còn lại.

Vậy xác suất cần tính là $\frac{4!}{5!}$

Câu 31:

Cho $_{- 3}^{- 1} f (x) dx = 1,_{3}^{0} f (x) dx = - 2$ . Tính $_{0}^{- 1} f (x) dx +_{- 3}^{3} f (x) dx$

A. -1

B. -3

C. 3

D. 1

Xem đáp án

Đáp án C

Ta có

Câu 32:

Cho $\log_{a} b = 2 .$ Tính $\log_{\frac{a}{b}} (a^{2} b) .$

A. 1

B. $\frac{1}{2}$

C. -6

D. $- \frac{1}{2}$

Xem đáp án

Câu 33:

Cho hình chóp $S . ABC, SA = 8, SA$ vuông góc với đáy. Tam giác ABC vuông tại $A, BC = 7$ . Tính bán kính của mặt cầu ngoại tiếp khối chóp.

A. $\sqrt{113}$

B. $\frac{\sqrt{113}}{4}$

C. $\frac{\sqrt{113}}{3}$

D. $\frac{\sqrt{113}}{2}$

Xem đáp án

Đáp án D

Gọi M là trung điểm của BC. Suy ra M là tâm đường tròn ngoại tiếp tam giác vuông ABC.

Kẻ đường thẳng Δ đi qua M và vuông góc với mặt phẳng (ABC), Δ chính là trục của đường tròn ngoại tiếp đa giác đáy.

Trong mặt phẳng chứa SA và Δ, dựng đường trung trực d của

Câu 34:

Cho cấp số cộng $(u_{n})$ có công sai bằng 3. Hỏi dãy $v_{n} = 2 u_{n} + 3$ có công sai bằng bao nhiêu?

A. 4

B. 2

C. 9

D. 6

Xem đáp án

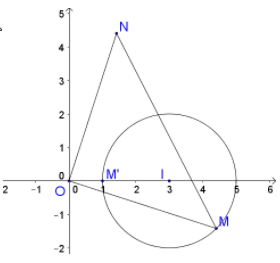
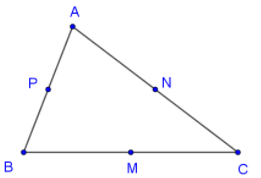
Câu 35:

Trong mặt phẳng, cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm các cạnh BC, CA, AB. Phép tịnh tiến theo vecto $\vec{v} = \frac{1}{2} \vec{BC}$ biến

A. Điểm M thành N

B. Điểm M thành B

C. Điểm M thành P

D. Điểm M thành C

Xem đáp án

Đáp án D

Câu 36:

Cho hàm số $f (x) = \{\begin{cases} ax + 3 khix \geq 1 \\ x^{2} + x - 1 khix < 1 \end{cases}$ để $f (x)$ liên tục trên toàn trục số thì a bằng?

A. 1

B. -2

C. 0

D. -1

Xem đáp án

Câu 37:

Giá trị $\sqrt[7]{3 \sqrt[5]{3 \sqrt[3]{3}}}$ viết dưới dạng lũy thừa với số mũ hữu tỉ là

A. $3^{\frac{17}{105}}$

B. $3^{\frac{4}{105}}$

C. $3^{\frac{1}{105}}$

D. $3^{\frac{19}{105}}$

Xem đáp án

Câu 38:

Xác định $\lim_{x \to {(- 1)}^{-}} \frac{x^{2} + 3 x + 2}{|x + 1|}$

A. $- \infty$

B. -1

C. 1

D. $+ \infty$

Xem đáp án

Câu 39:

Tính tổng $S = 100^{2} - 99^{2} + 98^{2} - 97^{2} + .... + 2^{2} - 1^{2}$

A. 5050

B. 4949

C. 10100

D. 9898

Xem đáp án

Câu 40:

Tập nghiệm của bất phương trình $6^{\log_{6}^{2} x} + x^{\log_{6} x} \leq 12$ có dạng $S = [a; b]$ . Tính $P = a + b .$

A. $\frac{1}{6}$

B. $\frac{6}{37}$

C. 0

D. $\frac{37}{6}$

Xem đáp án

Câu 41:

Trong mặt phẳng phức cho các điểm A, B, C theo thứ tự biểu diễn các số phức $z_{1} = - i; z_{2} = 2 + i; z_{3} = - 1 + i$ . Tìm số phức z biểu diễn điểm D sao cho tứ giác ABCD là hình bình hành.

A. $z = - 3 - i$

B. $z = - 2 - i$

C. $z = - 3$

D. $z = - 1 - 3 i$

Xem đáp án

Câu 42:

Tính diện tích hình phẳng giới hạn bởi các đường ${y=xe}^{x}$ , trục hoành, đường thẳng x=0 và x=1

A. $S = e - 1$

B. $S = e$

C. $S = 1$

D. $S = e + 1$

Xem đáp án

Câu 43:

Ông Minh gửi gói tiết kiệm tích lũy cho con tại một ngân hàng với số tiền tiết kiệm ban đầu là 200 triệu đồng với lãi suất 7%/ năm. Từ năm thứ hai trở đi, mỗi năm ông gửi thêm vào tài khoản với số tiền 20 triệu đồng. Ông không rút lãi định kỳ hàng năm. Biết rằng, lãi suất định kì hàng năm không thay đổi. Hỏi sau 10 năm, số tiền ông Minh nhận về cả gốc lẫn lãi là bao nhiêu? (làm tròn đến 3 chữ số thập phân).

A. 675,126 triệu đồng

B. 710,030 triệu đồng

C. 669,759 triệu đồng

D. 559,632 triệu đồng

Xem đáp án

Đáp án C

Gọi A là số tiền gốc ban đầu, lãi suất r / năm, số tiền gửi thêm là a (triệu đồng).

Sau năm đầu tiên, số tiền cả gốc lẫn lãi mà ông Minh nhận được là: $A (1 + r)$

Sau năm thứ 2, cả gốc và lãi ông nhận được là: $[A (1 + r) + a] (1 + r) = A {(1 + r)}^{2} + a (1 + r)$

Sau năm thứ 3, cả gốc và lãi ông nhận được:

$[A {(1 + r)}^{2} + a (1 + r) + a] (1 + r) = A {(1 + r)}^{3} + a {(1 + r)}^{2} + a (1 + r)$

…

Sau năm thứ n, ông Minh nhận được số tiền:

$A {(1 + r)}^{n} + a {(1 + r)}^{n - 1} + a {(1 + r)}^{n - 2} + . .. + a = A {(1 + r)}^{n} + a . \frac{{(1 + r)}^{n} - 1}{r}$

Thay số: sau 10 năm ông Minh nhận về cả gốc lẫn lãi là

$200 {(1 + 0, 07)}^{10} + 20. \frac{{(1 + 0, 07)}^{10} - 1}{0, 07} = 669, 759$ triệu đồng.

Câu 44:

Một nhà sản xuất cần thiết kế một thùng sơn dạng hình trụ có nắp đậy với dung tích là 20lít. Cần phải thiết kế thùng sơn đó với bán kính nắp đậy là bao nhiêu (cm) để nhà sản xuất tiết kiện được vật liệu nhất?

A. $\frac{100}{\sqrt[3]{π}}$

B. $\sqrt[3]{\frac{10000}{π}}$

C. $\frac{200}{π}$

D. $\frac{200}{\sqrt{π}}$

Xem đáp án

Đáp án B

Đổi 20 lít =20000cm³.

Gọi bán kính nắp đậy của thùng sơn là x (cm), x>3,

chiều cao của thùng sơn là h(cm).

Khi đó thể tích của thùng sơn là

Câu 45:

Trong không gian hệ tọa độ Oxyz cho mặt cầu $(S) x^{2} + y^{2} + z^{2} - 2 x + 2 y - 4 z - 10 = 0$ và mặt phẳng $(P) : 2 x + y - z - 5 = 0 .$ Viết phương trình mặt phẳng (Q) song song với mặt phẳng (P) và cắt mặt cầu (S) theo đường tròn có bán kính bằng một nửa bán kính mặt cầu (S).

A. $(Q_{1}) : 2 x + y - z + 1 + 6 \sqrt{2} = 0$ và $(Q_{2}) : 2 x + y - z + 1 - 6 \sqrt{2} = 0$

B. $(Q_{1}) : 2 x + y - z + 1 + 2 \sqrt{3} = 0$ và $(Q_{2}) : 2 x + y - z + 1 - 2 \sqrt{3} = 0$

C. $(Q_{1}) : 2 x + y - z - 1 + 6 \sqrt{2} = 0$ và $(Q_{2}) : 2 x + y - z - 1 - 6 \sqrt{2} = 0$

D. $(Q_{1}) : 2 x + y - z + 2 \sqrt{3} = 0$ và $(Q_{2}) : 2 x + y - z - 2 \sqrt{3} = 0$

Xem đáp án

Câu 46:

Cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 2 x + 4 y - 2 z - 3 = 0$ cắt hai mặt phẳng $(P) : x - 2 y + z = 0$ và $(Q) : x - z - 2 = 0$ theo các đường tròn giao tuyến với bán kính $r_{1}$ và $r_{2}$ . Khi đó tỉ số $\frac{r_{1}}{r_{2}}$ bằng

A. $\frac{\sqrt{3}}{2}$

B. $\frac{\sqrt{7}}{3}$

C. $\sqrt{\frac{3}{7}}$

D. $\sqrt{\frac{3}{5}}$

Xem đáp án

Câu 47:

Cho hai đường thẳng a, b cố định, song song với nhau và khoảng cách giữa chúng bằng 4. Hai mặt phẳng (P), (Q) thay đổi vuông góc gới nhau lần lượt chứa hai đường thẳng a, b. Gọi d là giao tuyến của (P), (Q). Khẳng định nào sau đây là đúng?

A. d thuộc một mặt trụ cố định có khoảng cách giữa đường sinh và trục bằng 4

B. d thuộc một mặt trụ cố định có khoảng cách giữa đường sinh và trục bằng 22

C. d thuộc một mặt trụ cố định có khoảng cách giữa đường sinh và trục bằng 2

D. d thuộc một mặt nón cố định

Xem đáp án

Câu 48:

Cho hàm số $y = x^{4} - 2 {mx}^{2} - m .$ Với giá trị nào của m thì đồ thị hàm số có ba điểm cực trị đồng thời ba điểm cực trị đó tạo thành một tam giác vuông cân.