50 câu hỏi trắc nghiệm thuộc Tổng hợp đề thi thptqg môn Toán cực hay mới nhất (Đề số 09)

Câu 1:

Cho hai số phức $z_{1} = 1 + i, z_{2} = 2 - 2 i .$ Phần thực và phần ảo của số phức $z_{1} . z_{2}$ tương ứng bằng

A. 4 và 0

B. – 4 và 0

C. 0 và – 4

D. 0 và 4

Xem đáp án

Câu 2:

Cho hàm số $y = x^{3} + {ax}^{2} + bx + 1$ và giả sử A, B là hai điểm cực trị của đồ thị hàm số. Khi đó điều kiện để đường thẳng AB đi qua gốc tọa độ $O (0; 0)$ là

A. ab = 2

B. ab = 9

C. a = 0

D. a = 3b

Xem đáp án

Câu 3:

Cho hình chóp SABCD có $SA = SB = SC = AB = AC = a;$ $BC = a \sqrt{2}$ . Tính góc giữa 2 đường thẳng AB và SC.

A. $60^{0}$ x

B. $90^{0}$

C. $120^{0}$

D. $45^{0}$

Xem đáp án

Câu 4:

Có bao nhiêu điểm M trên đường thẳng $d : \{\begin{cases} x = 1 - t \\ y = 1 + t \\ z = 2 t \end{cases}$ mà $AM = \sqrt{1} 0$ với $A (0; 1; - 1) ?$

A. 3

B. 0

C. 2

D. 1

Xem đáp án

Câu 5:

Trong mặt phẳng Oxy, gọi các điểm M, N lần lượt là điểm biểu diễn số phức $z_{1} = 2 - i, z_{2} = 1 + 4 i .$ Gọi G là trọng tâm của tam giác OMN, với O là gốc tọa độ. Hỏi G là điểm biểu diễn của số phức nào sau đây?

A. $z_{3} = i$

B. $z_{3} = 1 + i$

C. $z_{3} = 1$

D. $z_{3} = 1 - i$

Xem đáp án

Câu 6:

Cho đường tròn (C) có tâm I(1;2) và bán kính $R = 3$ . Phép tịnh tiến theo vecto $\vec{v} (2; 0)$ biến (C) thành (C’) có phương trình là

A. ${(x - 3)}^{2} + {(y - 2)}^{2} = 9$

B. ${(x - 1)}^{2} + {(y + 2)}^{2} = 9$

C. ${(x + 3)}^{2} + {(y + 2)}^{2} = 9$

D. ${(x - 3)}^{2} + {(y - 2)}^{2} = 3$

Xem đáp án

Câu 7:

Tìm tập các định của hàm số $y = {(x - 1)}^{π} + {(x^{2} - 4)}^{e}$ .

A. $[2; + \infty)$

B. $[2; + \infty]$

C. $(2; + \infty)$

D. $ℝ$

Xem đáp án

Đáp án A

Hàm lũy thừa với số mũ không nguyên, có tập xác định là tập các số thực dương.

Vậy ta có

Câu 8:

Tìm m để phương trình $x^{3} - 3 x^{2} - 9 x + m = 0$ (1) có ba nghiệm phân biệt lập thành cấp số cộng.

A. m = 10

B. m = 11

C. m = 12

D. m = 9

Xem đáp án

Đáp án A

Điều kiện cần: Giả sử phương trình có ba nghiệm phân biệt lập thành cấp số cộng, khi đó

Câu 9:

Trong không gian với hệ trục tọa độ Oxyz, cho điểm $G (1; 2; 3)$ . Mặt phẳng $(α)$ đi qua G cắt Ox,Oy,Oz lần lượt tại A, B, C sao cho G là trọng tâm của tam giác ABC. Viết phương trình mặt phẳng $(α)$ .

A. $(α) : \frac{x}{3} + \frac{y}{6} + \frac{z}{9} = 1$

B. $(α) : \frac{x}{2} + \frac{y}{4} + \frac{z}{6} = 1$

C. $(α) : \frac{x}{3} + \frac{y}{2} + \frac{z}{1} = 1$

D. $(α) : \frac{x}{1} + \frac{y}{2} + \frac{z}{3} = 1$

Xem đáp án

Câu 10:

Phương trình đường tiệm cận xiên của đồ thị hàm số $f (x) = \frac{2 x^{2} - x + 3}{x - 1}$ là

A. $y = 2 x + 1$

B. $y = 2 x - 1$

C. $y = x - 1$

D. $y = - 2 x - 1$

Xem đáp án

Câu 11:

Nguyên hàm của hàm số $f (x) = \cos (2 x - 3)$ là

A. $\int^{} f (x) dx = - \frac{1}{2} \sin (2 x - 3) + C$

B. $\int^{} f (x) dx = 2 \sin (2 x - 3) + C$

C. $\int^{} f (x) dx = \frac{1}{2} \sin (2 x - 3) + C$

D. $\int^{} f (x) dx = - 2 \sin (2 x - 3) + C$

Xem đáp án

Câu 12:

Khối lăng trụ tam giác đều có tất cả các cạnh bằng nhau và có thể tích là $\frac{27 \sqrt{3}}{4}$ thì độ dài các cạnh bằng

A. $\sqrt{3}$

B. 3

C. $\sqrt[3]{3}$

D. $\sqrt[3]{9}$

Xem đáp án

Câu 13:

Tập xác định của hàm số $f (x) = \sqrt{\log_{2} \frac{x^{2} - 3 x + 2}{x + 7}}$ là

A. $D = (- 7; - 1] \cup^{} [5, + \infty)$

B. $D = (- 7; 5]$

C. $D = (5; + \infty)$

D. $D = (- \infty; - 1) \cup^{} (5; + \infty)$

Xem đáp án

Câu 14:

Qua phép đối xứng trục $xx'$ , điểm $M (- 2; 1)$ cho ảnh là điểm nào sau đây?

A. $(1; 2)$

B. $(- 2; - 1)$

C. $(- 1; 2)$

D. $(2; - 1)$

Xem đáp án

Đáp án B

Qua phép đối xứng trục xx', điểm M(2;-1) cho ảnh là (-2;-1)

Câu 15:

Số cách xếp 6 bạn học sinh ngồi vào một chiếc bàn học thẳng gồm 7 chỗ là

A. 720

B. 840

C. 7

D. 5040

Xem đáp án

Đáp án C

Xếp 6 bạn ngồi vào chiếc bàn học thẳng 7 chỗ chính là số cách chọn ra 6 chỗ trong 7 chỗ và có tính thứ tự, do đó có $A_{7}^{6} = 5040$ cách.

Câu 16:

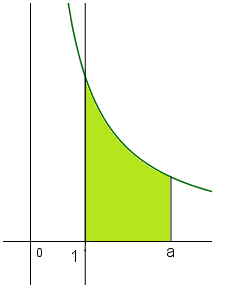
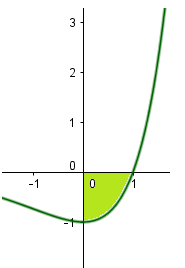
Cho hình phẳng (H) nằm hoàn toàn trong góc phần tư thứ (IV), được giới hạn bởi các đường $y = (x - 1) e^{x}$ , trục hoành, trục tung. Tính thể tích V hình tròn xoay sinh bởi (H) khi quay (H) quanh trục Ox.

A. $- \frac{5 π}{4} + \frac{{πe}^{2}}{4}$

B. $πe + \frac{π}{2}$

C. $π - e$

D. $π + πe$

Xem đáp án

Đáp án C

Hoành độ giao điểm của đồ thị hàm số $y = (x - 1) e^{x}$ với trục hoành là nghiệm của phương trình $(x - 1) e^{x} = 0 \Leftrightarrow x = 1 .$

Câu 17:

Cho hàm số $y = x^{3} - 3 x^{2} + m$ (1). Tìm m để tiếp tuyến của đồ thị (1) tại điểm có hoành độ bằng 1 cắt các trục Ox, Oy lần lượt tại các điểm A, B mà diện tích tam giác OAB bằng $\frac{3}{2}$ .

A. m = 2

B. m = 3 hoặc m = -1

C. m = 4 hoặc m = 2

D. m = 3

Xem đáp án

Câu 18:

Tìm số hạng đầu $u_{1}$ và công bội q của cấp số nhân $(u_{n})$ , biết $\{\begin{cases} u_{4} - u_{2} = 72 \\ u_{5} - u_{3} = 144 \end{cases}$

A. $q = \frac{1}{2}, u_{1} = \frac{1}{12}$

B. $q = 2, u_{1} = 14$

C. $q = \frac{1}{2}, u_{1} = \frac{1}{14}$

D. ${q=2,u}_{1} = 12$

Xem đáp án

Câu 19:

Giá trị của biểu thức $P = \frac{2^{5} . 2^{- 2} + {(\frac{1}{2})}^{- 2} . 2^{2}}{{(0, 5)}^{- 4} . {(0, 25)}^{2}}$ là

A. 16

B. 24

C. 128

D. 32

Xem đáp án

Câu 20:

$\lim_{x \to + \infty} \frac{x - 3}{x + 2}$ bằng

A. 0

B. $+ \infty$

C. $- \frac{3}{2}$

D. 1

Xem đáp án

Câu 21:

Hình vẽ bên giống với đồ thị của hàm số nào nhất trong bốn hàm số được liệt kê ở bốn phương án A,B,C,D dưới đây? Biết rằng hàm số có dạng $f (x) = a x^{3} + b x^{2} + c x + d, (a \neq 0)$

A. $y = x^{3} + 3 x + 2$

B. $y = - x^{3} + 3 x + 2$

C. $y = - x^{3} - 3 x + 2$

D. $y = x^{3} - 3 x + 2$

Xem đáp án

Câu 22:

Xét phương trình $z^{3} = 1$ trên tập số phức. Tập nghiệm của phương trình là

A. $S = \{\frac{- 1 \pm \sqrt{3} i}{2}\}$

B. $S = \{1\}$

C. $S = \{1; \frac{- 1 \pm \sqrt{3} i}{2}\}$

D. $S = \{- 1; \frac{- 1 \pm \sqrt{3}}{2}\}$

Xem đáp án

Câu 23:

Cho hàm số $y = {mx}^{3} + 3 {mx}^{2} + x - 1$ . Tìm m để hàm số đồng biến trên $ℝ$

A. $0 \leq m < \frac{1}{3}$

B. $0 < m \leq \frac{1}{3}$

C. $0 \leq m \leq \frac{1}{3}$

D. m < 0 hoặc $m \geq \frac{1}{3}$

Xem đáp án

Câu 24:

Trong mặt phẳng Oxy, gọi các điểm M, N lần lượt là điểm biểu diễn số phức $z_{1} = 2 - i, z_{2} = 1 + 4 i .$ Gọi G là trọng tâm của tam giác OMN, với O là gốc tọa độ. Hỏi G là điểm biểu diễn của số phức nào sau đây?

A. $z_{3} = i$

B. $z_{3} = i + 1$

C. $z_{3} = 1$

D. $z_{3} = 1 - i$

Xem đáp án

Câu 25:

Hàm số $y = x^{3} - 3 x + 3$ có giá trị cực đại là

A. 7

B. 5

C. -1

D. 1

Xem đáp án

Câu 26:

Số hạng không chứa x trong khai triển ${(\frac{2}{x^{3}} - x^{2})}^{10}$ là

A. 16

B. -16

C. 32

D. -32

Xem đáp án

Câu 27:

Cho hình hộp chữ nhật ABCD.A′B′C′D′ có đáy là hình vuông cạnh a và cạnh bên bằng 3a. Diện tích xung quanh S_xq của hình nón có đỉnh là tâm O của hình vuông A′B′C′D′ và có đáy là hình tròn nội tiếp hình vuông ABCD là

A. $S_{xq} = \frac{\sqrt{13} {πa}^{2}}{4}$

B. $S_{xq} = \frac{\sqrt{37} {πa}^{2}}{12}$

C. $S_{xq} = \frac{\sqrt{13} {πa}^{2}}{12}$

D. $S_{xq} = \frac{\sqrt{37} {πa}^{2}}{4}$

Xem đáp án

Câu 28:

Một người gửi tiền vào ngân hàng theo thể thức lãi kép với lãi suất 12%/năm, lãi được tính theo từng tháng. Hỏi sau bao lâu, số tiền trong tài khoản của người đó gấp 4 lần số tiền ban đầu?

A. 140 tháng

B. 12 năm

C. 120 tháng

D. 136 tháng

Xem đáp án

Đáp án D

Gọi A là số tiền ban đầu mà người đó gửi vào ngân hàng.

Sau 1 tháng số tiền người đó nhận được là $A (1 + r)$

Sau 2 tháng số tiền người đó nhận được là $A {(1 + r)}^{2}$

…

Sau n tháng số tiền người đó nhận được là $A {(1 + r)}^{n}$

Giả sử sau n tháng, số tiền trong tài khoản của người đó gấp n lần số tiền ban đầu. Ta có $4 A = A {(1 + r)}^{n}$

$\Leftrightarrow 4 = {(1 + 0, 01)}^{n}$

$\Leftrightarrow n = \log_{1, 01} 4 \approx 140 .$

Vậy sau 140 tháng thì số tiền của người đó trong tài khoản gấp 4 lần số tiền ban đầu.

Câu 29:

Tìm a để diện tích hình phẳng giới hạn bởi đường cong $y = \frac{3}{x},$ đường thẳng $x = 1$ đường thẳng $x = a (a > 1)$ bằng 3.

A. 3e

B. e

C. 2e

D. $e^{2}$

Xem đáp án

Câu 30:

Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng $(P) : x - 2 y + z - 3 = 0$ và mặt phẳng $(Q) : - 2 x + 4 y - 2 z - 7 = 0 .$ Khẳng định nào sau đây là đúng?

A. $(P) \equiv (Q)$

B. $(P)$ cắt $(Q)$

C. $(P) ⊥ (Q)$

D. $(P) / / (Q)$

Xem đáp án

Câu 31:

Một đề thi có 5 câu được chọn ra từ một ngân hàng câu hỏi có sẵn gồm 100 câu, một học sinh thuộc 80 câu. Tính xác suất để học sinh đó rút ngẫu nhiên được một đề thi có 4 câu đã học thuộc?

A. Đáp án khác

B. $\frac{1}{1075536}$

C. $\frac{1}{3764376}$

D. $\frac{5}{268884}$

Xem đáp án

Câu 32:

Số giao điểm của đồ thị hàm số $y = x^{4} - 3 x^{2} - 1$ và đường thẳng $y = - 2 x - 1$ là

A. 1

B. 4

C. 2

D. 3

Xem đáp án

Câu 33:

Người ta cần đổ một ống thoát nước hình trụ bằng bê tông với chiều cao 100cm, độ dày của thành ống là 10cm và đường kính của ống là 50cm. Lượng bê tông cần phải đổ là

A. $4000 {πcm}^{3}$

B. $0, 04 {πcm}^{3}$

C. $0, 05 {πcm}^{3}$

D. $5000 {πcm}^{3}$

Xem đáp án

Câu 34:

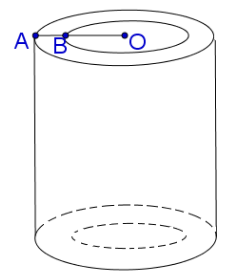
Một hình trụ có tâm các đáy là O,O′. Biết rằng mặt cầu đường kính OO′ tiếp xúc với các mặt đáy của hình trụ tại O,O′ và tiếp xúc với mặt xung quanh của hình trụ đó. Diện tích của mặt cầu này là 8π. Tính diện tích xung quanh của hình trụ đã cho.

A. $16 π$

B. $\frac{8 π}{3}$

C. $8 π$

D. $\frac{16 π}{3}$

Xem đáp án

Đáp án C

Theo bài ra ta có chiều cao của hình trụ bằng đường kính đáy của hình trụ và bằng đường kính của mặt cầu.

Gọi bán kính của mặt cầu là R

Câu 35:

Cho $A (1; 1; - 1), B (3; 1; 2), C (0; 1; - 1)$ và điểm D nằm trên trục Oy và thể tích tứ diện ABCD bằng 1. Tọa độ của D là

A. $D (0; 2; 0)$

B. $D (0; - 2; 0)$

C. $D (0; - 3; 0)$

D. $[\begin{array}{l} D (0; - 1; 0) \\ D (0; 3; 0) \end{array}$

Xem đáp án

Câu 36:

Giá trị lớn nhất của hàm số $y = x + \sqrt{2} cosx$ trên đoạn $[0; \frac{π}{2}]$

A. $\frac{π}{3} + 1$

B. $y_{\max} = \frac{π}{4} + 1$

C. $\sqrt{2}$

D. $y_{\max} = \frac{π}{2}$

Xem đáp án

Câu 37:

Biết hàm số $f (x)$ có đạo hàm $f' (x)$ liên tục trên $ℝ$ và $f (1) = e^{2}, \int_{1}^{\ln 2} f^{'} (x) dx = 4 - e^{2}$ . Tính $f (\ln 2)$

A. $f (\ln 2) = 4 + 2 e^{2} a$

B. $f (\ln 2) = 4$

C. $f (\ln 2) = 4 - 2 e^{2}$

D. $f (\ln 2) = 4 - e^{2}$

Xem đáp án

Câu 38:

Cho đường thẳng $d : \frac{x + 1}{2} = \frac{y - 1}{1} = \frac{z - 2}{1}$ . Hình chiếu vuông góc của d lên mặt phẳng (Oxy) là đường thẳng

A. $d^{'} : \{\begin{cases} x = - 1 + 2 t \\ y = t \\ z = 0 \end{cases}$

B. $d^{'} : \{\begin{cases} x = - 1 + t \\ y = 1 + t \\ z = 0 \end{cases}$

C. $d^{'} : \{\begin{cases} x = - 1 + 2 t \\ y = 1 + t \\ z = 0 \end{cases}$

D. $d^{'} : \{\begin{cases} x = 2 t \\ y = t \\ z = 0 \end{cases}$

Xem đáp án

Câu 39:

Khi x thay đổi trong khoảng $[\frac{2 π}{3}; \frac{7 π}{3})$ thì hàm $y = cosx$ lấy mọi giá trị thuộc khoảng

A. $[0; \frac{1}{2}]$

B. $[0; 1]$

C. $[\frac{1}{2}; 1]$

D. $[0; \frac{1}{2})$

Xem đáp án

Câu 40:

Tìm các khoảng và nửa khoảng (lớn nhất) mà trên đó hàm số $f (x) = \frac{x}{x^{2} + x - 6}$ liên tục.

A. $(- \infty; - 3)$ và $[2; + \infty)$

B. $(- \infty; - 3)$ và $(2; + \infty)$

C. $(- \infty; - 3]$ và $(2; + \infty)$

D. $(- \infty; - 3), (- 3; 2)$ và $(2; + \infty)$

Xem đáp án

Câu 41:

Số điểm biểu diễn nghiệm của phương trình $1 + cosx + \cos 2 x + \cos 3 x = 0$ trên đường tròn lượng giác là

A. 5

B. 3

C. 4

D. 6

Xem đáp án

Câu 42:

Với m bằng bao nhiêu thì phương trình ${\log_{2}}^{2} x + \log_{\frac{1}{2}} x^{2} - 3 = m (\log_{4} x^{2} - 3)$ có nghiệm $x > 32$

A. 6

B. 5

C. 4

D. 7

Xem đáp án

Đáp án A

Câu 43:

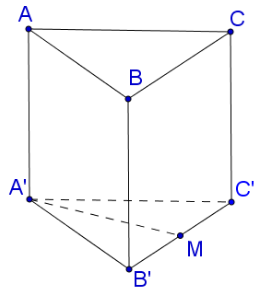
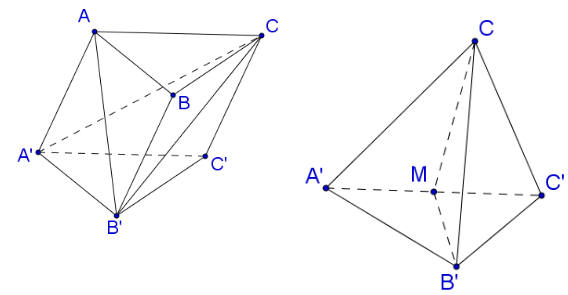
Cho lăng trụ ABCA′B′C′, đáy là tam giác đều cạnh bằng a, tứ giác ABB′A′ là hình thoi, $\hat{A^{'} AC} = 60^{o}, B^{'} C = \frac{a \sqrt{3}}{2}$ . Tính thể tích lăng trụ ABCA′B′C′.

A. $\frac{\sqrt{3} a^{3}}{4}$

B. $\frac{3 \sqrt{3} a^{3}}{4}$

C. $\frac{3 \sqrt{3} a^{3}}{16}$

D. $\frac{\sqrt{3} a^{3}}{16}$

Xem đáp án

Đáp án A

Dễ dàng tính được các cạnh của tứ diện CA′B′C′:

$A^{'} C = A^{'} C^{'} = {CC}^{'} = B^{'} C^{'} = A^{'} B^{'} = a .$

Câu 44:

Cho $F (x)$ là một nguyên hàm của hàm số $f (x) = x \sqrt{x + 1}$ . Tìm $F (x)$ biết $F (0) = 0$

A. $F (x) = \frac{2}{5} \sqrt{{(x + 1)}^{5}} - \frac{2}{3} \sqrt{{(x + 1)}^{3}} + \frac{4}{15}$

B. $F (x) = \frac{1}{5} \sqrt{{(x + 1)}^{5}} - \frac{1}{3} \sqrt{{(x + 1)}^{3}} + \frac{2}{15}$

C. $F (x) = \frac{1}{5} \sqrt{{(x + 1)}^{3}} - \frac{7}{15} \sqrt{x + 1} + \frac{4}{15}$

D. $F (x) = \frac{2}{5} \sqrt{{(x + 1)}^{3}} - \frac{2}{3} \sqrt{x + 1} + \frac{4}{15}$

Xem đáp án

Câu 45:

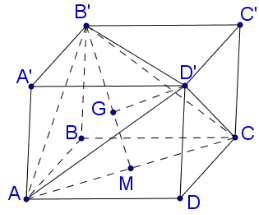
Cho ABCD.A′B′C′D′ là hình lập phương cạnh 2a. Tính thể tích khối tứ diện ACD′B′ là

A. $\frac{8 a^{3}}{3}$

B. $\frac{4 a^{3}}{3}$

C. $\frac{2 a^{3}}{3}$

D. $\frac{8 a^{3}}{9}$

Xem đáp án

Đáp án C

Nhận thấy chóp ACD′B′ có tất cả các

cạnh bằng nhau và bằng $2 \sqrt{2} a$

Gọi M là trung điểm của AC, G là

trọng tâm của tam giác AB′C′.

Chóp ACD′B′ nhận D′G là đường cao.

Xét tam giác AB′C′ có

Câu 46:

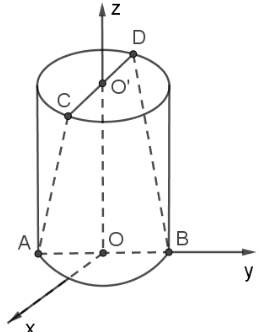
Có một cái hồ rộng 50m, dài 200m. Một vận động viên chạy phối hợp với bơi (bắt buộc cả hai) cần đi từ góc này qua góc đối diện bằng cách cả chạy và bơi (như hình vẽ). Hỏi rằng sau khi chạy được bao xa (quãng đường x) thì nên nhay xuống bơi để đến đích nhanh nhất? Biết rằng vận tốc bơi là 1,5m/s và vận tốc chạy là 4,5m/s.

A. $x \approx 197, 5 m$

B. $x \approx 152, 3 m$

C. $x \approx 182, 3 m$

D. $x \approx 183, 3 m$

Xem đáp án

Đáp án C

Gọi quãng đường vận động viên chạy trên bờ là x (m)

Khi đó quãng đường vận động viên đó bơi dưới nước sẽ là $\sqrt{50^{2} + {(200 - x)}^{2}}$ (m)

Thời gian cho cả quãng đường đi (cả trên bờ và dưới nước) là

Câu 47:

Nếu $a = \log_{6} 2$ thì

A. $\log_{9} 6 = \frac{1}{3 (a - 1)}$

B. $\log_{9} 6 = \frac{1}{2 (a - 1)}$

C. $\log_{9} 6 = \frac{1}{3 (1 - a)}$

D. $\log_{9} 6 = \frac{1}{2 (1 - a)}$

Xem đáp án

Câu 48:

Có 12 cái kẹo giống hệt nhau. Có bao nhiêu cách chia số kẹo đó cho 5 em trong lớp sao cho em nào cũng có kẹo?

A. 7920

B. 330

C. 1650

D. 792

Xem đáp án

Đáp án C

Để đảm bảo em nào cũng có kẹo, ta chia trước cho mỗi em 1 cái. Như vậy còn 7 cái kẹo chia cho 5 em (có thể có em không nhận được cái nào, trừ 1 cái ban đầu được chia).

Đặt theo hàng ngang 7 cái kẹo. Để chia thành 5 nhóm, ta cần đặt 4 vách ngăn.

Bài toán trở thành: có 11 vị trí (7 kẹo, 4 vách ngăn), chọn 4 vị trí đặt vách ngăn. Có $C_{11}^{4} = 330$ cách.

Câu 49:

Tổng các nghiệm của phương trình $4^{x^{2} - 3 x + 2} + 4^{x^{2} + 6 x + 5} = 4^{2 x^{2} + 3 x + 7} + 1$ bằng bao nhiêu?

A. 2

B. 3

C. -3

D. -2

Xem đáp án

Câu 50:

Cho hình trụ có các đường tròn đáy là (O) và (O’), bán kính đáy bằng 1 chiều cao bằng 2. AB, CD lần lượt là đường kính của đường tròn đáy (O) và (O’) sao cho AB vuông góc CD. Tính cosin góc giữa hai đường thẳng AC và BD.

A. $\frac{2}{3}$

B. $\frac{1}{2}$

C. $\frac{\sqrt{3}}{2}$

D. $\frac{1}{3}$

Xem đáp án