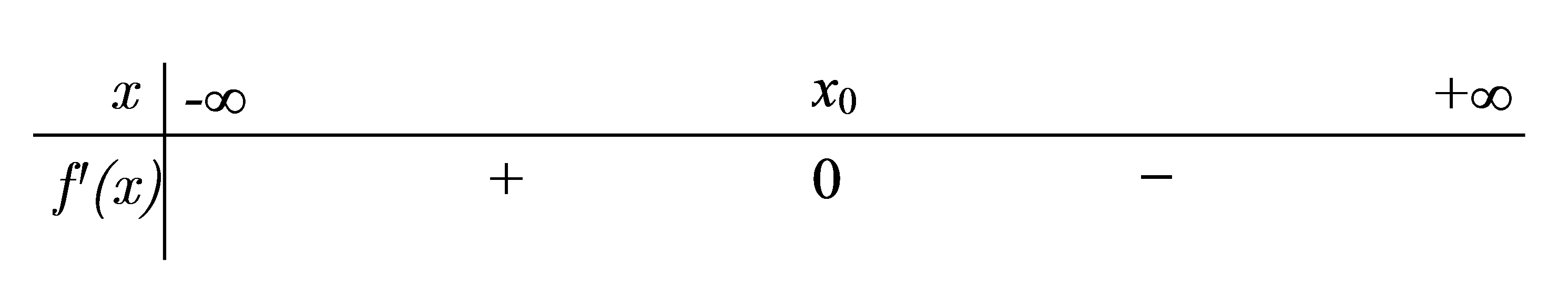50 câu hỏi trắc nghiệm thuộc Tổng hợp 20 đề thi thử THPTQG môn Toán cực hay có đáp án (đề 1)

Câu 1:

Cho hình lập phương $A B C D . E F G H$ có các cạnh a, khi đó $\vec{A B} . \vec{E G}$ bằng

A. $a^{2}$

B. $a^{2} \sqrt{2}$

C. $\frac{a^{2} \sqrt{2}}{2}$

D. $a^{2} \sqrt{3}$

Xem đáp án

Đáp án là A.

Ta có:

$\vec{A B} . \vec{E G} = A B . E G . \cos (\hat{\vec{A B}; \vec{E G}}) = A B . A C . \cos \hat{B A C} = a^{2} \sqrt{2} . \frac{\sqrt{2}}{2} = a^{2} .$

Câu 2:

Phương trình $2 \cos^{2} x + \cos x - 3 = 0$ có nghiệm là

A. $k π$

B. $\frac{π}{2} + k 2 π$

C. $\frac{π}{2} + k π$

D. $k 2 π$

Xem đáp án

Đáp án là D

Ta có:

$2 \cos^{2} x + \cos x - 3 = 0 \Leftrightarrow [\begin{array}{l} \cos x = 1 \Leftrightarrow x = k 2 π, (k \in ℤ) \\ \cos x = \frac{- 3}{2} (p t v n) \end{array}$

Câu 3:

Từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 có thể lập được bao nhiêu số tự nhiên có 5 chữ số đôi một khác nhau sao cho có đúng 3 chữ số chẵn và 2 chữ số lẻ?

A. 2448

B. 3600

C. 2324

D. 2592

Xem đáp án

Đáp án là A.

Gọi số cần lập có dạng: $\bar{a_{1} a_{2} a_{3} a_{4} a_{5}}$

• Chọn 2 số lẻ thuộc nhóm $\{1; 3; 5; 7\} \Rightarrow C_{4}^{2}$

• Chọn 3 số chẳn trong nhóm $\{0; 2; 4; 6\} \Rightarrow C_{4}^{3}$

• Hoán vị 2 nhóm trên có 5! cách

* Các số có số $a_{1} = 0$

• Chọn 2 số lẻ thuộc nhóm $\{1; 3; 5; 7\} \Rightarrow C_{4}^{2}$

• Chọn 2 số chẳn trong nhóm $\{0; 2; 4; 6\} \Rightarrow C_{3}^{2}$

• Hoán vị 2 nhóm trên có 4! cách

Vậy các số cần tìm: $C_{4}^{2} . C_{4}^{3} .5! - C_{4}^{2} . C_{3}^{2} .4! = 2448$ số

Câu 4:

Xếp ngẫu nhiên 3 người đàn ông, hai người đàn bà và một đứa bé vào ngồi 6 cái ghế xếp thành hàng ngang. Xác suất sao cho đứa bé ngồi giữa hai người đàn bà là

A. $\frac{1}{6}$

B. $\frac{1}{5}$

C. $\frac{1}{30}$

D. $\frac{1}{15}$

Xem đáp án

Đáp án là D.

• Số phần tử không gian mẫu $n (Ω) = 6!$

• Gọi biến cố A" đứa bé ngồi giữa hai người đàn bà".

+ Xếp 2 người đàn bà ngồi 2 bên đứa bé có: 2! cách

+ Xem 2 người đàn bà và đứa bé là 1 vị trí sắp xếp với 3 người đàn ông còn lại có: 4! cách

+ Số phần tử của $A : n (A) = 2! .4!$

Xác suất cần tìm $P (A) = \frac{2! .4!}{6!} = \frac{1}{15} .$

Câu 5:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, $S A = a \sqrt{3}$ và vuông góc với đáy. Góc giữa đường thẳng SD và mặt phẳng (ABCD) bằng

A. $60 °$

B. $45 °$

C. $30 °$

D. $a c r \sin \frac{\sqrt{3}}{5}$

Xem đáp án

Đáp án là A

Ta có: $(\hat{S D; (A B C D)}) = (\hat{S D; (A D)}) = \hat{S D A} .$

Trong tam giác SAD có:

$\tan \hat{S D A} = \frac{S A}{A D} = \frac{a \sqrt{3}}{a} = \sqrt{3} \Rightarrow \hat{S D A} = 60^{0} .$

Câu 6:

Cho các hàm số sau:

$y = \frac{1}{x - 3} (I); y = x^{3} - 3 x + 2 (I I); y = - x^{4} + 2 x^{2} (I I I) .$

Trong các hàm số đã cho hàm không có cực trị là:

A. Chỉ (II)

B. Chỉ (III)

C. Chỉ (I)

D. (I) và (II)

Xem đáp án

Đáp án là C

• Hàm số (I) là hàm nhất biến nên không có cực trị.

• Hàm số (II) có phương trình y'=2 có 2 nghiệm phân biệt nên có 2 cực trị.

Hàm số (III) có a.b=-2<0 nên có 3 cực trị.

Câu 7:

Một công ty muốn làm một đường ống dẫn dầu từ một kho A ở trên bờ đến một vị trí B trên một hòn đảo. Hòn đảo cách bờ biển 6 km. Gọi C là điểm trên bờ sao cho BC vuông góc với bờ biển. Khoảng cách từ A đến C là 9 km. Người ta cần xác định một vị trí D trên AC để lắp ống dẫn theo đường gấp khúc ADB. Để số tiền chi phí thấp nhất mà công ty phải thì khoảng cách từ A đến D là bao nhiêu km, biết rằng chi phí để hoàn thành mỗi km đường ống trên bờ là 100 triệu đồng và dưới nước là 260 triệu đồng.

A. 8 km

B. 5 km

C. 7,5 km

D. 6,5 km

Xem đáp án

Đáp án là D.

Đặt $C D = x, x \in [0; 9] .$ Ta có $B D = \sqrt{x^{2} + 36}$

Chi phí xây dựng đường ống $f (x) = 100 (9 - x) + 260 \sqrt{x^{2} + 36}$

Ta có:

$f^{'} (x) = - 100 + \frac{260 x}{\sqrt{x^{2} + 36}}, c h o f^{'} (x) = 0 \Leftrightarrow 5 \sqrt{x^{2} + 36} = 13 x \Leftrightarrow x = \frac{5}{2}$

$f (0) = 2460; f (\frac{5}{2}) = 2340; f (9) \approx 2812, 33$

Chi phí thấp nhất $x = \frac{5}{2} .$ Khoảng cách từ A đến D là: 6,5km

Câu 8:

Tìm m C=2.Với $C = \lim_{x \to 1} \frac{x^{2} - m x + m - 1}{x^{2} - 1}$ để:

A. m=2

B. m= -2

C. m=1

D. m= -1

Xem đáp án

Đáp án là B

Ta có:

$C = \lim_{x \to 1} \frac{(x - 1) (x + 1) - m (x - 1)}{(x - 1) (x + 1)} = \lim_{x \to 1} \frac{x + 1 - m}{x + 1} = \frac{2 - m}{2}$

mà $C = 2 \Rightarrow m = - 2.$

Câu 9:

Từ các chữ số 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên có ba chữ số ?

A. 261

B. 120

C. 102

D. 216

Xem đáp án

Đáp án là D

Gọi số cần lập có dạng $\bar{a b c}$

• a có 6 cách chọn; b có 6 cách chọn; c có 6 cách chọn.

• Vậy có 6.6.6=216 số.

Câu 10:

Phương trình $\sin 2 x + \cos x = 0$ có tổng các nghiệm trong khoảng $(0; 2 π)$ bằng

A. $2 π$

B. $3 π$

C. $5 π$

D. $6 π$

Xem đáp án

Đáp án là C.

$p t \Leftrightarrow \cos x (2 \sin x + 1) = 0 \Leftrightarrow [\begin{array}{l} \cos x = 0 \\ \sin x = \frac{- 1}{2} \end{array} \Leftrightarrow [\begin{array}{l} x = \frac{π}{2} + k π \\ x = \frac{- π}{6} + k 2 π \\ x = \frac{7 π}{6} + k 2 π \end{array}; (k \in ℤ)$

$x \in (0; 2 π) \Rightarrow x \in \{\frac{π}{2}; \frac{3 π}{2}; \frac{- π}{6}; \frac{7 π}{6}\}$ .

Tổng các nghiệm $5 π$

Câu 11:

Hàm số $y = x^{3} + 3 x^{2} - 21 x - 1$ có 2 điểm cực trị là $x_{1}, x_{2}$ thì tích $x_{1} . x_{2}$ bằng

A. –2

B. –7

C. 2

D. 7

Xem đáp án

Đáp án là B

Ta có $y^{'} = 3 x^{2} + 6 x - 21$ .

Hàm số có 2 cực trị $x_{1}; x_{2} \Rightarrow x_{1} . x_{2} = \frac{c}{a} = - 7.$

Câu 12:

Cho hàm số $y = a x^{3} + b x^{2} + c x + d$ có đồ thị như hình bên. Mệnh đề nào dưới đây là đúng ?

A. $a > 0, b < 0, c < 0, d > 0$

B. $a < 0, b < 0, c > 0, d < 0$

C. $a < 0, b > 0, c > 0, d < 0$

D. $a < 0, b > 0, c < 0, d < 0$

Xem đáp án

Đáp án là C

• $y^{'} = 3 a x^{2} + 2 b x + c$

• Từ đồ thị ta có a<0 mà $x_{C D} + x_{C T} = - \frac{2 b}{3 a} > 0 \Rightarrow b > 0$

Mặt khác: $x_{C D} . x_{C T} = \frac{c}{3 a} < 0 \Rightarrow c > 0.$

Câu 13:

Các khoảng đồng biến của hàm số $y = x^{4} - 8 x^{2} - 4$ là

A. $(- 2; 0)$ và $(0; 2)$

B. $(- \infty; - 2)$ và $(2; + \infty)$

C. $(- \infty; - 2)$ và $(0; 2)$

D. $(- 2; 0)$ và $(2; + \infty)$

Xem đáp án

Đáp án là D.

• $y^{'} = 4 x^{3} - 16 x = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ x = \pm 2 \end{array}$

• Xét dấu y'.

Câu 14:

Một học sinh khảo sát sự biến thiên của hàm số như sau:

I. Tập xác định: $D = ℝ$

II. Sự biến thiên: $y' = x^{2} - x - 2; y' = 0 \Leftrightarrow [\begin{array}{l} x = - 1 \\ x = 2 \end{array}$

$\lim_{x \to - \infty} y = - \infty; \lim_{x \to + \infty} y = + \infty$

III. Bảng biến thiên:

IV. Vậy hàm số đồng biến trên nghịch biến trên khoảng $(- \infty; - 1) \cup (2; + \infty)$ , nghịch biến trên khoảng $(- 1; 2)$

Lời giải trên sai từ bước nào?

A. Bước IV

B. Bước I

C. Bước II

D. Bước III

Xem đáp án

Đáp án là D.

• Sai ở bước III (bảng biến thiên)

Câu 15:

Đạo hàm của hàm số $y = \frac{2 - x^{2} + 3 x^{3}}{3}$ tại $x_{0} = 1$ bằng

A. $- \frac{8}{3}$

B. $\frac{7}{3}$

C. $\frac{8}{3}$

D. $\frac{10}{3}$

Xem đáp án

Đáp án là B

$y^{'} = 3 x^{2} - \frac{2}{3} x \Rightarrow y^{'} (1) = \frac{7}{3} .$

Câu 16:

Cho chuyển động thẳng xác định bởi phương trình $s = \frac{1}{2} (t^{4} + 3 t^{2})$ , t được tính bằng giây, s được tính bằng m. Vận tốc của chuyển động tại t=4( giây) bằng

A. 0 m/s

B. 200m/s

C. 150m/s

D. 140m/s

Xem đáp án

Đáp án là D.

• $v = s^{'} = 2 t^{3} + 3 t \Rightarrow v (4) = 140 m / s .$

Câu 17:

Khối chóp S.ABCD có SA vuông góc với (ABC), đáy ABC là tam giác vuông tại B với SB=2a, BC=a và thể tích khối chóp là $a^{3}$ . Khoảng cách từ A đến (SBC) bằng

A. $\frac{a \sqrt{3}}{4}$

B. $6 a$

C. $\frac{3 a}{2}$

D. $3 a$

Xem đáp án

Đáp án là D.

$S_{Δ S B C} = \frac{1}{2} S B . B C = \frac{1}{2} 2 a . a = a^{2} .$

Gọi $h = d (A; (S B C)) \Rightarrow h = \frac{3 V_{S . A B C}}{S_{S B C}} = \frac{3 a^{3}}{a^{2}} = 3 a .$

Câu 18:

Cho khối chóp S.ABCD có thể tích bằng $a^{3}$ . Mặt bên SAB là tam giác đều cạnh a và đáy ABCD là hình bình hành. Khoảng cách giữa SA và CD bằng

A. $\frac{2 a}{\sqrt{3}}$

B. $a \sqrt{3}$

C. $\frac{a}{2}$

D. $2 \sqrt{3} a$

Xem đáp án

Đáp án là D.

• Ta có:

$\{\begin{cases} C D / / A B \\ A B \subset (S A B) \end{cases} \Rightarrow C D / / (S A B) \Rightarrow d (S A; C D) = d (C D; (S A B)) = d (C; (S C D))$

• Gọi $h = d (C; (S A B)) \Rightarrow h = \frac{3 V_{S . A B C}}{S_{Δ S A B}} = \frac{\frac{3}{2} a^{3}}{a^{2} \frac{\sqrt{3}}{4}} = 2 a \sqrt{3}$

Câu 19:

Khẳng định nào sau đây là đúng?

A. Hàm số $y = \tan x$ nghịch biến trên khoảng $(0; \frac{π}{2})$

B. Hàm số $y = \sin x$ đồng biến trên khoảng $(0; π)$

C. Hàm số $y = \cot x$ nghịch biến trên khoảng $(0; π)$

D. Hàm số $y = \cos x$ đồng biến trên khoảng $(0; π)$

Xem đáp án

Đáp án là C.

• Xét A: $y^{'} = \frac{1}{\cos^{2} x} > 0, \forall x \in (0; \frac{π}{2})$ . Do đó loại A.

• Làm tương tự chọn C.

Câu 20:

Hàm số $y = \frac{m x + 1}{x + m}$ đồng biến trên khoảng $(1; + \infty)$ khi

A. $- 1 < m < 1$

B. $m > 1$

C. $m \in ℝ \ [- 1; 1]$

D. $m \geq 1$

Xem đáp án

Đáp án là B.

• Hàm số đồng biến trên $(1; + \infty)$ khi và chỉ khi:

$\{\begin{cases} y^{'} > 0, \forall x \in (1; + \infty) \\ - m \notin (1; + \infty) \end{cases} \Leftrightarrow \{\begin{cases} m^{2} - 1 > 0 \\ - m \leq 1 \end{cases} \Leftrightarrow \{\begin{cases} [\begin{array}{l} m < - 1 \\ m > 1 \end{array} \\ m \geq - 1 \end{cases} \Leftrightarrow m > 1.$

Câu 21:

Cho khai triển nhị thức Newton của ${(2 - 3 x)}^{2 n}$ , biết rằng n là số nguyên dương thỏa mãn $C_{2 n + 1}^{1} + C_{2 n + 1}^{3} + C_{2 n + 1}^{5} + ... + C_{2 n + 1}^{2 n + 1} = 1024.$ .

Hệ số của $x^{7}$ bằng

A. -2099520

B. -414720

C. 2099520

D. 414720

Xem đáp án

Đáp án là A

• Xét khai triển:

${(x + 1)}^{2 n + 1} = C_{2 n + 1}^{0} x^{2 n + 1} + C_{2 n + 1}^{1} x^{2 n} + ... + C_{2 n + 1}^{2 n + 1}$ .

Cho $x = 1$ , ta được: $2^{2 n + 1} = C_{2 n + 1}^{0} + C_{2 n + 1}^{1} + ... + C_{2 n + 1}^{2 n + 1}$ . (1)

Cho $x = - 1$ , ta được: $0 = - C_{2 n + 1}^{0} + C_{2 n + 1}^{1} - ... + C_{2 n + 1}^{2 n + 1}$ . (2)

Cộng (1) và (2) vế theo vế, ta được:

$2^{2 n + 1} = 2 (C_{2 n + 1}^{1} + C_{2 n + 1}^{3} + ... + C_{2 n + 1}^{2 n + 1}) \Leftrightarrow 2^{2 n + 1} = 2.1024 \Leftrightarrow n = 5$

• Xét: ${(2 - 3 x)}^{10} = \sum_{0}^{10} C_{10}^{k} 2^{10 - k} . {(- 3 x)}^{k} = \sum_{0}^{10} {(- 3)}^{k} {.2}^{10 - k} . C_{10}^{k} . x^{k}$

Hệ số của $x^{7}$ là: ${(- 3)}^{7} {.2}^{3} . C_{10}^{7} = - 2099520.$

Câu 22:

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = x^{3} + x^{2} - 5 x$ trên đoạn $[0; 2]$ lần lượt là

A. 1;0

B. 2;-3

C. 3;1

D. 2;1

Xem đáp án

Đáp án là B.

• Ta có: $y^{'} = 3 x^{2} + 2 x - 5, c h o y^{'} = 0 \Leftrightarrow [\begin{array}{l} x = 1 \in [0; 2] \\ x = \frac{- 5}{3} \notin [0; 2] \end{array}$

• $y (0) = 0; y (2) = 2; y (1) = - 3$

Câu 23:

Hàm số nào sau đây có đồ thị như hình vẽ:

A. $y = \frac{x}{x - 1}$

B. $y = \frac{- x}{x - 1}$

C. $y = \frac{x}{x + 1}$

D. $y = \frac{x - 1}{x}$

Xem đáp án

Đáp án là A.

Từ đồ thị ta thấy x=1 và y=1 lần lượt là tiệm cận đứng và tiệm cận ngang nên chọn A.

Câu 24:

Giá trị cực đại của hàm số $y = x^{3} - 3 x^{2} - 9 x + 2$ là

A. -1

B. 7

C. 11

D. 3

Xem đáp án

Đáp án là B

• $y^{'} = 3 x^{2} - 6 x - 9, c h o y^{'} = 0 \Leftrightarrow [\begin{array}{l} x = - 1 \\ x = 3 \end{array}$

• BBT:

Từ BBT, suy ra: $y_{C D} = 7$

Câu 25:

Cho hàm số $y = x^{3} - 3 x^{2} + 2 (C)$ . Phương trình tiếp tuyến có hệ số góc nhỏ nhất của $(C)$ là:

A. $y = - 3 x + 3$

B. $y = 0$

C. $y = - 5 x + 10$

D. $y = - 3 x - 3$

Xem đáp án

Đáp án là A.

• Gọi $M (x_{0}; y_{0}) \in (C)$ là toạ độ tiếp điểm.

• Ta có: $y^{'} (x_{0}) = 3 x_{0}^{2} - 6 x_{0} = 3 {(x_{0} - 1)}^{2} - 3 \geq - 3.$

Dấu "=" xẩy ra khi và chỉ khi $x_{0} = 1$ .

Tiếp tuyến có hệ số góc nhỏ nhất khi $x_{0} = 1 \Rightarrow y_{0} = 0$

• Phương trình tiếp tuyến cần tìm: $y = - 3 x + 3$

Câu 26:

Tất cả các giá trị của m để hương trình $\cos x - m = 0$ vô nghiệm là

A. $- 1 \leq m \leq 1$

B. $m > 1$

C. $[\begin{array}{l} m < - 1 \\ m > 1 \end{array}$

D. $m < - 1$

Xem đáp án

Đáp án là C

phương trình đã cho vô nghiệm khi $|m| > 1$

Câu 27:

Với giá trị nào của m thì hàm số $y = x^{3} - 3 m x^{2} + 3 (m^{2} - 1) + m$ đạt cực đại tại x=1

A. $m = 1$

B. $m = - 1$

C. $m = 2$

D. $m = - 2$

Xem đáp án

Đáp án là C.

• $y^{'} = 3 x^{2} - 6 m x + 3 (m^{2} - 1); {y^{'}}^{'} = 6 x - 6 m$

• Hàm số đạt cực đại tại $x = 1$ thì:

$\{\begin{cases} y^{'} (1) = 0 \\ {y^{'}}^{'} (1) < 0 \end{cases} \Leftrightarrow \{\begin{cases} 3 m^{2} - 6 m = 0 \\ 6 - 6 m < 0 \end{cases} \Leftrightarrow \{\begin{cases} m = 0 v m = 2 \\ m > 1 \end{cases} \Rightarrow m = 2.$

Câu 28:

Khối đa diện nào dưới đây có công thức tính thể tích là $V = \frac{1}{3} B . h$ ( với B là điện tích đáy; h là chiều cao).

A. Khối chóp

B. Khối lăng trụ

C. Khối lập phương

D. Khối hộp chữ nhật

Xem đáp án

Đáp án là A

Câu 29:

Giá trị của $\lim (2 n + 1)$ bằng

A. 0

B. 1

C. $+ \infty$

D. $- \infty$

Xem đáp án

Đáp án là C

$\lim (2 n + 1) = + \infty$

Câu 30:

Hình vẽ sau là đồ thị của hàm số nào?

A. $y = - x^{3} - 3 x^{2} - 3 x - 1$

B. $y = x^{3} - 3 x^{2} + 3 x + 1$

C. $y = + x^{3} + 3 x^{2} + 3 x + 1$

D. $y = x^{3} + 3 x^{2} + 9 x + 1$

Xem đáp án

Đáp án là C

Từ đồ thị, ta có $\{\begin{cases} a > 0 \\ x = - 1 \Rightarrow y = 0 \end{cases}$ .

Câu 31:

Cho $n \in ℕ^{*}$ dãy $(u_{n})$ là một cấp số cộng với $u_{2} = 5$ và công sai $d = 3$ . Khi đó $u_{81}$ bằng

A. 239

B. 245

C. 242

D. 248

Xem đáp án

Đáp án là C

$u_{1} = u_{2} - d = 2; u_{81} = u_{1} + 80 d = 242.$

Câu 32:

Số đường tiệm cận của đồ thị hàm số $y = \frac{x^{2} - 3 x + 2}{4 - x^{2}}$ là

A. 3

B. 2

C. 1

D. 4

Xem đáp án

Đáp án là B

Hàm số được viết lại: $y = \frac{(x - 1) (x - 2)}{(2 - x) (2 + x)} = \frac{1 - x}{x + 2} .$

Dễ thấy đồ thị hàm số có tiệm cận đứng và tiệm cận ngang lần lượt là: $x = - 2; y = - 1$

Câu 33:

Đồ thị hàm số $y = \frac{2 x + 1}{- x + 2}$ có tiệm cận đứng và tiệm cận ngang lần lượt là

A. $x = 2; y = 2$

B. $x = 2; y = - 2$

C. $x = - 2; y = - 2$

D. $x = - 2; y = 2$

Xem đáp án

Đáp án là B.

Dễ nhận thấy đồ thị hàm số có tiệm cận đứng và tiệm cận ngang là: $x = 2; y = - 2.$

Câu 34:

Cho hàm số $y = \frac{x - 1}{x + 1}$ , khẳng định nào sau đây đúng?

A. Nghịch biến trên $ℝ \ \{- 1\}$

B. Đồng biến trên $(- \infty; - 1)$ và $(- 1; + \infty) .$

C. Nghịch biến trên $(- \infty; - 1)$ và $(- 1; + \infty) .$

D. Đồng biến trên $ℝ \ \{- 1\} .$

Xem đáp án

Đáp án là B

$y^{'} = \frac{2}{{(x + 1)}^{2}} > 0; \forall x \neq - 1.$

Câu 35:

Biết đồ thị hàm số $y = x^{4} + b x^{2} + c$ chỉ có một điểm cực trị là điểm có tọa độ $(0; - 1)$ thì b và c thỏa mãn điều kiện nào?

A. $b \geq 0$ và $c = - 1$

B. $b < 0$ và $c = - 1$

C. $b \geq 0$ và $c > 0$

D. $b \geq 0$ và c tùy ý

Xem đáp án

Đáp án là A

$y^{'} = 4 x^{3} + 2 b x, c h o y^{'} = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ x^{2} = \frac{- b}{2} (*) \end{array}$

Đồ thị chỉ có một điểm cực trị nên phương trình (*) có một nghiệm hoặc vô nghiệm, suy ra: $b \geq 0.$

mà điểm $(0; - 1)$ là điểm cực trị của đồ thị nên $c = - 1$

Câu 36:

Phương trình tiếp tuyến với đồ thị hàm số $y = \frac{x + 1}{x - 1}$ song song với đường thẳng $Δ : 2 x + y + 1 = 0$ là

A. $2 x + y = 0$

B. $2 x + y + 7 = 0$

C. $2 x + y - 7 = 0$

D. $- 2 x - y - 1 = 0$

Xem đáp án

Đáp án là C

$y^{'} = \frac{- 2}{{(x - 1)}^{2}}$ . Gọi $M (x_{0}; y_{0}) \in (C)$ là tiếp điểm.

Vì tiếp tuyến song song với đường thẳng $y = - 2 x - 1$ nên:

$\frac{- 2}{{(x_{0} - 1)}^{2}} = - 2 \Leftrightarrow {(x_{0} - 1)}^{2} = 1 \Leftrightarrow [\begin{array}{l} x_{0} = 2 \Rightarrow y_{0} = 3 \\ x_{0} = 0 \Rightarrow y_{0} = - 1 \end{array}$

Phương trình tiếp tuyến cần tìm: $2 x + y - 7 = 0.$

Câu 37:

Tập xác định của hàm số $y = \frac{1 - \cos x}{\sin x - 1}$ là

A. $ℝ \ \{\frac{π}{2} + k 2 π\}$

B. $ℝ \ \{\frac{π}{2} + k π\}$

C. $ℝ \ \{k 2 π\}$

D. $ℝ \ \{k π\}$

Xem đáp án

Đáp án là A

Điều kiện: $\sin x \neq 1 \Leftrightarrow x \neq \frac{π}{2} + k 2 π$

Câu 38:

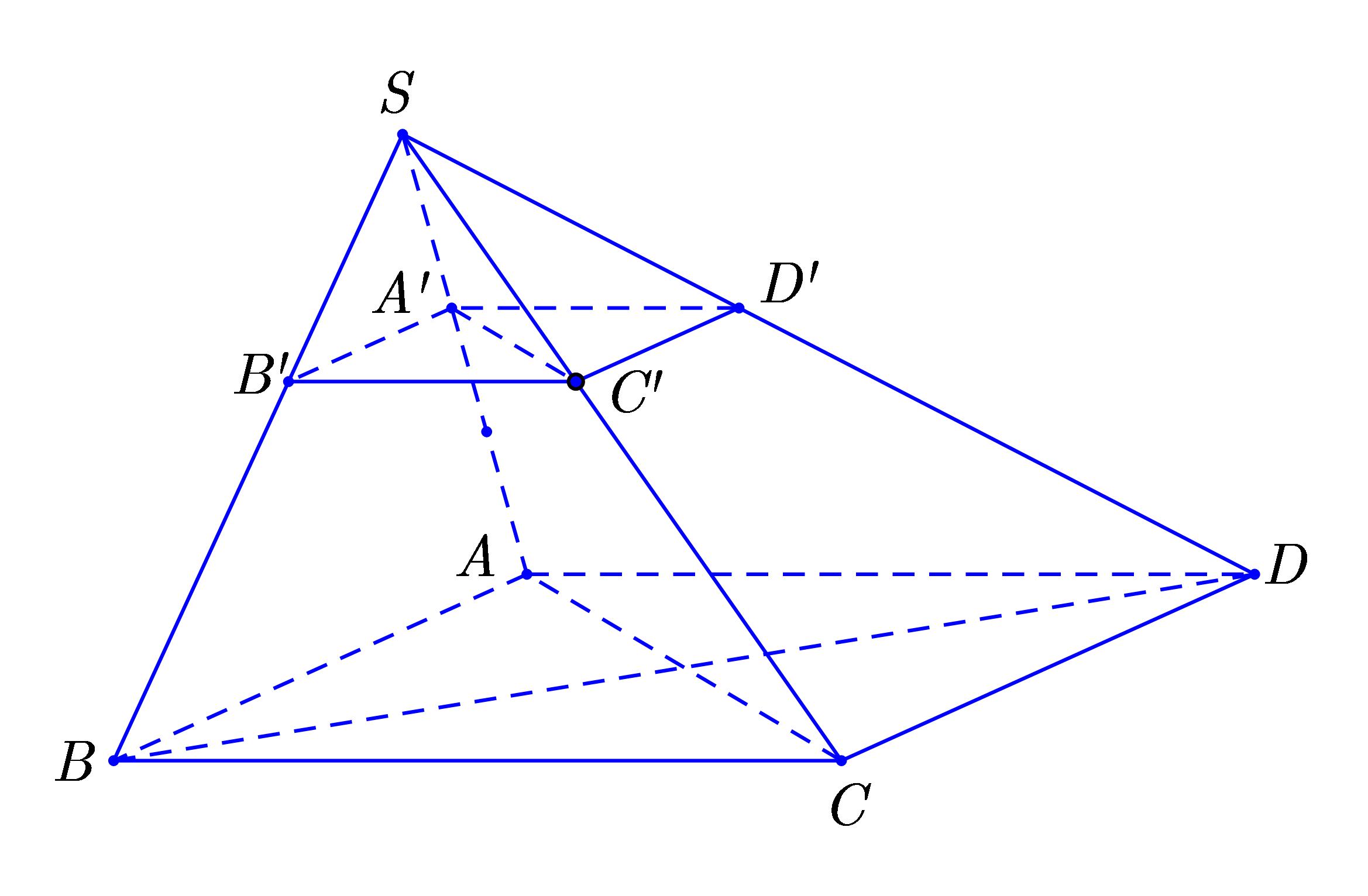
Cho hình chóp tứ giác $S . A B C D$ có thể tích bằng V. Lấy điểm A’ trên cạnh SA sao cho $S A' = \frac{1}{3} S A$ . Một mặt phẳng qua A’ và song song với đáy của hình chóp cắt các cạnh $S B, S C, S D$ lần lượt tại $B', C', D'$ . Khi đó thể tích của khối chóp $S . A' B' C' D'$ tính theo a bằng

A. $\frac{V}{3}$

B. $\frac{V}{9}$

C. $\frac{V}{27}$

D. $\frac{V}{81}$

Xem đáp án

Đáp án là C

$\frac{V_{S . A^{'} B^{'} C^{'}}}{V_{S . A B C}} = \frac{1}{27} \Rightarrow V_{S . A^{'} B^{'} C^{'}} = \frac{1}{27} V_{S . A B C} \Rightarrow V_{S . A B C D} = 2 V_{S . A^{'} B^{'} C^{'}} = \frac{2}{27} . \frac{1}{2} V_{S . A B C D} = \frac{V}{27} .$

Câu 39:

Cho khối chóp $(H)$ có thể tích là $2 a^{3}$ , đáy là hình vuông cạnh bằng $a \sqrt{2}$ . Độ dài chiều cao của khối chóp $(H)$ bằng

A. 4a

B. 3a

C. 2a

D. a

Xem đáp án

Đáp án là B

$h = \frac{3 V_{(H)}}{S_{h v}} = 3 a$

Câu 40:

Người ta gọt một khối lập phương bằng gỗ để lấy khối tám mặt đều nội tiếp nó (tức là khối có các đỉnh là các tâm của các mặt khối lập phương). Biết cạnh của khối lập phương bằng a . Thể tích khối tám mặt đều đó bằng

A. $\frac{a^{3}}{6}$

B. $\frac{a^{3}}{12}$

C. $\frac{a^{3}}{4}$

D. $\frac{a^{3}}{8}$

Xem đáp án

Đáp án là A

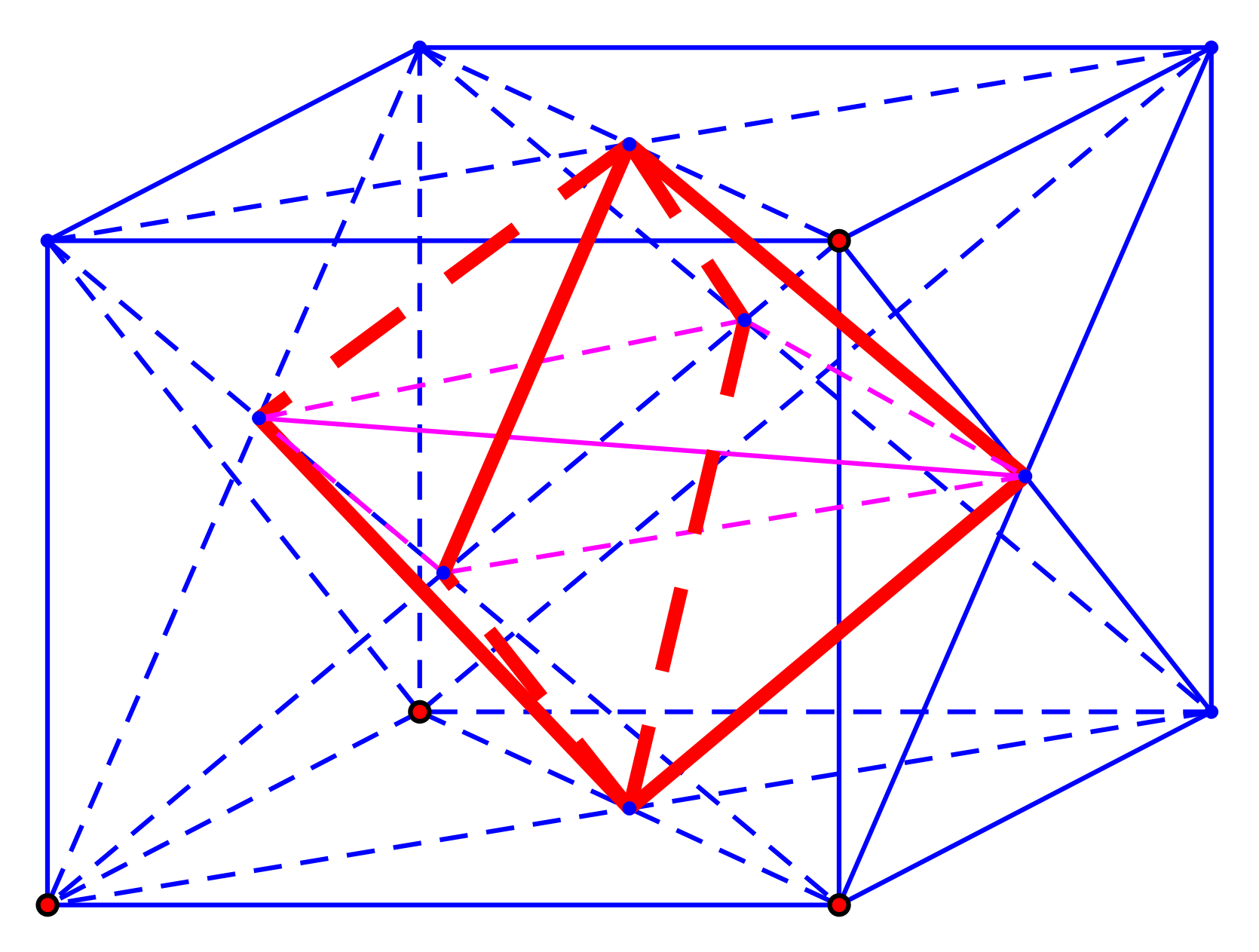
Cạnh của hình bát diện đều bằng:

$\frac{a \sqrt{2}}{2} \Rightarrow S_{d a y} = {(\frac{a \sqrt{2}}{2})}^{2} = \frac{a^{2}}{2}$

Thể tích cần tính: $V = \frac{2}{3} h . S_{d a y} = \frac{2}{3} \frac{a}{2} \frac{a^{2}}{2} = \frac{a^{3}}{6}$

Câu 41:

Mỗi đỉnh của bát diện đều là đỉnh chung của bao nhiêu cạnh?

A. 3

B. 8

C. 5

D. 4

Xem đáp án

Đáp án là D

Câu 42:

Cho hàm số $y = f (x)$ xác định, liên tục trên $ℝ$ và có bảng biến thiên

Khẳng định nào sau đây đúng?

A. Hàm số có giá trị cực tiểu bằng 2

B. Hàm số đặt cực đại tại x=0 và đạt cực tiểu tại x=1

C. Hàm số có đúng một cực trị

D. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng -3

Xem đáp án

Đáp án là B

Từ BBT ta thấy, hàm số đạt cực đại tại x=0 đạt cực tiểu tại x=1.

Câu 43:

Cho hình chóp $S . A B C D$ có đáy $A B C D$ là hình thoi cạnh a, góc $\overset{⏜}{B A C} = 60 °$ , hình chiếu của đỉnh S trên mặt phẳng $(A B C D)$ trùng với trọng tâm tam giác $A B C$ , góc tạo bới hai mặt phẳng $(S A C)$ và $(A B C D)$ là $60 °$ . Khoảng cách từ B đến mặt phẳng $(S C D)$ theo a bằng

A. $\frac{3 a}{2 \sqrt{7}}$

B. $\frac{9 a}{2 \sqrt{7}}$

C. $\frac{a}{2 \sqrt{7}}$

D. $\frac{3 a}{\sqrt{7}}$

Xem đáp án

Đáp án là A.

$d (B; (S C D)) = \frac{3}{2} d (G; (S C D))$

Tính được: $G H = \frac{a \sqrt{3}}{3}; S G = \frac{a}{2}; G K = \frac{a}{\sqrt{7}} .$

Vậy $d (B; (S C D)) = \frac{3}{2} d (G; (S C D)) = \frac{3}{2} . \frac{a}{\sqrt{7}} = \frac{3 a}{2 \sqrt{7}} .$

Câu 44:

Cho khối lăng trụ ABC.A'B'C' có thể tích là V. Thể tích của khối chóp C'ABC bằng

A. $\frac{1}{3} V$

B. $\frac{1}{2} V$

C. $2 V$

D. $\frac{1}{6} V$

Xem đáp án

Đáp án là A.

$\frac{V_{C^{'} . A B C}}{V} = \frac{1}{3} \Rightarrow V_{C^{'}, A B C} = \frac{1}{3} V .$

Câu 45:

Cho hình lăng trụ tam giác đều có các cạnh đều bằng a. Thể tích khối lăng trụ tính theo a bằng

A. $\frac{a^{3}}{3}$

B. $\frac{2 a^{3} \sqrt{2}}{3}$

C. $\frac{a^{3} \sqrt{3}}{4}$

D. $\frac{2 a^{3}}{3}$

Xem đáp án

Đáp án là C

$V = a . \frac{a^{2} \sqrt{3}}{4} = \frac{a^{3} \sqrt{3}}{4} .$

Câu 46:

Cho khối chóp $S . A B C D$ có đáy $A B C D$ là hình thoi cạnh a, $S A = S B = S C = a$ , cạnh SD thay đổi. Thể tích lớn nhất của khối chóp $S . A B C D$ bằng

A. $\frac{a^{3}}{8}$

B. $\frac{a^{3}}{2}$

C. $\frac{3 a^{3}}{8}$

D. $\frac{a^{3}}{4}$

Xem đáp án

Đáp án là D.

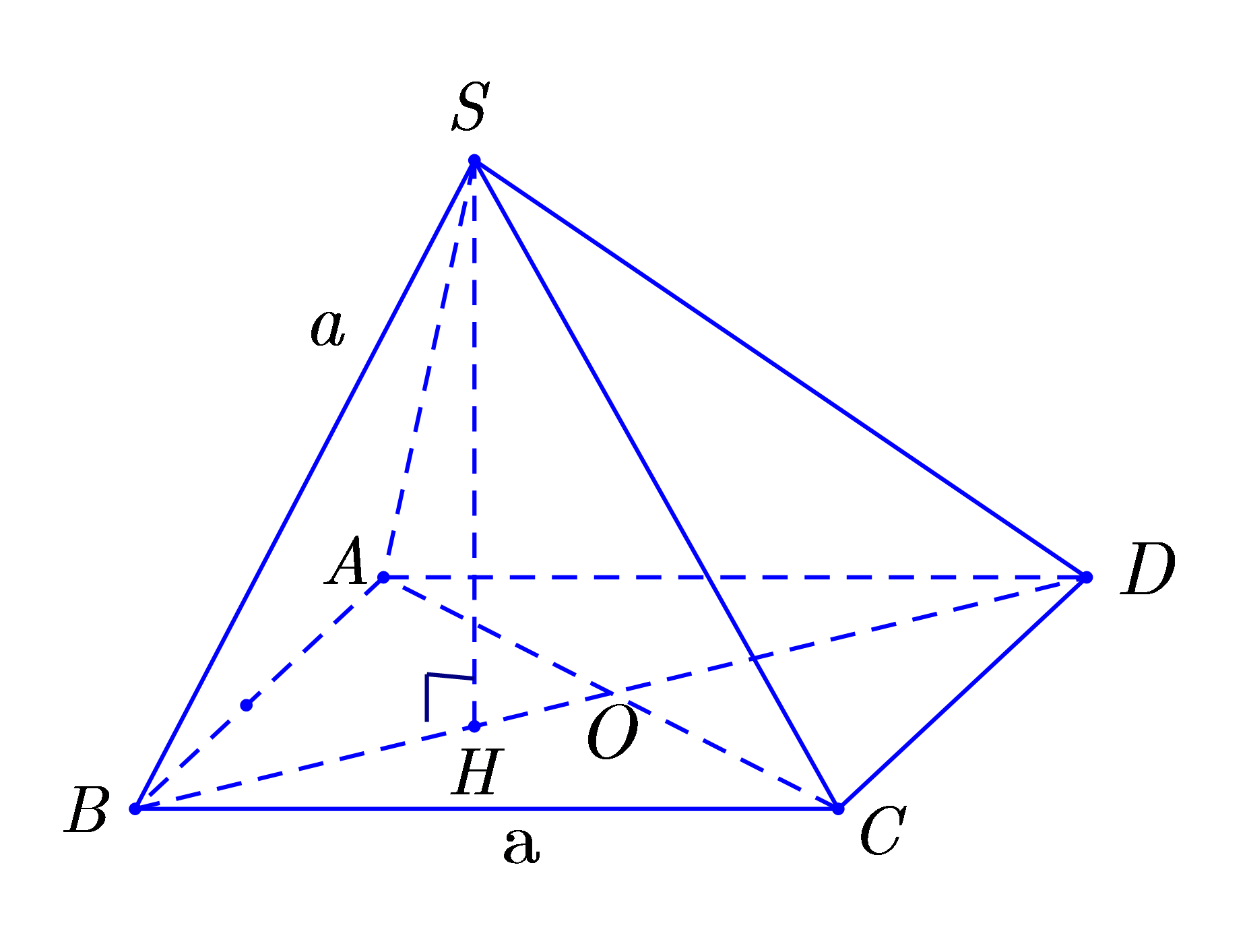
Khi SD thay đổi thi AC thay đổi. Đặt AC = x.

Gọi $O = A C \cap B D$ .

Vì $S A = S B = S C$ nên chân đường cao SH trùng với tâm đường tròn ngoại tiếp tam giác ABC.

$\Rightarrow H \in B O$

Ta có: $O B = \sqrt{a^{2} - {(\frac{x}{2})}^{2}} = \sqrt{\frac{4 a^{2} - x^{2}}{4}} = \frac{\sqrt{4 a^{2} - x^{2}}}{2}$

$S_{A B C} = \frac{1}{2} O B . A C = \frac{1}{2} x . \frac{\sqrt{4 a^{2} - x^{2}}}{2} = \frac{x \sqrt{4 a^{2} - x^{2}}}{4}$

$H B = R = \frac{a . a . x}{4 S_{A B C}} = \frac{a^{2} x}{4. \frac{x \sqrt{4 a^{2} - x^{2}}}{4}} = \frac{a^{2}}{\sqrt{4 a^{2} - x^{2}}}$

$S H = \sqrt{S B^{2} - B H^{2}} = \sqrt{a^{2} - \frac{a^{4}}{4 a^{2} - x^{2}}} = \frac{a \sqrt{3 a^{2} - x^{2}}}{\sqrt{4 a^{2} - x^{2}}}$

$= \frac{1}{3} a (x . \sqrt{3 a^{2} - x^{2}}) \leq \frac{1}{3} a (\frac{x^{2} + 3 a^{2} - x^{2}}{2}) = \frac{a^{3}}{2}$

Câu 47:

Gieo đồng thời hai con súc sắc. Xác suất để số chấm trên mặt xuất hiện của cả hai con súc sắc đều là số chẵn bằng

A. $\frac{1}{4}$

B. $\frac{1}{12}$

C. $\frac{1}{36}$

D. $\frac{1}{6}$

Xem đáp án

Đáp án là A

Số phần tử không gian mẫu $n (Ω) = 36$

Gọi biến cố " Số chấm xuất hiện trên mặt của hai con súc sắc là số chẳn".

Ta có các khả năng xảy ra:

$\{2; 2\}; \{2; 4\}; \{2; 6\}; \{4; 4\}; \{4; 6\}; \{6; 6\}; \{4; 2\}; \{6; 2\}; \{6; 4\} \Rightarrow n (A) = 9$

Xác suất cần tính: $P (A) = \frac{1}{4}$

Câu 48:

Cho hình chóp S.ABCD đáy ABCD là hình thang vuông tại A và D, AD=BA=2a, CD=a, góc giữa hai mặt phẳng (SBC) và (ABCD) bằng $60 °$ . Gọi I là trung điểm của cạnh AD. Biết hai mặt phẳng (SBI) và (SCI) cùng vuông góc với mặt phẳng (ABCD). Thể tích khối chóp S.ABCD tính theo a bằng

A. $\frac{3 a^{3} \sqrt{15}}{5}$

B. $\frac{3 a^{3} \sqrt{15}}{15}$

C. $\frac{a^{3} \sqrt{15}}{5}$

D. $\frac{3 a^{3} \sqrt{5}}{15}$

Xem đáp án

Đáp án là A

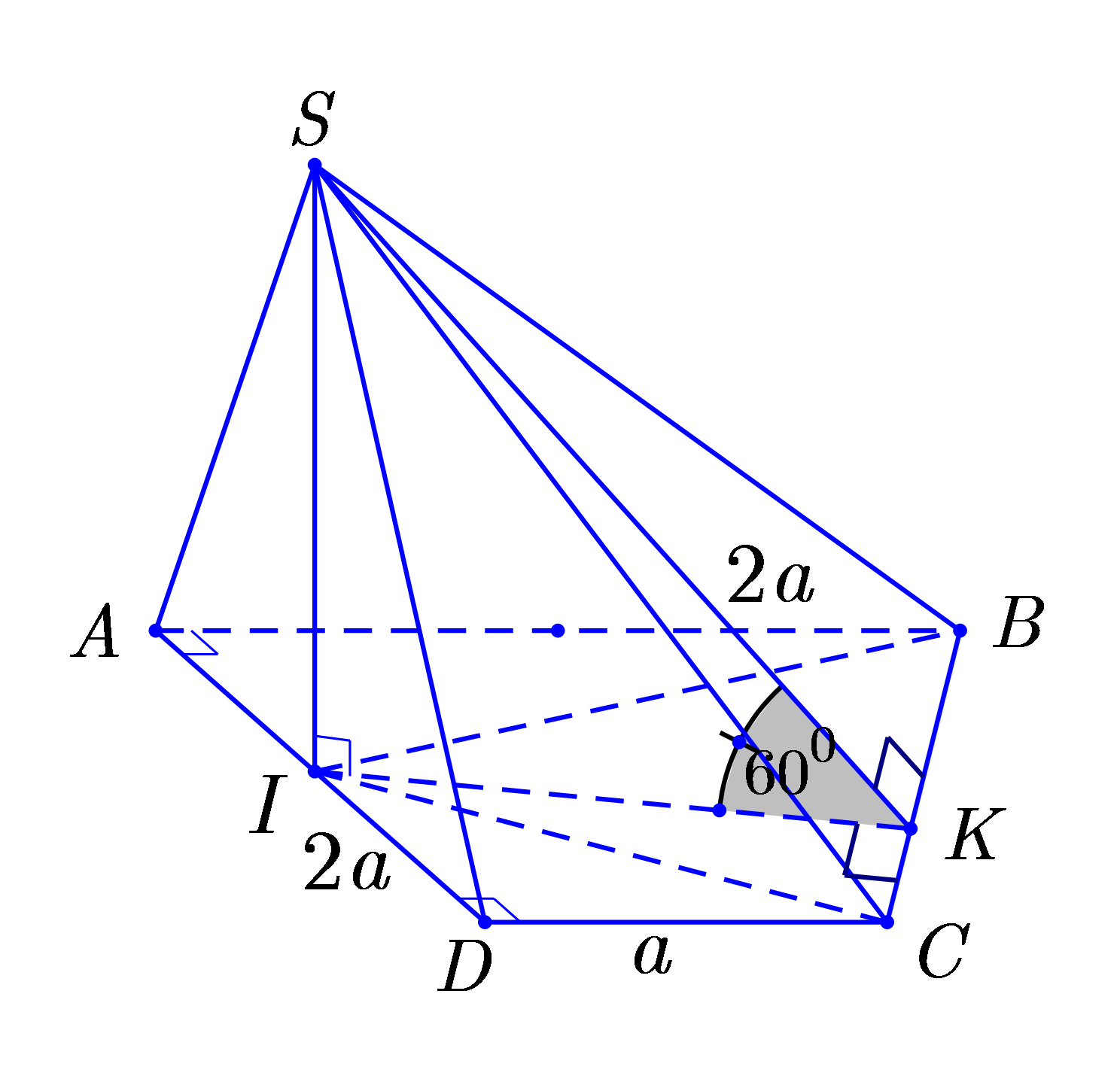
Tính được: $I B = a \sqrt{5}; I C = a \sqrt{2}; B C = a \sqrt{5};$

$S_{A B C D} = 3 a^{2}; I K = \frac{3 a}{\sqrt{5}}; S I = \frac{3 a \sqrt{15}}{5}$

Vậy: $V_{S . A B C D} = \frac{1}{3} S I . S_{A B C D} = \frac{3 a^{3} \sqrt{15}}{5} .$

Câu 49:

Cho hàm số $y = x^{4} - 2 x^{2} + m - 3 (C)$ .Tất cả các giá trị của m để (C) cắt trục Ox tại 4 điểm phân biệt.

A. $- 4 < m < - 3$

B. $3 < m < 4$

C. $- 4 \leq m < 3$

D. $3 < m \leq 4$

Xem đáp án

Đáp án là B

Phương trình hoành độ giao điểm của (C) và trục: $x^{4} - 2 x^{2} + m - 3 = 0$

Đặt $t = x^{2} \geq 0 \Rightarrow t^{2} - 2 t + m - 3 = 0 (*)$

(C) cắt Ox tại 4 điểm phân biệt khi phương trình (*) có hai nghiệm phân biệt dương.

$\{\begin{cases} Δ^{'} > 0 \\ S > 0 \\ P > 0 \end{cases} \Leftrightarrow \{\begin{cases} - m + 4 > 0 \\ m - 3 > 0 \end{cases} \Leftrightarrow 3 < m < 4.$

Câu 50:

Cho hàm số $y = f (x)$ có đạo hàm trên tập K. Gọi $x_{0} \in K$ , khi đó $x = x_{0}$ được gọi là điểm cực đại của hàm số $y = f (x)$ nếu

A. $f' (x)$ đổi dấu khi x đi qua giá trị $x = x_{0}$ .

B. $f' (x) = 0$

C. $f' (x)$ đổi dấu từ âm sang dương khi x đi qua giá trị $x = x_{0}$ .

D. $f' (x)$ đổi dấu từ dương sang âm khi x đi qua giá trị $x = x_{0}$ .

Xem đáp án

Đáp án là D