50 câu hỏi trắc nghiệm thuộc Tổng hợp 20 đề thi thử THPTQG môn Toán cực hay có đáp án (đề 19)

Câu 1:

Hàm số nào sau đây nghịch biến trên từng khoảng xác định?

A. $y = x^{4} - x^{2}$

B. $y = - x^{3} + 3 x^{2}$

C. $y = 2 x - \sin x$

D. $y = \frac{x - 1}{x - 2}$

Xem đáp án

Đáp án D

Xét hàm số $y = \frac{x - 1}{x - 2} .$ Ta có: $y' = - \frac{1}{{(x - 2)}^{2}} < 0 \forall x \in (- \infty; 2) \cup (2; + \infty) \Rightarrow$ hàm số nghịch biến trên từng khoảng xác định.

Câu 2:

Tất cả các giá trị của m để hàm số $y = (m - l) x^{3} - 3 (m - l) x^{2} + 3 (2 m - 5) x + m$ nghịch biến trên R là:

A. $m < 1$

B. $m \leq 1$

C. $m = 1$

D. $- 4 < m < 1$

Xem đáp án

Đáp án B

Ta có: $y' = 3 (m - 1) x^{2} - 6 (m - 1) x + 3 (2 m - 5)$ .

Để hàm số nghịch biến trên R thì: $\begin{array}{l} y' \leq 0 \forall x \in ℝ \end{array}$

$\Leftrightarrow 3 (m - 1) x^{2} - 6 (m - 1) x + 3 (2 m - 5) \leq 0 \forall x \in ℝ$

$\Leftrightarrow (m - 1) x^{2} - 2 (m - 1) x + 2 m - 5 \leq 0 \forall x \in ℝ$

TH1: $m - 1 = 0 \Leftrightarrow m = 1 \Rightarrow - 3 < 0$ (luôn đúng)

TH2: $\{\begin{cases} m - 1 < 0 \\ Δ' = {(m - 1)}^{2} - (2 m - 5) (m - 1) \leq 0 \end{cases} \Leftrightarrow m < 1$

Vậy $m \leq - 1.$

Câu 3:

Số điểm cực trị của hàm số $y = x + \sqrt{2 x^{2} + 1}$ là:

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Đáp án B

Ta có:

$\begin{array}{l} y' = 1 + \frac{4 x}{2 \sqrt{2 x^{2} + 1}} = 1 + \frac{2 x}{\sqrt{2 x^{2} + 1}} = \frac{\sqrt{2 x^{2} + 1} + 2 x}{\sqrt{2 x^{2} + 1}} = 0 \end{array}$

$\Leftrightarrow \sqrt{2 x^{2} + 1} + 2 x = 0 \Leftrightarrow \sqrt{2 x^{2} + 1} = - 2 x$

$\Leftrightarrow \{\begin{cases} x \leq 0 \\ 2 x^{2} + 1 = 4 x^{2} \end{cases} \Leftrightarrow \{\begin{cases} x \leq 0 \\ x = \pm \frac{1}{\sqrt{2}} \end{cases} \Leftrightarrow x = - \frac{1}{\sqrt{2}}$

=> hàm số có 1 điểm cực trị.

Câu 4:

Cho hàm số y=f(x) liên tục trên R, đồ thị của đạo hàm f'(x) như hình vẽ sau:

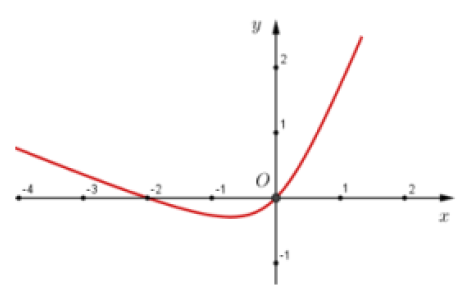
Trong các mệnh đề sau, mệnh đề nào sai?

A. f đạt cực tiểu tại x=0

B. f đạt cực tiểu tại x=-2

C. f đạt cực đại tại x=-2

D. cực tiểu của f nhỏ hơn cực đại.

Xem đáp án

Đáp án B

Quan sát đồ thị hàm số $y = f' (x)$ ta có:

$f' (x) > 0 \Leftrightarrow [\begin{array}{l} x < - 2 \\ x > 0 \end{array}, f' (x) < 0 \Leftrightarrow - 2 < x < 0 \Rightarrow$ B sai; A,C và D đúng.

Câu 5:

Với giá trị nào của tham số m thì phương trình $x + \sqrt{4 - x^{2}} = m$ có nghiệm?

A. $- 2 < m < 2$

B. $- 2 < m < 2 \sqrt{2}$

C. $- 2 \leq m \leq 2 \sqrt{2}$

D. $- 2 \leq m \leq 2$

Xem đáp án

Đáp án C

Ta có: $(x + \sqrt{4 - x^{2}}) \leq (1^{2} + 1^{2}) (x^{2} + 4 - x^{2}) = 8$

$\Rightarrow - 2 \sqrt{2} \leq x + \sqrt{4 - x^{2}} \leq 2 \sqrt{2} \Rightarrow$ để phương trình có nghiệm thì $- 2 \sqrt{2} \leq m \leq 2 \sqrt{2} .$

Câu 6:

Cho hệ $\{\begin{cases} 9 x^{2} - 4 y^{2} = 5 \\ \log_{m} (3 x + 2 y) - \log_{3} (3 x - 2 y) = 1 \end{cases}$ có nghiệm $(x; y)$ thỏa mãn $3 x + 2 y \leq 5.$ Khi đó giá trị lớn nhất của m là

A. -5

B. $\log_{3} 5$

C. 5

D. $\log_{5} 3$

Xem đáp án

Đáp án C

Ta có: $9 x^{2} - 4 y^{2} = 5 \Leftrightarrow (3 x + 2 y) (3 x - 2 y) = 5 \Leftrightarrow 3 x - 2 y = \frac{5}{3 x + 2 y}$

Khi đó: $\log_{m} (3 x + 2 y) = \log_{3} (3 x - 2 y) = 1$

$\Leftrightarrow \log_{m} (3 x + 2 y) - \log_{3} (\frac{5}{3 x + 2 y}) = 1$

$\begin{array}{l} \Leftrightarrow \log_{m} (3 x + 2 y) + \log_{3} (3 x + 2 y) - \log_{3} 5 = 1 \\ \Leftrightarrow \log_{m} 3. \log_{3} (3 x + 2 y) + \log_{3} (3 x + 2 y) = \log_{3} 15 \\ \Leftrightarrow \log_{3} (3 x + 2 y) [1 + \log_{m} 3] = \log_{3} 15 \end{array}$

Vì $3 x + 2 y \leq 5$

nên $\log_{3} (3 x + 2 y) \leq \log_{3} 5 \Rightarrow \frac{\log_{3} 15}{1 + \log_{m} 3} \leq \log_{3} 5$

$\Leftrightarrow \frac{\log_{3} 15}{\log_{3} 5} \leq 1 + \log_{m} 3$

$\Leftrightarrow \log_{m} 3 \geq \log_{5} 15 - 1 = \log_{5} 3 \Leftrightarrow m \leq 5.$

Câu 7:

Đồ thị hàm số nào sau đây có ba đường tiệm cận?

A. $y = \frac{1 - 2 x}{1 + x}$

B. $y = \frac{1}{4 - x^{2}}$

C. $y = \frac{x + 3}{5 x - 1}$

D. $y = \frac{x}{x^{2} - x + 9}$

Xem đáp án

Đáp án B

Xét hàm số $y = \frac{1}{4 - x^{2}} .$ Ta có: $\lim_{x \to \pm 2} y = \infty \Rightarrow x = \pm 2$ là TCĐ. $\lim_{x \to \infty} y = \lim_{x \to \infty} \frac{1}{4 - x^{2}} = 0 \Rightarrow y = 0$ là TCN.

Câu 8:

Đường cong ở hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây.

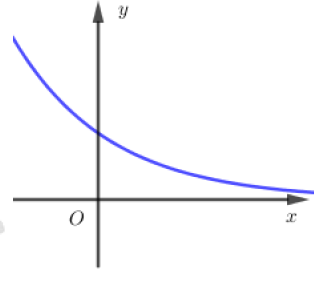
Hỏi hàm số đó là hàm số nào?

A. $y = - x^{2} + 2 x + 1$

B. $y = \log_{0, 5} x$

C. $y = \frac{1}{2^{x}}$

D. $y = 2^{x}$

Xem đáp án

Đáp án C

Câu 9:

Cho a, b, c là ba số thực dương và khác 1. Đồ thị các hàm số $y = \log_{a} x, y = \log_{b} x, y = \log_{c} x$ được cho trong hình vẽ bên.

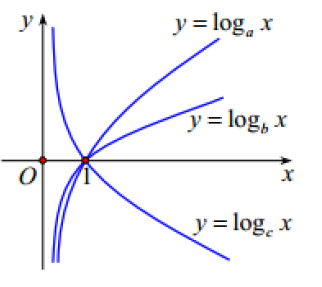
Mệnh đề nào dưới đây là mệnh đề đúng?

A. $a < b < c$

B. $c < a < b$

C. $c < b < a$

D. $b < c < a$

Xem đáp án

Đáp án B

Hàm số $y = \log_{c} x$ nghịch biến $\Rightarrow 0 < c < 1,$ các hàm $y = \log_{a} x, y = \log_{b} x$ đồng biến nên $a; b > 1$ Chọn $x = 100 \Rightarrow \log_{a} 100 > \log_{b} 100 \Rightarrow a < b \Rightarrow c < a < b .$

Câu 10:

Cho phương trình $x^{3} - 3 x^{2} + 1 - m = 0 (1) .$ Điều kiện của tham số m để phương trình (1) có ba nghiệm phân biệt thỏa mãn $x_{1} < 1 < x_{2} < x_{3}$ là

A. $m = - 1$

B. $- 1 < m < 3$

C. $- 3 < m < - 1$

D. $- 3 \leq m \leq - 1$

Xem đáp án

Đáp án C

Vẽ đồ thị hàm số $y = x^{3} - 3 x^{2} + 1$

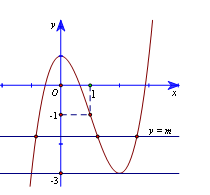
Để phương trình (1) có ba nghiệm phân biệt thỏa mãn $x_{1} < 1 < x_{2} < x_{3}$ thì đường thẳng y=m cắt đồ thị hàm số $y = x^{3} - 3 x^{2} + 1$ tại ba điểm phân biệt thỏa mãn $x_{1} < 1 < x_{2} < x_{3} \Leftrightarrow - 3 < m < - 1.$

Câu 11:

Cho a, b là các số thực dương. Rút gọn biểu thức $P = \frac{{(\sqrt[4]{a^{3} b^{2}})}^{4}}{\sqrt[3]{\sqrt{a^{12} b^{6}}}}$ được kết quả là

A. $a b^{2}$

B. $a^{2} b$

C. ab

D. $a^{2} b^{2}$

Xem đáp án

Đáp án C

Ta có: $P = \frac{{(\sqrt[4]{a^{3} b^{2}})}^{4}}{\sqrt[3]{a^{12} b^{6}}} = \frac{a^{3} b^{2}}{\sqrt[3]{a^{6} b^{3}}} = \frac{a^{3} b^{2}}{a^{2} b} = a b .$

Câu 12:

Cho $f (x) = \frac{2018^{x}}{2018^{x} + \sqrt{2018}} .$ Giá trị của biểu thức:

$S = f (\frac{1}{2017}) + f (\frac{2}{2017}) + ... + f (\frac{2016}{2017})$ là

A. 2017

B. 1008

C. $\sqrt{2016}$

D. 1006

Xem đáp án

Đáp án B

Ta có: $f (x) + f (1 - x) = 1$ .

Suy ra $S = f (\frac{1}{2017}) + f (\frac{2}{2017}) + ... + f (\frac{2016}{2017})$

$= \frac{2016}{2} [f (x) + f (1 - x)] = 1008.$

Câu 13:

Cho n là số nguyên dương và $a > 0, a \neq 1.$

Tìm n sao cho: $\log_{a} 2019 + \log_{\sqrt{a}} 2019 + ... + \log_{\sqrt[n]{a}} 2019 = 2033136 \log_{a} 2019.$

A. $n = 2017$

B. $n = 2016$

C. $n = 2018$

D. $n = 2019$

Xem đáp án

Đáp án B

Ta có: $\begin{array}{l} \log_{a} 2019 + \log_{\sqrt{a}} 2019 + ... + \log_{\sqrt[n]{a}} 2019 \end{array}$

$\begin{array}{l} = \log_{a} 2019 + 2 \log_{2019} + ... + n \log_{a} 2019 \end{array}$

$\begin{array}{l} = \log_{a} 2019 (1 + 2 + ... + n) = \frac{n}{2} (n + 1) \log_{a} 2019 \end{array}$

$\begin{array}{l} = 2033136 \log_{a} 2019 \Rightarrow \frac{n}{2} (n + 1) = 2033136 \end{array}$

$\Leftrightarrow n^{2} + n - 4066272 = 0 \Leftrightarrow [\begin{array}{l} n = 2016 \\ n = - 2017 \end{array} \Rightarrow n = 2016.$

Câu 14:

Giải phương trình ${(2, 5)}^{5 x - 7} = {(\frac{2}{5})}^{x + 1} .$

A. $x \geq 1$

B. $x = 1$

C. $x < 1$

D. $x = 2$

Xem đáp án

Đáp án B

$P T \Leftrightarrow {(\frac{5}{2})}^{5 x - 7} = {(\frac{5}{2})}^{- x - 1} \Leftrightarrow 5 x - 7 = - x - 1 \Leftrightarrow x = 1.$

Câu 15:

Tập nghiệm của bất phương trình $9^{x} - 2 (x + 5) 3^{x} + 9 (2 x + 1) \geq 0$ là

A. $[0; 1] \cup [2; + \infty)$

B. $(- \infty; 1] \cup [2; + \infty)$

C. $[1; 2]$

D. $(- \infty; 0] \cup [2; + \infty)$

Xem đáp án

Đáp án A

$B P T \Leftrightarrow (3^{x} - 2 x - 1) (3^{x} - 9) \geq 0 \Leftrightarrow [\begin{array}{l} \{\begin{cases} 3^{x} \geq 2 x + 1 \\ 3^{x} \geq 9 \end{cases} \\ \{\begin{cases} 3^{x} \leq 2 x + 1 \\ 3^{x} \leq 9 \end{cases} \end{array} \Leftrightarrow [\begin{array}{l} \{\begin{cases} 3^{x} \geq 2 x + 1 \\ x \geq 2 \end{cases} \\ \{\begin{cases} 3^{x} \leq 2 x + 1 \\ x \leq 2 \end{cases} \end{array} (1) .$

$P T 3^{x} = 2 x + 1$ có hai nghiệm $x = 0, x = 1.$

Suy ra $(1) \Leftrightarrow [\begin{array}{l} \{[\begin{array}{l} x \geq 1 \\ x \leq 0 \end{array} \\ \{\begin{cases} 0 \leq x \leq 1 \\ x \leq 2 \end{cases} \end{array} \Leftrightarrow [\begin{array}{l} x \geq 2 \\ 0 \leq x \leq 1 \end{array} \Rightarrow S = [0; 1] \cup [2; + \infty) .$

Câu 16:

Phương trình $\log_{3} (3 x - 2) = 3$ có nghiệm là

A. $x = \frac{29}{3}$

B. $x = \frac{11}{3}$

C. $x = \frac{25}{3}$

D. $x = 87$

Xem đáp án

Đáp án A

$P T \Leftrightarrow \{\begin{cases} 3 x - 2 > 0 \\ 3 x - 2 = 27 \end{cases} \Rightarrow 3 x - 2 = 27 \Leftrightarrow x = \frac{29}{3} .$

Câu 17:

Tập nghiệm của bất phương trình $\log_{2} (x^{2} - 3 x + 1) \leq 0$ là

A. $S = [0; \frac{3 - \sqrt{5}}{2}) \cup (\frac{3 + \sqrt{5}}{2}; 3]$

B. $S = (0; \frac{3 - \sqrt{5}}{2}) \cup (\frac{3 + \sqrt{5}}{2}; 3)$

C. $[\frac{3 - \sqrt{5}}{2}; \frac{3 + \sqrt{5}}{2}]$

D. $S = \emptyset$

Xem đáp án

Đáp án A

$\begin{array}{l} B P T \Leftrightarrow \{\begin{cases} x^{2} - 3 x + 1 > 0 \\ x^{2} - 3 x + 1 \leq 1 \end{cases} \Leftrightarrow \{\begin{cases} [\begin{array}{l} x > \frac{3 + \sqrt{5}}{2} \\ x < \frac{3 - \sqrt{5}}{2} \end{array} \\ 0 \leq x \leq 3 \end{cases} \Leftrightarrow [\begin{array}{l} 0 \leq x < \frac{3 - \sqrt{5}}{2} \\ \frac{3 + \sqrt{5}}{2} < x \leq 3 \end{array} \end{array}$

$\Rightarrow S = [0; \frac{3 - \sqrt{5}}{2}) \cup (\frac{3 + \sqrt{5}}{2}; 3] .$

Câu 18:

Phương trình $25^{x} - {2.10}^{x} + m^{2} 4^{x} = 0$ có hai nghiệm trái dấu khi

A. $m \in (- 1; 0) \cup (0; 1)$

B. $m \leq 1$

C. $[\begin{array}{l} m < - 1 \\ m > 1 \end{array}$

D. $m \geq - 1$

Xem đáp án

Đáp án A

$P T \Leftrightarrow {(\frac{5}{2})}^{2 x} - 2 {(\frac{5}{2})}^{x} + m^{2} = 0 \overset{t - {(\frac{5}{2})}^{x}}{\to} t^{2} - 2 t + m^{2} = 0 (1) .$

PT ban đầu có 2 nghiệm trái dấu $\Leftrightarrow (1)$ có hai nghiệm thỏa mãn $0 < t_{1} < 1 < t_{2} .$

Suy ra $\{\begin{cases} Δ' (1) > 0 \\ t_{1} + t_{2} > 0 \\ t_{1} t_{2} > 0 \\ (t_{1} - 1) (t_{2} - 1) < 0 \end{cases} \Leftrightarrow \{\begin{cases} 1 - m^{2} > 0 \\ 2 > 0 \\ m^{2} > 0 \\ t_{1} t_{2} - (t_{1} + t_{2}) + 1 < 0 \end{cases}$

$\Leftrightarrow \{\begin{cases} - 1 < m < 1 \\ m \neq 0 \\ m^{2} - 2 + 1 < 0 \end{cases} \Leftrightarrow \{\begin{cases} - 1 < m < 1 \\ m \neq 0 \end{cases} .$

Câu 19:

Tìm số nghiệm của phương trình $2^{x} + 3^{x} + 4^{x} + ... + 2017^{x} + 2018^{x} = 2017 - x .$

A. 1

B. 2016

C. 2017

D. 0

Xem đáp án

Đáp án A

Xét hàm số $f (x) = 2^{x} + 3^{x} + 4^{x} + ... + 2018^{x}$

$f' (x) = 2^{x} \ln 2 + 3^{x} \ln 3 + 4^{x} \ln 4 + ... + 2018^{x} \ln 2018$

Suy ra $f' (x) > 0, \forall x \in ℝ \Rightarrow f (x)$ đồng biến trên

Xét hàm số $g (x) = 2017 - x, g' (x) = - 1 < 0, \forall x \in ℝ$

$\Rightarrow g (x)$ nghịch biến trên

Suy ra $P T \Leftrightarrow f (x) = g (x) \Rightarrow P T$ có nghiệm thì là nghiệm duy nhất.

Dễ thấy x=0 là nghiệm PT đã cho. Suy ra PT đã cho có 1 nghiệm duy nhất. x=0.

Câu 20:

Phương trình $\log_{4} {(x + 1)}^{2} + 2 = \log_{\sqrt{2}} \sqrt{4 - x} + \log_{8} {(4 + x)}^{3}$ có bao nhiêu nghiệm?

A. Vô nghiệm

B. 1 nghiệm

C. 2 nghiệm

D. 3 nghiệm

Xem đáp án

Đáp án C

Điều kiện $\{\begin{cases} {(x + 1)}^{2} > 0 \\ 4 - x > 0 \\ {(4 + x)}^{3} > 0 \end{cases} \Leftrightarrow \{\begin{cases} x \neq - 1 \\ x < 4 \\ x > - 4 \end{cases} \Leftrightarrow \{\begin{cases} - 4 < x < 4 \\ x \neq - 1 \end{cases}$

$P T \Leftrightarrow \log_{2} \sqrt{{(x + 1)}^{2}} + 2 = \log_{2} (4 - x) + \log_{2} (4 + x) \Leftrightarrow \log_{2} [4 \sqrt{{(x + 1)}^{2}}] = \log_{2} (4 - x) (4 + x)$

$\begin{array}{l} \Leftrightarrow 4 \sqrt{{(x + 1)}^{2}} = 16 - x^{2} \Leftrightarrow [\begin{array}{l} \{\begin{cases} x + 1 \geq 0 \\ 4 (x + 1) = 16 - x^{2} \end{cases} \\ \{\begin{cases} x + 1 < 0 \\ - 4 (x + 1) = 16 - x^{2} \end{cases} \end{array} \\ \Leftrightarrow [\begin{array}{l} \{\begin{cases} x \geq - 1 \\ x^{2} + 4 x - 12 = 0 \end{cases} \\ \{\begin{cases} x < - 1 \\ x^{2} - 4 x - 20 = 0 \end{cases} \end{array} \Leftrightarrow [\begin{array}{l} \{\begin{cases} x \geq - 1 \\ [\begin{array}{l} x = 2 \\ x = - 6 \end{array} \end{cases} \\ \{\begin{cases} x < - 1 \\ [\begin{array}{l} x = 2 + 2 \sqrt{6} \\ x = 2 - 2 \sqrt{6} \end{array} \end{cases} \end{array} \\ \Leftrightarrow [\begin{array}{l} x = 2 \\ x = 2 - 2 \sqrt{6} \end{array} \end{array}$

Câu 21:

Một sinh viên ra tiường đi làm vào ngày 1/1/2018 với mức lương khởi điểm là a đồng/ 1 tháng và cứ sau 2 năm lại được tăng thêm 10% và chi tiêu hàng tháng của anh ta là 40% lương. Anh ta dự định mua một căn nhà có giá trị tại thời điểm 1/1/2018 là 1 tỷ đồng và cũng sau 2 năm thì giá trị căn nhà tăng thêm 5%. Với a bằng bao nhiêu thì sau đúng 10 năm anh ta mua được ngôi nhà đó, biết rằng mức lương và mức tăng giá trị ngôi nhà là không đổi? ( kết quả quy tròn đến hàng nghìn đồng)

A. 21.776.000 đồng

B. 55.033.000 đồng

C. 14.517.000 đồng

D. 11.47.000 đồng

Xem đáp án

Đáp án C

Mức giá ngôi nhà sau 10 năm bằng $10^{9} (1 + 5 %)$ đồng.

Số tiền: $24.0, 6 a + 24.0, 6 a (1 + 10 %) + 24.0, 6 a {(1 + 10 %)}^{2}$

$+ 24.0, 6 a {(1 + 10 %)}^{3} + 24.0, 6 a {(1 + 10 %)}^{4}$ đồng.

$\begin{array}{l} \Rightarrow 24.0, 6 a + 24.0, 6 a (1 + 10 %) + 24.0, 6 a {(1 + 10 %)}^{2} \\ + 24.0, 6 a {(1 + 10 %)}^{3} + 24.0, 6 a {(1 + 10 %)}^{4} \\ = 10^{9} {(1 + 5 %)}^{5} \end{array}$

$\Leftrightarrow 24.0, 6 a \frac{1 - {(1 + 10 %)}^{5}}{1 - (1 + 10 %)} = 10^{9} {(1 + 5 %)}^{5}$

$\Rightarrow a \approx 14.517.000$ đồng

Câu 22:

Một người đàn ông muốn chèo thuyền ở vị trí A tới điểm B về phía hạ lưu bờ đối diện, càng nhanh càng tốt, trên một bờ sông thẳng rộng 3km (như hình vẽ).

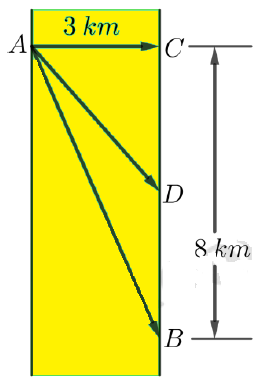
Anh có thể chèo thuyền của mình trực tiếp qua sông để đến C và sau đó chạy đến B, hay có thể chèo trực tiếp đến B, hoặc anh ta có thể chèo thuyền đến một điểm D giữa C và B và sau đó chạy đến B. Biết anh ấy có thể chèo thuyền 6km/h chạy 8km/h và quãng đường BC=8km. Biết tốc độ của dòng nước là không đáng kể so với tốc độ chèo thuyền của người đàn ông. Tìm khoảng thời gian ngắn nhất (đơn vị: giờ) để người đàn ông đến

A. $\frac{3}{2}$

B. $\frac{9}{\sqrt{7}}$

C. $\frac{\sqrt{73}}{6}$

D. $1 + \frac{\sqrt{7}}{8}$

Xem đáp án

Đáp án D

Thời gian đi từ A đến B là $t_{A B} = \frac{\sqrt{3^{2} + 8^{2}}}{6} = \frac{\sqrt{73}}{6} (h)$ .

Thời gian đi từ A đến C rồi đến B là $t_{A C B} = \frac{3}{6} + \frac{8}{8} = \frac{3}{2} (h)$

Gọi $C D = x (k m) \Rightarrow t_{A D B} = \frac{\sqrt{x^{2} + 9}}{6} + \frac{8 - x}{8} (h)$ .

Xét hàm số $f (x) = \frac{\sqrt{x^{2} + 9}}{6} + \frac{8 - x}{8} (0 \leq x \leq 8)$

$f' (x) = \frac{x}{6 \sqrt{x^{2} + 9}} - \frac{1}{8} \Rightarrow f' (x) = 0 \Leftrightarrow x = \frac{9}{\sqrt{7}}$ .

Suy ra $f (0) = \frac{3}{2} = t_{A C B}, f (8) = \frac{73}{6} = t_{A B}, f (\frac{9}{\sqrt{7}}) = 1 + \frac{\sqrt{7}}{8} .$

Suy ra thời gian ngắn nhất bằng $1 + \frac{\sqrt{7}}{8} (h) .$

Câu 23:

Đường cong trong hình vẽ bên dưới là đồ thị của một trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây.

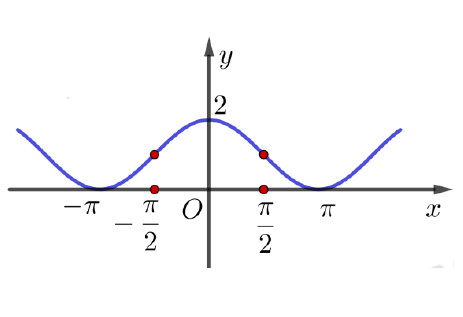
Hỏi hàm số đó là hàm số nào?

A. $y = \cos x + 1$

B. $y = 2 - s inx$

C. $y = 2 \cos x$

D. $y = \cos^{2} x + 1$

Xem đáp án

Đáp án A

Câu 24:

Tập xác định của hàm số $y = - t anx$ là

A. $D = ℝ \ \{\frac{π}{2} + k π; k \in ℤ\}$

B. $D = ℝ \ \{k π; k \in ℤ\}$

C. $D = ℝ \ \{k 2 π; k \in ℤ\}$

D. $D = ℝ \ \{\frac{π}{2} + k 2 π; k \in ℤ\}$

Xem đáp án

Đáp án A

Hàm số xác định $c osx \neq 0$

$\Leftrightarrow x \neq \frac{π}{2} + k π, k \in ℤ \Rightarrow D = ℝ \ \{\frac{π}{2} + k π, k \in ℤ\} .$

Câu 25:

Nghiệm của phương trình $\tan x = - \frac{\sqrt{3}}{3}$ được biểu diễn trên đường tròn lượng giác ở hình bên là những điểm nào?

A. Điểm F, điểm D.

B. Điểm C, điểm F.

C. Điểm C, điểm D, điểm E, điểm F.

D. Điểm E, điểm F.

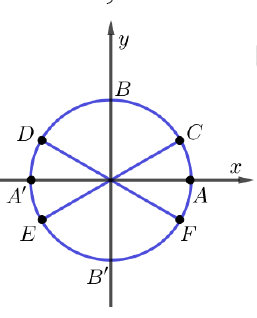
Xem đáp án

Đáp án A

$P T \Leftrightarrow x = - \frac{π}{6} + k π$

Câu 26:

Số giá trị nguyên của tham số m thuộc đoạn $[- 2018; 2018]$ để phương trình $(m + 1) \sin^{2} x - \sin 2 x + c os 2 x = 0$ có nghiệm là:

A. 4037

B. 4036

C. 2019

D. 2020

Xem đáp án

Đáp án D

$P T \Leftrightarrow (m + 1) \frac{1 - c os 2 x}{2} - \sin 2 x + \cos 2 x = 0 \Leftrightarrow \sin 2 x + \frac{m - 1}{2} c os 2 x = \frac{m + 1}{2} .$

PT có nghiệm $\Leftrightarrow 1^{2} + {(\frac{m - 1}{2})}^{2} \geq {(\frac{m + 1}{2})}^{2} \Leftrightarrow m \leq 1.$

Vì $m \in [- 2018; 2018] \Rightarrow$ có 2020 giá trị nguyên của m.

Câu 27:

Nghiệm của phương trình $\sin x \cos x c os 2 x = 0$ là

A. $k π (k \in ℤ)$

B. $k \frac{π}{2} (k \in ℤ)$

C. $k \frac{π}{4} (k \in ℤ)$

D. $k \frac{π}{8} (k \in ℤ)$

Xem đáp án

Đáp án C

$P T \Leftrightarrow \frac{1}{2} \sin 2 x c os 2 x = 0 \Leftrightarrow \frac{1}{4} \sin 4 x = 0 \Leftrightarrow 4 x = k π$

$\Leftrightarrow x = k \frac{π}{4} (\in ℤ)$

Câu 28:

Trong trận đấu bóng đá giữa 2 đội Real madrid và Barcelona, trọng tài cho đội Barcelona được hưởng một quả Penalty. Cầu thủ sút phạt sút ngẫu nhiên vào 1 trong bốn vị trí 1, 2, 3, 4 và thủ môn bay người cản phá ngẫu nhiên đến 1 trong 4 vị trí 1, 2, 3, 4 với xác suất như nhau (thủ môn và cầu thủ sút phạt đều không đoán được ý định của đối phương). Biết nếu cầu thủ sút và thủ môn bay cùng vào vị trí 1 (hoặc 2) thì thủ môn cản phá được cú sút đó, nếu cùng vào vị trí 3 (hoặc 4) thì xác suất cản phá thành công là 50%. Tính xác suất của biến cố “cú sút đó không vào lưới”?

A. $\frac{5}{16}$

B. $\frac{3}{16}$

C. $\frac{1}{8}$

D. $\frac{1}{4}$

Xem đáp án

Đáp án B

Gọi A là biến cố “Cú sút đó không vào lưới”. Nếu cầu thủ sút vào vị trí 1 hoặc 2, xác suất để bóng không vào bằng $2 (\frac{1}{4} . \frac{1}{4}) = \frac{1}{8} .$ Nếu cầu thủ sút cào vị trí 3 hoặc 4, xác suất để bóng không vào bằng $2 (\frac{1}{4} . \frac{1}{4} . \frac{1}{2}) = \frac{1}{16} .$ Suy ra xác suất để bóng không vào bằng $P (A) = \frac{1}{8} + \frac{1}{16} = \frac{3}{16} .$

Câu 29:

Bình A chứa 3 quả cầu xanh, 4 quả cầu đỏ và 5 quả cầu trắng. Bình B chứa 4 quả cầu xanh, 3 quả cầu đỏ và 6 quả cầu trắng. Bình C chứa 5 quả cầu xanh, 5 quả cầu đỏ và 2 quả cầu trắng. Từ mỗi bình lấy một quả cầu. Có bao nhiêu cách lấy để cuối cùng được 3 quả có màu giống nhau.

A. 180

B. 150

C. 120

D. 60

Xem đáp án

Đáp án A

Số cách bằng $3.4.5 + 4.3.5 + 5.6.2 = 180$ cách.

Câu 30:

Tìm số hạng chứa $x^{3} y^{3}$ trong khai triển biểu thức ${(x + 2 y)}^{6}$ thành đa thức.

A. $160 x^{3} y^{3}$

B. $120 x^{3} y^{3}$

C. $20 x^{3} y^{3}$

D. $8 x^{3} y^{3}$

Xem đáp án

Đáp án A

Ta có: ${(x + 2 y)}^{6} = \sum_{k = 0}^{6} C_{6}^{k} x^{6 - k} {(2 y)}^{k} = \sum_{k = 0}^{6} C_{6}^{k} 2^{k} x^{6 - k} y^{k}$ .

Số hạng chứa $x^{3} y^{3} \Rightarrow \{\begin{cases} 6 - k = 3 \\ k = 3 \end{cases} \Rightarrow k = 3 \Rightarrow a_{3} = C_{6}^{3} 2^{3} x^{3} y^{3} = 160 x^{3} y^{3} .$

Câu 31:

Biết rằng hệ số của $x^{n - 2}$ trong khai triển $(x - {\frac{1}{4}}^{n})$ bằng 31. Tìm n .

A. $n = 32$

B. $n = 30$

C. $n = 31$

D. $n = 33$

Xem đáp án

Đáp án A

Hệ số của $x^{n - 2}$ trong khai triển ${(x - \frac{1}{4})}^{n}$ là: $C_{n}^{2} . {(- \frac{1}{4})}^{2} . x^{n - 2}$

Ta có: $C_{n}^{2} . {(- \frac{1}{4})}^{2} = 31$

$\Leftrightarrow \frac{n!}{(n - 2)! 2!} = 496 \Leftrightarrow n (n - 1) = 992 \Leftrightarrow n = 32.$

Câu 32:

Một đội gồm 5 nam và 8 nữ. Lập một nhóm gồm 4 người hát tốp ca, tính xác suất để trong 4 người được chọn có ít nhất 3 nữ ?

A. $\frac{70}{143}$

B. $\frac{73}{143}$

C. $\frac{56}{143}$

D. $\frac{87}{143}$

Xem đáp án

Đáp án A

Xác suất cần tìm là: $P = \frac{C_{8}^{3} . C_{5}^{1} + C_{8}^{4}}{C_{13}^{4}} = \frac{70}{143} .$

Câu 33:

Cho hai đường thẳng song song $d_{1}; d_{2} .$ Trên $d_{1}$ có 6 điểm phân biệt được tô màu đỏ. Trên $d_{2}$ có 4 điểm phân biêt được tô màu xanh. Xét tất cả các tam giác được tạo thành khi nối các điểm đó với nhau. Chọn ngẫu nhiên một tam giác, khi đó xác suất để thu được tam giác có hai đỉnh màu đỏ là:

A. $\frac{5}{32}$

B. $\frac{5}{8}$

C. $\frac{5}{9}$

D. $\frac{5}{7}$

Xem đáp án

Đáp án B

Số tam giác được tạo bởi 2 đỉnh trên $d_{1}$ và 1 đỉnh trên $d_{2}$ là: $C_{6}^{2} . C_{4}^{1} = 60$ . Số tam giác được tạo bởi 1 đỉnh trên $d_{1}$ và 2 đỉnh trên $d_{2}$ là: $C_{6}^{1} . C_{4}^{2} = 36$ .

Do đó số tam giác được tạo thành là: $C_{6}^{2} . C_{4}^{1} + C_{6}^{1} . C_{4}^{2} = 96$ . Xác suất cần tìm là: $\frac{60}{96} = \frac{5}{8} .$

Câu 34:

Cho hàm số $y = \frac{5 x^{3}}{3} - x^{2} + 4$ có đồ thị (C). Tiếp tuyến của (C) tại điểm có hoành độ $x_{0} = 3$ có hệ số góc là:

A. 39

B. 40

C. 51

D. 3

Xem đáp án

Đáp án A

Ta có: $y' = 5 x^{2} - 2 x; k = y' (3) = 5.9 - 2.3 = 39.$

Câu 35:

Tính đạo hàm cấp 2018 của hàm số $y = e^{2 x}$

A. $y^{(2018)} = 2^{2017} e^{2 x}$

B. $y^{(2018)} = 2^{2018} e^{2 x}$

C. $y^{(2018)} = e^{2 x}$

D. $y^{(2018)} = 2^{2018} . x e^{2 x}$

Xem đáp án

Đáp án B

Ta có: $y' = 2 e^{2 x}; y^{(2)} = 2^{2} . e^{2 x} \Rightarrow y^{(2018)} = 2^{2018} e^{2 x} .$

Câu 36:

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật $A B = a; A D = \frac{a \sqrt{3}}{2} .$ Mặt bên SAB là tam giác cân đỉnh S và nằm trong mặt phẳng vuông góc với mặt phẳng. Biết $\overset{⏜}{A S B} = 120^{\circ}$ . Góc giữa hai mặt phẳng (SAD) và (SBC) bằng:

A. $60^{\circ}$

B. $30^{\circ}$

C. $45^{\circ}$

D. $90^{\circ}$

Xem đáp án

Đáp án A

Gọi H là trung điểm của AB .

Lại có: $(S A B) ⊥ (A B C D) \Rightarrow S H ⊥ (A B C D) .$

Do $A D / / B C$ nên giao tuyến d của (SAD) và (SBC) đi qua S và song song với AD.

Do $\{\begin{cases} A D ⊥ A B \\ A D ⊥ S H \end{cases} \Rightarrow A D ⊥ (S A B) \Rightarrow d ⊥ (S A B)$ .Suy ra góc giữa hai mặt phẳng (SAD) và (SBC) bằng $180^{\circ} - \overset{⏜}{AS B} = 60^{\circ} .$

Câu 37:

Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC) và đáy ABC là tam giác vuông tại B, AB=a, SA=a. Gọi H là hình chiếu của A trên SB . Khoảng cách giữa AH và BC bằng:

A. $\frac{a \sqrt{2}}{2}$

B. a

C. $\frac{a}{2}$

D. $\frac{a \sqrt{3}}{2}$

Xem đáp án

Đáp án A

Do $\{\begin{cases} B C ⊥ S A \\ B C ⊥ A B \end{cases} \Rightarrow B C ⊥ (S A B)$ . Khi đó $H B ⊥ B C$ lại có: $H B ⊥ A H \Rightarrow d (A H; B C) = H B$

Tam giác SAB vuông cân tại A nên $\overset{⏜}{A B H} = 45^{\circ}$ .

Do vậy $H B = a \cos \overset{⏜}{A B H} = \frac{a \sqrt{2}}{2} .$

Câu 38:

Hình đa diện sau có bao nhiêu mặt?

A. 11

B. 20

C. 3

D. 6

Xem đáp án

Đáp án A

Câu 39:

Cho hình lăng trụ ABC.A'B'C'. Cắt hình lăng trụ bởi một mặt phẳng ta được một thiết diện. Số cạnh lớn nhất của thiết diện thu được là?

A. 5

B. 4

C. 3

D. 6

Xem đáp án

Đáp án A

Câu 40:

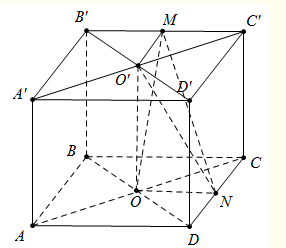
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a . Gọi O và O' lần lượt là tâm các hình vuông. Gọi Mvà N lần lượt là trung điểm của các cạnh B' C' và CD. Tính thể tích khối tứ diện OO'MN.

A. $\frac{a^{3}}{8}$

B. $a^{3}$

C. $\frac{a^{3}}{12}$

D. $\frac{a^{3}}{24}$

Xem đáp án

Đáp án D

$\begin{array}{l} S_{O' O N} = \frac{1}{2} OO'.ON= \frac{1}{2} . a . \frac{a}{2} = \frac{a^{2}}{4}; M O' = \frac{a}{2} . \\ V_{M O' O N} = \frac{1}{3} M O' . S_{O' O N} = \frac{a^{3}}{24} . \end{array}$

Câu 41:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích bằng 1. Trên cạnh SC lấy điểm E sao choSE=2EC. Tính thể tích V của khối tứ diện S.EBD.

A. $V = \frac{2}{3}$

B. $V = \frac{1}{6}$

C. $V = \frac{1}{3}$

D. $V = \frac{4}{3}$

Xem đáp án

Đáp án C

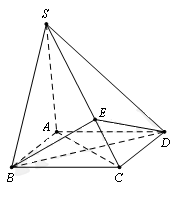
Ta có: $\frac{d (C; (S B D))}{d (E; (S B D))} = \frac{S C}{S E} = \frac{3}{2}$

$\Rightarrow d (C; (S B D)) = \frac{3}{2} d (E; (S B D)) .$

Mặt khác:

$V_{S . B C D} = \frac{1}{3} . d (C; (S B D)) . S_{Δ S B D} = \frac{1}{3} . \frac{3}{2} d (E; (S B D)) . S_{Δ S B D} .$

$\Rightarrow V_{B S B D} = \frac{2}{3} x V_{S . B C D}$

$\Leftrightarrow V_{S . E B D} = \frac{2}{3} . \frac{1}{2} x V_{S . A B C D} = \frac{1}{3} x V_{S . A B C D} = \frac{1}{3} .$

Câu 42:

Thể tích của khối lăng trụ tứ giác đều ABCDA'B'C'D' có tất cả các cạnh bằng a là

A. $3 a^{3}$

B. $\frac{a^{3} \sqrt{3}}{2}$

C. $a^{3}$

D. $\frac{a^{3} \sqrt{3}}{4}$

Xem đáp án

Đáp án C

Thể tích khối lăng trụ cần tính là: $V = A A' . S_{A B C D} = a . a^{2} = a^{3} .$

Câu 43:

Công thức tính thể tích khối trụ có bán kính đáy bằng R và chiều cao bằng h là

A. $V = π R h$

B. $V = π R^{2} h$

C. $V = \frac{1}{3} π R^{2} h$

D. $V = π R h^{2}$

Xem đáp án

Đáp án B

Thể tích khối trụ cần tính là $V = π R^{2} h$

Câu 44:

Thiết diện qua trục của một hình nón là một tam giác đều cạnh có độ dài 2a. Thể tích của khối nón là

A. $\frac{π a^{3} \sqrt{3}}{6}$

B. $\frac{π a^{3} \sqrt{3}}{3}$

C. $\frac{π a^{3} \sqrt{3}}{2}$

D. $\frac{π a^{3} \sqrt{3}}{12}$

Xem đáp án

Đáp án B

Khối nón giả thiết cho có bán kính đáy r=a chiều cao $h = 2 a . \frac{\sqrt{3}}{2} = a \sqrt{3} .$

Vậy thể tích của khối nón cần tính là $V = \frac{1}{3} π r^{2} h = \frac{1}{3} π a^{2} . a \sqrt{3} = \frac{π a^{3} \sqrt{3}}{3} .$

Câu 45:

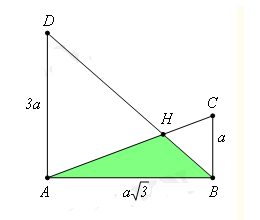
Cho tứ diện ABCD có $A D ⊥ (A B C),$ ABC là tam giác vuông tại B. Biết $B C = a, A B = a \sqrt{3}, A D = 3 a .$ Quay các tam giác ABC và ABD xung quanh đường thẳng AB ta được 2 khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng

A. $\frac{3 \sqrt{3} π a^{3}}{16}$

B. $\frac{8 \sqrt{3} π a^{3}}{3}$

C. $\frac{5 \sqrt{3} π a^{3}}{16}$

D. $\frac{4 \sqrt{3} π a^{3}}{16}$

Xem đáp án

Đáp án A

Vì hai mặt phẳng (ABC), (ABD) vuông góc với nhau nên bài toán trở thành “Tính thể tích khối tròn xoay khi quay tam giác HAB quanh AB với ABCD là hình thang vuông tại A,B” như hình bên. Hai tam giác BHC và DHA đồng dạng $\Rightarrow \frac{B H}{D H} = \frac{H C}{H A} = \frac{B C}{A D} = \frac{1}{3} .$

Mà $B D = \sqrt{A D^{2} + A B^{2}} = 2 a \sqrt{3}; A C = \sqrt{A B^{2} + C B^{2}} = 2 a$

Suy ra $A H = \frac{3}{4} A C = \frac{3}{4} .2 a = \frac{3 a}{2}$ và $B H = \frac{1}{4} B D = \frac{1}{4} .2 a \sqrt{3} = \frac{a \sqrt{3}}{2} .$

Diện tích tam giác ABH là:

$S_{Δ A B H} = \frac{1}{2} . A H . B H = \frac{1}{2} . \frac{3 a}{2} . \frac{a \sqrt{3}}{2} = \frac{3 a^{2} \sqrt{3}}{8} = \frac{1}{2} . d (H; B C) . B C \Rightarrow d (H; B C) = 2. \frac{3 a^{2} \sqrt{3}}{8} . a \sqrt{3} = \frac{3 a}{4} .$

Vậy thể tích khối tròn xoay cần tính là:

$V = \frac{1}{3} π {(\frac{3 a}{4})}^{2} . a \sqrt{3} = \frac{3 \sqrt{3} π a^{2}}{16} .$

Câu 46:

Cho hình lăng trụ ABCA'B'C' có thể tích bằng V. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, A'C’, BB’. Thể tích của khối tứ diện CMNP bằng

A. $\frac{5}{24} V$

B. $\frac{V}{4}$

C. $\frac{7}{24} V$

D. $\frac{V}{3}$

Xem đáp án

Đáp án A

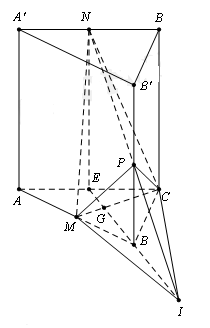
Gọi E là trung điểm của $A C \Rightarrow N E / / B B' .$ Nối NP cắt BE tại I suy ra B là trung điểm của EI. Gọi G là trọng tâm của tam giác ABC $\Rightarrow B G = 2 E G .$

$\Rightarrow d (B; M C) = 2 d (E; M C) \Rightarrow d (B; M C) = \frac{2}{3} d (B; A C)$

Suy ra: $d (I; M C) = (1 + \frac{3}{2}) d (B; M C) = \frac{5}{2} d (B; M C)$

Mà $S_{Δ I M C} = \frac{1}{2} d (I; M C) . M C$

$= \frac{1}{2} . \frac{5}{2} d (B; M C) . M C = \frac{5}{2} S_{Δ M B C} = \frac{5}{4} S_{Δ A B C}$

Ta có: $\frac{V_{N . M P C}}{V_{N . M I C}} = \frac{N P}{N I} = \frac{1}{2} \Rightarrow V_{N . M P C} = \frac{1}{2} x V_{N . M I C} (1)$

Lại có:

$\begin{array}{l} V_{N . M I C} = \frac{1}{3} . d (N; (A B C)) . S_{Δ I M C} = \frac{1}{3} . d (A'; (A B C)) . \frac{5}{4} S_{Δ A B C} \\ \Rightarrow V_{N . M I C} = \frac{5}{12} . d (A'; (A B C)) . S_{Δ A B C} \\ = \frac{5}{12} V_{A B C . A' B' C'} = \frac{5}{12} V \end{array}$

Từ (1) và (2) suy ra $V_{C M N P} = \frac{1}{2} . \frac{5}{12} x V = \frac{5}{24} V .$

Câu 47:

Cho mặt cầu có diện tích bằng $\frac{8 π a^{2}}{3}$ , bán kính của mặt cầu bằng

A. $\frac{a \sqrt{6}}{3}$

B. $\frac{a \sqrt{3}}{3}$

C. $\frac{a \sqrt{6}}{2}$

D. $\frac{a \sqrt{2}}{3}$

Xem đáp án

Đáp án A

Diện tích mặt cầu là:

$S = 4 π R^{2} = \frac{8 π a^{2}}{3} \Leftrightarrow R^{2} = \frac{2 a^{2}}{3} \Rightarrow R = \frac{a \sqrt{6}}{3} .$

Câu 48:

Có 4 viên bi hình cầu bán kính bằng 1 cm. Người ta đặt 3 viên bi tiếp xúc nhau và cùng tiếp xúc với mặt bàn. Sau đó đai chặt 3 viên bi đó lại và đặt 1 viên bi thứ tư tiếp xúc với cả 3 viên bi (hình vẽ dưới).

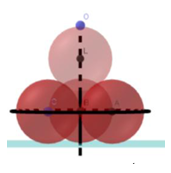
Gọi O là điểm thuộc bề mặt của viên bi thứ tư có khoảng cách đến mặt bàn là lớn nhất. Khoảng cách từ O đến mặt bàn bằng

A. $\frac{6 + 2 \sqrt{6}}{3}$

B. $\frac{7}{2}$

C. $\frac{3 + 2 \sqrt{6}}{3}$

D. $\frac{4 \sqrt{6}}{3}$

Xem đáp án

Đáp án A

Gọi A,B,C,D lần lượt là tâm của bốn hình cầu. Với B,C,D là tâm tứ diện đều cạnh 2cm có chiều cao $h = d (A; (B C D)) = \frac{2 \sqrt{6}}{3} c m .$

Khi đó, khoảng cách từ điểm đến mặt bàn là $d = h + 2 r = \frac{2 \sqrt{6}}{3} + 2 = \frac{6 + 2 \sqrt{6}}{3} .$

Câu 49:

Cho hình chóp S.ABCD có $\overset{⏜}{A B C} = \overset{⏜}{A D C} = 90^{\circ},$ cạnh bên SA vuông góc với mặt phẳng (ABCD), góc tạo bởi SC và mặt phẳng đáy bằng $60^{\circ}, C D = a$ và tam giác ADC có diện tích bằng $\frac{a^{2} \sqrt{3}}{2}$ . Diện tích mặt cầu $S_{m c}$ ngoại tiếp hình chóp S.ABCD là

A. $S_{m c} = 16 π a^{2}$

B. $S_{m c} = 4 π a^{2}$

C. $S_{m c} = 32 π a^{2}$

D. $S_{m c} = 8 π a^{2}$

Xem đáp án

Đáp án A

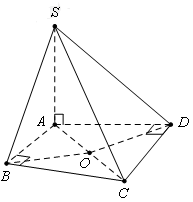
Tam giác ADC vuông tại D $\Rightarrow S_{Δ A D C} = \frac{1}{2} . A D . C D = \frac{a^{2} \sqrt{3}}{2}$

$\Rightarrow C D = a \sqrt{3} \Rightarrow A C = \sqrt{A D^{2} + C D^{2}} = \sqrt{a^{2} + {(a \sqrt{3})}^{2}} = 2 a .$

Vì tứ giác ABCD có $\overset{⏜}{A B C} = \overset{⏜}{A D C} = 90^{\circ} \Rightarrow A B C D$ là tứ giác nội tiếp đường tròn tâm O với O là trung điểm của AC $\Rightarrow R_{A B C D} = \frac{A C}{2} = a .$

Và $S A ⊥ (A B C D) \Rightarrow \overset{⏜}{S C; (A B C D)} = \overset{⏜}{(S C; A C)} = \overset{⏜}{S C A} = 60^{\circ}$

Tam giác SAC vuông tại A $\Rightarrow \tan \overset{⏜}{S C A} = \frac{S A}{A C} \Rightarrow S A = 2 a \sqrt{3} .$

Suy ra bán kính mặt cầu cần tính là:

$R = \sqrt{{R^{2}}_{A B C D} + \frac{S A^{2}}{4}} = 2 a \Rightarrow S_{m c} = 16 π a^{2} .$

Câu 50:

Trong không gian mặt cầu (S) tiếp xúc với 6 mặt của một hình lập phương cạnh a, thể tích khối cầu (S) bằng

A. $V = \frac{π a^{3}}{24}$

B. $V = \frac{π a^{3}}{3}$

C. $V = \frac{π a^{3}}{6}$

D. $V = \frac{4}{3} π a^{3}$

Xem đáp án

Đáp án C

Mặt cầu (S) chính là mặt cầu nội tiếp hình lập phương cạnh a $\Rightarrow R = \frac{a}{2} .$

Vậy thể tích khối cầu (S) là $V = \frac{4}{3} π R^{3} = \frac{4}{3} π . {(\frac{a}{2})}^{3} = \frac{π a^{3}}{6} .$