Tổng hợp 20 đề thi thử THPTQG môn Toán cực hay có đáp án (đề 11)
-
11904 lượt thi
-
50 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Trong các chữ cái “H, A, T, R, U, N, G” có bao nhiêu chữ cái có trục đối xứng.
 Xem đáp án
Xem đáp án
Đáp án A
Các chữ cái có trục đối xứng là : H, A,T, U
=> có tất cả 4 chữ cái có trục đối xứng
Câu 2:
Cho hàm số Tính diện tích S tam giác có ba đỉnh là ba điểm cực trị của đồ thị hàm số.
 Xem đáp án
Xem đáp án
Đáp án D
Ta có:
=> Các điểm cực trị là cân tại
Gọi I là trung điểm của
Ta có:
Cách 2: Áp dụng CT giải nhanh:
Câu 3:
Cho tứ diện ABCD và ba điểm M, N,P lần lượt nằm trên các cạnh AB, AC, AD mà không trùng với các đỉnh của tứ diện. Thiết diện của hình tứ diện ABCD khi cắt bởi mặt phẳng (MNP) là:
 Xem đáp án
Xem đáp án
Đáp án A
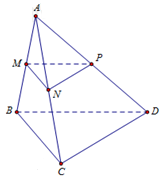
Thiết diện là
Câu 5:
Cho tứ diện đều cạnh a, điểm I nằm trong tứ diện. Tính tổng khoảng cách từ I đến tất cả các mặt của tứ diện.
 Xem đáp án
Xem đáp án
Đáp án A
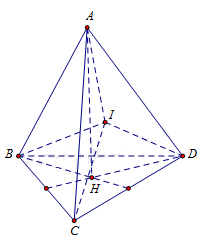
Gọi H là hình chiếu của A xuống (ABCD), Ta có:
Gọi S là diện tích 1 đáy và d là tổng khoảng cách từ I đến tất cả các mặt của tứ diện.
Ta có:
Câu 7:
Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng 0
 Xem đáp án
Xem đáp án
Đáp án B
Ta có hệ số góc của tiếp tuyến tại điểm có hoành độ bằng 0 là
Phương trình tiếp tuyến là
Câu 8:
Giải bóng chuyền VTV cup gồm 9 đội bóng trong đó có 6 đội nước ngoài và 3 đội của Việt Nam. Ban tổ chức cho bốc thăm ngẫu nhiên để chia thành 3 bảng A, B, C và mỗi bảng có ba đội. Tính xác suất để 3 đội bóng của Việt Nam ở 3 bảng khác nhau.
 Xem đáp án
Xem đáp án
Đáp án B
Số cách sắp ngẫu nhiên là (cách)
Số cách sắp để ba đội của Việt Nam ở 3 bảng khác nhau là: (cách)
Xác suất để 3 đội bóng của Việt Nam ở 3 bảng khác nhau là:
Câu 9:
Trong khoảng phương trình:
có bao nhiêu nghiệm?
 Xem đáp án
Xem đáp án
Đáp án B
Ta thấy không thỏa mãn phương trình
=> chia cả 2 vế của phương trình cho ta được:
Vì
nên
Câu 10:
Cho ba số thực dương x,y,z theo thứ tự lập thành một cấp số nhân, đồng thời với mỗi số thực dương thì theo thứ tự lập thành cấp số cộng.
Tính giá trị biểu thức
 Xem đáp án
Xem đáp án
Đáp án B
Vì theo thứ tự lập thành 1 CSN nên
Vì theo thứ tự lập thành cấp số cộng nên
Câu 11:
Tìm m để hàm số đồng biến trên khoảng
 Xem đáp án
Xem đáp án
Đáp án D
Đặt
Ta có
Hàm số đồng biến trên khoảng:
Câu 13:
Cho ba đường thẳng đôi một chéo nhau. Mệnh đề nào đúng trong các mệnh đề sau?
 Xem đáp án
Xem đáp án
Đáp án C
Lấy 1 điểm bất kỳ thuộc a và M ta dựng 2 mặt phẳng là giao tuyến của 2 mặt phẳng trên đi qua M và 2 điểm thuộc b và c. Vậy có vô số đường thẳng cắt cả ba đường thẳng đã cho.
Câu 15:
Gọi M,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số . Tính M,m.
 Xem đáp án
Xem đáp án
Đáp án A
Ta có:
PT (1) có nghiệm
Suy ra
Câu 16:
Từ các chữ số 0, 1, 2, 3, 4 lập được bao nhiêu số có năm chữ số khác nhau từng đôi một?
 Xem đáp án
Xem đáp án
Đáp án C
Gọi là số thỏa mãn đề bài, ta có
+) a có 4 cách chọn
+) b có 4 cách chọn
+) e có 3 cách chọn
+) d có 2 cách chọn
+) e có 1 cách chọn
Suy ra có cách chọn
Câu 19:
Cho hàm số y=f(x) xác định trên , liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ sau.
Tìm tập hợp tất cả các giá trị của tham số thực m sao cho phương trình f(x) = m có ba nghiệm phân biệt.
 Xem đáp án
Xem đáp án
Đáp án D
Câu 20:
Trung điểm của tất cả các cạnh của hình tứ diện đều là các đỉnh của khối đa diện nào?
 Xem đáp án
Xem đáp án
Đáp án B
Câu 21:
Trong mặt phẳng với hệ trục tọa độ Oxy cho đường tròn và . Phép đồng dạng F tỉ số k biến thành . Tìm k?
 Xem đáp án
Xem đáp án
Đáp án D
Ta có:
Câu 24:
Cho tứ diện ABCD gọi M, N lần lượt là trung điểm của BC và AD.
Biết . Tính góc giữa hai đường thẳng AB và CD.
 Xem đáp án
Xem đáp án
Đáp án C
Gọi P là trung điểm của AC.
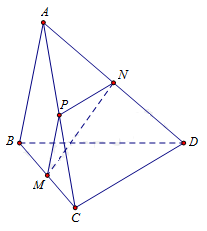
Ta có:
Câu 25:
Hàm số y = sin x đồng biến trên khoảng nào sau đây?
 Xem đáp án
Xem đáp án
Đáp án C
Hàm số đồng biến khi
<=> thuộc góc phần tư thứ 1 và 4
Câu 26:
Cho hàm số y=f(x) có đồ thị như hình vẽ.
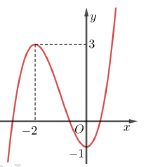
Tìm tập hợp tất cả các giá trị của m để đồ thị hàm số có 5 điểm cực trị.
 Xem đáp án
Xem đáp án
Đáp án D
Dựa vào đồ thị hàm số, dễ thấy hàm số
Xét hàm số với
Chú ý : Cực trị là điểm làm y' đổi dấu và
Do đó .
Khi đó có 5 điểm cực trị có 4 nghiệm phân biệt có 4 nghiệm
Cách 2: Đồ thị hàm số được suy ra từ
.
Đồ thị hàm số muốn có 5 điểm cực trị khi ở bước thứ 1ta dịch chuyển đồ thị sang phải nhiều hơn 2 đơn vị
Câu 27:
Cho tập hợp Hỏi có bao nhiêu cách lấy ra 5 số từ tập A sao cho không có hai số nào là hai số tự nhiên liên tiếp?
 Xem đáp án
Xem đáp án
Đáp án D
Nếu thì chỉ có duy nhất 1 cách là khi đó số cách bằng
Nếu thì có
có 6 cách bằng . Như vậy đáp án sẽ là
Câu 28:
Cho lăng trụ ABCA'B'C' có đáy ABC là tam giác vuông tại B, AB=a, BC=2a. Biết lăng trụ có thể tích tính khoảng cách d giữa hai đáy của lăng trụ theo a.
 Xem đáp án
Xem đáp án
Đáp án D
Câu 32:
Cho hình chóp S.ABCD có đáy là hình thang ABCD,AB//CD, AB=2AD. M là một điểm thuộc cạnh AD, là mặt phẳng qua M và song song với mặt phẳng (SAB). Biết diện tích thiết diện của hình chóp cắt bởi mặt phẳng bằng diện tích tam giác SAB. Tính tỉ số
 Xem đáp án
Xem đáp án
Đáp án A
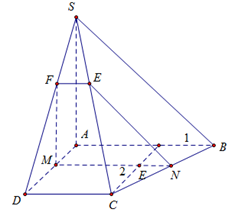
Câu 34:
Có bao nhiêu giá trị nguyên của m để phương trình có nghiệm.
 Xem đáp án
Xem đáp án
Đáp án D
Ta có:
Khi đó:
Lại có: do đó PT đã cho có nghiệm
có 9 giá trị nguyên của m
Câu 35:
Cho hình chóp S.ABC, G là trọng tâm tam giác ABC, A’, B’, C’ lần lượt là ảnh của A, B, C, qua phép vị tự tâm G tỉ số . Tính
 Xem đáp án
Xem đáp án
Đáp án A
Do là ảnh của qua phép
Do đó:
Câu 37:
Hàm số nào sau đây nghịch biến trên tập xác định?
 Xem đáp án
Xem đáp án
Đáp án B
Hàm số nghich biến trên khoảng
Câu 38:
Cho hình chóp S.ABCD có SD=x, tất cả các cạnh còn lại của hình chóp đều bằng a. Biết góc giữa SD và măt phẳng (ABCD) bằng . Tìm a.
 Xem đáp án
Xem đáp án
Đáp án D
Do S.ABC là hình chóp có SA=SB=SC nên hình chiếu vuông góc của đỉnh S xuống mặt đáy (ABC) trùng với tâm đường tròn ngoại tiếp O của (O thuộc trung trực BD)
Ta có:
Do đó vuông tại S
Khi đó:
Câu 39:
Đồ thị hai hàm số và cắt nhau tại hai điểm A,B. Tính độ dài đoạn thẳng AB.
 Xem đáp án
Xem đáp án
Đáp án B
Phương trình hoành độ giao điểm là:
Câu 40:
Cho hình chóp S.ABC có SA=a, SB=2a, SC=3a. Tìm giá trị lớn nhất của thể tích khối chóp S.ABC.
 Xem đáp án
Xem đáp án
Đáp án C
Khối chóp S.ABC có thể tích lớn nhất
Câu 42:
Tứ diện đều ABCD có cạnh bằng a. Tính khoảng cách giữa hai đường thẳng AB và CD
 Xem đáp án
Xem đáp án
Đáp án C
Gọi M, N lần lượt là trung điểm của AB, CD
Ta có: cân
Tương tự, ta chứng minh được là đoạn vuông chung của AB và
CD.
Xét tam giác ABN có:
Vậy khoảng cách giữa hai đường thẳng AB, CD là:
Câu 44:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với đáy (ABCD). Biết AB=a, BC=3a, SA=2a.Tính thể tích V của khối chóp S.ABCD.
 Xem đáp án
Xem đáp án
Đáp án B
Thể tích khối chóp S.ABCD là:
Câu 45:
Cho tứ diện ABCD có thể tích V. Gọi là tứ diện với các đỉnh lần lượt là trọng tâm tam giác BCD, CDA, DAB, ABC và có thể tích . Gọi là tứ diện với các đỉnh lần lượt là trọng tâm tam giác và có thể tích … cứ như vậy cho tứ diện có thể tích với n là số tự nhiên lớn hơn 1. Tính giá trị của biểu thức
 Xem đáp án
Xem đáp án
Đáp án A
Gọi M là trung điểm của AC và đặt độ dài AB = x
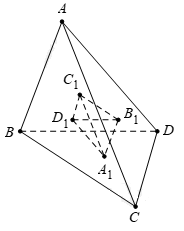
Vì là trọng tâm tam giác
Suy ra:
Tương tự, ta được là tứ diện đều cạnh
Khi đó
Suy ra
Tống S là tổng của cấp số nhân với:
Vậy
vì
Câu 46:
Trong các hàm số sau: có bao nhiêu hàm số có tập xác định là R?
 Xem đáp án
Xem đáp án
Đáp án C
Các hàm số xác định trên R là:
Câu 47:
Tìm tập hợp tất cả các giá trị của tham số m để đồ thị hàm số có đúng hai tiệm cận đứng ?
 Xem đáp án
Xem đáp án
Đáp án D
Đồ thị hàm số có 2 tiềm cận đứng
có 2 nghiệm phân biệt.
có 2 nghiệm phân biệt
Xét hàm số trên , có:
Tính cách giác trị và
Khi đó, yêu cầu Vậy là giá trị cần tìm
Câu 49:
Hàm số có đạo hàm trên khoảng .
Mệnh đề nào sau đây là sai ?
 Xem đáp án
Xem đáp án
Đáp án B
Câu B thiếu dấu bằng xảy ra tại hữu hạn điểm