Bộ 15 đề thi ôn vào lớp 6 môn Toán chất lượng cao năm 2024 - 2025 có đáp án (Đề 3)
-
58 lượt thi
-
16 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Điền số thích hợp vào chỗ trống: 50 cm2 × 8 + 6 dm2 = ….. dm2
Xem đáp án
50 cm2 × 8 + 6 dm2 = 400 cm2 + 6 dm2 = 4 dm2 + 6 dm2 = 10 dm2
Đáp số: 10
Câu 2:
Tính giá trị của biểu thức: 0,36 × 4 + 36% × 2 + 2 × 4 × 0,18
Xem đáp án
Ta có:
0,36 × 4 + 36% × 2 + 2 × 4 × 0,18
= 0,36 × 4 + 0,36 × 2 + 0,36 × 4
= 0,36 × (4 + 2 + 4)
= 0,36 × 10
= 3,6
Đáp số: 3,6
Câu 3:
Biết 5 người trong 3 ngày làm được 180 mét vải. Hỏi 7 người trong 2 ngày thì làm được bao nhiêu mét mải?
Xem đáp án
1 người trong 1 ngày làm được số mét vải là:
180 : 3 : 5 = 12 (m).
7 người trong 2 ngày thì làm được số mét vải là:
12 × 7 × 2 = 168 (m)
Đáp số: 168 mét
Câu 5:
Có 5 bao gạo tẻ và nếp nặng: 40kg, 48kg, 60kg. 44kg 25kg. Nếu lấy ra 1 bao gạo nếp thì lúc này số gạo tẻ gấp 3 lần số gạo nếp. Hỏi lúc đầu có bao nhiêu ki-lô-gam gạo nếp?
Xem đáp án
Tổng khối lượng của 5 bao gạo là:
40 + 48 + 60 + 44 + 25 = 217 (kg)
Sau khi lấy ra 1 bao gạo nếp thì lúc này số gạo tẻ gấp 3 lần số gạo nếp, tổng số gạo tẻ và gạo nếp là 4 phần. Suy ra tổng số gạo còn lại là một số chia hết cho 4.
Vi 217 : 4 = 54 (dư 1) nên số gạo nếp lấy ra phải là một số chia 4 dư 1.
Do đó, bao gạo nếp lấy ra nặng 25 ki-lô-gam.
Tổng số gạo còn lại sau khi lấy ra là:
217 – 25 = 192 (kg)
Lúc sau có số ki-lô-gam gạo nếp là:
192 : 4 × 1 = 48 (kg)
Lúc đầu có số ki-lô-gam gạo nếp là:
48 + 25 = 73 (kg)
Đáp số: 73 ki-lô-gam gạo nếp
Câu 6:
Khi bán một món đồ, dù giảm đi 10% so với giá bán ban đầu nhưng vẫn lãi 8% so với giá vốn. Hỏi nếu không giảm giá thì lãi bao nhiêu phần trăm?
Xem đáp án
Giả bán lúc sau chiếm số phần trăm giá bán ban đầu là:
100% - 10% = 90% (giá bán ban đầu)
Giá bán lúc sau chiếm số phần trăm giá vốn là:
100% + 8% = 108% (giá vốn)
Do đó: 90% giá bán ban đầu bằng 108% giá vốn.
Giá bán ban đầu chiếm số phần trăm so với giá vốn là:
103% : 90% = 120% (giá vốn)
Nếu không giảm giá thì sẽ lãi số phần trăm so với giá vốn là:
120% - 100% = 20% (giá vốn)
Đáp số: 20% giá vốn
Câu 7:
Phép chia 4,8 : 3,5 có thương là số thập phân có 2 chữ số sau dấu phẩy. Hỏi số dư của phép chia bằng bao nhiêu?
Xem đáp án
Thực hiện phép chia, ta có: 4,8 : 3,5 = 1,37 (dư 0,005)
Đáp số: 0,005
Câu 8:
Trường THCS Thanh Xuân tổ chức một chuyến đi tham quan. Tổng cộng có 454 học sinh đăng ký. Trường chia ra thành 2 loại xe chở học sinh, loại xe 29 học sinh và loại xe 35 học sinh. Biết các xe không chở thừa hay thiếu. Hỏi có bao nhiêu xe chở 35 học sinh? Biết tổng số xe là 14.
Xem đáp án
Giả sử 14 xe đều là loại xe chở 29 học sinh thì sẽ chở được tất cả số học sinh là:
29 × 14 = 406 (học sinh)
Số học sinh chênh lệch so với thực tế là:
454 – 406 = 48 (học sinh)
Mỗi lần thay 1 xe chở 35 học sinh thành 1 xe chở 29 học sinh thì số học sinh giảm đi là:
35 – 29 = 6 (học sinh)
Số xe chở 35 học sinh là:
48 : 6 = 8 (xe)
Đáp số: 8 xe
Câu 9:
Cùng cộng vào mẫu số và tử số của phân số ; một số tự nhiên đế bằng phân số . Tìm số tự nhiên đó.
Xem đáp án
Nếu cùng cộng vào mẫu số và tử số của phân số với cùng một số thì hiệu giữa mẫu số và tử số không thay đổi.
Hiệu của mẫu số và tử số là:
165 – 57 = 108
Lúc sau, tỉ số giữa tử số mới và mẫu số mới là
Tử số lúc sau là:
108 : (5 – 2) × 2 = 72
Số tự nhiên cần tìm là:
72 – 57 = 15
Đáp số: 15
Câu 10:
Có một cái bể đang chứa một số nước. Nếu thả một viên kim loại hình lập phương cạnh 10 cm thì sẽ chạm tới đáy bể, và mực nước dâng ngang mặt viên kim loại. Nếu thả một viên như thể có cạnh là 20 cm thì mực nước dâng cao 12 cm. Tính diện tích đáy bể.
Xem đáp án
Thể tích nước tăng thêm khi thả viên kim loại hình lập phương cạnh 10 cm là:
10 × 10 ×10 = 1000 (cm3).
Thể tích nước tăng thêm khi thả viên kim loại hình lập phương cạnh 20 cm là:
20 × 20 × 12 = 4800 (cm3).
Thể tích nước tăng thêm khi thả viên kim loại hình lập phương cạnh 20cm lớn hơn thể tích nước tăng thêm khi thả viên kim loại hình lập phương cạnh 10cm là:
4800 – 1000 = 3800 (cm3).
Diện tích đáy bể là
3800 : (12 – 10) = 1900 (cm3).
Đáp số: 1900 cm3
Câu 11:
Tính diện tích phần đã tô đậm trong hình vẽ sau:
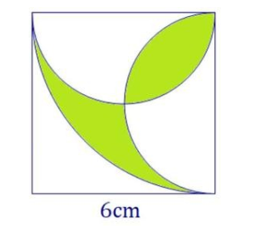
Xem đáp án
Nối thêm và đánh số các hình như sau:
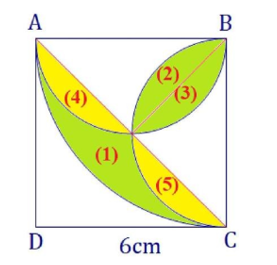
Quan sát hình vẽ, ta thấy: Diện tích các phần (2), (3), (4), (5) bằng nhau.
Do đó, tổng diện tích các phần (1), (2) và (3) chính bằng tổng diện tích các phần (1), (4) và (5) và bằng diện tích hình tròn bán kính BC trừ đi diện tích hình tam giác vuông ABC.
Diện tích hình tròn bán kính BC là: 6 × 6 × 3,14 = 113,04 (cm2).
diện tích hình tròn bán kính BC là: 113,04 : 4 = 28,26 (cm2).
Diện tích hình tam giác vuông ABC là: 6 × 6 : 2 = 18 (cm2).
Tổng diện tích các phần (1), (2), (3) là: 28,26 – 18 = 10,26 (cm2).
Vậy diện tích phần đã tô đậm là 10,26 cm2.
Đáp số: 10,26 cm2
Câu 13:
Tổng hai số lẻ là 504. Biết giữa hai số có 10 số lẻ khác. Tìm số lẻ bé.
Xem đáp án
Giữa 2 số lẻ có 10 số lẻ khác nữa nên có tất cả 12 số lẻ.
Giữa 12 số lẻ có 11 khoảng cách, mỗi khoảng cách là 2 đơn vị.
Hiệu 2 số lẻ đó là: 11 × 2 = 22.
Số lẻ bé là: (504 – 22) : 2 = 241.
Đáp số: 241.
Câu 14:
Xem đáp án
Số tự nhiên x lớn nhất thoả mãn 15,25 < x < 1 8,35 là: 18.
Đáp số: x = 18.
Câu 16:
Xe ô tô thứ nhất đi từ A đến B mất 6 tiếng, xe ô tô thứ hai đi từ A đến B mất 4 tiếng. Lúc 6 giờ 15 phút thì ô tô thứ nhất xuất phát từ A để đến B. Sau 2 giờ thì ô tô thứ hai xuất phát từ B để đến A. Hỏi 2 xe gặp nhau lúc mấy giờ.
Xem đáp án
Trong 1 giờ xe thứ nhất đi được: 1 : 6 = (quãng đường AB)
Trong 1 giờ xe thứ hai đi được: 1 : 4 = (quãng đường AB)
Trong 2 giờ xe thứ nhất đi được: (quãng đường AB)
Kể từ lúc xe thứ hai xuất phát, hai xe gặp nhau sau thời gian là:
(giờ) = 1 giờ 36 phút.
Hai xe gặp nhau lúc
6 giờ 15 phút + 2 giờ + 1 giờ 36 phút = 9 giờ 51 phút.