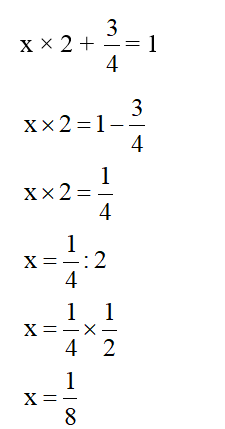Bộ 15 đề thi ôn vào lớp 6 môn Toán chất lượng cao năm 2024 - 2025 có đáp án (Đề 8)
-
63 lượt thi
-
13 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Xem đáp án
Hướng dẫn
Ta có: 123,4 + 1754 + 146,6 = (123,4 + 146,6) + 1754 = 270 + 1754 = 2024.
Câu 3:
Biết 15 người cùng làm thì hoàn thành một công việc trong 10 ngày. Hỏi nếu để hoàn thành công việc đó trong 5 ngày thì cần bao nhiêu người?
Xem đáp án
1 người làm thì hoàn thành công việc đó trong số ngày là:
10 × 15 = 150 (ngày).
Vậy để hoàn thành công việc đó trong 5 ngày thì cần số người là
150 : 5 = 30 (người).
Đáp số: 30 người.
Câu 4:
Tìm hai số, biết tổng của chúng là 104 và 5 lần số bé bằng 3 lần số lớn.
Xem đáp án
5 lần số bé bằng 3 lần số lớn
Hay: số bé bằng số lớn
Do đó, nếu coi số bé là 3 phần bằng nhau thì số lớn là 5 phần như thế.
Số bé là: 104: (3 + 5) × 3 = 39
Số lớn là 104 – 39 = 65
Đáp số: 39 và 65
Câu 5:
Cho hình lập phương có diện tích toàn phần là 294cm2. Tìm cạnh của hình lập phương đó.
Xem đáp án
Hướng dẫn
Diện tích một mặt của hình lập phương là:
294 : 6 = 49 (cm2).
Vì 7 × 7 = 49 nên cạnh của hình lập phương là 7 cm.
Đáp số: 7 cm.
Câu 6:
Cho các số 1; 2; 3; 4; 5. Hỏi có bao nhiêu số tự nhiên có 3 chữ số khác nhau có thể tạo thành từ các chữ số đã cho?
Xem đáp án
Lập số có 3 chữ số khác nhau từ các chữ số đã cho thì có:
5 cách chọn chữ số hàng trăm, 4 cách chọn chữ số hàng chục, 3 cách chọn chữ số hàng đơn vị.
Vậy có thể lập được số các số có 3 chữ số khác nhau từ các chữ số đã cho là:
5 × 4 × 3 = 60 (số).
Đáp số: 60 số.
Câu 7:
Minh viết các số tự nhiên liên tiếp từ 1. Khi viết xong Minh thấy mình đã viết được 207 chữ số. Hỏi Minh đã viết bao nhiêu số
Xem đáp án
Từ 1 đến 9 có 9 số có 1 chữ số nên Minh cần 9 chữ số để viết.
Từ 10 đến 99 có: (99 – 10) : 1 + 1= 90 (số có 2 chữ số)
→ Minh cần dùng số chữ số để viết các số này là:
2 × 90 = 180 (chữ số).
Các chữ số còn lại dùng để viết số có 3 chữ số là:
207 – 180 – 9 = 18 (chữ số).
Số các số có 3 chữ số Minh đã viết là: 18 : 3 = 6 (số).
Vậy số các số Minh đã viết là: 9 + 90 + 6 = 105 (số).
Đáp số: 105 số.
Câu 9:
dấu phẩy của số thập phân sang bên phải 1 hàng thì tổng mới là 26,5. Tìm số thập phân.
Xem đáp án
Nếu dịch chuyển dấu phẩy của số thập phân sang bên phải 1 hàng thì ta được số mới gấp 10 lần số thập phân ban đầu.
Do đó, tổng mới lớn hơn tổng ban đầu một số bằng 9 lần số thập phân ban đầu.
9 lần số thập phân ban đầu là: 26,5 – 7,15 = 19,35.
Số thập phân ban đầu là: 1935 : 9 = 2,15.
Đáp số: 2,15.
Câu 10:
Tìm tổng diện tích các phần tô đậm. Biết diện tích của mỗi hình tròn nhỏ bằng nhau và bán kính hình tròn nhỏ là 10cm.
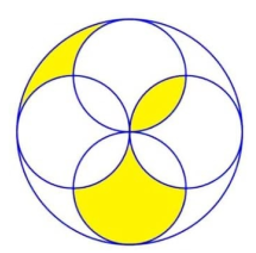
Xem đáp án
Ta nối thêm hình và đánh số thứ tự như sau:
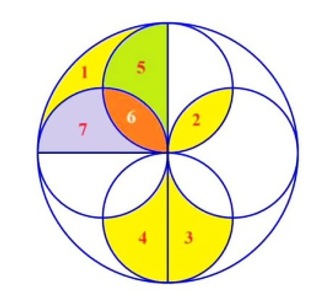
Quan sát hình vẽ ta thấy:
Tổng diện tích các phần tô đậm cần tính (1), (2), (3), (4) chính bằng tổng diện tích của các phần tô đậm (1), (6), (5), (7) và chính bằng diện tích hình tròn lớn.
Hình tròn lớn có bán kính bằng đường kính hình tròn nhỏ và bằng:
10 × 2 = 20 (cm)
Diện tích hình tròn lớn là:
20 × 20 × 3,14 = 1256 (cm2).
Vậy tổng diện tích các phần tô đậm cần tính (1) , (2), (3), (4) là:
1256 : 4 = 314 (cm2).
Đáp số: 314cm2.
Câu 11:
Một cửa hàng quần áo giảm giá 30% tất cả các sản phẩm. Một chiếc áo giá 300 000 đồng thì sau khi được giảm giá, người mua phải trả bao nhiêu tiền?
Xem đáp án
Khi mua chiếc áo đó, người mua được giảm số tiền là
300.000 : 100 × 30 = 90 000 (đồng).
Sau khi giảm giá, người mua phải trả số tiền khi mua chiếc áo đó là:
300 000 – 90.000 = 210 000 (đồng)
Đáp số: 210 000 đồng
Câu 12:
Cho hình thang ABCD có đáy nhỏ AB là 12cm, đáy lớn CD là 15cm và chiều cao bằng một nửa đáy nhỏ.
a) Tính diện tích hình thang ABCD.
b) Nối A với C, lấy M trên AC sao cho AC = 3 × AM. Tính diện tích tam giác MCD.
Xem đáp án
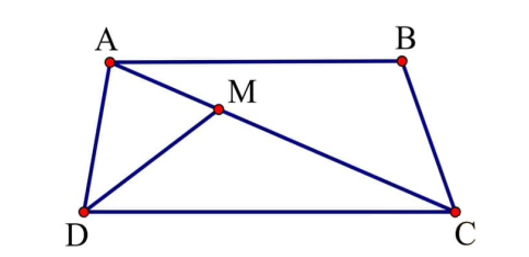
a) Chiều cao hình thang là: 12 : 2 = 6(cm).
Diện tích hình thang là: (12 +15) × 6 : 2 = 81 (cm2)
b) Chiều cao hạ từ A tới đáy DC của tam giác ADC bằng chiều cao của hình thang ABCD và bằng 6cm.
Diện tích tam giác ACD là: 15 × 6 : 2 = 45 (cm2).
Vì AC = 3 × AM nên MC = AC.
Diện tích tam giác MCD bằng diện tích tam giác ACD vì có chung chiều cao hạ từ D tới AC, đáy MC= AC.
Vậy diện tích tam giác MCD là: 45 × 2 : 3 = 30 (cm2).
Đáp số: a) 81cm2; b) 30cm2.
Câu 13:
Một giải bóng đá được tổ chức với thể lệ như sau. Ở vòng đấu loại, người ta chia ngẫu nhiên 4 đội vào một bảng đấu. Số đội dư ra (nếu có) sẽ vào một bảng đấu. Ở mỗi bảng, mỗi đội đều đấu với các đội khác 1 trận. Sau vòng đấu loại, sẽ chọn 2 đội có thành tích tốt nhất mỗi bảng tiến vào vòng đấu loại trực tiếp, các đội chia thành các cặp thi đấu một trận duy nhất để chọn đội thắng vào vòng loại trực tiếp thứ 2 và cứ thế đến khi chọn ra nhà vô địch. Giải bóng có 63 đội tham gia. Hỏi có bao nhiều trận đấu khi giải kết thúc?
Xem đáp án
Vì 63 : 4 = 15 (dư 3) nên với 63 đội tham gia có 16 bảng
- Với 15 bảng, mỗi bảng gồm 4 đội:
Trong mỗi bảng có số trận đấu là: 4 × 3 : 2 = 6(trận)
Có 15 bằng nên có 6 × 15 = 90 (trận).
- Với 1 bảng gồm 3 đội sẽ có số trận đấu là: 3 × 2 : 2 = 3 (trận).
Do đó, tổng số trận đấu ở vòng loại là: 90 + 3 = 93 (trận).
Sau vòng loại, mỗi bảng chọn ra 2 đội có thành tích tốt nhất để đấu nên chọn ra được tất cả 2 × 16 = 32 (đội) tham gia thi đấu.
32 đội này sẽ lập thành 16 cặp thi đấu nên có 16 trận.
Sau đó, chọn ra 16 đội thắng và lập thành 8 cặp thi đấu nên có 8 trận
Tiếp theo chọn ra 8 đội thắng và lập thành 4 cặp thi đấu nên có 4 trận.
Sau đó lại chọn ra 4 đội thắng và lập thành 2 cặp thi đấu nên có 2 trận.
Cuối cùng chọn ra 2 đội thắng thi đấu với nhau để tìm đội vô địch nên có 1 trận.
Vậy có tất cả số trận đấu khi giải kết thúc là:
93 + 16 + 8 + 4 + 2 + 1 = 124 (trận)
Đáp số: 124 trận