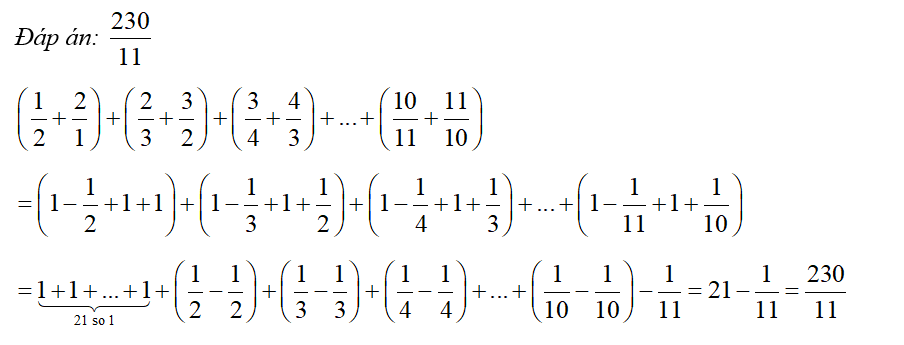Bộ 15 đề thi ôn vào lớp 6 môn Toán chất lượng cao năm 2024 - 2025 có đáp án (Đề 9)
-
388 lượt thi
-
10 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 3:
Lớp 6C1 của Archimedes có số học sinh ít hơn 35. Có số học sinh của lớp chơi bóng đá, học sinh xuống thư viện đọc sách, số học sinh chơi cầu lông. Hỏi bao nhiêu học sinh xuống thư viện đọc sách?
 Xem đáp án
Xem đáp án
Đáp án: 7 học sinh
Theo đề bài, ta có: Số học sinh của lớp 6C1 là một số chia hết cho 2, 4 và 7.
Các số tự nhiên khác 0 chia hết cho 2, 4 và 7 là: 28; 56; 84; ...
Mà lớp 6C1 có ít hơn 35 học sinh nên số học sinh lớp 6C1 là 28 học sinh.
Số học sinh xuống thư viện đọc sách là: 28 : 4 = 7 (học sinh).
Câu 4:
Có 4 con bạch tuộc A, B, C, D. Bạch tuộc có 6 hoặc 8 xúc tu luôn nói thật, bạch tuộc có 7 xúc tu luôn nói dối. Người ta hỏi các con bạch tuộc tổng số xúc tu là bao nhiêu? Các con bạch tuộc A, B, C, D lần lượt trả lời có 25, 26, 27, 28 xúc tu. Hỏi con nào nói thật?
 Xem đáp án
Xem đáp án
Đáp án: Bạch tuộc C
Vì tổng số xúc tu của 4 con bạch tuộc chỉ có đúng 1 phương án mà 4 con bạch tuộc có 4 kết quả khác nhau nên có ít nhất 3 con nói dối.
Giả sử 4 con nói dối. Khi đó, tổng số xúc tu của 4 con là:
7 × 4 = 28 (xúc tu).
→ Bạch tuộc D nói đúng → Mâu thuẫn → Loại
– Có 3 con nói dối, 1 con nói thật.
Tổng số xúc tu của 3 con nói dối là: 7 × 3 = 21 (xúc tu).
Con còn lại nói thật nên có 6 hoặc 8 xúc tu
Trường hợp con còn lại có 8 xúc tu:
Tổng số xúc tu của 4 con là:
21 + 8 = 29 (xúc tu)
→ Không có con nào nói đúng → Loại
Trường hợp con còn lại có 6 xúc tu:
Tổng số xúc tu của 4 con là:
21 + 6 = 27 (xúc tu).
→ Bạch tuộc C nói đúng, các bạch tuộc còn lại A, B, D nói sai
Câu 5:
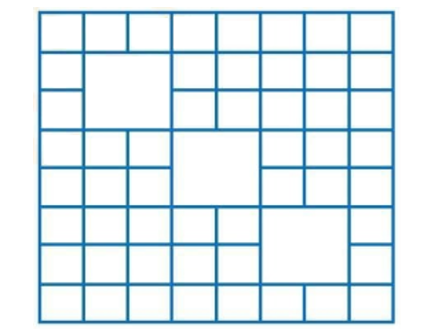
Cho tờ giấy hình vuông 8 × 8 bị cắt mất 3 hình vuông 2 × 2. Hỏi phải cắt như nào để được các hình chữ nhật 1 × 3 nhiều nhất có thể?
 Xem đáp án
Xem đáp án
Đáp án:
Hình còn lại có số ô vuông nhỏ là:
8 × 8 – 2 × 2 × 3 = 52 (ô vuông nhỏ).
Ta thấy để cắt được nhiều ô vuông 1 × 3 nhất ta cần cắt sao cho số ô vuông dư ra ít nhất có thể.
Ta không cắt được trường hợp ô vuông dư ra bằng 1.
Do đó ta cắt sao cho số ô vuông dư ra bằng 4 và cắt được nhiều nhất 16 hình chữ nhật 1 × 3.
Ví dụ cách cắt như sau:
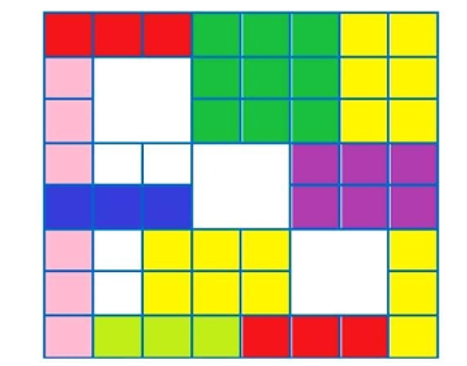
Câu 6:
Cho tam giác ABC tăng đáy 20%, giảm chiều cao tương ứng với đáy 15%. Hỏi diện tích tam giác ABC tăng hay giảm bao nhiêu phần trăm?
 Xem đáp án
Xem đáp án
Đáp án: tăng 2%
Độ dài đáy lúc sau bằng: 100% + 20% = 120% (độ dài đáy ban đầu)
Chiều cao tương ứng với đáy lúc sau bằng: 100% - 15% = 85% (chiều cao ban đầu)
Diện tích tam giác lúc sau bằng: 120% × 85% = 102% (diện tích tam giác ban đầu)
Diện tích tam giác lúc sau tăng số phần trăm so với diện tích tam giác lúc đầu là:
102% - 100% = 2% (diện tích tam giác lúc đầu).
Câu 7:
Cho số chia hết cho 8 số trong các số 1, 2, 3, 4, 5, 6, 7, 8, 9. Tìm tất cả các giá trị a, b.
Câu 8:
Cho các viên bi được đánh số từ 1 đến 99. Cần bốc ra ít nhất bao nhiêu viên bi để chắc chắn có 2 viên bi có tổng bằng 100?
 Xem đáp án
Xem đáp án
Đáp án: 51 viên bi
Ta có: 100 = 1 + 99 = 2 + 98 = ... = 49 + 51
99 : 2 = 49 (dư 1) nên nếu mỗi nhóm 2 viên bi ta nhóm được tất cả 49 nhóm và dư 1 viên bi.
Trường hợp xấu nhất, 49 viên bi đầu tiên lấy ra là 49 viên bi ở 49 nhóm (mỗi nhóm 1 viên bi), viên bi tiếp theo lấy ra là viên bi dư ra (viên bi không thuộc 49 nhóm trên).
Khi đó, để các viên bi lấy ra chắc chắn tồn tại 2 số có tổng là 100 ta cần lấy ra ít nhất:
49 + 1 + 1 = 51 (viên bị),
Đáp số: 51 viên bi.
Câu 9:
Người ta tô các số từ 1 đến 1000 màu đỏ hoặc xanh
a) Có thể tô các số có khoảng cách giữa 2 số là 5 và 9 các màu khác nhau?
b) Có thể tô các số có khoảng cách giữa 2 số là 8 và 11 các màu khác nhau?
 Xem đáp án
Xem đáp án
a) Giả sử các số có khoảng cách giữa 2 số là 5 và 9 được tô màu khác nhau.
Khi đó: Số a và a + 5 tô màu khác nhau. Số a và a + 9 tô màu khác nhau.
Do đó số a + 5 và a + 9 tô màu cùng nhau.
Hay hai số có khoảng cách bằng 4 tô màu cùng nhau.
Do đó số a và a + 4 tô màu cùng nhau.
Suy ra số a + 4 và a + 5 tô màu khác nhau. Hay hai số có khoảng cách bằng 1 tô màu khác nhau.
Do đó, số a và a + 1 tô màu khác nhau.
Vậy nếu cứ tô xen kẽ màu các số liên tiếp nhau thì các số có khoảng cách giữa 2 số là 5 và 9 được tô màu khác nhau.
b) Giả sử các số có khoảng cách giữa 2 số là 8 và 11 được tô màu khác nhau.
Khi đó:
Số a và a + 8 tô màu khác nhau.
Số a và a + 11 tô màu khác nhau.
Do đó a + 8 và a + 11 tô màu giống nhau.
Hay hai số có khoảng cách bằng 3 tô màu giống nhau.
Do đó, a và a + 3 tô màu giống nhau.
Suy ra a + 3 và a + 8 tô màu khác nhau.
Hay hai số có khoảng cách bằng 5 tô màu khác nhau.
Suy ra a và a + 5 tô màu khác nhau.
Suy ra a + 3 và a + 5 tô màu khác nhau.
Hay hai số có khoảng cách bằng 2 tô màu khác nhau.
Suy ra a và a + 2 tô màu khác nhau.
Suy ra a + 2 và a + 3 tô màu khác nhau.
Hay hai số có khoảng cách bằng 1 tô màu khác nhau.
Suy ra a và a + 1 tô màu khác nhau.
Suy ra a + 1 và a + 2 tô màu giống nhau (vì cả a + 1 và a + 2 đều tô màu khác a).
Hay hai số có khoảng cách bằng 1 tô màu giống nhau. Mâu thuẫn.
Vậy các số có khoảng cách giữa 2 số là 8 và 11 không thể được tô màu khác nhau.
Câu 10:
Tìm hai chữ số tận cùng của C biết
C = (1 + 2 + 3 + ... + 9) × (1 + 2 + 3 + ... + 9) × (1 + 2 + 3 + ... + 2024)
 Xem đáp án
Xem đáp án
Ta có:
C = (1 + 2 + 3 + ... + 9) × (1 + 2 + 3 + ... + 9) × (1 + 2 + 3 + ... + 2024)
Vì 2025 chia hết cho 25 và 1012 chia hết cho 4 mà tích của một số chia hết cho 25 và một số chia hết cho 4 là một số có 2 chữ số 0 ở tận cùng
Vậy C có hai chữ số tận cùng là 00.