(2023) Đề thi thử Vật Lí Sở GD Hà Tĩnh có đáp án
-
827 lượt thi
-
40 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Trong sự truyền sóng cơ, quãng đường sóng truyền được trong một chu kì gọi là
 Xem đáp án
Xem đáp án
\(\lambda = vT\), Chọn D
Câu 4:
Trong chân không, một ánh sáng đơn sắc có bước sóng \(\lambda \). Gọi \(h\) là hằng số Plăng, \(c\) là tốc độ ánh sáng trong chân không. Năng lượng của phôtôn ứng với ánh sáng đơn sắc này là
 Xem đáp án
Xem đáp án
\(\varepsilon = \frac{{hc}}{\lambda }\). Chọn C
Câu 8:
Hiện tượng chùm ánh sáng trắng đi qua lăng kính bị phân tách thành các chùm sáng đơn sắc là hiện tượng
 Xem đáp án
Xem đáp án
Chọn A
Câu 9:
Trong sơ đồ khối của máy phát thanh vô tuyến đơn giản không có bộ phận nào sau đây?
 Xem đáp án
Xem đáp án
Chọn B
Câu 10:
Đặt một điện áp xoay chiều có giá trị hiệu dụng không đổi, tần số góc \(\omega \) thay đổi được vào hai đầu một đoạn mạch gồm điện trở, cuộn cảm thuần có độ tự cảm \(L\) và tụ điện có điện dung \(C\) mắc nối tiếp. Cường độ dòng điện trong mạch cùng pha với điện áp hai đầu đoạn mạch khi
 Xem đáp án
Xem đáp án
Cộng hưởng. Chọn B
Câu 11:
Trên một sợi dây đang có sóng dừng. Sóng truyền trên dây có bước sóng \(\lambda \). Khoảng cách giữa hai nút sóng liên tiếp là
 Xem đáp án
Xem đáp án
Chọn B
Câu 12:
Cường độ dòng điện xoay chiều chạy qua một đoạn mạch có biểu thức \(i = {I_0}{\rm{cos}}\left( {\omega t + \varphi } \right)\). Cường độ dòng điện hiệu dụng trong mạch là
 Xem đáp án
Xem đáp án
Chọn D
Câu 13:
Một con lắc đơn có chiều dài \(l\), dao động điều hòa tại nơi có gia tốc trọng trường \(g\). Chu kì dao động của con lắc là
 Xem đáp án
Xem đáp án
Chọn D
Câu 16:
Đặt một điện áp xoay chiều \(u = 200\sqrt 2 {\rm{cos}}100\pi t\;\left( V \right)\) vào hai đầu một tụ điện có điện dung \(C\) thì cường độ dòng điện trong mạch là \(2\)A. Điện dung \(C\) của tụ điện có giá trị
 Xem đáp án
Xem đáp án
\({Z_C} = \frac{U}{I} = \frac{{200}}{2} = 100\Omega \)
\(C = \frac{1}{{\omega {Z_C}}} = \frac{1}{{100\pi .100}} = \frac{{{{10}^{ - 4}}}}{\pi }\) (F). Chọn D
Câu 17:
Hai dao động điều hòa cùng phương, cùng tần số, cùng biên độ \(4{\rm{\;cm}}\) và vuông pha với nhau. Biên độ dao động tổng hợp của hai dao động trên là
 Xem đáp án
Xem đáp án
\(A = \sqrt {A_1^2 + A_2^2} = \sqrt {{4^2} + {4^2}} = 4\sqrt 2 \) (cm). Chọn D
Câu 18:
Một mạch dao động \(LC\) lí tưởng đang có dao động điện từ tự do. Điện tích cực đại trên mỗi bản tụ là \({Q_0}\) và cường độ dòng điện cực đại trong mạch là \({I_0}\). Chu kỳ dao động điện từ của mạch là
 Xem đáp án
Xem đáp án
\(T = \frac{{2\pi }}{\omega } = \frac{{2\pi {Q_0}}}{{{I_0}}}\). Chọn D
Câu 19:
Cho một thấu kính hội tụ có tiêu cự \(10{\rm{\;cm}}\). Một điểm sáng \(S\) đặt trên trục chính của thấu kính và cách quang tâm của thấu kính \(15{\rm{\;cm}}\). Ảnh \(S\) ' của \(S\) qua thấu kính là
 Xem đáp án
Xem đáp án
\(\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f} \Rightarrow \frac{1}{{15}} + \frac{1}{{d'}} = \frac{1}{{10}} \Rightarrow d' = 30cm\). Chọn D
Câu 20:
Một bóng đèn sợi đốt có công suất tiêu thụ \(60{\rm{\;W}}\), được bật sáng trong thời gian 5 giờ. Điện năng tiêu thụ của bóng đèn trong thời gian trên là
 Xem đáp án
Xem đáp án
\(A = Pt = 60.5 = 300Wh = 0,3kWh\). Chọn D
Câu 22:
Hạt nhân \(\;_{55}^{142}{\rm{Cs}}\) có năng lượng liên kết là \(1179{\rm{MeV}}\), hạt nhân \(\;_{40}^{90}{\rm{Zr}}\) có năng lượng liên kết là \(784{\rm{MeV}}\), hạt nhân \(\;_{92}^{235}{\rm{U}}\) có năng lượng liên kết là \(1784{\rm{MeV}}\). Hãy sắp theo thứ tự tăng dần về tính bền vững của ba hạt nhân này.
 Xem đáp án
Xem đáp án
\(\varepsilon = \frac{{{W_{lk}}}}{A} \Rightarrow \left\{ \begin{array}{l}{\varepsilon _{Cs}} = \frac{{1179}}{{142}} \approx 8,3MeV\\{\varepsilon _{Zr}} = \frac{{784}}{{90}} \approx 8,7MeV\\{\varepsilon _U} = \frac{{1784}}{{235}} = 7,6MeV\end{array} \right. \Rightarrow {\varepsilon _U} < {\varepsilon _{Cs}} < {\varepsilon _{Zr}}\). Chọn B
Câu 23:
Một nguồn nhạc âm phát ra âm cơ bản có tần số \(200{\rm{\;Hz}}\). Tần số của họa âm thứ năm mà nhạc cụ có thể phát ra là
 Xem đáp án
Xem đáp án
\(f = 5{f_0} = 5.200 = 1000Hz\). Chọn B
Câu 24:
Cho phản ứng nhiệt hạch \(\;_1^2{\rm{H}} + \;_1^2{\rm{H}} \to \;_2^3{\rm{He}} + \;_0^1n\). Biết khối lượng nguyên tử của \(\;_1^2{\rm{H}};\;_2^3{\rm{He}};\;_0^1n\) lần lượt là \(2,0135{\rm{u}};3,0149{\rm{u}};1,0087{\rm{u}}\) và \(1{\rm{u}} = 931,5{\rm{MeV}}/{{\rm{c}}^2}\). Năng lượng mà phản ứng này tỏa ra là
 Xem đáp án
Xem đáp án
\(\Delta E = \left( {{m_t} - {m_s}} \right){c^2} = \left( {2.2,0135 - 3,0149 - 1,0087} \right).931,5 = 3,167MeV\). Chọn B
Câu 26:
Một con lắc lò xo gồm lò xo nhẹ có độ cứng \(50{\rm{\;N}}/{\rm{m}}\) gắn với vật nặng có khối lượng \(m\). Con lắc dao động điều hòa với chu kì \(0,2{\rm{\;s}}\). Lấy \({\pi ^2} = 10\). Khối lượng \(m\) của vật nặng bằng
 Xem đáp án
Xem đáp án
\(T = 2\pi \sqrt {\frac{m}{k}} \Rightarrow 0,2 = 2\pi \sqrt {\frac{m}{{50}}} \Rightarrow m \approx 0,05kg = 50g\). Chọn A
Câu 27:
Một vật nhỏ dao động điều hòa dọc theo trục \({\rm{Ox}}\) với phương trình \(x = 5{\rm{cos}}\left( {3t + \pi } \right)\left( {{\rm{cm}}} \right),t\) tính bằng s. Gia tốc của vật có giá trị cực đại bằng
 Xem đáp án
Xem đáp án
\({a_{\max }} = {\omega ^2}A = {3^2}.5 = 45cm/{s^2} = 0,45m/{s^2}\). Chọn A
Câu 28:
Một sợi dây đàn hồi \(OA\) treo thẳng đứng, đầu \(O\) gắn vào nhánh của một âm thoa, đầu \(A\) thả tự do. Khi âm thoa rung với chu kì \(0,05{\rm{\;s}}\) thì trên dây có sóng dừng với 8 bụng sóng. Biết sóng truyền trên dây với tốc độ \(4{\rm{\;m}}/{\rm{s}}\). Chiều dài của dây là
 Xem đáp án
Xem đáp án
\(\lambda = vT = 4.0,05 = 0,2m\)
\(l = 7,5.\frac{\lambda }{2} = 7,5.\frac{{0,2}}{2} = 0,75m = 75cm\). Chọn C
Câu 29:
Một tấm pin Mặt Trời được chiếu bởi chùm sáng đơn sắc có tần số \({5.10^{14}}{\rm{\;Hz}}\). Mỗi giây có \({5.10^{20}}\) phôtôn đập vào tấm pin. Hiệu suất của pin là \(8,5{\rm{\% }}\). Công suất phát điện của tấm pin Mặt Trời này là
 Xem đáp án
Xem đáp án
\(N = \frac{{Pt}}{{hf}} \Rightarrow {5.10^{20}} = \frac{P}{{6,{{625.10}^{ - 34}}{{.5.10}^{14}}}} \Rightarrow P = 165,625W\)
\({P_{ci}} = HP = 0,085.165,625 \approx 14,1W\). Chọn A
Câu 30:
Mắc vào hai cực của acquy một điện trở \(20{\rm{\Omega }}\) thì cường độ dòng điện chạy qua điện trở bằng \(0,5\)A. Biết điện trở trong của acquy là \(1{\rm{\Omega }}\). Suất điện động của acquy là
 Xem đáp án
Xem đáp án
\(E = I\left( {R + r} \right) = 0,5\left( {20 + 1} \right) = 10,5\) (V). Chọn B
Câu 31:
 Xem đáp án
Xem đáp án
\(T = 2\pi \sqrt {\frac{l}{g}} \Rightarrow {T_1} = 2\pi \sqrt {\frac{{0,25}}{{{\pi ^2}}}} = 1s\) và \[{T_2} = 2\pi \sqrt {\frac{{0,64}}{{{\pi ^2}}}} = 1,6s\]
\(t = {n_1}.\frac{{{T_1}}}{2} = {n_2}.\frac{{{T_2}}}{4}\) với \({n_1}\) là số nguyên và \({n_2}\) là số nguyên lẻ
\( \Rightarrow t = {n_1}.\frac{1}{2} = {n_2}.\frac{{1,6}}{4} \Rightarrow \frac{{{n_1}}}{{{n_2}}} = \frac{4}{5} = \frac{{12}}{{15}} \Rightarrow \left\{ \begin{array}{l}{n_1} = 12\\{n_2} = 15\end{array} \right. \Rightarrow t = 6s\). Chọn B
Câu 32:
Đặt điện áp xoay chiều \(u = 120\sqrt 2 {\rm{cos}}100\pi t\;\left( V \right)\) vào hai đầu một đoạn mạch gồm một điện trở \(R\), một cuộn cảm có độ tự cảm \(L\) thay đổi được và một tụ điện có điện dung \(C\) mắc nối tiếp với nhau. Đồ thị biểu diễn sự phụ thuộc hệ số công suất của đoạn mạch vào độ tự cảm \(L\) như hình vė. Công suất cực đại của đoạn mạch có giá trị
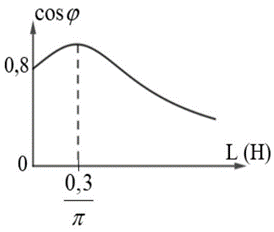
 Xem đáp án
Xem đáp án
Khi \(\cos {\varphi _{\max }} \Rightarrow \)cộng hưởng \( \Rightarrow {Z_C} = {Z_L} = \omega L = 100\pi .\frac{{0,3}}{\pi } = 30\Omega \)
Khi \({Z_L} = 0\) thì
\({P_{\max }} = \frac{{{U^2}}}{R} = \frac{{{{120}^2}}}{{40}} = 360\) (W). Chọn A
Câu 33:
Cho mạch điện như hình vẽ. Trong đó \({R_1} = 60{\rm{\Omega }},{R_2} = 20{\rm{\Omega }}\), cuộn dây thuần cảm có độ tự cảm thay đổi được. Độ lệch pha giữa điện áp hai đầu đoạn mạch \(AB\) và điện áp hai đầu đoạn mạch \(MB\) có giá trị lớn nhất là

 Xem đáp án
Xem đáp án
\(\tan \left( {{\varphi _{MB}} - {\varphi _{AB}}} \right) = \frac{{\tan {\varphi _{MB}} - \tan {\varphi _{AB}}}}{{1 + \tan {\varphi _{MB}}\tan {\varphi _{AB}}}} = \frac{{\frac{{{Z_L}}}{{{R_2}}} - \frac{{{Z_L}}}{{{R_1} + {R_2}}}}}{{1 + \frac{{{Z_L}}}{{{R_2}}}.\frac{{{Z_L}}}{{{R_1} + {R_2}}}}} = \frac{{{R_1}}}{{\frac{{{R_2}\left( {{R_1} + {R_2}} \right)}}{{{Z_L}}} + {Z_L}}}\mathop \le \limits_{{\mathop{\rm Cos}\nolimits} i} \frac{{{R_1}}}{{2\sqrt {{R_2}\left( {{R_1} + {R_2}} \right)} }}\)
\( \Rightarrow \tan \left( {{\varphi _{MB}} - {\varphi _{AB}}} \right) = \frac{{60}}{{2\sqrt {20\left( {60 + 20} \right)} }} \Rightarrow {\left( {{\varphi _{MB}} - {\varphi _{AB}}} \right)_{\max }} \approx 0,64\). Chọn A
Câu 34:
Trong thí nghiệm \(Y\)-âng về giao thoa ánh sáng, người ta sử dụng đồng thời hai bức xạ đơn sắc màu lam và màu đỏ có bước sóng lần lượt là \({\lambda _1} = 0,45\mu {\rm{m}};{\lambda _2} = 0,65\mu {\rm{m}}\). Số vân sáng màu lam nằm giữa hai vân sáng bậc 3 màu đỏ là
 Xem đáp án
Xem đáp án
\(3{\lambda _2} \approx 4,3{\lambda _1} \Rightarrow \)có \(4.2 = 8\) vân sáng màu lam. Chọn A
Câu 35:
Pôlôni \(\;_{84}^{210}\) Po là một chất phóng xạ có chu kì bán rã là \({\rm{T}} = 138\) ngày đêm. Hạt nhân pôlôni \(\;_{84}^{210}{\rm{Po}}\) phóng xạ sẽ biến đổi thành hạt nhân chì \(\;_{82}^{206}{\rm{\;Pb}}\) và kèm theo tia \(\alpha \). Ban đầu có \(35{\rm{mg}}\) chất phóng xạ pôlôni. Sau 276 ngày đêm khối lượng hạt nhân chì được sinh ra là
 Xem đáp án
Xem đáp án
\(\Delta N = {N_0}\left( {1 - {2^{\frac{{ - t}}{T}}}} \right) \Rightarrow \frac{{{m_{Pb}}}}{{206}} = \frac{{35}}{{210}}.\left( {1 - {2^{\frac{{ - 276}}{{138}}}}} \right) \Rightarrow {m_{Pb}} = 25,75mg\). Chọn A
Câu 36:
Tại điểm \(S\) trên mặt nước yên tĩnh có nguồn dao động điều hoà theo phương thẳng đứng với tần số \(f\). Khi đó trên mặt nước hình thành hệ thống sóng tròn đồng tâm \(S\). Ở mặt nước, hai điểm \(M\), \(N\) cách nhau \(10{\rm{\;cm}}\). trên đường thẳng đi qua \(S\) luôn dao động ngược pha với nhau. Biết tốc độ truyền sóng trên mặt nước là \(40{\rm{\;cm}}/{\rm{s}}\) và tần số của nguồn dao động có giá trị trong khoảng từ \(41{\rm{\;Hz}}\) đến \(51{\rm{\;Hz}}\). Tần số của nguồn dao động phát ra là
 Xem đáp án
Xem đáp án
Chọn D
Câu 37:
Ở mặt chất lỏng, tại hai điểm \(A\) và \(B\) cách nhau \(20{\rm{\;cm}}\) có hai nguồn sóng kết hợp dao động cùng pha theo phương thẳng đứng. Biết bước sóng là \(2{\rm{\;cm}}\). Nếu có một điểm sáng bắt đầu chuyển động tròn đều từ \(A\) trên đường tròn đường kính \(AB\) với tốc độ \(15,7{\rm{\;cm}}/{\rm{s}}\), thì thời gian ngắn nhất kể từ khi chuyển động đến khi điểm sáng cắt đường cực đại xa \(A\) nhất có giá trị gần nhất với giá trị nào sau đây?
 Xem đáp án
Xem đáp án
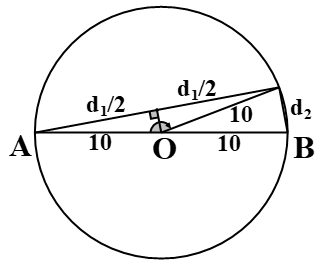
\(\frac{{AB}}{\lambda } = \frac{{20}}{2} = 10 \Rightarrow {d_1} - {d_2} = 9\lambda \Rightarrow {d_1} - \sqrt {{{20}^2} - d_1^2} = 9.2 \Rightarrow {d_1} \approx 19,91cm\)
\(R = \frac{{AB}}{2} = \frac{{20}}{2} = 10cm\)
\(\sin \frac{\alpha }{2} = \frac{{{d_1}/2}}{R} = \frac{{19,91/2}}{{10}} \Rightarrow \alpha \approx 2,95rad\)
\(s = R\alpha = \frac{{20}}{2}.2,95 = 29,5cm\)
\(t = \frac{s}{v} = \frac{{29,5}}{{15,7}} \approx 1,88s\). Chọn D
Câu 38:
Rađi \(\;_{88}^{226}\) Ra là nguyên tố phóng xạ \(\alpha \). Một hạt nhân \(\;_{88}^{226}\) Ra đang đứng yên phóng ra hạt \(\alpha \) và biến đổi thành hạt nhân con \({\rm{X}}\). Biết động năng của hạt \(\alpha \) là 4,5 \({\rm{MeV}}\). Lấy khối lượng hạt nhân tính theo đơn vị u bằng số khối của nó. Giả sử phóng xạ này không kèm theo bức xạ gamma. Năng lượng tỏa ra trong phân rã này là:
 Xem đáp án
Xem đáp án
\({}_{88}^{226}Ra \to {}_2^4\alpha + {}_{86}^{222}X\)
(MeV)
\(\Delta E = {K_\alpha } + {K_X} = 4,5 + \frac{3}{{37}} \approx 4,58\) (MeV). Chọn C
Câu 39:
Cho mạch điện như hình vẽ. Biết cuộn dây không thuần cảm có độ tự cảm \(L = \frac{{1,5}}{\pi }{\rm{H}}\), tụ điện có điện dung \(C = \frac{{{{10}^{ - 4}}}}{\pi }\) F. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \(u = 200\sqrt 2 {\rm{cos}}100\pi t\;\left( V \right)\), thì thấy khi \(k\) đóng và khi \(k\) mở, cường độ dòng điện trong mạch có cùng giá trị hiệu dụng \(I\) và vuông pha với nhau. Giá trị của \(I\) bằngCho mạch điện như hình vẽ. Biết cuộn dây không thuần cảm có độ tự cảm \(L = \frac{{1,5}}{\pi }{\rm{H}}\), tụ điện có điện dung \(C = \frac{{{{10}^{ - 4}}}}{\pi }\) F. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \(u = 200\sqrt 2 {\rm{cos}}100\pi t\;\left( V \right)\), thì thấy khi \(k\) đóng và khi \(k\) mở, cường độ dòng điện trong mạch có cùng giá trị hiệu dụng \(I\) và vuông pha với nhau. Giá trị của \(I\) bằng
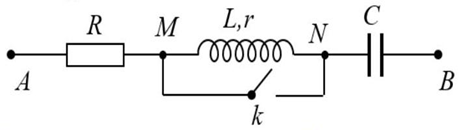
 Xem đáp án
Xem đáp án
\({Z_L} = \omega L = 100\pi .\frac{{1,5}}{\pi } = 150\Omega \) và \({Z_C} = \frac{1}{{\omega C}} = \frac{1}{{100\pi .\frac{{{{10}^{ - 4}}}}{\pi }}} = 100\Omega \)
\({i_d} \bot {i_m} \Rightarrow {\sin ^2}{\varphi _d} + {\sin ^2}{\varphi _m} = 1 \Rightarrow {\left( {\frac{{{Z_C}}}{{{Z_{RC}}}}} \right)^2} + {\left( {\frac{{{Z_L} - {Z_C}}}{Z}} \right)^2} = 1\) với \({Z_{RC}} = Z = \frac{U}{I} = \frac{{200}}{I}\)
\( \Rightarrow {\left( {\frac{{100}}{{200/I}}} \right)^2} + {\left( {\frac{{150 - 100}}{{200/I}}} \right)^2} = 1 \Rightarrow I \approx 1,79A\). Chọn C
Câu 40:
Một con lắc lò xo gồm lò xo nhẹ có độ cứng \(k = 100{\rm{\;N}}/{\rm{m}}\), đầu trên cố định, đầu dưới gắn với vật \({m_1}\) có khối lượng \(100{\rm{\;g}}\), vật \({m_2}\) có khối lượng \(300{\rm{\;g}}\) nối với \({m_1}\) bằng một sợi dây mềm, nhẹ, không dãn (Hình \({\rm{a}}\)). Ban đầu giữ vật \({m_1}\) ở vị trí lò xo không biến dạng, khi đó \({m_2}\) cách mặt đất một khoảng h. Bỏ qua lực cản không khí, lấy \(g = 10{\rm{\;m}}/{{\rm{s}}^2},{\pi ^2} = 10\). Thả nhẹ vật \({m_1}\) thì đồ thị li độ theo thời gian của \({m_1}\) ở khoảng thời gian đầu như hình \(b\). Giá trị của độ cao \(h\) bằng
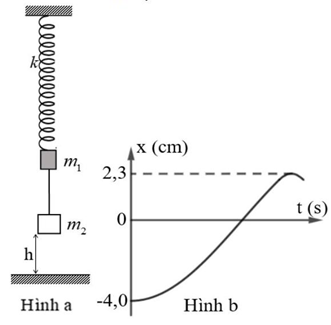
 Xem đáp án
Xem đáp án
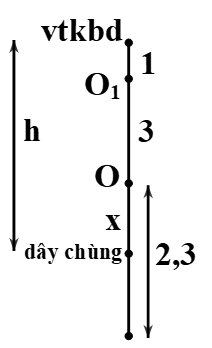
Cách 1: Lớp 12
GĐ1: Cả 2 vật cùng dao động điều hòa đến khi m2 chạm đất
\(A = \Delta {l_0} = \frac{{\left( {{m_1} + {m_2}} \right)g}}{k} = \frac{{\left( {0,1 + 0,3} \right).10}}{{100}} = 0,04m = 4cm\)
\(\omega = \sqrt {\frac{k}{{{m_1} + {m_2}}}} = \sqrt {\frac{{100}}{{0,1 + 0,3}}} = 5\sqrt {10} \) (rad/s)
GĐ2: Dây chùng, m1 dao động với vị trí cân bằng mới O1 dãn
\(\Delta {l_1} = \frac{{{m_1}g}}{k} = \frac{{0,1.10}}{{100}} = 0,01m = 1cm\)
\({\omega _1} = \sqrt {\frac{k}{{{m_1}}}} = \sqrt {\frac{{100}}{{0,1}}} = 10\sqrt {10} \) (rad/s)
\(v = {v_1} \Rightarrow \omega \sqrt {{A^2} - {x^2}} = {\omega _1}\sqrt {A_1^2 - x_1^2} \Rightarrow 5\sqrt {10} .\sqrt {{4^2} - {x^2}} = 10\sqrt {10} .\sqrt {{{\left( {2,3 + 3} \right)}^2} - {{\left( {x + 3} \right)}^2}} \)
\( \Rightarrow x \approx 2cm \Rightarrow h = 4 + x = 6cm\). Chọn C
Cách 2: Lớp 10
Chọn mốc thế năng tại vị trí lò xo không biến dạng
Bảo toàn cơ năng cho hệ vật từ vị trí lò xo không biến dạng đến khi \({m_2}\) chạm đất (dây chùng)
\(0 = \frac{1}{2}k{h^2} + \frac{1}{2}\left( {{m_1} + {m_2}} \right){v^2} - \left( {{m_1} + {m_2}} \right)gh \Rightarrow \frac{1}{2}\left( {{m_1} + {m_2}} \right){v^2} = \left( {{m_1} + {m_2}} \right)gh - \frac{1}{2}k{h^2}\) (1)
Bảo toàn cơ năng cho vật m1 từ khi m2 chạm đất (dây chùng) đến khi m1 xuống vị trí thấp nhất
\(\frac{1}{2}k{h^2} + \frac{1}{2}{m_1}{v^2} - {m_1}gh = \frac{1}{2}k{s^2} - {m_1}gs \Rightarrow \frac{1}{2}{m_1}{v^2} = {m_1}g\left( {h - s} \right) + \frac{1}{2}k\left( {{s^2} - {h^2}} \right)\) (2)
Quãng đường vật m1 đi từ vị trí lò xo không biến dạng đến vị trí thấp nhất là
\(s = 4 + 2,3 = 6,3cm = 0,063m\)
Lấy \(\frac{{\left( 1 \right)}}{{\left( 2 \right)}} \Rightarrow \frac{{{m_1} + {m_2}}}{{{m_1}}} = \frac{{\left( {{m_1} + {m_2}} \right)gh - \frac{1}{2}k{h^2}}}{{{m_1}g\left( {h - s} \right) + \frac{1}{2}k\left( {{s^2} - {h^2}} \right)}}\)
\( \Rightarrow \frac{{0,1 + 0,3}}{{0,1}} = \frac{{\left( {0,1 + 0,3} \right).10.h - \frac{1}{2}.100.{h^2}}}{{0,1.10.\left( {h - 0,063} \right) + \frac{1}{2}.100.\left( {0,{{063}^2} - {h^2}} \right)}} \Rightarrow h \approx 0,06m = 6cm\). Chọn C
