(2023) Đề thi thử Vật Lí Sở GD Vĩnh Phúc có đáp án
-
968 lượt thi
-
40 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Quá trình phóng xạ mà hạt nhân con có số proton tăng lên so với hạt nhân mẹ là
 Xem đáp án
Xem đáp án
\({}_Z^AX \to {}_{ - 1}^0e + {}_{Z + 1}^AY\). Chọn A
Câu 3:
Khi chiếu ánh sáng có bước sóng 600 nm vào một chất huỳnh quang thì bước sóng của ánh sáng phát quang do chất này phát ra không thể là
 Xem đáp án
Xem đáp án
Không thể nhỏ hơn 600 nm. Chọn C
Câu 4:
Trong mạch dao động điện từ tự do, biểu thức cường độ dòng điện trong mạch là \(i = 20{\rm{cos}}\left( {2000t + \pi /2} \right)\left( {mA} \right)\). Biểu thức điện tích của tụ điện trong mạch là
 Xem đáp án
Xem đáp án
\({Q_0} = \frac{{{I_0}}}{\omega } = \frac{{{{20.10}^{ - 3}}}}{{2000}} = {10^{ - 5}}C = 10\mu C\) và theo quy ước thì q trễ pha hơn i là \(\pi /2\). Chọn B
Câu 6:
Trong hiện tượng giao thoa sóng trên mặt nước, khoảng cách giữa điểm dao động với biên độ cực đại và điểm dao động với biên độ cực tiểu gần nhau nhất trên đoạn thẳng nối hai nguồn là
 Xem đáp án
Xem đáp án
Chọn A
Câu 8:
Một sóng cơ học có tần số \(f\) lan truyền trong môi trường vật chất đàn hồi với vận tốc v. Bước sóng của sóng đó là
 Xem đáp án
Xem đáp án
Chọn A
Câu 9:
Bên ngoài vỏ chai nước đóng chai có ghi "Bạn được bảo vệ nhờ hệ thống tiệt trùng UV", đó là ứng dụng của
 Xem đáp án
Xem đáp án
Chọn A
Câu 10:
Trong chân không, một ánh sáng đơn sắc có bước sóng \(\lambda \). Gọi h là hằng số Plăng c là tốc độ ánh sáng trong chân không. Năng lượng của photon ứng với ánh sáng đơn sắc này là
 Xem đáp án
Xem đáp án
\(\varepsilon = \frac{{hc}}{\lambda }\). Chọn C
Câu 11:
Chiếu một ánh sáng đơn sắc từ không khí vào một khối chất trong suốt với góc tới là \({45^ \circ }\) thì góc khúc xạ bằng \({30^ \circ }\). Chiết suất tuyệt đối của khối chất là
 Xem đáp án
Xem đáp án
\(\sin i = n\sin r \Rightarrow \sin {45^o} = n\sin {30^o} \Rightarrow n = \sqrt 2 \). Chọn A
Câu 12:
Đặt điện áp xoay chiều có tần số \(f\) vào hai đầu đoạn mạch chỉ có tụ điện có điện dung C. Đồ thị biểu diễn sự phụ thuộc của dung kháng \({Z_C}\) vào \(1/f\) là

 Xem đáp án
Xem đáp án
\({Z_C} = \frac{1}{{\omega C}} = \frac{1}{{2\pi C}}.\frac{1}{f}\). Chọn D
Câu 13:
Khi có dòng điện \(2{\rm{\;A}}\) chạy qua ống dây thì từ thông riêng gửi qua ống dây là 0,8 Wb. Hệ số tự cảm của ống dây là
 Xem đáp án
Xem đáp án
\(\phi = Li \Rightarrow 0,8 = L.2 \Rightarrow L = 0,4H\). Chọn B
Câu 14:
Từ thông qua một vòng dây dẫn có biểu thức \({\rm{\Phi }} = {2.10^{ - 2}}{\rm{cos}}\left( {100\pi t} \right)\left( {Wb} \right)\). Từ thông cực đại gửi qua vòng dây là
 Xem đáp án
Xem đáp án
\({\phi _0} = {2.10^{ - 2}}Wb\). Chọn B
Câu 17:
Trong thông tin liên lạc bằng sóng vô tuyến, mạch tách sóng ở máy thu thanh có tác dụng
 Xem đáp án
Xem đáp án
Chọn A
Câu 18:
Con lắc lò xo có độ cứng \(k = 20{\rm{\;N}}/{\rm{m}}\) và vật nhỏ có khối lượng m đang dao động cưỡng bức dưới tác dụng của ngoại lực \(F = 5{\rm{cos}}\left( {10t} \right)\left( N \right)\). Hệ dao động mạnh nhất khi khối lượng \({\rm{m}}\) bằng
 Xem đáp án
Xem đáp án
\(\omega = \sqrt {\frac{k}{m}} \Rightarrow 10 = \sqrt {\frac{{20}}{m}} \Rightarrow m = 0,2kg = 200g\). Chọn A
Câu 19:
Hạt nhân \(\;_2^4\) He có khối lượng 4,0015u, khối lượng các hạt proton và notron tương ứng là \({m_p} = 1,007276u,{m_n} = 1,008665u\). Độ hụt khối của hạt nhân \(\;_2^4{\rm{He}}\) là
 Xem đáp án
Xem đáp án
\(\Delta m = 2{m_p} + 2{m_n} - m = 2.1,007276 + 2.1,008665 - 4,0015 = 0,030382u\). Chọn C
Câu 20:
Một điện tích điểm \(q\) được đặt trong điện trường đều có véctơ cường độ điện trường \({\rm{\vec E}}\). Lực điện trường \(\vec F\) tác dụng lên điện tích điểm q được xác định theo công thức
 Xem đáp án
Xem đáp án
Chọn C
Câu 21:
Con lắc lò xo có khối lượng \(m\) dao động điều hòa với phương trình li độ \(x = A{\rm{cos}}\left( {\omega t + \varphi } \right)\). Thế năng cực đại của con lắc là
 Xem đáp án
Xem đáp án
\(W = \frac{1}{2}m\omega {}^2{A^2}\). Chọn B
Câu 22:
Đặt điện áp xoay chiều có giá trị hiệu dụng không đổi và tần số góc \(\omega \) thay đổi được vào hai đầu đoạn mạch gồm điện trở \(R\), cuộn cảm thuần có độ tự cảm \(L\) và tụ điện có điện dung \(C\) mắc nối tiếp. Điều kiện để công suất tiêu thụ của mạch đạt giá trị cực đại là
 Xem đáp án
Xem đáp án
Chọn A
Câu 23:
Một sóng cơ học lan truyền với bước sóng \(\lambda = 80{\rm{\;cm}}\). Độ lệch pha giữa hai điểm trên cùng phương truyền sóng có vị trí cân bằng cách nhau một khoảng \(40{\rm{\;cm}}\) là
 Xem đáp án
Xem đáp án
\(\Delta \varphi = \frac{{2\pi d}}{\lambda } = \frac{{2\pi .40}}{{80}} = \pi \). Chọn D
Câu 24:
 Xem đáp án
Xem đáp án
\(I = \frac{P}{{4\pi {r^2}}} \Rightarrow \frac{{{I_1}}}{{{I_2}}} = {\left( {\frac{{{r_2}}}{{{r_1}}}} \right)^2} = 4 \Rightarrow {r_2} = 2{r_1}\). Chọn A
Câu 25:
Một con lắc đơn khi vật nặng có khối lượng \(100{\rm{\;g}}\) thì dao động nhỏ với chu kì 2s. Khi khối lượng của vật là \(200{\rm{\;g}}\) thì chu kì dao động nhỏ của con lắc là
 Xem đáp án
Xem đáp án
\(T = 2\pi \sqrt {\frac{l}{g}} \) không đổi. Chọn D
Câu 28:
Nguồn laze mạnh phát ra những xung bức xạ có năng lượng W = 3000 J. Bức xạ phát ra bước sóng \(\lambda = 480{\rm{\;nm}}\). Lấy \({\rm{h}} = 6,{625.10^{ - 34}}{\rm{Js}};{\rm{c}} = {3.10^8}{\rm{\;m}}/{\rm{s}}\). Số proton phát ra trong mỗi xung bức xạ đó là
 Xem đáp án
Xem đáp án
\(N = \frac{W}{\varepsilon } = \frac{{W\lambda }}{{hc}} = \frac{{{{3000.480.10}^{ - 9}}}}{{1,{{9875.10}^{ - 25}}}} \approx 7,{25.10^{21}}\). Chọn A
Câu 29:
Dao động của một chất điểm có khối lượng \(50{\rm{\;g}}\) là tổng hợp của hai dao động điều hòa cùng phương có phương trình li độ lần lượt là \({x_1} = 5{\rm{cos}}10\pi t\;\left( {{\rm{cm}}} \right),{x_2} = 10{\rm{cos}}\left( {10\pi t + \pi /2} \right)\left( {{\rm{cm}}} \right)\). Lấy \({\pi ^2} = 10\). Lực kéo về cực đại tác dụng lên vật có giá trị bằng
 Xem đáp án
Xem đáp án
\(\Delta \varphi = \frac{\pi }{2} \Rightarrow A = \sqrt {A_1^2 + A_2^2} = \sqrt {{5^2} + {{10}^2}} = 5\sqrt 5 cm = 0,05\sqrt 5 m\)
\({F_{\max }} = m{\omega ^2}A = 0,05.{\left( {10\pi } \right)^2}.0,05\sqrt 5 \approx 5,6\) (N). Chọn C
Câu 30:
Một sóng điện từ đang lan truyền từ một đài phát sóng ở Vĩnh Phúc đến máy thu. Biết cường độ điện trường cực đại là \(20{\rm{\;V}}/{\rm{m}}\) và cảm ứng từ cực đại là \(0,6{\rm{\;T}}\). Tại điểm \({\rm{M}}\) có sóng truyền về hướng Nam, ở một thời điểm khi vectơ cảm ứng từ có độ lớn bằng \(0,15{\rm{\;T}}\) và đang hướng về phía Đông thì cường độ điện trường tại điểm \(M\) lúc đó có độ lớn và hướng như thế nào?
 Xem đáp án
Xem đáp án
\(\frac{E}{{{E_0}}} = \frac{B}{{{B_0}}} \Rightarrow \frac{E}{{20}} = \frac{{0,15}}{{0,6}} \Rightarrow E = 5V/m\)
Áp dụng quy tắc tam diện thuận. Chọn B
Câu 31:
Một con lắc lò xo treo thẳng đứng gồm vật nặng \({\rm{m}} = 100{\rm{\;g}}\), lò xo có độ cứng k = 40 \({\rm{N}}/{\rm{m}}\). Từ vị trí cân bằng kéo vật xuống dưới \(5{\rm{\;cm}}\) rồi thả nhẹ cho vật dao động điều hòa. Lấy \({\pi ^2} = \) \(10,{\rm{\;g}} = 10{\rm{\;m}}/{{\rm{s}}^2}\). Trong một chu kì tốc độ trung bình của vật trong khoảng thời gian lò xo bị nén là
 Xem đáp án
Xem đáp án
\(\Delta {l_0} = \frac{{mg}}{k} = \frac{{0,1.10}}{{40}} = 0,025m = 2,5cm = \frac{A}{2}\)
\(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{40}}{{0,1}}} = 20\) (rad/s)
\({v_{tb}} = \frac{s}{t} = \frac{A}{{\frac{\alpha }{\omega }}} = \frac{5}{{\frac{{2\pi /3}}{{20}}}} \approx 47,75cm/s\). Chọn B
Câu 32:
Theo mẫu nguyên tử Bohr, trong nguyên tử hiđro xem chuyển động của electron quanh hạt nhân là chuyển động tròn đều. Biết điện tích của electron là e = -1,6.10-19 \({\rm{C}}\), khối lượng electron là \({\rm{m}} = 9,{1.10^{ - 31}}{\rm{\;kg}}\), hằng số Culông \({\rm{k}} = {9.10^9}{\rm{N}}{{\rm{m}}^2}/{{\rm{C}}^2}\), bán kính Bohr là \({{\rm{r}}_0} = 5,{3.10^{ - 11}}{\rm{\;m}}\). Tốc độ của electron trên quỹ đạo \({\rm{M}}\) có giá trị gần nhất với giá trị nào sau đây?
 Xem đáp án
Xem đáp án
\(F = m{a_{ht}} \Rightarrow k.\frac{{{e^2}}}{{{r^2}}} = m.\frac{{{v^2}}}{r} \Rightarrow k.\frac{{{e^2}}}{{{n^2}{r_0}}} = m{v^2} \Rightarrow {9.10^9}.\frac{{{{\left( {1,{{6.10}^{ - 19}}} \right)}^2}}}{{{3^2}.5,{{3.10}^{ - 11}}}} = 9,{1.10^{ - 31}}.{v^2} \Rightarrow v \approx 728553m/s\)
Chọn B
Câu 33:
Một sợi dây đàn hồi căng ngang đang có sóng dừng ổn định. Trên dây \(A\) là một điểm nút, \(B\) là một điểm bụng gần \(A\) nhất, \(M\) là trung điểm của \(AB\) với \(AB = 18{\rm{\;cm}}\). Biết khoảng thời gian ngắn nhất giữa hai lần mà li độ dao động của phần tử tại \(B\) bằng biên độ dao động của phần từ tại \({\rm{M}}\) là \(0,3{\rm{\;s}}\). Tốc độ truyền sóng trên dây là
 Xem đáp án
Xem đáp án
\(AB = \frac{\lambda }{4} = 18cm \Rightarrow \lambda = 72cm\)
\(d = \frac{{AB}}{2} = \frac{\lambda }{8} \Rightarrow t = 2.\frac{T}{8} = 0,3s \Rightarrow T = 1,2s\)
\(v = \frac{\lambda }{T} = \frac{{72}}{{1,2}} = 60cm/s = 0,6m/s\). Chọn C
Câu 34:
Đặt điện áp \(u = 200\sqrt 2 {\rm{cos}}100\pi t\left( V \right)\) vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở \({\rm{R}} = 180{\rm{\Omega }}\), cuộn dây không thuần cảm và tụ điện có điện dung \({\rm{C}}\) thay đổi được. Khi \({\rm{C}} = {{\rm{C}}_1}\) thì dòng điện trong mạch có biểu thức \(i = {\rm{cos}}\left( {100\pi t + \pi /4} \right)\left( A \right)\). Khi \({\rm{C}} = {{\rm{C}}_2}\) thì điện áp hiệu dụng giữa hai đầu \({\rm{R}}\) đạt giá trị cực đại, giá trị cực đại đó bằng
 Xem đáp án
Xem đáp án
\(\frac{u}{i} = \frac{{200\sqrt 2 \angle 0}}{{1\angle \frac{\pi }{4}}} = 200 - 200j \Rightarrow R + r = 200\)
\({U_{R\max }} = \frac{{UR}}{{R + r}} = \frac{{200.180}}{{200}} = 180\) (V). Chọn D
Câu 35:
Dùng một hạt \(\alpha \) có động năng 7,7 \({\rm{MeV}}\) bắn vào hạt nhân \(\;_7^{14}{\rm{\;N}}\) đang đứng yên gây ra phản ứng \(\alpha + \;_7^{17}N \to _1^1p + \;_8^{17}{\rm{O}}\). Hạt proton bay ra theo phương vuông góc với phương bay tới của hạt \(\alpha \). Cho khối lượng các hạt \({{\rm{m}}_\alpha } = 4,0015{\rm{u}};{{\rm{m}}_{\rm{p}}} = 1,0073{\rm{u}};{m_{\rm{N}}} = 13,9992{\rm{u}};{m_{{{\rm{O}}_{17}}}} = 16,9947\) u và 1u \( = 931,5{\rm{MeV}}/{{\rm{c}}^2}\). Động năng của hạt nhân \(\;_8^{17}{\rm{O}}\) là
 Xem đáp án
Xem đáp án
\(\Delta E = \left( {{m_t} - {m_s}} \right){c^2} = {K_p} + {K_O} - {K_\alpha }\)
\( \Rightarrow \left( {4,0015 + 13,9992 - 1,0073 - 16,9947} \right).931,5 = {K_P} + {K_O} - 7,7 \Rightarrow {K_P} = 6,48905 - {K_O}\)
\( \Rightarrow 16,9947.{K_O} = 4,0015.7,7 + 1,0073.\left( {6,48905 - {K_O}} \right) \Rightarrow {K_O} \approx 2,075MeV\). Chọn D
Câu 36:
Điện năng được truyền từ nơi phát đến một khu dân cư bằng đường dây một pha với hiệu suất truyền tải là \(85{\rm{\% }}\). Coi hao phí điện năng chỉ do tỏa nhiệt trên đường dây và không vượt quá 25%. Nếu công suất sử dụng điện của khu dân cư này tăng 30% và giữ nguyên điện áp ở nơi phát thì hiệu suất truyền tải điện năng trên đường dây đó là
 Xem đáp án
Xem đáp án
|
\(P\) |
\(\Delta P\) |
\({P_{tt}}\) |
|
\(1/0,85\) (2) |
\(1/0,85 - 1\) (3) |
1 (1) |
|
\(1,3/H\) (5) |
\(1,3/H - 1,3\) (6) |
1,3 (4) |
\[U = \frac{P}{{\sqrt {\frac{{\Delta P}}{R}} \cos \varphi }} \Rightarrow \frac{{{U_2}}}{{{U_1}}} = \frac{{{P_2}}}{{{P_1}}}\sqrt {\frac{{\Delta {P_1}}}{{\Delta {P_2}}}} \Rightarrow 1 = \frac{{1,3/H}}{{1/0,85}}\sqrt {\frac{{1/0,85 - 1}}{{1,3/H - 1,3}}} \Rightarrow H \approx 0,79 = 79\% \]. Chọn A
Câu 37:
Một con lắc lò xo dao động điều hòa trên mặt phẳng nằm ngang. Công suất \({\rm{P}}\) được xác định bởi tích của lực kéo về và vận tốc của vật là đại lượng đặc trưng cho tốc độ chuyển hóa giữa thế năng và động năng. Hình bên là đồ thị biểu diễn sự phụ thuộc của \(P\) theo thời gian t. Tại thòi điểm ban đầu \(t = 0\), vật cách vị trí cân bằng \(5{\rm{\;cm}}\). Độ cứng của lò xo là
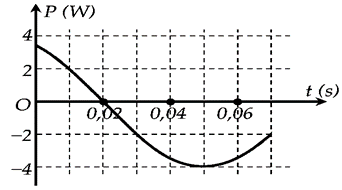
 Xem đáp án
Xem đáp án
\[p = Fv = kA\cos \left( {\omega t + \varphi } \right).\omega A\sin \left( {\omega t + \varphi } \right) = \frac{1}{2}k\omega {A^2}\sin \left( {2\omega t + 2\varphi } \right)\] (1)
\(\frac{{T'}}{4} = 3\^o = 0,03s \Rightarrow T' = 0,12s \Rightarrow \omega ' = \frac{{2\pi }}{{T'}} = \frac{{50\pi }}{3}rad/s\)
\(p = 4\cos \left( {\frac{{50\pi }}{3}(t - 0,02) + \frac{\pi }{2}} \right) = 4\cos \left( {\frac{{50\pi }}{3}t + \frac{\pi }{6}} \right) = 4\sin \left( {\frac{{50\pi }}{3}t + \frac{{2\pi }}{3}} \right)\) (2)
Đồng nhất (1) và (2) được \(\omega = \frac{{25\pi }}{3}rad/s\) và \[\left| x \right| = \left| {A\cos \varphi } \right| = \frac{A}{2} = 5cm \Rightarrow A = 10cm = 0,1m\]
\[\frac{1}{2}k\omega {A^2} = 4 \Rightarrow \frac{1}{2}k.\frac{{25\pi }}{3}.0,{1^2} = 4 \Rightarrow k \approx 30,6\] (N/m). Chọn A
Câu 38:
Trên mặt chất lỏng có hai nguồn kết hợp \({S_1}\) và \({S_2}\) cách nhau \(15{\rm{\;cm}}\) dao động theo phương thẳng đứng với phương trình \({u_1} = {u_2} = 2\cos 10\pi t\left( {{\rm{mm}}} \right)\). Tốc độ truyền sóng trên mặt chất lỏng là \(20{\rm{\;cm}}/{\rm{s}}\). Coi biên độ sóng không đổi khi truyền đi. Điểm \(M\) trong môi trường cách các nguồn những khoảng \({M_1} = 25{\rm{\;cm}}\) và \({M_2} = 20{\rm{\;cm}}\). Hai điểm \(A\) và \(B\) nằm trên đoạn \({S_2}M\) với \(A\) gần \({S_2}\) nhất, \(B\) xa \({S_2}\) nhất đều có tốc độ dao động cực đại bằng \(40\pi \;{\rm{mm}}/{\rm{s}}\). Khoảng cách \({\rm{AB}}\) bằng
 Xem đáp án
Xem đáp án
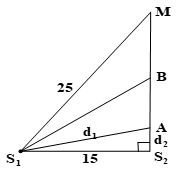
\(A = \frac{{{v_{\max }}}}{\omega } = \frac{{40\pi }}{{10\pi }} = 4cm = 2a \to \)cực đại
\(\lambda = v.\frac{{2\pi }}{\omega } = 20.\frac{{2\pi }}{{10\pi }} = 4cm\)
Trên \(M{S_2}\) thì \(\frac{{M{S_1} - M{S_2}}}{\lambda } < k < \frac{{{S_1}{S_2}}}{\lambda } \Rightarrow \frac{{25 - 20}}{4} < k < \frac{{15}}{4}\)
\( \Rightarrow 1,25 < k < 3,75 \Rightarrow k = 2;3\)
\({d_1}^2 - {d_2}^2 = {S_1}{S_2}^2 \Rightarrow \left\{ \begin{array}{l}{d_1} - {d_2} = k\lambda \\{d_1} + {d_2} = \frac{{{S_1}{S_2}^2}}{{k\lambda }}\end{array} \right. \Rightarrow {d_2} = \frac{{{S_1}{S_2}^2}}{{2k\lambda }} - \frac{{k\lambda }}{2} = \frac{{{{15}^2}}}{{2k.4}} - \frac{{k.4}}{2} \Rightarrow \left\{ \begin{array}{l}k = 2 \Rightarrow {d_2} = 10,0625cm\\k = 3 \Rightarrow {d_2} = 3,375cm\end{array} \right.\)
Vậy \(AB = 10,0625 - 3,375 = 6,6875\). Chọn D
Câu 39:
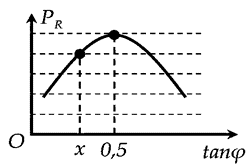
Đặt điện áp \(u = U\sqrt 2 {\rm{cos}}\omega t\) (U; \(\omega \) không đổi) vào hai đầu đoạn mạch mắc nối tiếp gồm biến trở \(R\), cuộn dây không thuần cảm và tụ điện. Gọi \(\varphi \) là độ lệch pha giữa hai đầu đoạn mạch và cường độ dòng điện trong mạch; \({P_R}\) là công suất tỏa nhiệt trên \(R\). Hình vẽ bên là một phần đồ thị biểu diễn mối liên hệ giữa \({P_R}\) và \({\rm{tan}}\varphi \). Giá trị của \(x\) bằng
 Xem đáp án
Xem đáp án
\({P_{R\max }} \Leftrightarrow {R_0} = {Z_{rLC}} = 1\) (chuẩn hóa) \( \Rightarrow {r^2} + Z_{LC}^2 = 1\) (1)
Ta có \(\tan {\varphi _0} = \frac{{{Z_{LC}}}}{{{R_0} + r}} \Rightarrow 0,5 = \frac{{{Z_{LC}}}}{{1 + r}}\) (2)
Từ (1) và (2) \( \Rightarrow \left\{ \begin{array}{l}r = 0,6\\{Z_{LC}} = 0,8\end{array} \right.\)
Khi \({P_R} = \frac{4}{5}{P_{R\max }} \Rightarrow \frac{{{U^2}R}}{{{{\left( {R + r} \right)}^2} + Z_{LC}^2}} = \frac{4}{5}\frac{{{U^2}{R_0}}}{{{{\left( {{R_0} + r} \right)}^2} + Z_{LC}^2}}\)
\( \Rightarrow \frac{R}{{{{\left( {R + 0,6} \right)}^2} + 0,{8^2}}} = \frac{4}{5}\frac{1}{{{{\left( {1 + 0,6} \right)}^2} + 0,{8^2}}} \Rightarrow R \approx 2,38\)
Vậy \(x = \frac{{{Z_{LC}}}}{{R + r}} = \frac{{0,8}}{{2,38 + 0,6}} \approx 0,268\). Chọn A
Câu 40:
Thí nghiệm giao thoa Y-âng với ánh sáng đơn sắc có bước sóng \(\lambda = 0,75\mu {\rm{m}}\), khoảng cách giữa hai khe là \({\rm{a}} = 1{\rm{\;mm}}\), khoảng cách từ hai khe đến màn quan sát là \({\rm{D}} = 2{\rm{\;m}}\). Tại thời điểm \(t = 0\), truyền cho màn vận tốc ban đầu hướng về phía hai khe để màn dao động điều hòa với chu kì 3 s và biên độ \(40{\rm{\;cm}}\). Thời điểm lần thứ 2023 điểm \(M\) trên màn cách vân trung tâm 19,8 mm trở thành vân sáng gần nhất với giá trị nào sau đây?
 Xem đáp án
Xem đáp án
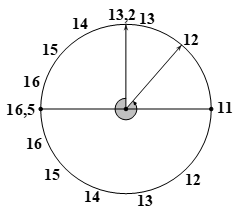
\(x = ki = k.\frac{{\lambda \left( {D + u} \right)}}{a} \Rightarrow 19,8 = k.\frac{{0,75.\left( {2 + u} \right)}}{1} \Rightarrow \left\{ \begin{array}{l}u = 0 \to k = 13,2\\u = - A = - 0,4m \to k = 16,5\\u = A = 0,4m \to k = 11\end{array} \right.\)
\(2023 = 183.11 + 10\)
Trong 1 chu kì có 11 lần và lần thứ 10 ở \(k = 12 \Rightarrow u = 0,2m = A/2\))
\( \Rightarrow \alpha = 183.2\pi + \frac{{3\pi }}{2} + \frac{\pi }{3} = \frac{{2207\pi }}{6} \Rightarrow t = \frac{{2207T}}{{12}} = \frac{{2207.3}}{{12}} = 551,75s\)
Chọn A
