(2023) Đề thi thử Vật Lí THPT Trần Phú có đáp án
-
912 lượt thi
-
40 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Những đại lượng đồng thời cực đại trong quá trình một vật dao động điều hòa dao động là
 Xem đáp án
Xem đáp án
Vì\(\)\({W_\~n } = \frac{1}{2}.m.{v^2}\)nên chọn đáp án \(C\)
Câu 2:
Vận tốc truyền sóng phụ thuộc vào
 Xem đáp án
Xem đáp án
Sóng cơ học là sóng vật chất, nên vận tốc truyền sóng cơ học phụ thuộc vào bản chất của môi trường truyền sóng, môi trường có mật độ phần tử vật chất dày thì truyền đi càng nhanh.
đáp án \(C\)
Câu 3:
Chọn câu đúng: Chu kì dao động điều hòa của con lắc lò xo phụ thuộc vào
 Xem đáp án
Xem đáp án
Vì \(T = 2\pi .\sqrt {\frac{m}{k}} \) Đáp án B
Câu 4:
Cho hai dao động điều hòa \({x_1} = {A_1}\cos \left( {\omega t + {\varphi _1}} \right);{x_2} = {A_2}\cos \left( {\omega t + {\varphi _2}} \right)\). Biên độ dao động tổng hợp của chúng đạt cực đại khi
 Xem đáp án
Xem đáp án
\(\begin{array}{l}Ta\,\,co\`u \,:\,\,{A^2} = A_1^2\, + \,\,A_2^2\, + \,2.{A_1}.{A_2}.\cos ({\varphi _2} - {\varphi _1})\\Muo\'a n\,\,{A_{\max }} \Leftrightarrow \cos ({\varphi _2} - {\varphi _1}) = 1 \Rightarrow {\varphi _2} - {\varphi _1} = 2.k.\pi \end{array}\)
Đáp án B
Câu 5:
Cho con lắc đơn chiều dài \(l\) dao động điều hoà với chu kỳ T. Tại nơi đó, nếu tăng chiều dài con lắc gấp 16 lần và tăng khối lượng vật treo gấp 4 lần thì chu kỳ con lắc
 Xem đáp án
Xem đáp án
ADCT: \[\begin{array}{l}{T_1} = 2\pi .\sqrt {\frac{{{l_1}}}{g}} \\{T_2} = 2\pi .\sqrt {\frac{{{l_2}}}{g}} \,\,v\^o \`u i\,\,{l_2} = \,16.{l_1}\end{array}\]nên \(\frac{{{T_1}}}{{{T_2}}} = \sqrt {\frac{{{l_1}}}{{{l_2}}} = \frac{1}{{16}}} = \frac{1}{4} \Rightarrow {T_2} = 4.{T_1}\). Chọn Đáp án B
Câu 6:
Một vật dao động điều hòa theo phương trình \(x = A\cos (\omega t + \varphi )(cm)\), đại lượng \(\omega t + \varphi \) gọi là
 Xem đáp án
Xem đáp án
Đáp án B. đại lượng \(\omega t + \varphi \)là pha dao động vào lúc t
Câu 7:
Một chất điểm dao động điều hoà trên trục \(Ox\). Khi đi từ vị trí biên về vị trí cân bằng thì
 Xem đáp án
Xem đáp án
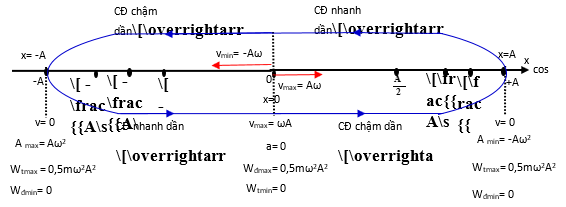
Khi đi từ vị trí biên về vị trí cân bằng thì vật CĐ nhanh dần độ lớn gia tốc của vật giảm.
Đáp án A
Câu 8:
Tìm ý sai khi nói về dao động điều hòa của con lắc đơn.
 Xem đáp án
Xem đáp án
A. Dựa vào định nghĩa con lắc đơn dao động điều hòaà A đúng.
B. Tốc độ tăng nên chuyển động nhanh dần
C. Tại vị trí biên, động năng bằng không nên thế năng bằng cơ năng.
D. \(T = 2.\pi .\sqrt {\frac{l}{g}} \Rightarrow T \sim \sqrt l \)
Đáp án D
Câu 9:
 Xem đáp án
Xem đáp án
\(T = \frac{1}{f} = \frac{1}{5} = 0,2\,s\)
\(\frac{T}{{{T^/}}} = \sqrt {\frac{m}{{{m^/}}}} \Rightarrow \frac{{0,2}}{{0,1}} = \sqrt {\frac{m}{{m - 0,15}}} \Rightarrow m = 0,2kg\) Đáp án D.
Câu 10:
Khi nói về sóng cơ, phát biểu sai là
 Xem đáp án
Xem đáp án
A. Dựa vào định nghĩa sóng dọc và sóng ngangàA đúng
B. Sóng cơ là sóng vật chấtàB đúng
C. Dựa vào định nghĩa sóng dọc và sóng ngangàC đúng
D. Khi sóng truyền đi, các phần tử vật chất chỉ dao động quanh vị trí cân bằng, chỉ có pha của dao động và năng lượng của dao động được truyền điàD sai
Đáp án D
Câu 11:
Một con lắc lò xo có độ cứng \(k = 40\;N/m\) đang dao động điều hòa. Lúc động năng \(20\;mJ\) thì thế năng bằng \(12\;mJ\). Mốc thế năng được chọn ở vị trí cân bằng. Biên độ dao động của vật bằng
 Xem đáp án
Xem đáp án
Định luật bảo toàn năng lượng:
\(\begin{array}{l}W = {W_\~n }\, + \,{W_t} = \,20 + 12 = 32mJ = {32.10^{ - 3}}J\\Ma{\o}\,\,W = \frac{1}{2}.K.{A^2} \Rightarrow {32.10^{ - 3}} = \frac{1}{2}.40.{A^2} \Rightarrow A = 0,04(m) = 4(cm)\end{array}\)
Đáp án C
Câu 12:
Biên độ dao động cưỡng bức càng lớn khi
 Xem đáp án
Xem đáp án
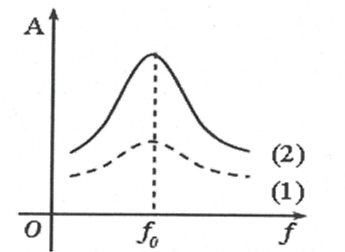
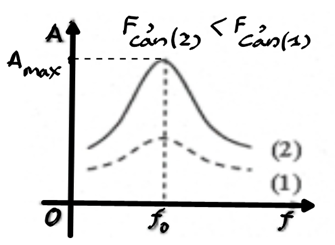
Hiện tượng cộng hưởng sẽ nhọn nếu: hệ số masát nhỏ, và sẽ tù nếu : hế số ma sát lớn
Đáp án A
Câu 13:
Khi một sóng cơ truyền từ không khí vào nước thì
 Xem đáp án
Xem đáp án
Áp dụng công thức: \(\lambda = \frac{v}{f}\)
Sóng cơ: Truyền từ môi trường này sang môi trương khác thì tần số không thay đổi, nên bước sóng và tốc độ truyền sóng thay đổi tỉ lệ thuận với nhau
\(\begin{array}{l}{v_{kh\'i }} < {v_{lo\^u ng}} < {v_{ra\'e n}}\\{\lambda _{kh\'i }} < {\lambda _{lo\^u ng}} < {\lambda _{ra\'e n}}\end{array}\)nên Đáp án B
Sóng điện từ: Truyền từ môi trường này sang môi trương khác thì tần số không thay đổi, nên bước sóng và tốc độ truyền sóng thay đổi tỉ lệ thuận với nhau
\(\begin{array}{l}{v_{kh\'i }} > {v_{lo\^u ng}} > {v_{ra\'e n}}\\{\lambda _{kh\'i }} > {\lambda _{lo\^u ng}} > {\lambda _{ra\'e n}}\end{array}\)
Câu 14:
Hai dao động điều hoà cùng phương cùng tần số \({x_1} = A\cos (\omega t + \pi /3)\) và \({x_2} = A\cos (\omega t - 2\pi /3)\) là hai dao động
 Xem đáp án
Xem đáp án
\(\left. \begin{array}{l}{\varphi _1} = \frac{\pi }{3}\\{\varphi _2} = - \frac{{2\pi }}{3}\end{array} \right\} \Rightarrow \Delta \varphi = {\varphi _2} - {\varphi _1} = - \pi \) nên đáp án A
Câu 15:
Một vật dao động điều hoà có phương trình dao động \(x = 2\sin (5\pi t + \pi /3)cm\). Vận tốc của vật ở thời điểm \(t = 2(\;s)\) là
 Xem đáp án
Xem đáp án
Cách 1:
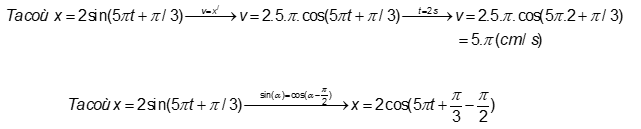
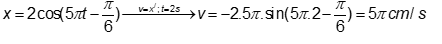
Đáp án B
Câu 16:
Cho hai dao động điều hòa cùng phương, cùng tần số, ngược pha, có biên độ lần lượt là \({A_1}\) và \({A_2}\). Biên độ dao động tổng hợp của hai dao động này là
 Xem đáp án
Xem đáp án
\(\begin{array}{l}Ta\,\,co\`u \,:\,\,{A^2} = A_1^2\, + \,\,A_2^2\, + \,2.{A_1}.{A_2}.\cos ({\varphi _2} - {\varphi _1})\\V\`i \,\,2\,\,dao\,\,\~n o\"a ng\,\,ng\"o \^o \"i c\,\,pha\,\,ne\^a n\,\,\Delta \varphi = {\varphi _2} - {\varphi _1} = (2k + 1)\pi \Rightarrow \cos ({\varphi _2} - {\varphi _1}) = - 1 \Rightarrow {A^2} = {({A_1} - {A_2})^2}\end{array}\)
Đáp án A
Câu 17:
Một con lắc lò xo gồm lò xo và vật nhỏ có khối lượng \(m\) đang dao động điều hòa theo phương nằm ngang. Khi vật có tốc độ \(v\) thì động năng của con lắc được tính bằng công thức nào sau đây?
 Xem đáp án
Xem đáp án
Đáp án B. động năng của con lắc \({W_d} = \frac{1}{2}m{v^2}\)
Câu 18:
 Xem đáp án
Xem đáp án
\(W = \frac{1}{2}K.{A^2}\) nên đáp án B
Lưu ý: Tránh suy luận theo cách sau
nên chọn đáp án D (sai) vì độ cứng của lò xo không phụ thuộc vào khối lượng vật nặng gắn vào lò xo đó.
Câu 19:
Đối với dao động điều hoà, chu kỳ dao động là khoảng thời gian ngắn nhất để một trạng thái của dao động lặp lại như cũ. Trạng thái cũ ở đây bao gồm những thông số nào?
 Xem đáp án
Xem đáp án
Trạng thái của một vật được đặc trưng bởi 2 thông số x, v theo đúng định nghĩa của dao động tuần hoàn (Trang 4 SGK Vật Lí 12) nên đáp án D
Câu 20:
Trong dao động điều hòa của con lắc lò xo, đại lượng không biến thiên điều hòa theo thời gian là
 Xem đáp án
Xem đáp án
\(\begin{array}{l}x(t) = A.\cos (\omega .t + \varphi )\\a(t) = - {\omega ^2}.x\\{F_{hp}}(t) = - k.x\\W = \frac{1}{2}.K.{A^2}\end{array}\)nên đáp án D
Câu 21:
Con lắc đơn dao động điều hòa tại nơi có \(g = 9,81\;m/{s^2}\), với chu kì \(T = 2\;s\). Chiều dài của con lắc là
 Xem đáp án
Xem đáp án
\(T = 2\pi .\sqrt {\frac{l}{g}} \Rightarrow l = \frac{{{T^2}.g}}{{4{\pi ^2}}} = \frac{{{2^2}.9,81}}{{4{\pi ^2}}} = 0,9939 \approx 0,994\,(m)\)
Góp ý: Nên sửa số liệu \(g = 9,810\,(\;m/{s^2})\) và T = 2,000 (s) để quy ước làm tròn 3 số sau dấu phẩy (4 chữ số có nghĩa). đáp án C
Câu 22:
Nguồn phát sóng \(S\) trên mặt nước tạo dao động với tần số \(f = 100\;Hz\) gây ra các sóng có biên độ \(A = 0,4\;cm\). Biết khoảng cách giữa 7 gợn lồi liên tiếp là \(3\;cm\). Vận tốc truyền sóng trên mặt nước là
 Xem đáp án
Xem đáp án
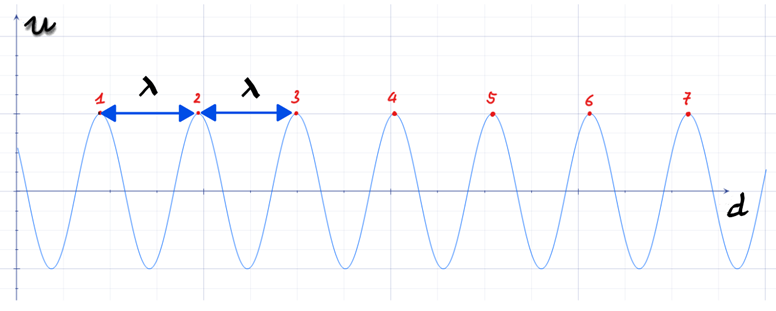
\(\begin{array}{l}6\lambda = 3 \Rightarrow \lambda = 0,5(cm)\\v = \lambda .f = 0,5.100 = 50(cm/s)\end{array}\)Chọn đáp án A
Câu 23:
Con lắc lò xo có độ cứng \(k = 10\;N/m\), khối lượng \({\rm{10}}\;g\) đang dao động điều hòa. Kéo con lắc khỏi vị trí cân bằng \({\rm{2}}\;cm\) rồi buông nhẹ. Gia tốc cực đại của vật là
 Xem đáp án
Xem đáp án
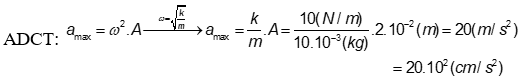
Chọn đáp án C
Câu 24:
Nguồn sóng có phương trình \({u_0} = 5\cos \left( {2\pi t + \frac{\pi }{6}} \right)(cm)\). Biết sóng lan truyền với bước sóng \(40\;cm\). Coi biên độ sóng không đổi. Phương trình dao động của sóng tại điểm \(M\) cách \(O\) một đoạn \(10\;cm\) nằm trên phương truyền sóng là:
 Xem đáp án
Xem đáp án
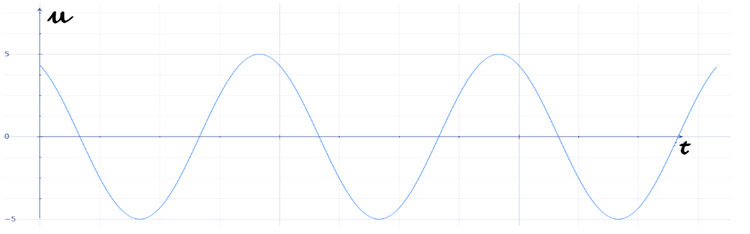
Ta có: \(\begin{array}{l}{u_M} = 5.\cos (2\pi .t + \frac{\pi }{6} - \frac{{2\pi .x}}{\lambda })\\\,\,\,\,\,\,\, = 5.\cos (2\pi .t + \frac{\pi }{6} - \frac{{2\pi .10\,cm}}{{40\,cm}}) = 5.\cos (2\pi .t - \frac{\pi }{3})\end{array}\)
Chọn đáp án C
Câu 25:
 Xem đáp án
Xem đáp án
\(T = 2\pi .\sqrt {\frac{l}{g}} \)
Chiều dài phụ thuộc vào nhiệt độ của môi trường (sự nở vì nhiệt).
Gia tốc trọng trường g phụ thuộc vào khoảng cách của con lắc với tâm của Trái Đấtàg phụ thuộc vào vĩ độ địa lý.
àChọn đáp án D
Câu 26:
Một con lắc đơn có độ dài \(l\), trong khoảng thời gian \(\Delta t\) nó thực hiện được \({\rm{6}}\) dao động. Người ta giảm bớt độ dài của nó đi \(28\;cm\), cũng trong thời gian \(\Delta t\) như trước nó thực hiện được 8 dao động. Chiều dài của con lắc ban đầu là
 Xem đáp án
Xem đáp án
\(\left. \begin{array}{l}T = \frac{{\Delta t}}{6}\\{T^/} = \frac{{\Delta t}}{8}\end{array} \right\}\frac{T}{{{T^/}}} = \frac{8}{6} = \frac{4}{3}\) mà \(\frac{T}{{{T^/}}} = \sqrt {\frac{l}{{{l^/}}}} \Rightarrow \sqrt {\frac{l}{{{l^/} = l - 28}}} = \frac{4}{3} \Rightarrow l = 64(cm)\)
Chọn đáp án B
Câu 27:
Phát biểu nào sau đây về dao động cưỡng bức là đúng
 Xem đáp án
Xem đáp án
A. Đúng định nghĩa của dao động cưỡng bức
B. Đây là trường hợp đặc biệt của dao động cưỡng bức, hiện tượng cộng hưởng.
C. Biên độ của dao động cưỡng bức phụ vào biên độ của ngoại lực tuần hoàn thuộc (chứ không phải bằng vì khác nhau về đơn vị đo, một bên là cm, một bên là Niuton).
D. Dao động cưỡng bức là dao dộng có tần số đúng bằng tần số của ngoại lực, ngoại lực này biến thiên tuần hoàn theo thời gian \(F = {F_0}.\cos (\omega t + \varphi )\), cho nên, tần số của ngoại lực luôn là đại lượng không phụ thuộc thời gian.
Đáp án A.
Câu 28:
Bộ phận giảm xóc ở bánh sau của xe gắn máy có sự ứng dụng của
 Xem đáp án
Xem đáp án
A. Dao động tắt dần: Bộ phận giảm xóc ở bánh sau của xe gắn máy
B. Dao động điều hòa: Con lắc lò xo, con lắc đơn khi bỏ qua lực ma sát
C. Dao động duy trì: Dao động của con lắc đồng hồ
D. Dao động tự do: Con lắc lò xo, con lắc đơn khi bỏ qua lực ma sát
đáp án A
Câu 29:
Một con lắc đơn dài \({\rm{44}}\;cm\) được treo vào trần của một toa xe lửa. Con lắc bị kích động mỗi khi bánh của toa xe gặp chỗ nối nhau của đường ray. Biết chiều dài của mỗi đoạn đường ray là \({\rm{12}},5\;m\). Cho \(g = {\pi ^2}\;m/{s^2}\). Hỏi tàu chạy thẳng đều với tốc độ bằng bao nhiêu thì biên độ dao động của con lắc sẽ lớn nhất
 Xem đáp án
Xem đáp án
Mỗi khi bánh xe gặp chỗ nối nhau của đường ray thì con lắc bị tác động một lực sinh ra do sự va chạm giữa bánh xe với chỗ nối. Dao động của con lắc đơn lúc này là dao động cưỡng bức.
Vì xe chuyển động thẳng đều nên thời gian giữa 2 lần liên tiếp con lắc bị tác động lực là: \(t = \frac{{12,5}}{v}\)
Thời gian này chính là chu kì của ngoại lực tuần hoàn.
Biên độ dao động của con lắc sẽ lớn nhất khi xảy ra cộng hưởng: \({T_{rie\^a ng}} = {T_{ngoa\"i i\,\,l\"o \"i c}}\)
Chọn đáp án A
Câu 30:
Con lắc đơn có chiều dài \(l\), đặt ở nơi có \(g = {\pi ^2}\;m/{s^2}\). Con lắc này dao động dưới tác dụng của ngoại lực \(F = 40\cos (\pi t)N\) thì con lắc dao động có biên độ cực đại. Tính chiều dài con lắc
 Xem đáp án
Xem đáp án
Biên độ dao động của con lắc sẽ lớn nhất khi xảy ra cộng hưởng:
\({\omega _{rie\^a ng}} = {\omega _{ngoa\"i i\,\,l\"o \"i c}} \Rightarrow \sqrt {\frac{{g = {\pi ^2}(m/{s^2})}}{l}} = \pi \Rightarrow l = 1(m)\)
Chọn đáp án D
Câu 31:
Một vật thực hiện đồng thời hai dao động điều hoà cùng phương, cùng tần số có biên độ lần lượt là 8 cm và 2 cm. Biên độ dao động tổng hợp có thể là
 Xem đáp án
Xem đáp án
\(\begin{array}{l}\left| {{A_1} - {A_2}} \right| \le A \le {A_1} + {A_2}\\ \Rightarrow \left| {8 - 2} \right| \le A \le 8 + 2\\ \Rightarrow 6 \le A \le 10\end{array}\)
Chọn đáp án B
Câu 32:
Một vật có khối lượng \({\rm{10}}\;g\) đang dao động điều hòa với biên độ \({\rm{5}}\;cm\) và tần số góc là \({\rm{10}}rad/s\). Lực kéo về cực đại tác dụng lên vật là
 Xem đáp án
Xem đáp án
Chọn đáp án A
Câu 33:
Chuyển động của một vật là tổng hợp của hai dao động điều hòa cùng phương. Hai dao động này có phương trình lần lượt là \({x_1} = 6{\rm{cos}}\left( {10t + \frac{\pi }{2}} \right)\)cm và \({x_2} = 8{\rm{cos}}\left( {10t + \pi } \right)\)cm. Độ lớn vận tốc của vật ở vị trí cân bằng là
 Xem đáp án
Xem đáp án
Sử dụng máy tính tìm dao động tổng hợp của 2 dao động thành phần:
\(\begin{array}{l}x = {x_1} + {x_2}\\ \Rightarrow A\angle \varphi = {A_1}\angle {\varphi _1} + {A_2}\angle {\varphi _2}\\ \Rightarrow A\angle \varphi = 6\angle \frac{\pi }{2} + 8\angle \pi = 10\angle 2,5\end{array}\)
Phương trình dao động tổng hợp: \(\begin{array}{l}x = 10.\cos (10t + 2,5)\\ \Rightarrow {v_{\max }} = \omega .A = 10.10 = 100(cm/s)\end{array}\)
Chọn đáp án B
Câu 34:
Hai vật A và B dao động điều hòa cùng tần số. Hình bên là đồ thị biểu diễn sự phụ thuộc của li độ x1 của A và li độ x2 của B theo thời gian t. Hai dao động của A và B lệch pha nhau:
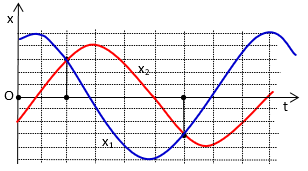
 Xem đáp án
Xem đáp án
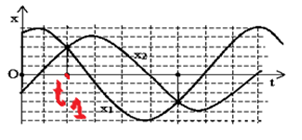
Xét dao động \({x_1}\): Pha dao động tại thời điểm \({t_1}\):
\({\mathop{\rm Cos}\nolimits} (\omega .{t_1} + {\varphi _1}) = \frac{{{x_1} = 3\,o\^a }}{{A = 5\,o\^a }} \Rightarrow \omega .{t_1} + {\varphi _1} = \pm {\cos ^{ - 1}}(\frac{3}{5}) + k2\pi \)
Tại thời điểm \({t_1}\): Vật 1 đang chuyển động về vị trí cân bằng theo chiều âm, nên pha dao động phải dương. Do đó, \(\omega .{t_1} + {\varphi _1} = {\cos ^{ - 1}}(\frac{3}{5}) + k2\pi \)
Xét dao động \({x_2}\): Pha dao động tại thời điểm \({t_1}\):
\({\mathop{\rm Cos}\nolimits} (\omega .{t_1} + {\varphi _2}) = \frac{{{x_1} = 3\,o\^a }}{{A = 4\,o\^a }} \Rightarrow \omega .{t_1} + {\varphi _2} = \pm {\cos ^{ - 1}}(\frac{3}{4}) + k2\pi \)
Tại thời điểm \({t_1}\): Vật 2 đang chuyển động đến vị trí biên dương nên pha dao động phải âm. Do đó, \(\omega .{t_1} + {\varphi _2} = - {\cos ^{ - 1}}(\frac{3}{4}) + k2\pi \)
Độ lệch pha giữa hai dao động là:
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = - {\cos ^{ - 1}}(\frac{3}{4}) - {\cos ^{ - 1}}(\frac{3}{5}) = - \,1,65(rad)\)
Chọn đáp án D.
Giải 2:
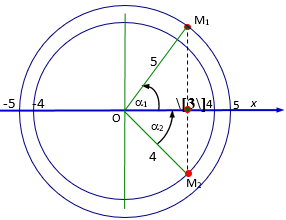
Từ đồ thị, ta có biên độ:
A1=5 ô ; A2 = 4 ô
Xét lúc 2 dao động cùng có li độ:
x1 =x2 =3 ô.
Dùng vòng tròn lượng giác:
Độ lệch pha của 2 dao động:
\[\begin{array}{l}\Delta \varphi = {\alpha _1} + {\alpha _2} = {\cos ^{ - 1}}(\frac{3}{5}) + {\cos ^{ - 1}}(\frac{3}{4})\\ = 0.927 + 0,7227 = 1,649\;rad\end{array}\]
Câu 35:
Nguồn sóng đặt tại O dao động với tần số 10 Hz. Điểm M nằm cách O đoạn 20 cm. Biết tốc độ truyền sóng là 40 cm/s. Giữa O và M có bao nhiêu điểm dao động ngược pha với nguồn?
 Xem đáp án
Xem đáp án
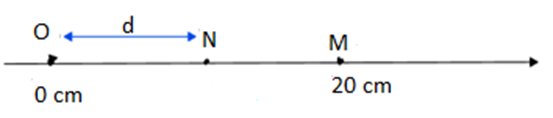 Gọi N là điểm nằm giữa O và M, thỏa mãn điều kiện dao động ngược pha với nguồn (d = ON)
Gọi N là điểm nằm giữa O và M, thỏa mãn điều kiện dao động ngược pha với nguồn (d = ON)
Vì N là điểm nằm giữa O và M nên thỏa mãn điều kiện sao: \(\begin{array}{l}0 \le \,d = (2k + 1).2 \le 20\\ \Rightarrow \frac{{ - 1}}{2} \le \,k \le 4,5 \Rightarrow k = 0,\,1,\,2,\,3,\,4\end{array}\)
Chọn đáp án B
Câu 36:
Hai dao động điều hòa \({x_1} = 3\cos \left( {4\pi t - \frac{\pi }{3}} \right)(cm;s)\) và \({x_2} = 4\cos (4\pi t + \varphi )(cm;s)\). Biên độ dao động tổng hợp \(A = 5\;cm\) khi:
 Xem đáp án
Xem đáp án
Cách 1: Dùng máy tính tổng hợp dao động bằng số phức, với \(\varphi \)là 1 trong 4 đáp án:
\(\begin{array}{l}x = {x_1} + {x_2}\\ \Rightarrow 5\angle \beta = 3\angle - \frac{\pi }{3} + 4\angle \varphi \end{array}\)
Thay \(\varphi = \frac{\pi }{6}\)vào ta có: \(5\angle \beta = 3\angle - \frac{\pi }{3} + 4\angle \frac{\pi }{6}\)thỏa mãn biên độ tổng hợp bằng 5(cm) nên chọn đáp án A
Cách 2:
\[{5^2} = {3^2} + {4^2} + 2.3.4.\cos (\varphi - ( - \frac{\pi }{3}))\]. Thay các giá trị của 4 đáp án vào, thấy rằng đáp án A thỏa mãn.
Câu 37:
Con lắc đơn có chiều dài \(\ell = 1\;m\), \(g = 10\;m/{s^2} = {\pi ^2}\). Con lắc dao động với biên độ \({\alpha _0} = {9^0}\).
Tốc độ của vật khi qua vị trí cân bằng là: Xem đáp án
Xem đáp án
ADCT: \(v = \sqrt {2\lg .(\cos (\alpha ) - \cos ({\alpha _0})} \)
Vật ở VTCB thì \(\alpha = {0^0} \Rightarrow v = \sqrt {2.1.10.(\cos (0) - \cos ({9^0}))} = 0,496 \approx 0,5(m/s)\)
Chọn đáp án D
Câu 38:
Một con lắc lò xo dao động điều hòa theo phương ngang với biên độ \({\rm{6}}\;cm\). Nếu chọn mốc thế năng tại vị trí cân bằng thì khi lực kéo về có độ lớn \({\rm{3}}\;N\) con lắc có thế năng bằng \({\rm{45}}\;mJ\) và có động năng bằng
 Xem đáp án
Xem đáp án
ADCT: \(\begin{array}{l}\left. \begin{array}{l}{F_{kv}} = - Kx \Rightarrow \left| {{F_{kv}}} \right| = K.\left| x \right| = 3(N) \Rightarrow \left| x \right| = \frac{3}{K}\\{W_t} = \frac{1}{2}.K.{x^2} = {45.10^{ - 3}}(J)\end{array} \right\} \Rightarrow \frac{1}{2}.K.{(\frac{3}{K})^2} = {45.10^{ - 3}} \Rightarrow K = 100(N/m)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| x \right| = 0,03(m)\end{array}\)
Bảo toàn năng lượng:
\(W = {W_\~n } + {W_t} \Rightarrow {W_\~n } = W - {W_t} = \frac{1}{2}.K({A^2} - {x^2}) = 0,135(J) = 135(mJ)\)
Chọn đáp án D
Câu 39:
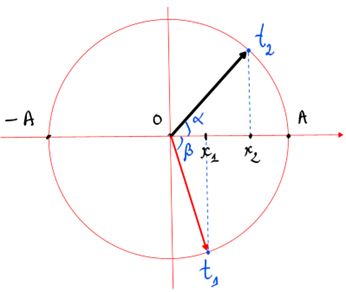
Một chất điểm dao động điều hòa trên trục \(Ox\) với chu kỳ 1,2 s. Tại thời điểm \({t_1}\) chất điểm có ly độ \({x_1} = 2\sqrt 5 \;cm\) và tại thời điểm \({t_2} = {t_1} + 1,5(s)\) chất điểm có ly độ \({x_2} = 4\sqrt 5 \;cm\). Chiều dài quỹ đạo là
 Xem đáp án
Xem đáp án
Ta có:
Suy ra, vecto biểu diễn dao động \({x_1}\)vuông góc với vecto biểu diễn dao động \({x_2}\)nên ta luôn có biểu thức sau đây:
\({(\frac{{{x_1}}}{A})^2} + {(\frac{{{x_2}}}{A})^2} = 1 \Rightarrow x_1^2 + x_2^2 = {A^2} \Rightarrow A = 10(cm)\)
Suy ra, chiều dài quỹ đạo là: L=2.A=20(cm)
Chọn đáp án B
Lưu ý: Chứng minh biểu thức độc lập thời gian của 2 vecto vuông góc với nhau
Câu 40:
Một vật nhỏ dao động điều hòa theo một quỹ đạo thẳng dài 14 cm với chu kì 1 s. Từ thời điểm vật qua vị trí có li độ 3,5 cm theo chiều dương đến khi gia tốc của vật đạt giá trị cực tiểu lần thứ hai, vật có tốc độ trung bình là
 Xem đáp án
Xem đáp án
Công Thức: \(To\'a c\,\,\~n o\"a \,\,trung\,\,b\`i nh = \frac{{Qua\~o ng\,\,\~n \"o \^o {\o}ng\,\~n i\,\,\~n \"o \^o \"i c\,\,trong\,\,th\^o {\o}i\,\,gian\,\,t}}{{Th\^o {\o}i\,\,gian\,\,th\"o \"i c\,\,hie\"a n\,\,qua\~o ng\,\,\~n \"o \^o {\o}ng\,\,\~n o\`u }}\)
\(L = 2.A \Rightarrow A = \frac{L}{2} = 7(cm)\)
Gia tốc đạt giá trị cực tiểu tại vị trí biên dương ()
Sử dụng đường tròn lượng giác để giải:
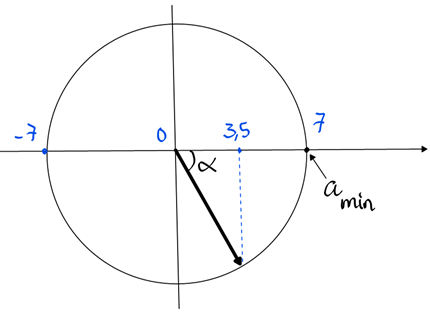
Quãng đường: \(S = \frac{A}{2} + 4.A = 3,5 + 4.7 = 31,5(cm)\)
Thời gian: \(t = {t_{\frac{A}{2} \to A}} + T = (\frac{T}{4} - \frac{T}{{12}}) + T = \frac{7}{6}(s)\)
Tốc độ trung bình: \({v_{tb}} = \frac{s}{t} = 27(cm/s)\)
Đáp án C.
