Bộ đề thi thử môn Toán THPT Quốc gia năm 2022 có lời giải (30 đề)
Đề thi thử môn Toán THPT Quốc gia năm 2022 có lời giải (Đề 12)
-
3717 lượt thi
-
50 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Đồ thị hàm số có tiệm cận ngang là:
 Xem đáp án
Xem đáp án
Phương pháp:
Đồ thị hàm số có TCN là
Cách giải:
Đồ thị hàm số có tiệm cận ngang là y = -3.
Chọn D.
Câu 2:
 Xem đáp án
Xem đáp án
Phương pháp:
- Xét phương trình hoành độ giao điểm.
- Tìm điều kiện để phương trình hoành độ giao điểm có 2 nghiệm phân biệt.
Cách giải:
TXĐ:
Xét phương trình hoành độ giao điểm
Để đường thẳng d cắt đồ thị (C) tại hai điểm phân biệt thì phương trình (*) có 2 nghiệm phân biệt khác
Chọn A.
Câu 3:
Hàm số nghịch biến trên khoảng nào dưới đây?
 Xem đáp án
Xem đáp án
Phương pháp:
- Tìm TXĐ.
- Sử dụng công thức tính đạo hàm
- Giải bất phương trình y' < 0 và suy ra khoảng nghịch biến của hàm số.
Cách giải:
Vì nên TXĐ của hàm số là D = .
Ta có
Xét
Vậy hàm số nghịch biến trên khoảng
Chọn B.
Câu 4:
Cho hàm số Phát biểu nào sau đây đúng?
 Xem đáp án
Xem đáp án
Phương pháp:
Hàm phân thức bậc nhất trên bậc nhất đơn điệu trên từng khoảng xác định của nó.
Cách giải:
TXĐ: Ta có
Vậy hàm số nghịch biến trên
Chọn A.
Câu 5:
Trong không gian tọa độ Oxyz cho ba điểm và C(2; 1; -1). Phương trình mặt phẳng (ABC) là:
 Xem đáp án
Xem đáp án
Phương pháp:
- Mặt phẳng (ABC) nhận làm 1 VTPT.
- Trong không gian Oxyz, mặt phẳng đi qua điểm và nhận làm vectơ pháp tuyến có phương trình là:
Cách giải:
Ta có
có 1 VTPT là
Phương trình mặt phẳng (ABC) là:
Chọn B.
Câu 6:
Số phức liên hợp của số phức z = 4 + 7i là:
 Xem đáp án
Xem đáp án
Phương pháp:
Số phức z = a + bi có số phức liên hợp là
Cách giải:
Chọn B.
Câu 7:
Cho hàm số f(x) liên tục trên đoạn [0; 2]. Biết và Tính
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng tính chất tích phân:
Cách giải:
Chọn B.
Câu 8:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng công thức tính đạo hàm:
Cách giải:
Chọn D.
Câu 9:
Cho F(x) là một nguyên hàm của hàm số trên khoảng Tìm F(x) biết F(1) = 5.
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng công thức tính nguyên hàm mở rộng:
Cách giải:
Vì
Mà
Vậy
Chọn D.
Câu 10:
Biết phương trình có 2 nghiệm Tính
 Xem đáp án
Xem đáp án
Phương pháp:
- Đặt ẩn phụ
- Áp dụng định lí Vi-ét.
Cách giải:
Đặt phương trình trở thành
Giả sử phương trình có 2 nghiệm phân biệt
Chọn B.
Câu 11:
 Xem đáp án
Xem đáp án
Phương pháp:
Tính tích phân bằng phương pháp đổi biến số, đặt
Cách giải:
Đặt
Đổi cận:
Chọn B.
Câu 12:
Cho biết với và là phân số tối giản. Tính a + b.
 Xem đáp án
Xem đáp án
Phương pháp:
Tính tích phân bằng phương pháp đưa biến vào vi phân.
Cách giải:
Ta có
Chọn C.
Câu 13:
Trong không gian tọa độ Oxyz, cho ba điểm và C(0; -11; 2) Viết phương trình đường thẳng d đi qua A và song song với BC.
 Xem đáp án
Xem đáp án
Phương pháp:
- Đường thẳng d//BC nhận làm 1 VTCP.
- Trong không gian Oxyz, phương trình của đường thẳng d đi qua điểm và có vectơ chỉ phương là:
Cách giải:
Đường thẳng d//BC nhận làm 1 VTCP.
Phương trình đường thẳng d là:
Chọn A.
Câu 14:
Cho số phức z thỏa mãn Tính mô-đun của z.
 Xem đáp án
Xem đáp án
Phương pháp:
- Thực hiện các phép tính tìm số phức z
- Số phức
Cách giải:
Ta có:
Vậy
Chọn C.
Câu 15:
Cho hàm số y = f(x) có bảng biến thiên như sau:
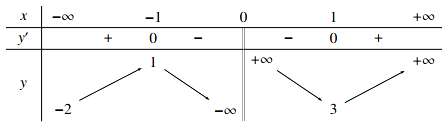
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = f(x) là:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng khái niệm đường tiệm cận của đồ thị hàm số: Cho hàm số y = f(x).
- Đường thẳng là TCN của đồ thị hàm số nếu thỏa mãn một trong các điều kiện sau: hoặc
- Đường thẳng là TCĐ của đồ thị hàm số nếu thỏa mãn một trong các điều kiện sau: hoặc hoặc hoặc .
Cách giải:
Dựa vào BBT ta thấy:
là TCN của đồ thị hàm số.
là TCĐ của đồ thị hàm số.
Vậy đồ thị hàm số y = f(x) có tổng 2 đường tiệm cận.
Chọn D.
Câu 16:
Tìm tất cả các giá trị của tham số m để hàm số có ba điểm cực trị.
 Xem đáp án
Xem đáp án
Phương pháp:
Hàm số bậc bốn trùng phương có 3 điểm cực trị khi ab < 0.
Cách giải:
Hàm số đã cho có 3 điểm cực trị khi
Chọn B.
Câu 17:
Tập xác định của hàm số là:
 Xem đáp án
Xem đáp án
Phương pháp:
Hàm số xác định khi và chỉ khi f(x) xác định và f(x) > 0
Cách giải:
Hàm số xác định khi
Chọn D.
Câu 18:
Cho hình chóp S.ABC có và Thể tích khối chóp S.ABC bằng:
 Xem đáp án
Xem đáp án
Phương pháp:
- Tính
- Tính thể tích
Cách giải:
Ta có:
Vậy
Chọn B.
Câu 19:
Cho biết với Tính
 Xem đáp án
Xem đáp án
Phương pháp:
Tính tích phân bằng phương pháp tích phân từng phần.
Cách giải:
Đặt
Chọn B.
Câu 20:
Cho hình nón có bán kính đáy r = 3 và độ dài đường cao h = 4. Tính diện tích xung quanh của hình nón đó.
 Xem đáp án
Xem đáp án
Phương pháp:
- Tính độ dài đường sinh
- Diện tích xung quanh của hình nón có bán kính đáy r và độ dài đường sinh l là
Cách giải:
Độ dài đường sinh
Diện tích xung quanh của hình nón
Chọn D.
Câu 21:
 Xem đáp án
Xem đáp án
Phương pháp:
- Khối cầu ngoại tiếp hình lập phương cạnh a có đường kính bằng đường chéo của hình lập phương.
- Thể tích khối cầu bán kính R là
Cách giải:
Khối cầu ngoại tiếp hình lập phương cạnh a có đường kính bằng đường chéo của hình lập phương bằng nên có bán kính
Vậy thể tích khối cầu là
Chọn B.
Câu 22:
Trong mặt phẳng tọa độ Oxy cho hình phẳng (H) được giới hạn bởi các đường y = sin, y = 0, x = 0 và Quay hình phẳng (H) quanh trục Ox ta được một vật thể tròn xoay có thể tích bằng:
 Xem đáp án
Xem đáp án
Phương pháp:
Thể tích khối tròn xoay tạo thành khi quanh hình phẳng giới hạn bởi các đường , x = b, xung quanh trục Ox là:
Cách giải:
Thể tích cần tính:
Chọn C.
Câu 23:
Cho hàm số y = f(x) có đạo hàm Hàm số y = f(x) có bao nhiêu điểm cực trị?
 Xem đáp án
Xem đáp án
Phương pháp:
Xác định số điểm cực trị của hàm số = số nghiệm bội lẻ của phương trình f'(x) = 0.
Cách giải:
Ta có
Vậy hàm số f(x) có 3 điểm cực trị.
Chọn B.
Câu 24:
Trong không gian tọa độ Oxyz, cho mặt phẳng và điểm I(1; -1; 1). Viết phương trình mặt cầu tâm ![]() I và tiếp xúc với mặt phẳng (P)
I và tiếp xúc với mặt phẳng (P)
 Xem đáp án
Xem đáp án
Phương pháp:
- Mặt cầu tâm I và tiếp xúc với mặt phẳng (P) có bán kính
- Khoảng cách từ điểm đến mặt phẳng là
- Mặt cầu tâm I(a; b; c), bán kính R có phương trình
Cách giải:
Bán kính mặt cầu là
Vậy phương trình mặt cầu tâm I và tiếp xúc với mặt phẳng (P) là:
Chọn A.
Câu 25:
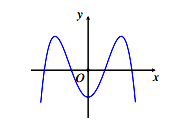
 Xem đáp án
Xem đáp án
Phương pháp:
- Dựa vào nhánh cuối cùng suy ra dấu của hệ số ![]()
- Dựa vào giao điểm của đồ thị với trục tung suy ra dấu của hệ số ![]()
- Hệ vào số điểm cực trị suy ra dấu của hệ số ![]()
Cách giải:
Đồ thị có nhánh cuối cùng đi xuống
Đồ thị cắt trục tung tại điểm nằm dưới trục hoành nên c < 0.
Đồ thị có 3 điểm cực trị Mà
Vậy
Chọn D.
Câu 26:
Cho hàm số y = f(x) liên tục trên và có bảng biến thiên như sau:
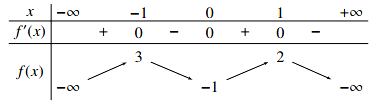
Số nghiệm của phương trình f(x) = 2 là:
 Xem đáp án
Xem đáp án
Phương pháp:
Số nghiệm của phương trình f(x) = m là số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = m song song với trục hoành.
Cách giải:
Đường thẳng y = 2 cắt đồ thị hàm số y = f(x) tại 3 điểm phân biệt nên phương trình f(x) = 2 có 3 nghiệm phân biệt.
Chọn C.
Câu 27:
Trong không gian Oxyz cho đường thẳng Vectơ nào sau đây là một vectơ chỉ phương của
 Xem đáp án
Xem đáp án
Phương pháp:
- Đưa phương trình đường thẳng về dạng
- Đường thẳng có 1 VTCP là
Cách giải:
có 1 VTCP là
Chọn B.
Câu 28:
Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số trên đoạn [1; 2]. Tính m + M.
 Xem đáp án
Xem đáp án
Phương pháp:
- Tính y' xác định các nghiệm của phương trình y' = 0.
- Tính
- KL: .
Cách giải:
Ta có
Mà
Vậy m + M = 1 + 4 = 5.
Chọn D.
Câu 30:
Trong mặt phẳng tọa độ Oxy, cho hình phẳng (H) được giới hạn bởi đồ thị hàm số và hai trục tọa độ Ox, Oy. Tính diện tích S của hình phẳng (H).
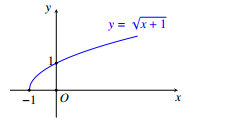
 Xem đáp án
Xem đáp án
Phương pháp:
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), y = g(x), đường thẳng x = a, x = b là
Cách giải:
Ta có:
Chọn D.
Câu 31:
Số nghiệm của phương trình là:
 Xem đáp án
Xem đáp án
Phương pháp:
Đặt ẩn phụ
Cách giải:
Đặt phương trình trở thành
Với
Vậy phương trình đã cho có 1 nghiệm.
Chọn C.
Câu 32:
Cho tứ diện ABCD. Gọi M, N, P lần lượt là trung điểm các cạnh AB, AC, AD và O là trọng tâm tam giác BCD. Tính tỉ số thể tích
 Xem đáp án
Xem đáp án
Phương pháp:
So sánh chiều cao và diện tích đáy của hai khối chóp.
Cách giải:
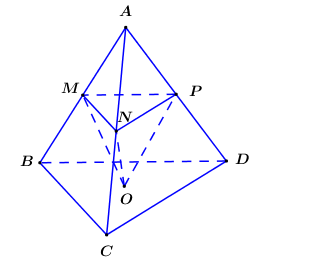
Vì theo tỉ số nên
Ta có
Lại có .
Vậy
Chọn B.
Câu 33:
Cho hàm số (m là tham số). Tìm m để hàm số có hai điểm cực trị.
 Xem đáp án
Xem đáp án
Phương pháp:
Tìm điều kiện để phương trình y' = 0 có 2 nghiệm phân biệt.
Cách giải:
Ta có
Để hàm số có hai điểm cực trị thì phương trình phải có 2 nghiệm phân biệt.
Chọn D.
Câu 34:
Cho lăng trụ đều ABC.A'B'C' có tất cả các cạnh đều bằng a. Thể tích khối lăng trụ ABC.A'B'C' là:
 Xem đáp án
Xem đáp án
Phương pháp:
Thể tích khối lăng trụ
Cách giải:
Thể tích khối lăng trụ
Chọn A.
Câu 35:
Cho hàm số Tìm m để
 Xem đáp án
Xem đáp án
Phương pháp:
Hàm phân thức bậc nhất trên bậc nhất đơn điệu trên từng khoảng xác định nên đạt GTNN và GTLN trên 1 đoạn xác định tại 2 điểm đầu mút.
Cách giải:
Hàm số đã cho xác định trên [0; 2], do đó nó đơn điệu trên [0; 2].
Chọn D.
Câu 36:
 Xem đáp án
Xem đáp án
Phương pháp:
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), y = g(x), đường thẳng x = a, x = b là
Cách giải:
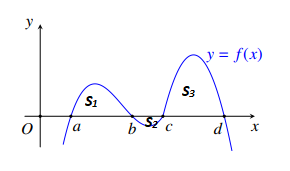
Ta có:
Ta có nên loại đáp án A và D.
Dễ thấy
Vậy
Chọn B.
Câu 37:
Tìm tất cả các giá trị của tham số m để phương trình có hai nghiệm trái dấu.
 Xem đáp án
Xem đáp án
Phương pháp:
- Đặt Đưa về phương trình bậc hai ẩn t
- Để phương trình ban đầu có 2 nghiệm trái dấu thì phương trình bậc hai ẩn t có 2 nghiệm phân biệt thỏa mãn
- Áp dụng định lí Vi-ét.
Cách giải:
Đặt phương trình trở thành
Giả sử phương trình ban đầu có 2 nghiệm phân biệt trái dấu
Phương trình (*) có 2 nghiệm phân phân biệt thỏa mãn
Chọn A.
Câu 38:
Cho f(x) và g(x) là hai hàm số có đạo hàm liên tục trên thỏa mãn và Tính
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng quy tắc tính đạo hàm một tích: .
Cách giải:
Ta có:
Câu 39:
Một khu rừng có trữ lượng gỗ là mét khối. Biết tốc độ sinh trưởng của các cây trong khu rừng đó là 4% một năm. Nếu hàng năm không khai thác thì sau 6 năm khu rừng đó có bao nhiêu mét khối gỗ?
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng công thức lãi kép.
Cách giải:
Nếu hàng năm không khai thác thì sau 6 năm khu rừng đó có: (mét khối).
Chọn D.
Câu 40:
 Xem đáp án
Xem đáp án
Phương pháp:
- Tham số hóa tọa độ điểm
- Cho tìm t và suy ra tọa độ điểm M.
- Tính
Cách giải:
Gọi
Vì
Chọn A.
Câu 41:
Trong không gian tọa độ Oxyz, cho hai mặt phẳng và Viết phương trình mặt phẳng (R) đi qua điểm A(-1; 0; 3) và chứa giao tuyến của (P) và (Q).
 Xem đáp án
Xem đáp án
Phương pháp:
- Xét hệ và suy ra phương trình đường thẳng giao tuyến của (P), (Q).
- Xác định là VTCP của đường thẳng giao tuyến.
- Lấy M thuộc giao tuyến (bất kì). Tính
- (R) có 1 VTPT là
- Trong không gian Oxyz, mặt phẳng đi qua điểm và nhận làm vectơ pháp tuyến có phương trình là:
Cách giải:
Gọi Phương trình đường thẳng
Cho z = t ta có
có 1 VTCP là và đi qua điểm
Ta có
Gọi là 1 VTCP của mặt phẳng (R). Ta có
Vậy phương trình mặt phẳng (R) là:
Chọn C.
Câu 42:
Trong không gian tọa độ Oxyz, cho đường thẳng và điểm A(1; 3; -1). Viết phương trình đường thẳng d đi qua điểm A cắt và vuông góc với đường thẳng .
 Xem đáp án
Xem đáp án
Phương pháp:
- Gọi tham số hóa tọa độ điểm
- Giải tìm t.
- Đường thẳng d đi qua A và có 1 VTCP là Viết phương trình đường thẳng d.
Cách giải:
Gọi
Đường thẳng có 1 VTCP là
Vì
là 1 VTCP của đường thẳng d.
Vậy phương trình đường thẳng d là:
Chọn C.
Câu 43:
Trong không gian tọa độ Oxyz, cho điểm M(2; -3; 1). Gọi A, B, C lần lượt là hình chiếu vuông góc của M trên các trục Ox, Oy, Oz. Viết phương trình mặt phẳng (ABC).
 Xem đáp án
Xem đáp án
Phương pháp:
- Hình chiếu của M(a; b; c) trên các trục Ox, Oy, Oz là
- Phương trình mặt phẳng đi qua 3 điểm là
Cách giải:
Hình chiếu của M(2; -3; 1) trên các trục Ox, Oy, Oz là
Phương trình mặt phẳng đi qua 3 điểm là
Chọn A.
Câu 44:
Cho hàm số f(x) liên tục trên thỏa mãn Tính
 Xem đáp án
Xem đáp án
Phương pháp:
- Lấy tích phân hai vế.
- Sử dụng phương pháp tính tích phân bằng phương pháp đổi biến số.
Cách giải:
Lấy tích phân từ 0 đến 1 hai vế của phương trình ta có:
Xét
Đặt
Đổi cận
Thay vào (*) ta có
Chọn B.
Câu 45:
Trong không gian tọa độ Oxyz, cho mặt cầu (S) có phương trình là (trong đó m là tham số).
Tìm tất cả các giá trị của m để mặt cầu (S) có diện tích bằng
 Xem đáp án
Xem đáp án
Phương pháp:
- Diện tích mặt cầu bán kính R là từ đó tính diện tích mặt cầu.
- Mặt cầu có bán kính
Cách giải:
Gọi R là bán kính mặt cầu ta có
Chọn A.
Câu 46:
Có bao nhiêu số nguyên m thỏa mãn
 Xem đáp án
Xem đáp án
Phương pháp:
Cô lập m đưa bất phương trình về dạng
Cách giải:
Ta có:
Đặt ta có
Sử dụng MTCT ta vẽ được BBT hàm số g(x) như sau:
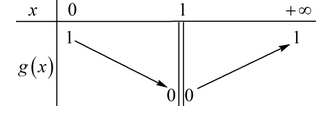
có nghiệm khi và chỉ khi
Vậy có vô số giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Chọn C.
Câu 47:
Trong không gian tọa độ Oxyz, cho ba điểm và mặt phẳng Khi điểm M thay đổi trên mặt phẳng (P), hãy tìm giá trị nhỏ nhất của biểu thức
 Xem đáp án
Xem đáp án
Phương pháp:
- Sử dụng: G là trọng tâm tam giác ABC ta có:
- Khoảng cách từ điểm đến mặt phẳng là
Cách giải:
Gọi G là trọng tâm tam giác ABC ta có G(1; 2; 1).
Ta có:
Do đó là hình chiếu của G lên (P). Khi đó
Vậy
Chọn A.
Câu 48:
Cho hàm số f(x) có đạo hàm cấp hai trên Biết f(0) và hàm số y = f'(x) có đồ thị như hình vẽ bên. Phát biểu nào sau đây đúng?
 Xem đáp án
Xem đáp án
Phương pháp:
- Sử dụng: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), y = g(x), đường thẳng x = a, x = b là Tính từ đó so sánh f(3), f'(3).
- Từ đồ thị hàm số f'(x) suy ra BXD hàm số f''(x) so sánh f''(3) với 0.
Cách giải:
Dựa vào đồ thị hàm số ta có f'(3) = 0.
Ta có nên
Xét hàm số f'(x) trên , hàm số có 2 điểm cực trị
Ta có BXD f''(x) như sau:
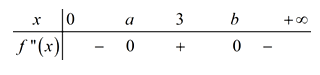
Vậy
Chọn C.
Câu 49:
 Xem đáp án
Xem đáp án
Phương pháp:
- Sử dụng
- Chia cả 2 vế cho
- Đặt ẩn phụ đưa về bất phương trình bậc hai ẩn t
- Giải bất phương trình tìm t sau đó tìm x
Cách giải:
Ta có:
Đặt bất phương trình trở thành:
Kết hợp điều kiện
Chọn C.
Câu 50:
Tính tổng các nghiệm của phương trình
 Xem đáp án
Xem đáp án
Phương pháp:
Xét hàm đặc trưng.
Cách giải:
ĐKXĐ:
Ta có:
Xét hàm đặc trưng có nên hàm số đồng biến trên suy ra
Vậy tổng các nghiệm của phương trình đã cho là
Chọn B.
