30 đề thi thử THPT Quốc gia môn Toán năm 2022 có lời giải - Đề 11
-
2819 lượt thi
-
50 câu hỏi
-
120 phút
Danh sách câu hỏi
Câu 1:
Cho khối chóp S.ABC trên ba cạnh SA,SB, SC lần lượt lấy ba điểm A'B'C' sao cho Gọi V,V' lần lượt là thể tích của các khối chóp S.ABC và S.A'B'C'. Khi đó tỉ số là
 Xem đáp án
Xem đáp án
Chọn A.
Áp dụng công thức tỉ số thể tích
Câu 2:
Một chất điểm chuyển động theo quy luật với t là thời gian tính từ lúc bắt đầu chuyển động, s(t) là quãng đường đi được trong khoảng thời gian t. Tính thời điểm t tại đó vận tốc đạt giá trị lớn nhất.
 Xem đáp án
Xem đáp án
Chọn B.
Biểu thức vận tốc của chuyển động là
Vận tốc đạt giá trị lớn nhất bằng 12 khi t = 2
Câu 3:
Đồ thị hàm số và đồ thị hàm số có bao nhiêu điểm chung?
 Xem đáp án
Xem đáp án
Chọn D.
Xét phương trình
Vậy hai đồ thị có hai điểm chung.
Câu 4:
Cho hàm số f(x) có đạo hàm Tìm số điểm cực trị của hàm số f(x).
 Xem đáp án
Xem đáp án
Chọn B.
Ta có:
Bảng biến thiên
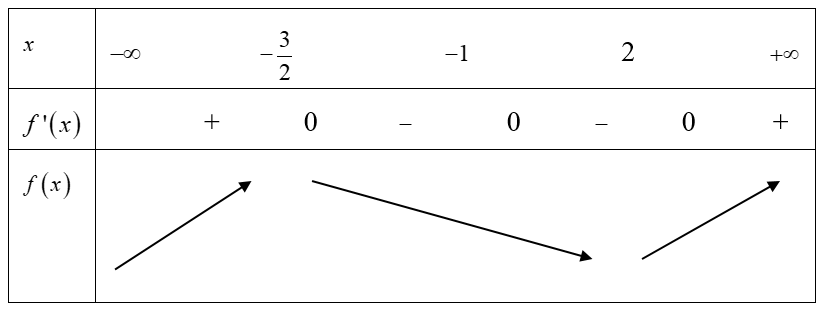
Vậy hàm số f(x) có hai điểm cực trị.
Câu 6:
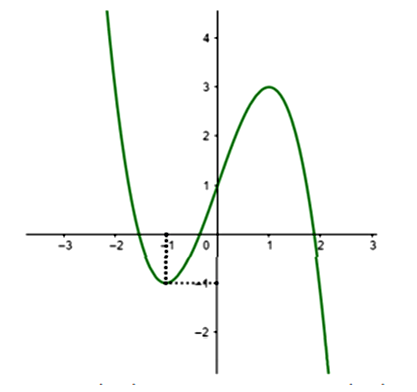
Cho hàm số có đồ thị như hình vẽ bên
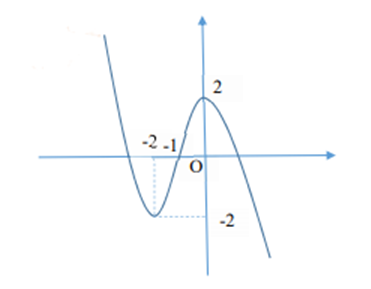
Tìm tập hợp S tất cả các giá trị của tham số thực m sao cho phương trình có ba nghiệm thực phân biệt.
 Xem đáp án
Xem đáp án
Chọn C.
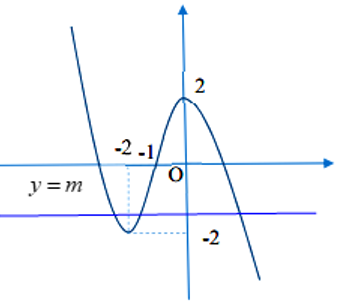
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số và y = m. Dựa vào đồ thị trên suy ra phương trình đã cho có 3 nghiệm phân biệt
Câu 8:
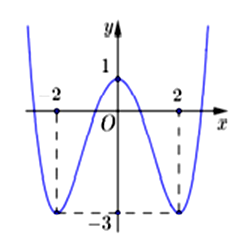
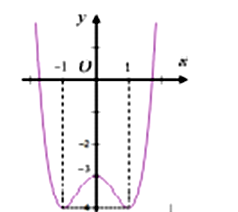
Đường cong sau đây là đồ thị hàm số nào dưới đây
 Xem đáp án
Xem đáp án
Chọn D.
Từ các phương án của đề bài và từ hình dạng đồ thị đã cho ta nhận thấy đó là đồ thị của hàm số với a > 0 nên loại phương án A, C và đồ thị giao trục tung tại điểm có tung độ - 3 nên loại phương án B.
Câu 9:
Số tiếp tuyến của đồ thị hàm số song song với trục hoành là
 Xem đáp án
Xem đáp án
Chọn A.
Ta có
Vì tiếp tuyến song song với trục hoành nên hệ số góc bằng 0. Xét phương trình:
Vậy có 2 tiếp tuyến của đồ thị hàm số song song với trục hoành.
Câu 10:
Tìm tất cả các giá trị của tham số m để đồ thị hàm số có tiệm cận đứng?
 Xem đáp án
Xem đáp án
Chọn A.
Tập xác định
Đồ thị hàm số đã cho có tiệm cận đứng
không là nghiệm của phương trình
Câu 11:
Cho hàm số y= f(x) có bảng biến thiên sau:
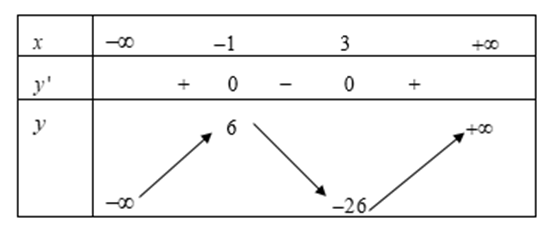
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
 Xem đáp án
Xem đáp án
Chọn D.
Dựa vào bảng biến thiên ta thấy hàm số đã cho nghịch biến trên khoảng
Câu 13:
Có 10 cái bút khác nhau và 8 quyển sách giáo khoa khác nhau. Một bạn học sinh cần chọn một cái bút và một quyển sách. Hỏi bạn học sinh đó có bao nhiêu cách chọn?
 Xem đáp án
Xem đáp án
Chọn D.
Bạn học sinh có 10 cách chọn 1 cái bút và 8 cách chọn 1 quyển sách. Vậy theo quy tắc nhân bạn ấy có 10.8=80 cách chọn một quyển sách và một cái bút.
Câu 14:
Đồ thị hàm số nào dưới đây có tiệm cận đứng?
 Xem đáp án
Xem đáp án
Chọn C.
Các hàm số và có tập xác định nên không có tiệm cận đứng.
Hàm số có tập xác định và nên x = 0 là đường tiệm cận đứng của hàm số.
Câu 15:
 Xem đáp án
Xem đáp án
Chọn D.
Ta có
Vậy hệ số góc của tiếp tuyến của đồ thị hàm số tại điểm M(-2;2) là
Câu 16:
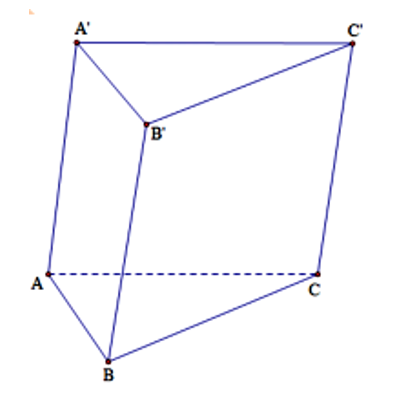
Lăng trụ tam giác đều có độ dài tất cả các cạnh bằng 3. Thể tích khối lăng trụ đã cho bằng
 Xem đáp án
Xem đáp án
Chọn A.
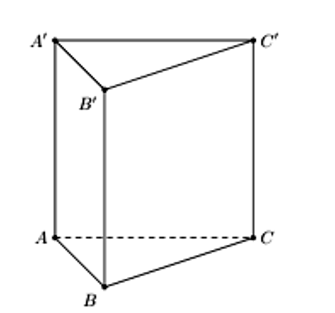
Lăng trụ tam giác đều là lăng trụ đứng có đáy là tam giác đều.
Vậy thể tích khối lăng trụ đã cho là (đvtt).
Câu 18:
Cho hàm số y= f(x) có tập xác định và bảng xét dấu đạo hàm như sau

Số điểm cực trị của hàm số đã cho là
 Xem đáp án
Xem đáp án
Chọn A.
Hàm số y = f(x) có tập xác định nên có hai cực trị tại x = 2 và x = -2
Câu 19:
Đồ thị (C) của hàm số và đường thẳng cắt nhau tại 2 điểm A và B. Khi đó độ dài đoạn AB bằng?
 Xem đáp án
Xem đáp án
Chọn B.
Phương trình hoành độ giao điểm của (C) và d là
Suy ra
Ta được
Câu 20:
Thể tích của khối chóp tứ giác đều có chiều cao bằng và cạnh đáy bằng là:
 Xem đáp án
Xem đáp án
Chọn D.
· Diện tích đáy là:
· Thể tích khối chóp tứ giác đều:
Câu 21:
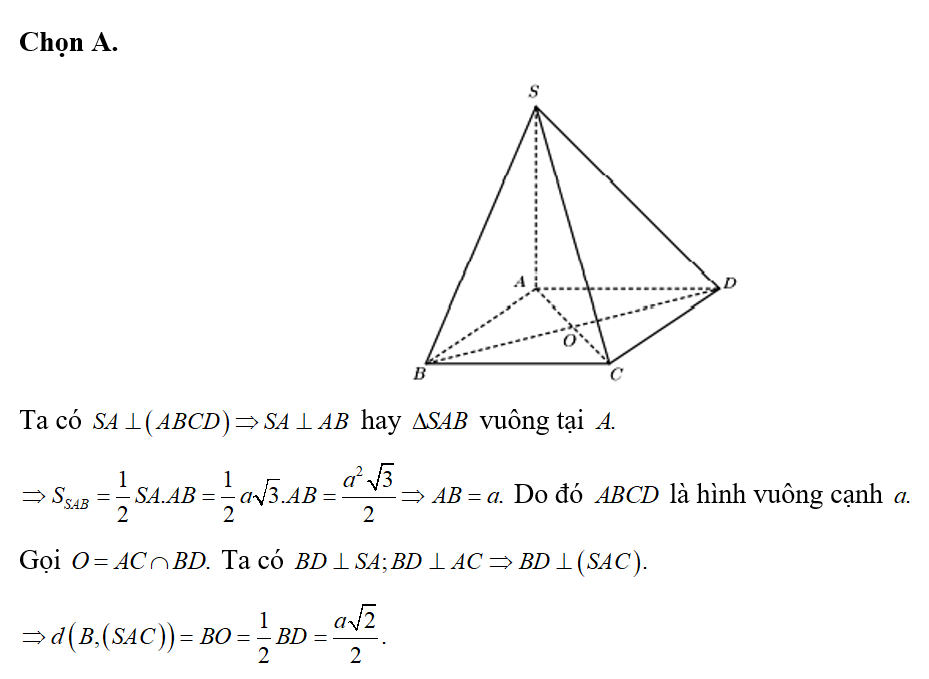
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a cạnh bên SA vuông góc với mặt phẳng đáy (ABCD) và SA= 3a. Thể tích khối chóp S.ABCD bằng:
 Xem đáp án
Xem đáp án
Chọn C.
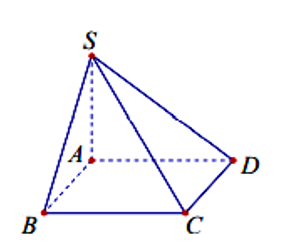
Ta có là đường cao của hình chóp.
Thể tích khối chóp
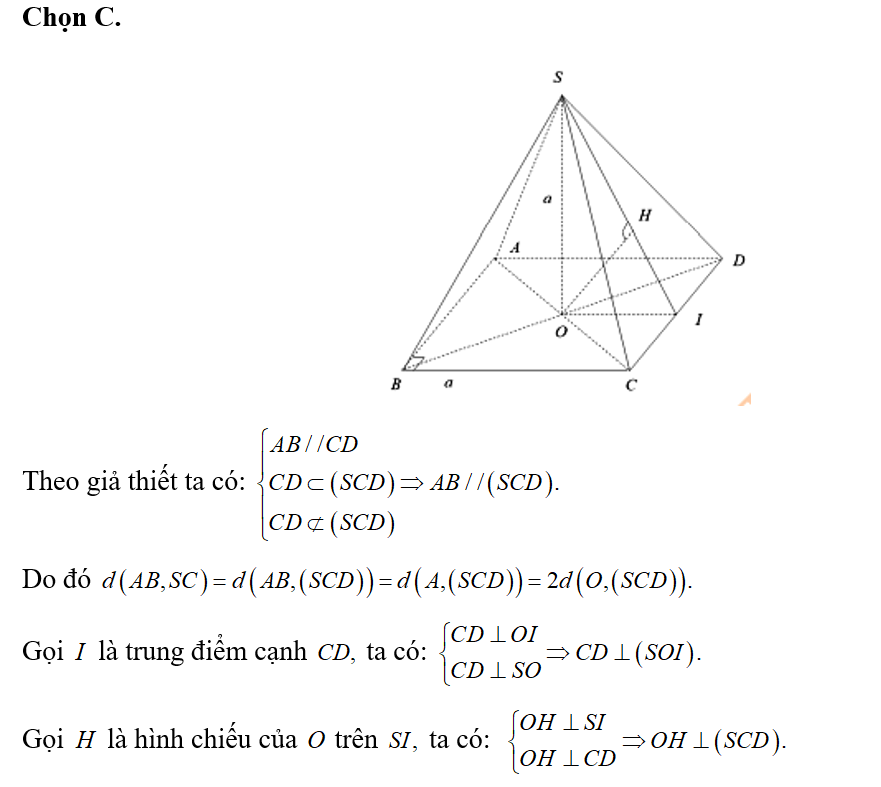
Câu 22:
Mặt phẳng chia khối lăng trụ thành hai khối chóp:
 Xem đáp án
Xem đáp án
Chọn D.
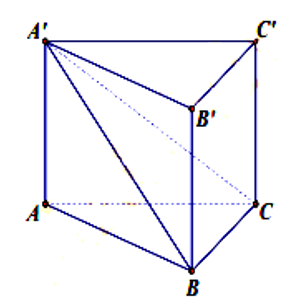
Mặt phẳng chia khối lăng trụ thành hai khối chóp và
Câu 23:
Đường tiệm cận ngang của đồ thị hàm số là
 Xem đáp án
Xem đáp án
Chọn D.
Tập xác định
Ta có:
Suy ra đồ thị hàm số đã cho có đường tiệm cận ngang là:
Câu 25:
Hình bên là đồ thị của hàm số y = f'(x) .Hỏi hàm số f(x) đồng biến trên khoảng nào dưới đây
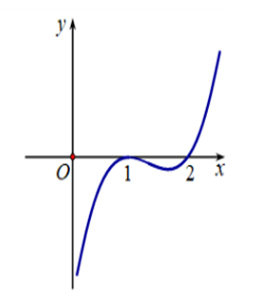
 Xem đáp án
Xem đáp án
Chọn B.
Từ đồ thị của hàm số y = f'(x) ta có bảng sau:
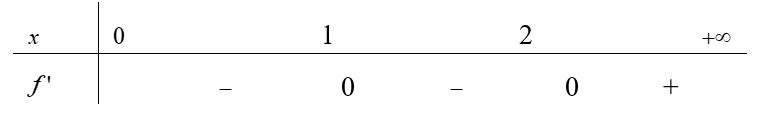
Từ bảng xét dấu trên, ta suy ra hàm số y= f(x) đồng biến trên
Câu 26:
Đồ thị hàm số có hai điểm cực trị và Tính y(-1)
 Xem đáp án
Xem đáp án
Chọn C.
Ta có
Điểm và là hai điểm cực trị nên
Suy ra Vậy
Câu 28:
Cho hàm số có đồ thị như hình vẽ. Mệnh đề nào dưới đây đúng?
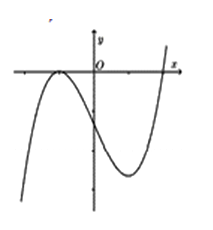
 Xem đáp án
Xem đáp án
Chọn B.
Nhìn vào đồ thị ta thấy nhánh cuối đi lên nên a > 0
Giao điểm của đồ thị với trục Oy nằm phía dưới Ox nên d < 0
Câu 29:
Cho hàm số f(x) xác định và có đạo hàm cấp một và cấp hai trên khoảng (a;b) và Khẳng định nào sau đây sai ?
 Xem đáp án
Xem đáp án
Chọn D.
Câu 31:
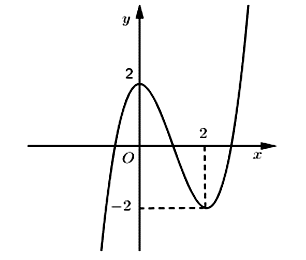
Đường cong trong hình vẽ bên là đồ thị của hàm số nào?
 Xem đáp án
Xem đáp án
Chọn B.
Từ đồ thị hàm số, ta có: chỉ có đáp án B thỏa mãn.
Câu 34:
 Xem đáp án
Xem đáp án
Chọn A.
Vì nên A là đáp án sai.
Câu 36:
Cho hàm số có đồ thị như hình bên dưới.
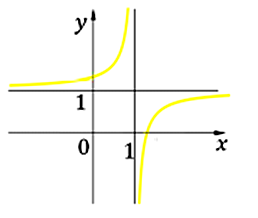
Xét các mệnh đề sau:
(I) Hàm số đồng biến trên các khoảng và
(II) Hàm số nghịch biến trên các khoảng và
(III) Hàm số đồng biến trên tập xác định.
Số các mệnh đề đúng là:
 Xem đáp án
Xem đáp án
Chọn C.
Dựa vào đồ thị ta có hàm số đồng biến trên và
Câu 37:
Trong các hàm số sau, hàm số nào đồng biến trên R ?
 Xem đáp án
Xem đáp án
Chọn B.
Cách 1: Xét hàm số ta có:
TXĐ: D = R
Vậy hàm số đồng biến trên R.
Cách 2:
Do hàm số đồng biến trên R nên loại A;D vì hai hàm số này không có tập xác định là R.
Loại C vì đây là hàm trùng phương.
Vậy chọn B.
Câu 38:
Cho hàm số y = f(x) có bảng biến thiên như sau:
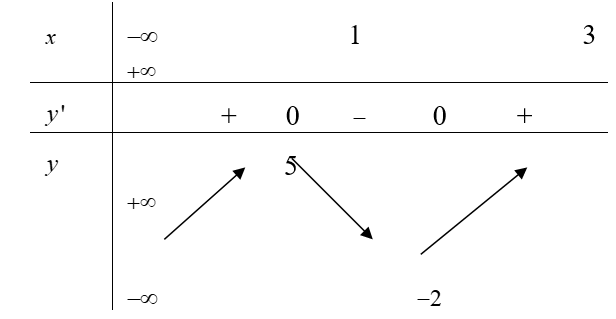
Số nghiệm thực của phương trình là:
 Xem đáp án
Xem đáp án
Chọn D.
Ta có: Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y = f(x) và đường thẳng
Dựa vào bảng biền thiên của y = f(x), ta có đồ thị y= f(x) cắt đường thẳng tại 3 điểm phân biệt. Vậy số nghiệm thực của phương trình là 3.
Câu 40:
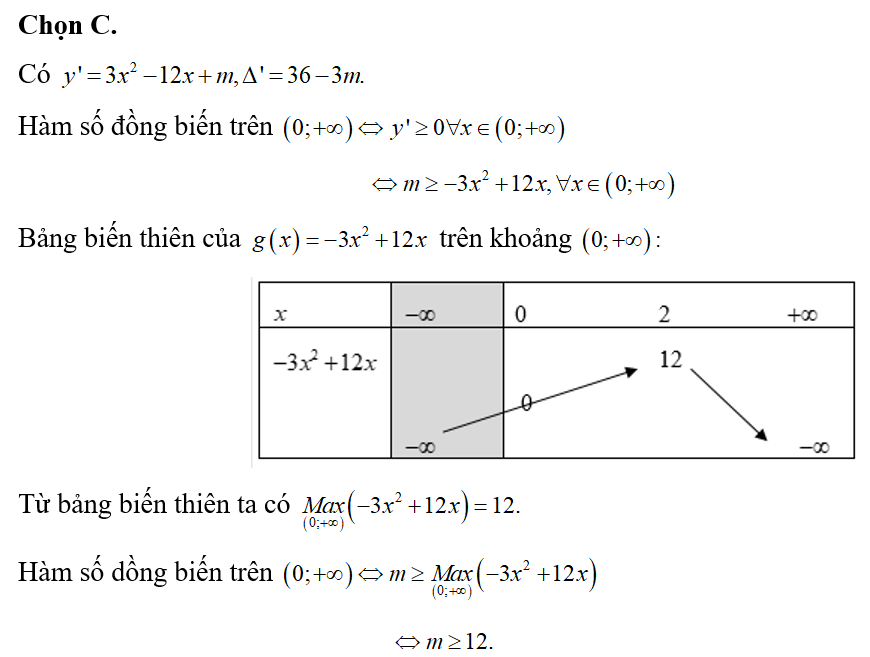
Tìm giá trị lớn nhất của tham số m để hàm số đồng biến trên R
 Xem đáp án
Xem đáp án
Chọn D.
Tập xác định D = R
Ta có:
Hàm số đồng biến trên
Giá trị lớn nhất của tham số m để hàm số đồng biến trên R thì m = 2
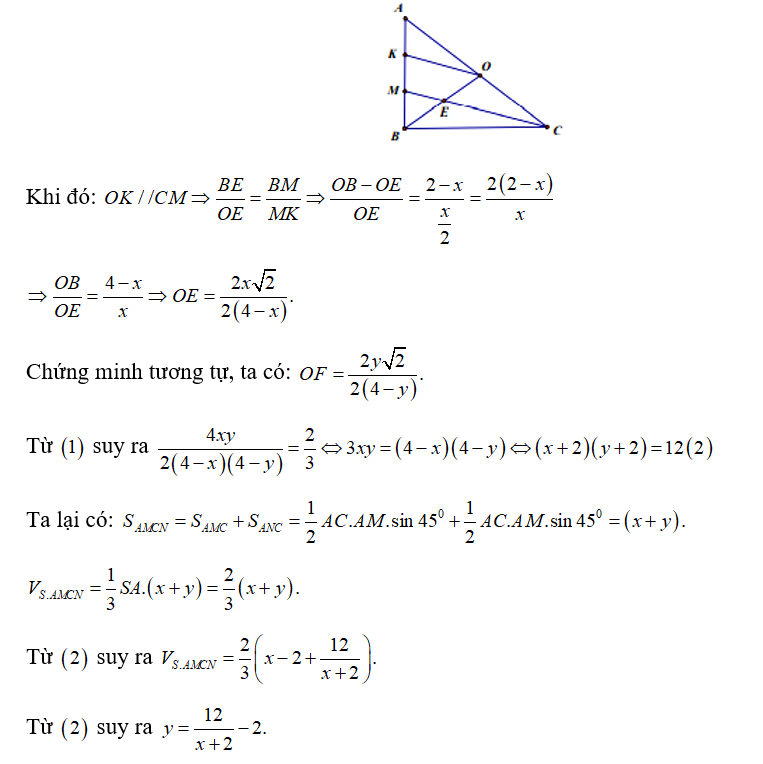
Câu 41:
Cho hình lăng trụ ABC.A'B'C'. Gọi M,N,P lần lượt là các điểm thuộc cạnh AA',BB',CC' sao cho Gọi lần lượt là thể tích của hai khối đa diện ABCMNP và Tính tỉ số
 Xem đáp án
Xem đáp án
Chọn A.
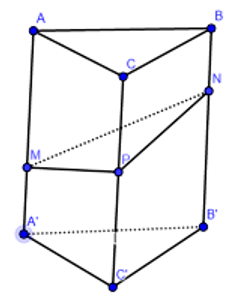
Suy ra
Câu 45:
Một hộp đựng 2020 tấm thẻ được đánh số từ 1 đến 2020. Bạn Dũng rút ngẫu nhiên cùng lúc ba tấm thẻ. Hỏi bạn Dũng có bao nhiêu cách rút sao cho bất kỳ hai trong ba tấm thẻ được lấy ra đó có hai số tương ứng ghi trên hai tấm thẻ luôn hơn kém nhau ít nhất hai đơn vị?
 Xem đáp án
Xem đáp án
Chọn B.
Số cách chọn 3 tấm thẻ tùy ý là:
Cách rút không thỏa bài toán là dãy ba số rút ra có ít nhất hai số liên tiếp
Bộ hai số liên tiếp là:
Suy ra số cách rút ra ba tấm thẻ mà có hai số liên tiếp là:
Rút ra bộ ba số liên tiếp là:
Trong cách rút ra ba tấm thẻ có hai số liên tiếp có trường hợp rút ra ba tấm liên tiếp (lặp 2 lần).
Vậy số cách rút thỏa yêu cầu là:
Câu 47:
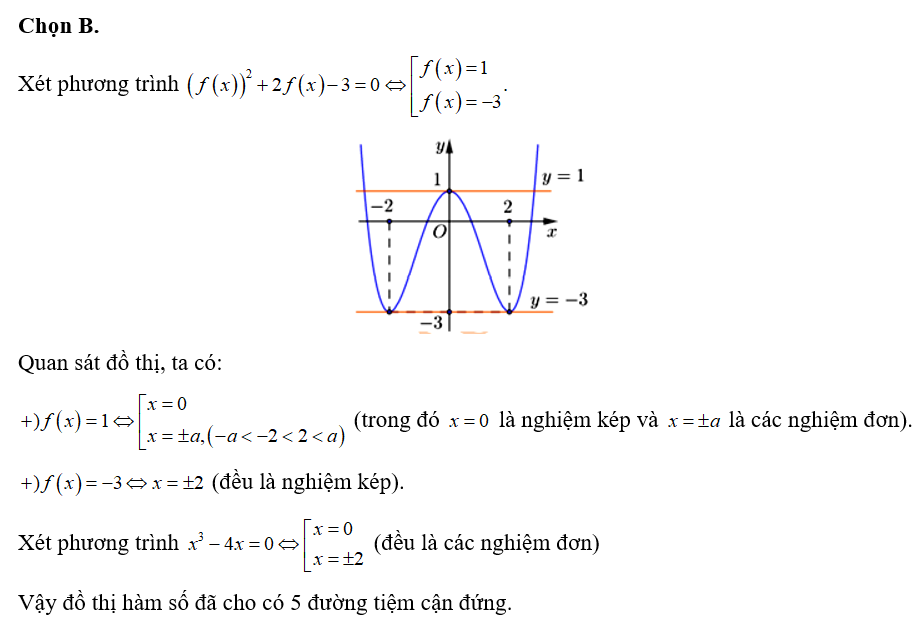
Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ.
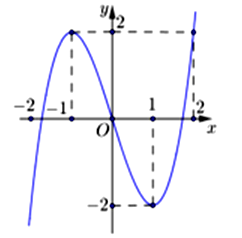
Có bao nhiêu giá trị nguyên của tham số m để phương trình có nghiệm
 Xem đáp án
Xem đáp án
Chọn A.
Ta có
Quan sát đồ thị, suy ra
Phương trình có nghiệm khi và chỉ khi
Vậy có 4 giá trị nguyên của tham số m thỏa mãn là