50 câu hỏi trắc nghiệm thuộc 30 đề thi thử THPT Quốc gia môn Toán năm 2022 có lời giải - Đề 5

Câu 1:

Hàm số nào sau đây đồng biến trên $ℝ ?$

A. $y = x^{3} - x + 2.$

B. $y = x^{3} - 3 x + 5.$

C. $y = x^{3} + x - 1.$

D. $y = x^{4} + 4.$

Xem đáp án

Chọn C.

Ta có $y = x^{3} + x - 1 \Leftrightarrow y' = 3 x^{2} + 1 > 0 \forall x \in ℝ .$

Câu 2:

Cho hàm số y= f(x) có bảng xét dấu của y' như sau:

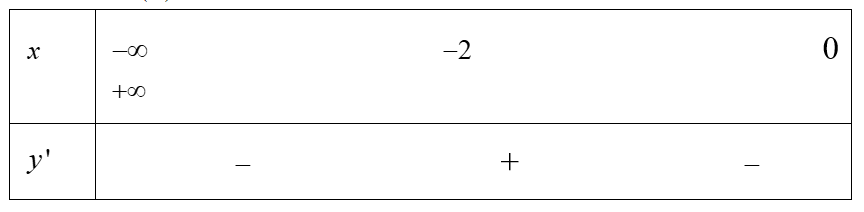
Hàm số đồng biến trên khoảng nào dưới đây?

A. $(- \infty; - 2) .$

B. $(- 3; 1) .$

C. $(0; + \infty) .$

D. (-2;0)

Xem đáp án

Chọn D.

Căn cứ vào bảng xét dấu ta có hàm số đồng biến trên khoảng (-2;0)

Câu 3:

Cho biểu thức

P = \sqrt[4]{x^{5}},

với x > 0 Mệnh đề nào sau đây đúng?

A. $P = x^{\frac{5}{4}} .$

B. $P = x^{\frac{4}{5}} .$

C. $P = x^{20} .$

D. $P = x^{9} .$

Xem đáp án

Chọn A.

Áp dụng định lý lũy thừa với số mũ hữu tỉ ta được $P = x^{\frac{5}{4}} .$

Câu 4:

Tiệm cận ngang của đồ thị hàm số

y = \frac{x + 1}{2 x - 4}

có phương trình là

A. y = -2

B. $y = \frac{1}{2} .$

C. $y = - \frac{1}{4} .$

D. y = -1

Xem đáp án

Chọn B.

$\lim_{x \to + \infty} \frac{x + 1}{2 x - 4} = \frac{1}{2} .$

$\lim_{x \to - \infty} \frac{x + 1}{2 x - 4} = \frac{1}{2}$

Vậy đường thẳng $y = \frac{1}{2}$ là tiệm cận ngang của đồ thị hàm số $y = \frac{x + 1}{2 x - 4} .$

Câu 5:

Cho khối nón có bán kính đáy $r = \sqrt{3}$ và chiều cao h=4 Tính thể tích V của khối nón đã cho.

A. V= 4

B. $V = 4 π .$

C. V= 12

D. $V = 12 π .$

Xem đáp án

Chọn B.

Ta có khối nón có thể tích $V = \frac{1}{3} π r^{2} h = \frac{1}{3} π .3.4 = 4 π .$

Câu 6:

Cho hàm số y= f(x) có đạo hàm $f' (x) = (x + 2) x^{2} {(x - 1)}^{3}$ với $\forall x \in ℝ .$ Hàm số đã cho có bao nhiêu điểm cực trị.

A. 2.

B. 0.

C. 3.

D. 1.

Xem đáp án

Chọn A.

Ta có bảng biến thiên:

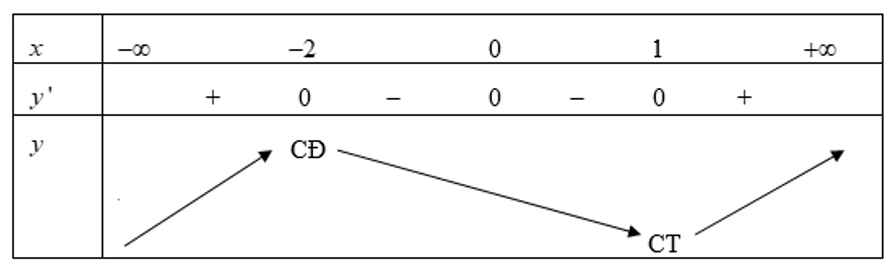
Cho hàm số y= f(x) có đạo hàm f'(x)= (x+2)x^2(x-1)^3 với với mọi x thuộc R. Hàm số đã cho có bao nhiêu điểm cực trị. (ảnh 1)

Nhìn vào bảng biến thiên suy ra hàm số y= f(x) có 2 điểm cực trị.

Câu 7:

Cho hàm số y = f(x) có bảng biến thiên như sau

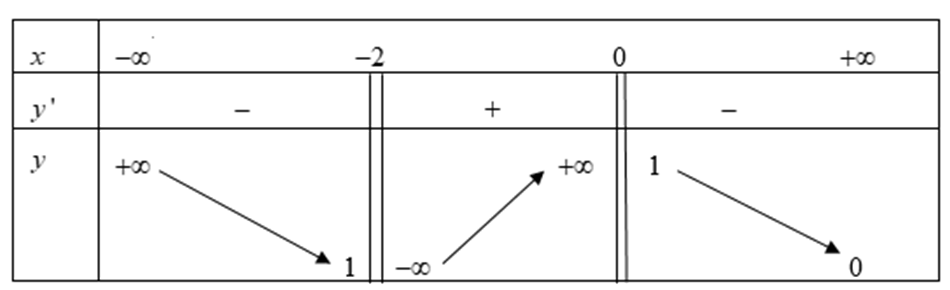
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho bằng?

A. 2.

B. 1.

C. 0.

D. 3.

Xem đáp án

Chọn A.

Ta có bảng biến thiên:

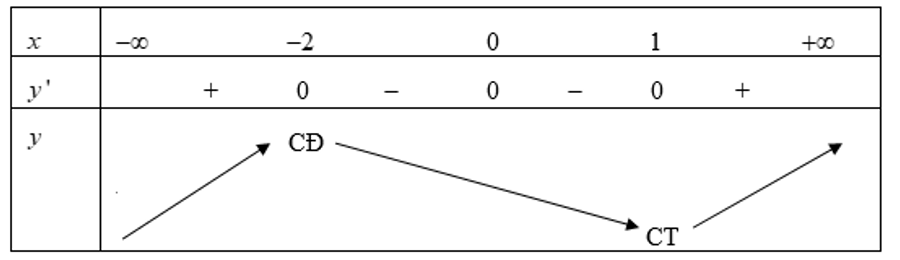
Cho hàm số y = f(x) có bảng biến thiên như sau Tổng số đường tiệm cận đứng và tiệm cận ngang của (ảnh 2)

Nhìn vào bảng biến thiên suy ra hàm số y = f(x) có 2 điểm cực trị.

Câu 8:

Tập nghiệm của bất phương trình ${(\frac{1}{2})}^{x - 1} \geq 128$ là?

A. $[6; + \infty) .$

B. $[8; + \infty) .$

C. $(- \infty; 8] .$

D. $(- \infty; - 6] .$

Xem đáp án

Chọn D.

$\lim_{x \to + \infty} y = 0 \Rightarrow$ tiệm cận ngang là y = 0-

$\lim_{x \to {(- 2)}^{+}} y = - \infty \Rightarrow$ tiệm cận đứng là x = -2

$\lim_{x \to 0^{-}} y = + \infty \Rightarrow$ tiệm cận đứng là x= 0

Vậy tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số bằng 3.

Câu 9:

Điều kiện xác định của hàm số $y = \log_{2} (x - 1)$ là

A. $\forall x \in ℝ .$

B. x > 1

C. $x \neq 1.$

D. x < 1

Xem đáp án

Chọn D.

${(\frac{1}{2})}^{x - 1} \geq 128 \Leftrightarrow x - 1 \leq - 7 \Leftrightarrow x \leq 6.$

Vậy tập nghiệm của bất phương trình là $S = (- \infty; - 6] .$

Câu 10:

Cho hàm số y = f(x) có bảng biến thiên sau

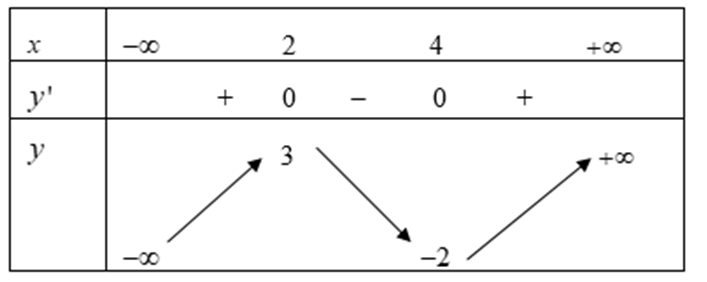
Giá trị cực đại của hàm số đã cho bằng

A. 4.

B. 2.

C. 3.

D. -2

Xem đáp án

Chọn B.

Hàm số đã cho xác định khi: $x - 1 > 0 \Leftrightarrow x > 1.$

Vậy điều kiện xác định của hàm số $y = \log_{2} (x - 1)$ là: x > 1

Câu 11:

Hàm số $y = \frac{1}{3} x^{3} + x^{2} - 3 x + 1$ đạt cực tiểu tại điểm

A. $x = - 3.$

B. $x = 3.$

C. $x = - 1 .$

D. $x = 1 .$

Xem đáp án

Chọn D.

Ta có $y' = x^{2} + 2 x - 3; y' = 0 \Leftrightarrow [\begin{array}{l} x = - 3 \\ x = 1 \end{array}; y " = 2 x + 2; y " (- 3) = - 4 < 0; y " (1) = 4 > 0.$

Suy ra hàm số đạt cực tiểu tại điểm x= 1

Câu 12:

Phương trình $\log_{2} (3 x - 2) = 2$ có nghiệm là

A. $x = \frac{2}{3} .$

B. x = 2

C. x = 1

D. $x = \frac{4}{3} .$

Xem đáp án

Chọn B.

ĐKXĐ: $3 x - 2 > 0 \Leftrightarrow x > \frac{2}{3} .$

Ta có $\log_{2} (3 x - 2) = 2 \Leftrightarrow 3 x - 2 = 4 \Leftrightarrow x = 2$ (thỏa mãn ĐKXĐ).

Câu 13:

Đồ thị sau là đồ thị của hàm số nào dưới đây?

A. $y = \frac{x}{2 x + 1} .$

B. $y = \frac{x + 1}{2 x + 1} .$

C. $y = \frac{x - 1}{2 x + 1} .$

D. $y = \frac{x + 3}{2 x + 1} .$

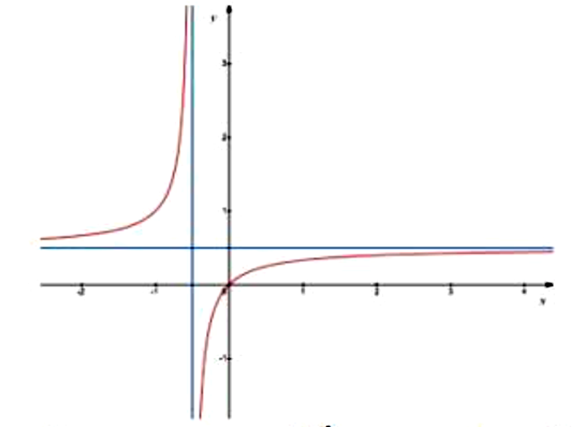
Xem đáp án

Chọn A.

Đồ thị hàm số đã cho đi qua gốc tọa độ.

Đối chiếu với đáp án ta chọn được đáp án A.

Câu 14:

Phương trình $3^{x - 4} = 1$ có nghiệm là:

A. x = 5

B. x = 0

C. x = 4

D. x = -4

Xem đáp án

Chọn C.

Ta có: $3^{x - 4} = 1 \Leftrightarrow 3^{x - 4} = 3^{0} \Leftrightarrow x - 4 = 0 \Leftrightarrow x = 4.$

Câu 15:

Cho khối lăng trụ đứng có diện tích đáy bằng $2 a^{2}$ và cạnh bên bằng 3a.Thể tích khối lăng trụ đã cho bằng

A. $2 a^{3} .$

B. $3 a^{3} .$

C. $18 a^{3} .$

D. $6 a^{3} .$

Xem đáp án

Chọn D.

Thể tích khối lăng trụ đã cho bằng $V = B . h = 2 a^{2} .3 a = 6 a^{3}$ (đvtt).

Câu 16:

Cho hàm số y = f(x) xác định trên R, có bảng biến thiên như sau

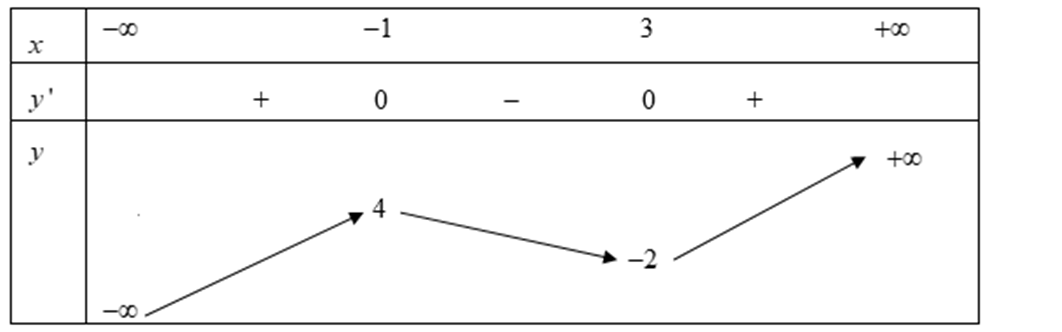
Hàm số y = f(x) đạt cực đại tại điểm

A. x= -1

B. x= 4

C. x= 3

D. x= -2

Xem đáp án

Chọn A.

Hàm số đã cho đạt cực đại tại điểm x = -1

Câu 17:

Cho hàm số $y = x^{3} + 5 x + 7.$ Giá trị lớn nhất của hàm số trên đoạn [-5;0] bằng bao nhiêu ?

A. 7.

B. 5.

C. 80.

D. -143

Xem đáp án

Chọn A.

Ta có $y' = 3 x^{2} + 5 > 0, \forall x \in ℝ \Rightarrow$ Hàm số đã cho đồng biến trên [5;0]

$\Rightarrow \max_{[- 5; 0]} y = y (0) = 7.$

Câu 18:

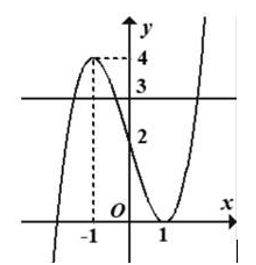
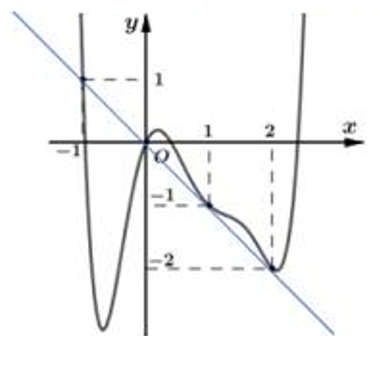
Cho hàm số y = f(x) có đồ thị (C) như hình vẽ. Số giao điểm của (C) và đường thẳng y = 3 là

A. 2.

B. 0.

C. 3.

D. 1.

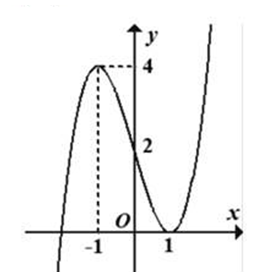
Xem đáp án

Chọn C.

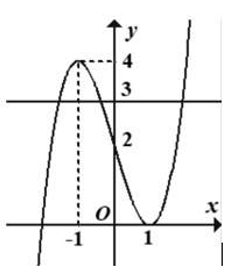
Cho hàm số y = f(x) có đồ thị (C) như hình vẽ. Số giao điểm của (C) và đường thẳng y = 3 là (ảnh 2)

Số giao điểm của (C) và đường thẳng y = 3 bằng 3.

Câu 19:

Tiệm cận đứng của đồ thị hàm số $y = \frac{3 x - 5}{x - 2}$ là

A. x = 2

B. x = 3

C. y = 3

D. y = 2

Xem đáp án

Chọn C.

Tiệm cận đứng của đồ thị hàm số y= 3x-5/ x-2 là (ảnh 1)

Số giao điểm của (C) và đường thẳng y=3 bằng 3.

Câu 20:

Hàm số nào sau đây đồng biến trên khoảng

(- \infty; + \infty) ?

A. $y = {(\frac{e}{4})}^{x} .$

B. $y = {(\frac{2}{3})}^{x} .$

C. $y = {(\frac{π}{3})}^{x} .$

D. $y = {(\frac{3}{4})}^{x} .$

Xem đáp án

Chọn C.

Vì $\frac{π}{3} > 1$ nên hàm số $y = {(\frac{π}{3})}^{x}$ luôn đồng biến trên R

Câu 21:

Thể tích khối cầu đường kính 2a bằng

A. $4 π a^{3} .$

B. $\frac{4 π a^{3}}{3} .$

C. $2 π a^{3} .$

D. $\frac{12 π a^{3}}{3} .$

Xem đáp án

Chọn B.

Bán kính mặt cầu: R= a

Thể tích khối cầu: $V = \frac{4}{3} π . R^{3} = \frac{4}{3} π a^{3} .$

Câu 22:

Cho hình trụ có bán kính đáy bằng 5 và chiều cao bằng 7. Diện tích xung quanh của hình trụ đã cho bằng

A. $175 π .$

B. $\frac{175 π .}{3}$

C. $35 π .$

D. $70 π .$

Xem đáp án

Chọn D.

Ta có: r = 5 và l = 7

Diện tích xung quanh của hình trụ: $S_{x q} = 2 π r l = 2 π .5.7 = 70 π .$

Câu 23:

Gọi m là giá trị nhỏ nhất và M là giá trị lớn nhất của hàm số $y = x^{4} - 2 x^{2} - 3$ trên đoạn [0;2] Giá trị biểu thức M + m bằng

A. 2.

B. 1.

C. -3

D. -7

Xem đáp án

Chọn B.

$y' = 4 x^{3} - 4 x = 0 \Leftrightarrow [\begin{array}{l} x = 0 \notin (0; 2) \\ x = 1 \in (0; 2) \\ x = - 1 \notin (0; 2) \end{array}$

$y (1) = - 4, y (0) = - 3, y (2) = 5$

Suy ra $M = 5, m = - 4$

Vậy $M + m = 5 - 4 = 1.$

Câu 24:

Số cạnh của một hình tứ diện là

A. 6.

B. 12.

C. 4.

D. 8.

Xem đáp án

Chọn A.

Câu 25:

Thể tích khối chóp có diện tích đáy bằng $\frac{\sqrt{3}}{2}$ và chiều cao bằng $\frac{2 \sqrt{3}}{3}$ là

A. 1.

B. $\frac{\sqrt{6}}{6} .$

C. $\frac{1}{3} .$

D. $\frac{\sqrt{2}}{3} .$

Xem đáp án

Chọn C.

Thể tích khối chóp: $V = \frac{1}{3} B . h = \frac{1}{3} . \frac{\sqrt{3}}{2} . \frac{2 \sqrt{3}}{3} = \frac{1}{3} .$

Câu 26:

Có bao nhiêu giá trị nguyên dương của tham số m để hàm số $y = x^{3} - 3 m x^{2} + 3 (m^{2} - 2) x$ đồng biến trên khoảng $(12; + \infty) ?$

A. 10.

B. 0.

C. 13.

D. 11.

Xem đáp án

Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y= x^3-3mx^2+ 3(m^2-2)x (ảnh 1)

Câu 27:

Tìm tất cả các giá trị thực của tham số m để hàm số $y = \frac{4}{3} \sin^{3} 2 x + 2 \cos^{2} 2 x - (m^{2} + 3 m) \sin 2 x - 1$ nghịch biến trên khoảng $(0; \frac{π}{4}) .$

A. $m \leq \frac{- 3 - \sqrt{5}}{2}$ hoặc $m \geq \frac{- 3 + \sqrt{5}}{2} .$

B. $m \leq - 3$ hoặc $m \geq 0.$

C.

- 3 \leq m \leq 0.

D.

\frac{- 3 - \sqrt{5}}{2} \leq m \leq \frac{- 3 + \sqrt{5}}{2} .

Xem đáp án

Chọn D.

Ta có $y = \frac{4}{3} \sin^{3} 2 x + 2 \cos^{2} 2 x - (m^{2} + 3 m) \sin 2 x - 1$ hay $y = \frac{4}{3} \sin^{3} 2 x - 2 \sin^{2} 2 x - (m^{2} + 3 m) \sin 2 x + 1$ do vậy

$y' = 2 [4 \sin^{2} 2 x - 4 \sin 2 x - (m^{2} + 3 m)] \cos 2 x .$

Với $\forall x \in (0; \frac{π}{4})$ ta có $\cos 2 x > 0$ vì vậy hàm số đã cho nghịch biến trên khoảng $(0; \frac{π}{4})$ khi và chỉ khi

$y' \geq 0, \forall x \in (0; \frac{π}{4}) \Leftrightarrow 4 \sin^{2} 2 x - 4 \sin 2 x - (m^{2} + 3 m) \geq 0, \forall x \in (0; \frac{π}{4}) .$

Đặt $t = \sin 2 x$ với $\forall x \in (0; \frac{π}{4})$ ta được $t \in (0; 1)$ do vậy ta có bất phương trình

$4 t^{2} - 4 t - (m^{2} + 3 m) \geq 0, \forall t \in (0; 1) \Leftrightarrow 4 t^{2} - 4 t \geq m^{2} + 3 m, \forall t \in (0; 1) .$

Xét hàm số $g (t) = 4 t^{2} - 4 t$ ta có bảng biến thiên như sau

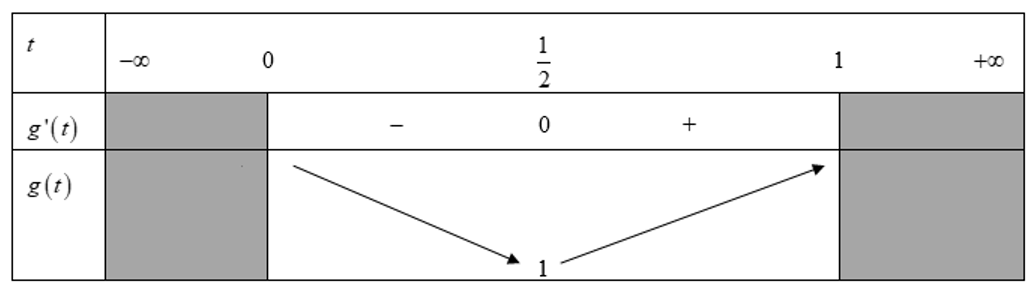
Tìm tất cả các giá trị thực của tham số m để hàm số y= 4/3 sin^3 2x+ 2 cos ^2 2x- (m^2+3m) sin 2x-1 (ảnh 1)

Qua bảng ta cần có $m^{2} + 3 m \leq 1 \Leftrightarrow m^{2} + 3 m - 1 \leq 0 \Leftrightarrow \frac{- 3 - \sqrt{5}}{2} \leq m \leq \frac{- 3 + \sqrt{5}}{2} .$

Câu 28:

Hàm số $\log_{2} (4^{x} - 2^{x} + m)$ có tập xác định là $ℝ$ thì

A. $m \geq \frac{1}{4} .$

B. $m = 0 .$

C. $m > \frac{1}{4} .$

D. $m < \frac{1}{4} .$

Xem đáp án

Chọn C.

Hàm số $y = \log_{2} (4^{x} - 2^{x} + m)$ có tập xác định là R khi và chỉ khi $4^{x} - 2^{x} + m > 0, \forall x \in ℝ$

Ta có $4^{x} - 2^{x} + m = {(2^{x})}^{2} - 2^{x} + \frac{1}{4} + m - \frac{1}{4} = {(2^{x} - \frac{1}{2})}^{2} + m - \frac{1}{4} .$

Do vậy $4^{x} - 2^{x} + m \geq m - \frac{1}{4}, \forall x \in ℝ$ suy ra $4^{x} - 2^{x} + m > 0, \forall x \in ℝ \Leftrightarrow m - \frac{1}{4} > 0 \Leftrightarrow m > \frac{1}{4} .$

Vậy hàm số $y = \log_{2} (4^{x} - 2^{x} + m)$ có tập xác định là R thì $m > \frac{1}{4} .$

Câu 29:

Cho khối chóp S. ABCD có thể tích V. Gọi B', C' lần lượt là trung điểm của AB, AC. Tính theo V thể tích khối chóp S. AB'C'

A. $\frac{1}{3} V .$

B. $\frac{1}{2} V .$

C. $\frac{1}{12} V .$

D. $\frac{1}{4} V .$

Xem đáp án

Chọn D.

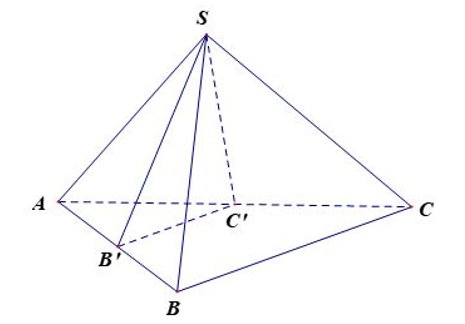
Cho khối chóp S. ABCD có thể tích V. Gọi B', C' lần lượt là trung điểm của AB, AC. Tính theo V (ảnh 1)

Ta có $\frac{V_{S . A B' C'}}{V_{S . A B C}} = \frac{V_{A . S B' C'}}{V_{A . S B C}} = \frac{A S}{A S} . \frac{A B'}{A B} . \frac{A C'}{A C} = 1. \frac{1}{2} . \frac{1}{2} = \frac{1}{4}$

Do đó $V_{S . A B' C'} = \frac{1}{4} V$ .

Câu 30:

Cho hình lăng trụ đứng ABC. A'B'C' có đáy ABC là tam giác vuông tại A. Gọi E là trung điểm AB. Cho biết $A B = 2 a, B C = a \sqrt{3}, C C' = 4 a .$ Khoảng cách giữa hai đường thẳng A'B và CE bằng

A. $\frac{4 a}{7} .$

B. $\frac{12 a}{7} .$

C. $\frac{6 a}{7} .$

D. $\frac{3 a}{7} .$

Xem đáp án

Cho hình lăng trụ đứng ABC. A'B'C' có đáy ABC là tam giác vuông tại A. Gọi E là trung điểm AB. (ảnh 1)

Cho hình lăng trụ đứng ABC. A'B'C' có đáy ABC là tam giác vuông tại A. Gọi E là trung điểm AB. (ảnh 2)

Câu 31:

Ông X gửi vào ngân hàng 60 triệu đồng theo hình thức lãi kép. Lãi suất ngân hàng là 8% trên năm. Sau 5 năm ông X tiếp tục gửi thêm 60 triệu đồng nữa. Hỏi sau 10 năm kể từ lần gửi đầu tiên ông X đến rút toàn bộ tiền gốc và tiền lãi được là bao nhiêu? (Biết lãi suất không thay đổi qua các năm ông X gửi tiền).

A. 217,695 (triệu đồng).

B. 231,815 (triệu đồng).

C. 190,271 (triệu đồng).

D. 197,201 (triệu đồng).

Xem đáp án

Chọn A.

Sau 5 năm đầu tiên số tiền ông X thu về là $T_{1} = 60 {(1 + 8 %)}^{5}$ (triệu đồng).

Số tiền gốc của giai đoạn gửi thứ hai là: $T_{2} = 60 [{(1 + 8 %)}^{5} + 1]$ (triệu đồng).

Tổng số tiền thu về là $T = 60 [{(1 + 8 %)}^{5} + 1] {(1 + 8 %)}^{5} = 217, 695$ (triệu đồng).

Câu 32:

Hàm số $f (x) = \ln \frac{x + 1}{x - 1}$ có đạo hàm là

A. $f' (x) = - \frac{2}{x^{2} + 1} .$

B. $f' (x) = \frac{2}{x^{2} + 1} .$

C. $f' (x) = - \frac{2}{x^{2} - 1} .$

D. $f' (x) = - \frac{x - 1}{x + 1} .$

Xem đáp án

Chọn C.

$f' (x) = {(\frac{x + 1}{x - 1})}^{'} (\frac{x - 1}{x + 1}) = \frac{- 2}{{(x - 1)}^{2}} (\frac{x - 1}{x + 1}) = - \frac{2}{x^{2} - 1} .$

Câu 33:

Tổng tất cả các nghiệm của phương trình $9^{x} - {8.3}^{x} + 15 = 0$ là

A. 15.

B. 8.

C.

\log_{3} 5.

D.

\log_{3} 15.

Xem đáp án

Chọn D.

Ta có $9^{x} - {8.3}^{x} + 15 = 0 \Leftrightarrow (3^{x} - 3) (3^{x} - 5) = 0$

$\Leftrightarrow [\begin{array}{l} 3^{x} = 3 \\ 3^{x} = 5 \end{array} \Leftrightarrow [\begin{array}{l} x = 1 \\ x = \log_{3} 5 \end{array} .$

Câu 34:

Cho a,b,x là các số thực dương thỏa mãn $\log_{2} x = 5 \log_{2} a + 3 \log_{2} b .$ Mệnh đề nào là mệnh đề đúng?

A. $x = a^{5} b^{3} .$

B. $x = 3 a + 5 b .$

C. $x = a^{5} + b^{3} .$

D. $x = 5 a + 3 b .$

Xem đáp án

Chọn A.

Ta có $\log_{2} x = 5 \log_{2} a + 3 \log_{2} b \Leftrightarrow \log_{2} x = \log_{2} a^{5} + \log_{2} b^{3}$

$\Leftrightarrow \log_{2} x = \log_{2} a^{5} b^{3}$

$\Leftrightarrow x = a^{5} b^{3} .$

Câu 35:

Cho hàm số $y = f (x) = \frac{2 - a x}{b x - c} (a, b, c \in ℝ, b \neq 0)$ có bảng biến thiên như sau:

Trong các số a,b,c có bao nhiêu số âm?

A. 2.

B. 1.

C. 0.

D. 3.

Xem đáp án

Cho hàm số y= f(x) = 2-ac/bx-c( a,b,c thuộc R, b khác 0) có bảng biến thiên như sau: Trong các số a,b,c có bao nhiêu số âm? (ảnh 2)

Câu 36:

Cho hàm số $f (x) = x - 3 \sqrt[3]{x + 1} + m,$ đặt $P = \max_{[- 1; 7]} {[f (x)]}^{2} + \min_{[- 1; 7]} {[f (x)]}^{2} .$ Có bao nhiêu giá trị nguyên của m để giá trị của P không vượt quá 26?

A. 6.

B. 7.

C. 4.

D. 5.

Xem đáp án

Cho hàm số f(x)= x- 3 căn bậc ba x+1+ m đặt P= max [-1;7] f(x) ^2+ min [-1;7] f(x) ^2.Có bao nhiêu giá trị (ảnh 1)

Câu 37:

Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật, $A B = 3, A D = 4$ và các cạnh bên của hình chóp tạo với đáy một góc $60^{0}$ .Tính thể tích khối cầu ngoại tiếp hình chóp đã cho.

A. $V = \frac{250 \sqrt{3}}{3} π .$

B. $V = \frac{125 \sqrt{3}}{6} π .$

C. $V = \frac{50 \sqrt{3}}{3} π .$

D. $V = \frac{500 \sqrt{3}}{27} π .$

Xem đáp án

Chọn D.

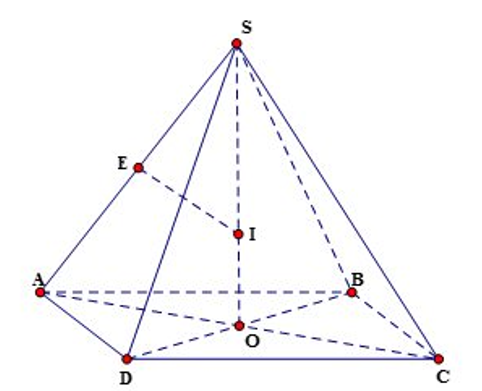
Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật, AB=3, AD=4 và các cạnh bên của hình (ảnh 1)

Gọi $O = A C \cap B D$ khi đó $S O ⊥ (A B C D) \Rightarrow S O$ là trục đường tròn ngoại tiếp đáy ABCD.

Trong mặt phẳng (SAO) gọi giao của đường trung trực của SA với SA là E và SO là I.

Khi đó I là tâm mặt cầu ngoại tiếp S.ABCD. Do đó bán kính là $R = S I = \frac{S A^{2}}{2 S O} (1)$

Do $A O = \frac{A C}{2} = \frac{5}{2}$ và $\hat{S A O} = 60^{0}$ nên $S O = \frac{5 \sqrt{3}}{2}; S A = 5 \Rightarrow R = \frac{5^{2}}{2. \frac{5 \sqrt{3}}{2}} = \frac{5}{\sqrt{3}}$

Thể tích khối cầu $V = \frac{4}{3} π R^{3} = \frac{4}{3} π . {(\frac{5}{\sqrt{3}})}^{3} = \frac{500 \sqrt{3}}{27} π .$

Câu 38:

Cho các số thực x,y với $x \geq 0$ thỏa mãn $e^{x + 3 y} + e^{x y + 1} + x (y + 1) + 1 = e^{- x y - 1} + \frac{1}{e^{x + 3 y}} - 3 y .$ Gọi m là giá trị nhỏ nhất của biểu thức $T = x + 2 y + 1.$ Mệnh đề nào sau đây là đúng?

A. $m \in (2; 3) .$

B. $m \in (- 1; 0) .$

C. $m \in (0; 1) .$

D. $m \in (1; 2) .$

Xem đáp án

Chọn C.

+ Ta có $e^{x + 3 y} + e^{x y + 1} + x (y + 1) + 1 = e^{- x y - 1} + \frac{1}{e^{x + 3 y}} - 3 y \Leftrightarrow e^{x + 3 y} - \frac{1}{e^{x + 3 y}} + x + 3 y = e^{- x y - 1} - \frac{1}{e^{- x y - 1}} + (- x y - 1) (*) .$

+ Đặt $f (t) = e^{t} - \frac{1}{e^{t}} + t \Rightarrow f' (t) = e^{t} + \frac{1}{e^{t}} + 1 > 0, \forall t \in ℝ .$ Nên hàm số f(t) đồng biến trên R nên $(*) \Leftrightarrow f (x + 3 y) = f (- x y - 1) .$ Do đó $x + 3 y = - x y - 1 \Leftrightarrow y = - \frac{x + 1}{x + 3} \Rightarrow T = x + 1 - \frac{2 x + 2}{x + 3} = g (x)$

$g' (t) = 1 - \frac{4}{{(x + 3)}^{2}} \geq 0, \forall x \geq 0$ nên g(x) đồng biến trên $[0; + \infty) .$ Suy ra $M i n T = \underset{[0; + \infty)}{M i n} g (x) = g (0) = \frac{1}{3} .$

Câu 39:

Có bao nhiêu giá trị nguyên của tham số m để hàm số $y = |3 x^{4} - 4 x^{3} - 12 x^{2} + m^{2}|$ có đúng 5 điểm cực trị?

A. 5.

B. 7.

C. 6.

D. 4.

Xem đáp án

Chọn B.

Xét hàm số $f (x) = 3 x^{4} - 4 x^{3} - 12 x^{2} + m^{2},$ hàm số đã cho trở thành $y = |f (x)| .$

Tập xác định của f(x) là: R

Ta có $f' (x) = 12 x^{3} - 12 x^{2} - 24 x = 12 x (x^{2} - x - 2), f' (x) = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ x = - 1 \\ x = 2 \end{array} .$

Bảng biến thiên của f(x):

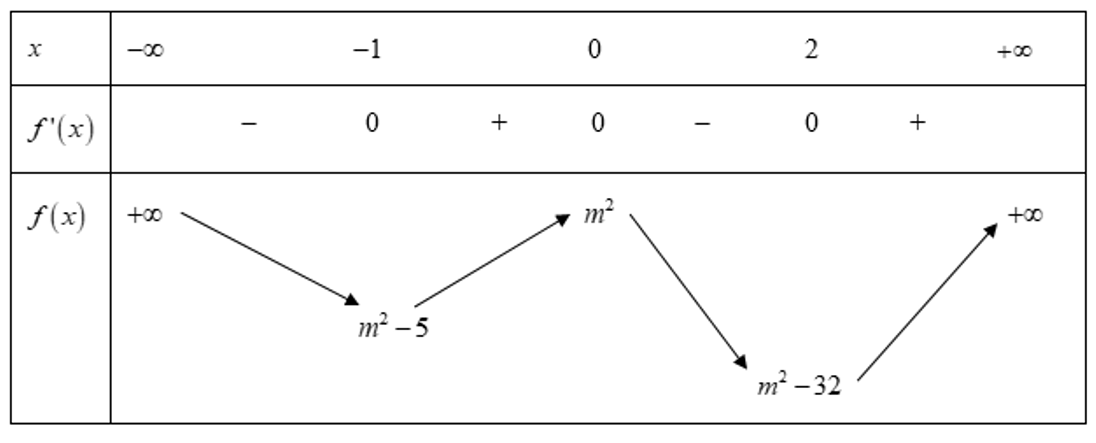
Có bao nhiêu giá trị nguyên của tham số m để hàm số y= |3x^4-4x^3-12x^2+m^2| có đúng 5 điểm cực trị? (ảnh 1)

Số điểm cực trị của đồ thị hàm số $y = |f (x)|$ bằng số cực trị của đồ thị hàm số y= f(x) cộng với số giao điểm của đồ thị y= f(x) với trục hoành (không tính các điểm tiếp xúc).

Từ bảng biến thiên ta được điều kiện để hàm số $y = |f (x)|$ có 5 điểm cực trị là

$[\begin{array}{l} m^{2} - 32 < 0 \leq m^{2} - 5 \\ m^{2} \leq 0 \end{array} \Leftrightarrow [\begin{array}{l} - 4 \sqrt{2} < m \leq - \sqrt{5} \\ \sqrt{5} \leq m < 4 \sqrt{2} \\ m = 0 \end{array}$

Do $m \in ℤ$ nên ta được tập các giá trị của m là $\{- 5; - 4; - 3; 0; 3; 4; 5\} .$

Vậy có 7 giá trị nguyên của m thỏa yêu cầu của bài toán.

Câu 40:

Cho tứ diện SABCD có các cạnh SA,SB,SC đôi một vuông góc với nhau. Biết $S A = 3 a, S B = 4 a, S C = 5 a .$ Tính theo a thể tích V của khối tứ diện S.ABC.

A. $V = 10 a^{3} .$

B. $V = \frac{5 a^{3}}{2} .$

C. $V = 5 a^{3} .$

D. $V = 20 a^{3} .$

Xem đáp án

Chọn A.

Thể tích khối chóp là $V = \frac{1}{3} S A . V_{Δ S B C} = \frac{1}{6} S A . S B . S C = \frac{1}{6} .3 a .4 a .5 a = 10 a^{3} .$

Câu 41:

Cho hình chóp S.ABC có $S A = a, S B = 2 a, S C = 4 a$ và $\hat{A S B} = \hat{B S C} = \hat{C S A} = 60^{0} .$ Tính thể tích khối chóp S.ABC theo a

A. $\frac{a^{3} \sqrt{2}}{3} .$

B. $\frac{8 a^{3} \sqrt{2}}{3} .$

C. $\frac{4 a^{3} \sqrt{2}}{3} .$

D. $\frac{2 a^{3} \sqrt{2}}{3} .$

Xem đáp án

Chọn D.

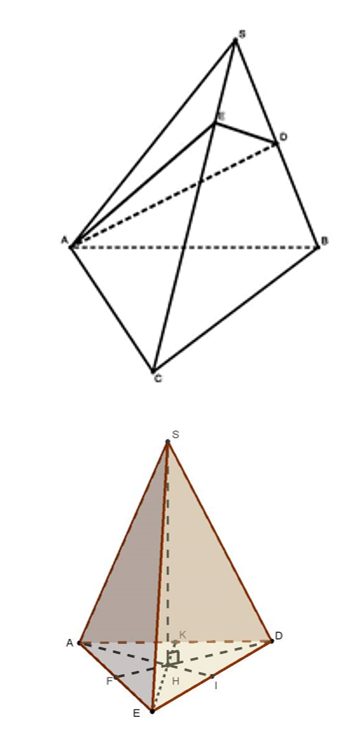
Cho hình chóp S.ABC có SA= a,SB= 2a, SC= 4a và góc ASB= góc BSC= góc CSA= 60 độ (ảnh 1)

Gọi D là trung điểm SB, ta có $S D = \frac{1}{2} A B = a .$

Gọi E là điểm trên cạnh SC sao cho $S E = \frac{1}{4} S C,$ ta có $S E = \frac{1}{4} S C = a .$

Vì $\hat{A S B} = \hat{B S C} = \hat{C S A} = 60^{0}$ và $S A = S E = S D = a$ nên SAED là tứ diện đều cạnh a.

Tứ diện đều SAED có $S_{A D E} = \frac{a^{2} \sqrt{3}}{4}, S H = \sqrt{S E^{2} - E H^{2}} = \sqrt{a^{2} - {(\frac{2}{3} . \frac{a \sqrt{3}}{2})}^{2}} = \frac{a \sqrt{6}}{3} .$

$V_{S A E D} = \frac{1}{3} . S_{A D E} . S H = \frac{1}{3} . \frac{a^{2} \sqrt{3}}{4} . \frac{a \sqrt{6}}{3} = \frac{a^{3} \sqrt{2}}{12} .$

Mặt khác, $\frac{V_{S A E D}}{V_{S . A B C}} = \frac{S D}{S B} . \frac{S E}{S C} = \frac{1}{2} . \frac{1}{4} = \frac{1}{8} .$ Vậy $V_{S . A B C} = 8 V_{S A E D} = 8. \frac{a^{3} \sqrt{2}}{12} = \frac{2 a^{3} \sqrt{2}}{3} .$

Câu 42:

Cần sản xuất một vỏ hộp sữa hình trụ có thể tích V cho trước. Để tiết kiệm vật liệu nhất thì bán kính đáy của vỏ hộp sữa phải bằng

A. $\sqrt[3]{\frac{V}{2 π}} .$

B. $\sqrt[3]{\frac{V}{3 π}} .$

C. $\sqrt[3]{\frac{V}{π}} .$

D. $\sqrt[3]{\frac{V}{2}} .$

Xem đáp án

Chọn A.

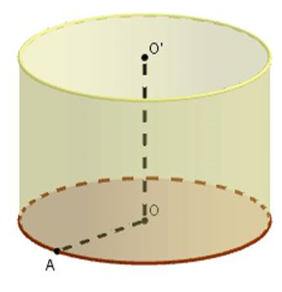
Cần sản xuất một vỏ hộp sữa hình trụ có thể tích V cho trước. Để tiết kiệm vật liệu nhất thì bán (ảnh 1)

Ta có $V = π r^{2} h \Rightarrow h = \frac{V}{π r^{2}} .$

$S_{toaøn phaàn} = S_{xung quanh} + 2 S_{ñaùy} = 2 π r h + 2 π r^{2} = 2 π r . \frac{V}{π r^{2}} + 2 π r^{2} = \frac{2 V}{r} + 2 π r^{2} = \frac{V}{r} + \frac{V}{r} + 2 π r^{2} .$

Áp dụng bất đẳng thức Cauchy cho 3 số dương $\frac{V}{r}, \frac{V}{r}, 2 π r^{2}$ ta có $\frac{V}{r} + \frac{V}{r} + 2 π r^{2} \geq 3 \sqrt[3]{2 π V^{2}} .$

Dấu “=” xảy ra $\Leftrightarrow \frac{V}{r} = 2 π r^{2} \Leftrightarrow r^{3} = \frac{V}{2 π} \Leftrightarrow r = \sqrt[3]{\frac{V}{2 π}} .$

Vậy để tiết kiệm vật liệu nhất thì bán kính đáy của vỏ hộp sữa phải bằng $\sqrt[3]{\frac{V}{2 π}} .$

Câu 43:

Cho hình trụ có diện tích toàn phần là $4 π$ và có thiết diện cắt mặt phẳng qua trục là một hình vuông. Tính thể tích khối trụ.

A. $\frac{4 π}{9} .$

B. $\frac{4 π \sqrt{6}}{9} .$

C. $\frac{π \sqrt{6}}{9} .$

D. $\frac{π \sqrt{6}}{12} .$

Xem đáp án

Chọn B.

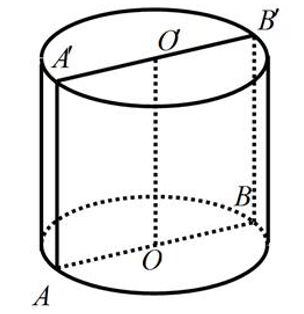
Cho hình trụ có diện tích toàn phần là 4 pi và có thiết diện cắt mặt phẳng qua trục là một (ảnh 1)

Thiết diện qua trục là hình vuông nên $A B = A A' = 2 r \Rightarrow l = 2 r .$

Diện tích toàn phần của khối trụ là:

$S_{T P} = 2 π . r . l + 2 π r^{2} = 2 π . r .2 r + 2 π r^{2} = 6 π r^{2} = 4 π \Rightarrow r = \frac{\sqrt{6}}{3} .$

Nên thể tích khối trụ: $V = B . h = π R^{2} . A A' = π . {(\frac{\sqrt{6}}{3})}^{2} .2. (\frac{\sqrt{6}}{3}) = \frac{4 \sqrt{6}}{9} π .$

Câu 44:

Một hộp đựng thẻ gồm 10 thẻ được đánh số từ 1 đến 10. Rút ngẫu nhiên 2 thẻ từ hộp thẻ đó. Xác suất để 2 thẻ rút được có tổng là một số tự nhiên chia hết cho 3 là

A. $\frac{16}{45} .$

B. $\frac{14}{45} .$

C. $\frac{1}{3} .$

D. $\frac{17}{45} .$

Xem đáp án

Chọn C.

Ta có: $n (Ω) = C_{10}^{2} = 45.$

Gọi A: “2 thẻ rút được có tổng là một số tự nhiên chia hết cho 3”

Từ 1 đến 10 có 3 số tự niên chia hết cho 3 là {3;6;9}

Có 3 số tự nhiên chia hết cho 3 dư 2 là {2;5;8}

Có 4 số tự nhiên chia hết cho 3 dư 1 là {1;4;7;10}

Lấy 2 thẻ rút được có tổng là một số tự nhiên chia hết cho 3 có 2 trường hợp xảy ra:

TH1: 2 số đó chia hết cho 3 nên có $C_{3}^{2} = 3$ cách

TH2: 1 số đó chia cho 3 dư 1 và số còn lại chia 3 dư 2 nên có $C_{3}^{1} . C_{4}^{1} = 3.4 = 12$ cách

$\Rightarrow n (A) = 12 + 3 = 15 \Rightarrow P (A) = \frac{n (A)}{n (Ω)} = \frac{15}{45} = \frac{1}{3} .$

Câu 45:

Cho x, y > 0 thỏa mãn

\log_{6} x = \log_{9} y = \log_{4} (2 x + 2 y) .

Tính

\frac{x}{y} .

A. $\frac{\sqrt{3} - 1}{2} .$

B. $1 + \sqrt{3} .$

C. $\frac{\sqrt{3}}{2} .$

D. $\frac{3}{2} .$

Xem đáp án

Chọn B.

Đặt $\log_{6} x = \log_{9} y = \log_{4} (2 x + 2 y) = t \Rightarrow \{\begin{cases} x = 6^{t} \\ y = 9^{t} \\ 2 x + 2 y = 4^{t} \end{cases}$

$\Rightarrow {2.6}^{t} + {2.9}^{t} = 4^{t} \Leftrightarrow {(\frac{2}{3})}^{2 t} - 2. {(\frac{2}{3})}^{t} - 2 = 0 \Leftrightarrow [\begin{array}{l} {(\frac{2}{3})}^{t} = 1 + \sqrt{3} (n) \\ {(\frac{2}{3})}^{t} = 1 - \sqrt{3} (l) \end{array} \Rightarrow {(\frac{2}{3})}^{t} = 1 + \sqrt{3} .$

Vậy $\frac{x}{y} = 1 + \sqrt{3} .$

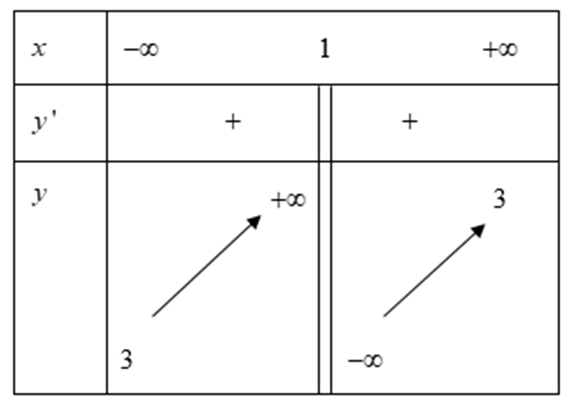
Câu 46:

Đồ thị của hàm số $y = \frac{x - 1}{x^{2} + 2 x - 3}$ có bao nhiêu đường tiệm cận?

A. 0.

B. 2.

C. 3.

D. 1.

Xem đáp án

Chọn B.

Tập xác định: $D = ℝ \ \{- 3; 1\} .$

+) $\{\begin{cases} \lim_{x \to + \infty} y = 0 \\ \lim_{x \to - \infty} y = 0 \end{cases} \Rightarrow$ đường thẳng y = 0 là tiệm cận ngang của đồ thị hàm số đã cho.

+) $\lim_{x \to 1^{+}} y = \lim_{x \to 1^{+}} \frac{1}{x + 3} = \frac{1}{4}$ và $\lim_{x \to 1^{-}} y = \lim_{x \to 1^{-}} \frac{1}{x + 3} = \frac{1}{4}$ nên đường thẳng x= 1 không là đường tiệm cận đứng của đồ thị hàm số đã cho.

+) $\lim_{x \to {(- 3)}^{+}} y = \lim_{x \to {(- 3)}^{+}} \frac{x - 1}{(x - 1) (x + 3)} = + \infty$ và $\lim_{x \to {(- 3)}^{-}} y = \lim_{x \to {(- 3)}^{-}} \frac{x - 1}{(x - 1) (x + 3)} = - \infty$ nên đường thẳng x= -3 là đường tiệm cận đứng của đồ thị hàm số đã cho.

Vậy đồ thị hàm số đã cho có 2 đường tiệm cận.

Câu 47:

Tập xác định của hàm số $y = {(x^{2} - 3 x + 2)}^{\frac{3}{5}} + {(x - 3)}^{- 2}$ là

A. $D = (- \infty; + \infty) \ \{3\} .$

B. $D = (- \infty; + \infty) \ \{1; 2\} .$

C. $D = (- \infty; 1) \cup (2; + \infty) .$

D. $D = (- \infty; 1) \cup (2; + \infty) \ \{3\} .$

Xem đáp án

Chọn D.

Điều kiện xác định: $\{\begin{cases} x^{2} - 3 x + 2 > 0 \\ x - 3 \neq 0 \end{cases} \Leftrightarrow \{\begin{cases} [\begin{array}{l} x < 1 \\ x > 2 \end{array} \\ x \neq 3 \end{cases}$

Tập xác định là $D = (- \infty; 1) \cup (2; + \infty) \ \{3\} .$

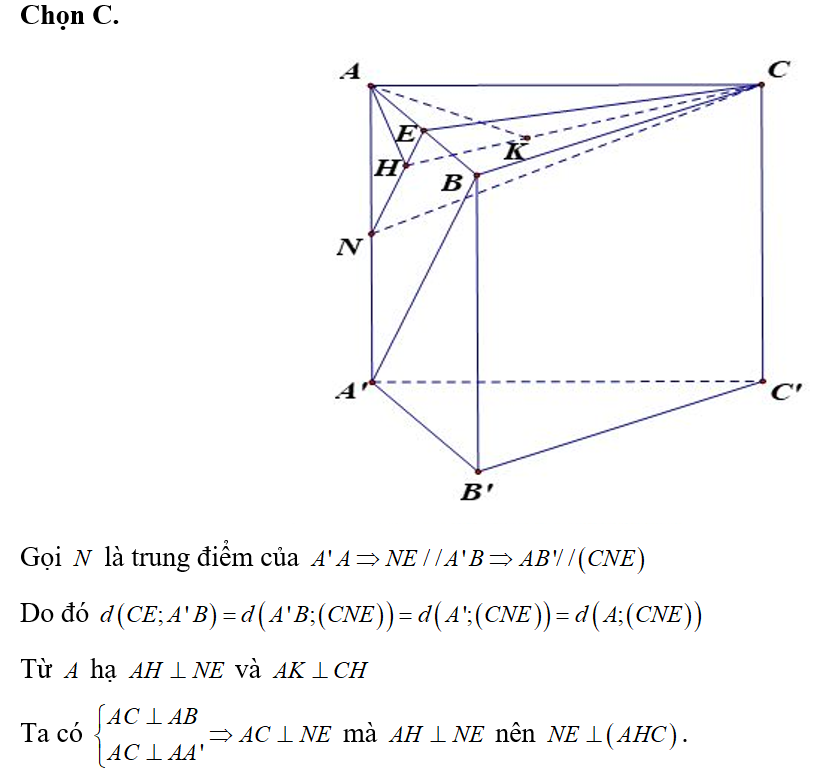
Câu 48:

Cho hình lập phương ABCD.A'B'C'D'. Gọi M và N lần lượt là trung điểm của cạnh AC và B'C'. Góc $α$ là góc hợp giữa đường thẳng MN và mặt phẳng $(A' B' C' D') .$ Tính giá trị của $\sin α .$

A. $\sin α = \frac{\sqrt{5}}{5} .$

B. $\sin α = \frac{2}{\sqrt{5}} .$

C. $\sin α = \frac{\sqrt{2}}{2} .$

D. $\sin α = \frac{1}{2} .$

Xem đáp án

Chọn B.

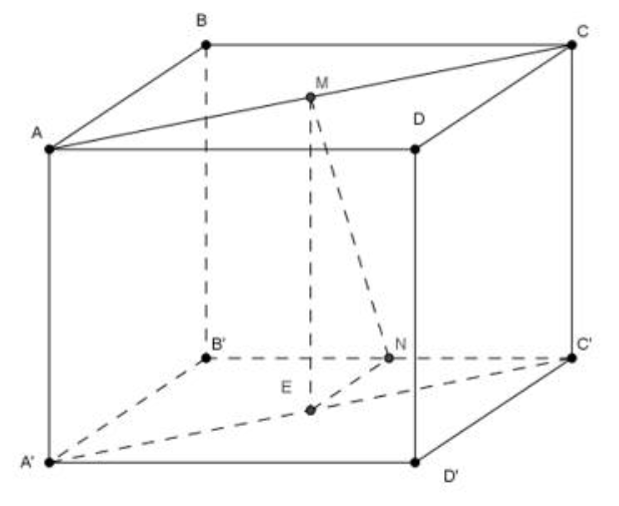
Cho hình lập phương ABCD.A'B'C'D'. Gọi M và N lần lượt là trung điểm của cạnh AC và B'C'. (ảnh 1)

Gọi E là trung điểm A'C' Đặt AB=a

Ta có $M E ⊥ (A' B' C' D'),$ suy ra $\hat{(N M, (A' B' C' D'))} = \hat{M N E} = α$

$M E = a, E N = \frac{a}{2} \Rightarrow N M = \sqrt{a^{2} + \frac{a^{2}}{4}} = \frac{a \sqrt{5}}{2}$

Vậy $\sin α = \frac{M E}{M N} = \frac{a}{\frac{a \sqrt{5}}{2}} = \frac{2}{\sqrt{5}}$ .

Câu 49:

Cho hình lập phương ABCD.A'B'C'D' có đường chéo bằng $a \sqrt{3} .$ Tính thể tích khối chóp A'.ABCD

A. $2 \sqrt{2} a^{3}$

B. $\frac{a^{3}}{3} .$

C. $a^{3}$

D. $\frac{2 \sqrt{2} a^{3}}{3}$

Xem đáp án

Chọn B.

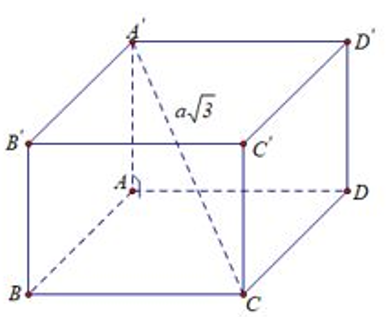
Cho hình lập phương ABCD.A'B'C'D' có đường chéo bằng a căn bậc hai 3. Tính thể tích khối chóp A'.ABCD (ảnh 1)

Độ dài đường chéo $A C' = A B \sqrt{3} = a \sqrt{3} \Rightarrow A B = a .$

Thể tích khối chóp A'.ABCD là $V = \frac{1}{3} . S_{A B C D} . A A' = \frac{a^{3}}{3} .$

Câu 50:

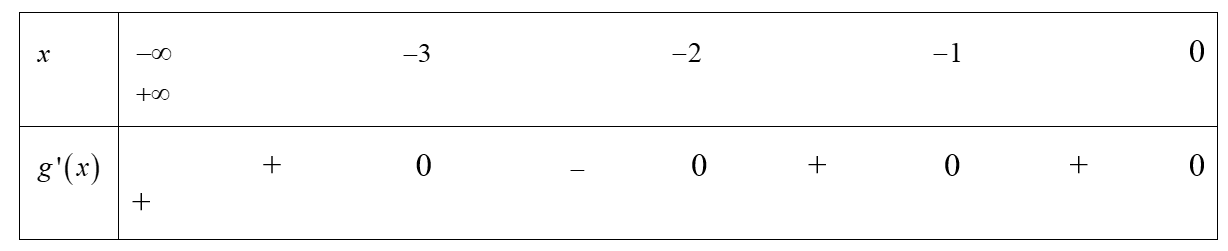
Cho hàm số y= f(x) có đạo hàm trên R. Đồ thị hàm số y = f'(x) như hình vẽ bên dưới.

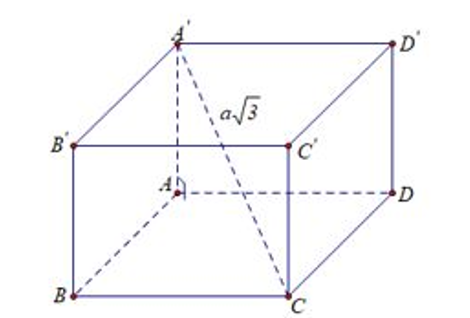
Số điểm cực tiểu của hàm số $g (x) = 2 f (x + 2) + (x + 1) (x + 3)$ là

A. 4.

B. 3.

C. 2.

D. 1.

Xem đáp án

Chọn D.

Ta có : $g (x) = 2 f (x + 2) + x^{2} + 4 x + 3 \Rightarrow g' (x) = 2 f' (x + 2) + 2 x + 4.$

Cho hàm số y= f(x) có đạo hàm trên R. Đồ thị hàm số y = f'(x) như hình vẽ bên dưới. (ảnh 2)

$g' (x) = 0 \Leftrightarrow f' (x + 2) = - x (x + 2)$

$\Leftrightarrow [\begin{array}{l} x + 2 = - 1 \\ x + 2 = 0 \\ x + 2 = 1 \\ x + 2 = 2 \end{array} \Leftrightarrow [\begin{array}{l} x = - 3 \\ x = - 2 \\ x = - 1 \\ x = 0 \end{array} .$

Bảng xét dấu $g' (x)$

Cho hàm số y= f(x) có đạo hàm trên R. Đồ thị hàm số y = f'(x) như hình vẽ bên dưới. (ảnh 3)

Từ bảng xét dấu, suy ra hàm số có một điểm cực tiểu.