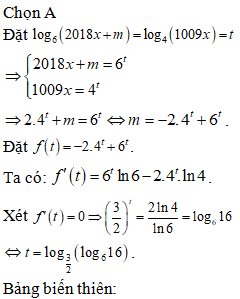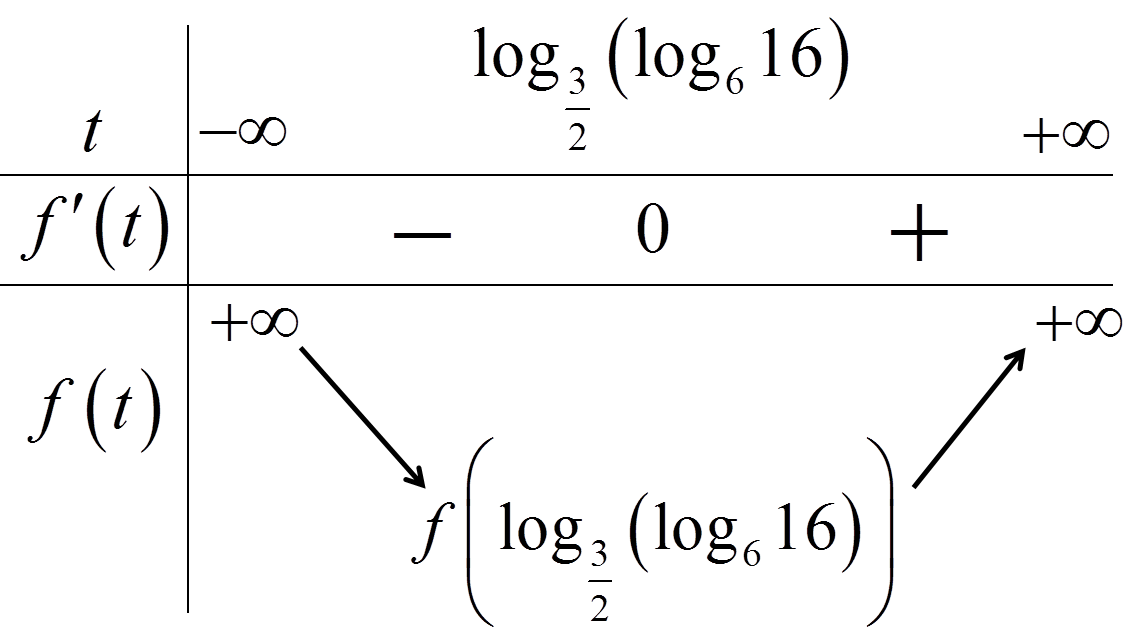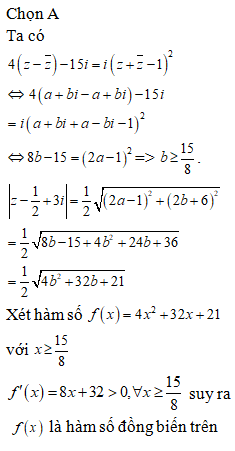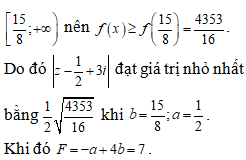50 câu hỏi trắc nghiệm thuộc Đề số 21

Đề minh họa THPT Quốc gia môn Toán năm 2022 chọn lọc, có lời giải (30 đề)

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30

Đề số 21

2263 lượt thi
50 câu hỏi
90 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Có bao nhiêu cách chọn hai học sinh từ một nhóm gồm 10 học sinh?

A. $C_{10}^{2}$

B. $A_{10}^{2}$

C. 10²

D. 2¹⁰

Xem đáp án

Chọn A

Mỗi cách chọn hai học sinh từ một nhóm gồm 10 học sinh tương ứng với một tổ hợp chập 2 của tập có 10 phần tử. Vậy số cách chọn 2 học sinh từ 10 học sinh là $C_{10}^{2}$

Câu 2:

Cho cấp số cộng $(u_{n})$ có $u_{1} = - 2$ và công sai d=3. Tìm số hạng u₁₀.

A. $u_{10} = - {2.3}^{9} .$

B. u₁₀= 25.

C. u₁₀= 28.

D. u₁₀= -29.

Xem đáp án

Câu 3:

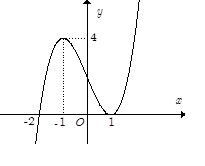
Cho hàm số y=f(x). Biết rằng hàm số f(x) có đạo hàm là f'(x) và hàm số y=f'(x) có đồ thị như hình vẽ bên. Khi đó nhận xét nào sau đây là sai?

Xem đáp án

Chọn B

Dựa vào đồ thị của hàm số y=f'(x) ta thấy:

● f'(x)>0 khi $[\begin{array}{l} - 2 < x < 1 \\ x > 1 \end{array} \Rightarrow$ f(x) đồng biến trên các khoảng (-2;1), $(1; + \infty)$ . Suy ra A và C đều đúng.

● f'(x)<0 khi x<-2 => f(x) nghịch biến trên khoảng $(- \infty; - 2)$ . Suy ra D đúng, B sai.

Câu 4:

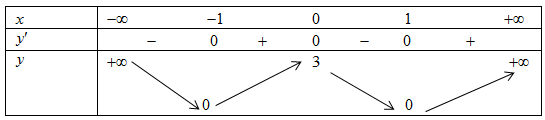
Cho hàm số y=f(x) có bảng biến thiên như sau

Mệnh đề nào dưới đây sai?

A. Hàm số có giá trị cực đại bằng 3.

B. Hàm số có giá trị cực đại bằng 0.

C. Hàm số có 2 điểm cực tiểu.

D. Hàm số có ba điểm cực trị.

Xem đáp án

Chọn B

A. Hàm số có giá trị cực đại bằng 3 (Đúng).

B. Hàm số có giá trị cực đại bằng 0 (Sai vì hàm số có giá trị cực đại bằng 3).

C. Hàm số có 2 điểm cực tiểu (Đúng).

D. Hàm số có ba điểm cực trị (Đúng).

Câu 5:

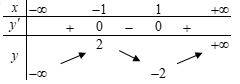
Cho hàm số y=f(x) có bảng biến thiên như hình dưới đây:

Số điểm cực trị của hàm số đã cho bằng

A. -2

B. 1

C. 2

D. -1

Xem đáp án

Chọn C

Theo định nghĩa về cực trị thì hàm số có hai cực trị.

Câu 6:

Tìm đường tiệm cận đứng của đồ thị hàm số

y = \frac{3 - 2 x}{x - 2}

A. x = -2.

B. x = 2.

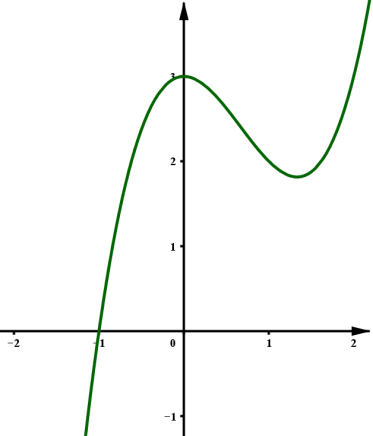
C. y = -2.

D. y = 3.

Xem đáp án

Câu 7:

Đường cong ở hình bên là đồ thị của hàm số nào sau đây

A. $y = x^{3} - 2 x^{2} + 3$ .

B. $y = - x^{3} + 2 x^{2} + 3 .$

C. $y = x^{4} - 3 x^{2} + 3 .$

D. $y = - x^{3} - 2 x^{2} + 3$

Xem đáp án

Chọn A

Đồ thị hàm số có hình dạng của hàm bậc ba nên loại đáp án C.

Hàm số có hệ số a> nên chọn đáp án A.

Câu 8:

Cho hàm số y=f(x) có đồ thị như hình vẽ. Phương trình f(x)-1= có mấy nghiệm?

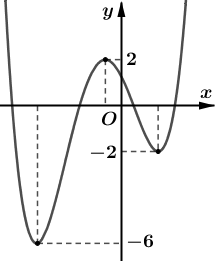
Cho hàm số y=f(x) có đồ thị như hình vẽ. Phương trình (ảnh 1)

A. 2

B. 3

C. 1

D. 4

Xem đáp án

Chọn D

Ta có : f(x) - 1 = 0 => f(x) = 1.

Đồ thị của hàm số y=f(x) cắt đường thẳng y=1 tại bốn điểm phân biệt.

Vậy phương trình f(x) - 1 = 0 có 4 nghiệm

Câu 9:

Cho b là số thực dương tùy ý,

\log_{3^{2}} b

bằng

A. $2 \log_{3} b$ .

B. $\frac{1}{2} \log_{3} b .$

C. $- 2 \log_{3} b .$

D. $- \frac{1}{2} \log_{3} b .$

Xem đáp án

Chọn B

Ta có $\log_{3^{2}} b = \frac{1}{2} \log_{3} b$ .

Câu 10:

Tính đạo hàm của hàm số y = 2017^x?

A. $y^{'} = x {.2017}^{x - 1}$

B. $y^{'} = 2017^{x} \ln 2017$

C. $y^{'} = x {.2017}^{x - 1} . l n 2017$

D. $y^{'} = \frac{2017^{x}}{\ln 2017}$

Xem đáp án

Chọn B

* Áp dụng công thức ${(a^{x})}^{'} = a^{x} . \ln a$ suy ra ${(2017^{x})}^{'} = 2017^{x} . \ln 2017$ .

Câu 11:

Cho a là số thực dương và

a \neq 1

. Giá trị của biểu thức

M = {(a^{1 + \sqrt{2}})}^{1 - \sqrt{2}}

bằng

A. a².

B. $a^{2 \sqrt{2}} .$

C. a.

D. $\frac{1}{a} .$

Xem đáp án

Chọn D

Ta có: $M = {(a^{1 + \sqrt{2}})}^{1 - \sqrt{2}} = a^{1 - 2} = a^{- 1} = \frac{1}{a}$ . Vậy $M = \frac{1}{a}$ .

Câu 12:

Số nghiệm phương trình

3^{x^{2} - 9 x + 8} - 1 = 0

là:

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Chọn C

Ta có: $3^{x^{2} - 9 x + 8} - 1 = 0 \Leftrightarrow 3^{x^{2} - 9 x + 8} = 3^{0} \Leftrightarrow x^{2} - 9 x + 8 = 0$

$\Leftrightarrow [\begin{array}{l} x = 8 \\ x = 1 \end{array}$

Vậy số nghiệm phương trình là 2.

Câu 13:

Nghiệm của phương trình

\log (x^{2} + x + 4) = 1

là

A. {-3;2}.

B. {-3}.

C. {2}.

D. {-2;3}.

Xem đáp án

Câu 14:

Mệnh đề nào sau đây đúng

A. $\int e^{x} d x = e^{x} + C$ .

B. $\int \frac{1}{x} d x = \ln x + C$ .

C. $\int \frac{1}{\cos^{2} x} d x = - \tan x + C$ .

D. $\int \sin x d x = \cos x + C$

Xem đáp án

Chọn A

Từ bảng nguyên hàm cơ bản ta chọn đáp án A.

Câu 15:

Mệnh đề nào sau đây sai?

A. $\int \sin 3 x dx = \frac{1}{3} \cos 3 x + C .$

B. $\int e^{x} dx = e^{x} + C .$

C. $\int x^{3} dx = \frac{x^{4}}{4} + C .$

D. $\int \frac{1}{x} dx = \ln |x| + C .$

Xem đáp án

Chọn A

Ta có: $\int \sin 3 x dx = - \frac{1}{3} \cos 3 x + C$

Do đó mệnh đề A sai.

Câu 16:

Nếu

\int_{1}^{2} f (x) d x = 3, \int_{2}^{5} f (x) d x = - 1

thì

\int_{1}^{5} f (x) d x

bằng

A. 2

B. -2

C. 3

D. 4

Xem đáp án

Chọn A

$\int_{1}^{5} f (x) d x = \int_{1}^{2} f (x) d x + \int_{2}^{5} f (x) d x = 3 - 1 = 2$ .

Câu 17:

Tích phân

I = \int_{0}^{2} (2 x - 1) d x

có giá trị bằng:

A. 1

B. 2

C. 3

D. 0

Xem đáp án

Chọn B

I = \int_{0}^{2} (2 x - 1) d x = {(x^{2} - x)|}_{0}^{2} = 2

Câu 18:

Cho số phức liên hợp của số phức z là

\bar{z} = 1 - 2020 i

khi đó

A. z = 1 + 2020i.

B. z = -1 - 2020i.

C. z = -1 + 2020i.

D. z = 1 - 2020i.

Xem đáp án

Chọn A

Số phức liên hợp của số phức z là $\bar{z} = 1 - 2020 i$ nên z=1+2020i.

Câu 19:

Thu gọn số phức z = i + (2 - 4i) - (3 - 2i) ta được?

A. z = -1-i.

B. z = 1-i.

C. z = -1-2i.

D. z = 1+i.

Xem đáp án

Chọn A

Có: z = -1-i.

Câu 20:

Điểm nào trong hình vẽ dưới đây là điểm biểu diễn số phức liên hợp của z = 2i-3?

A. M.

B. N.

C. P.

D. Q.

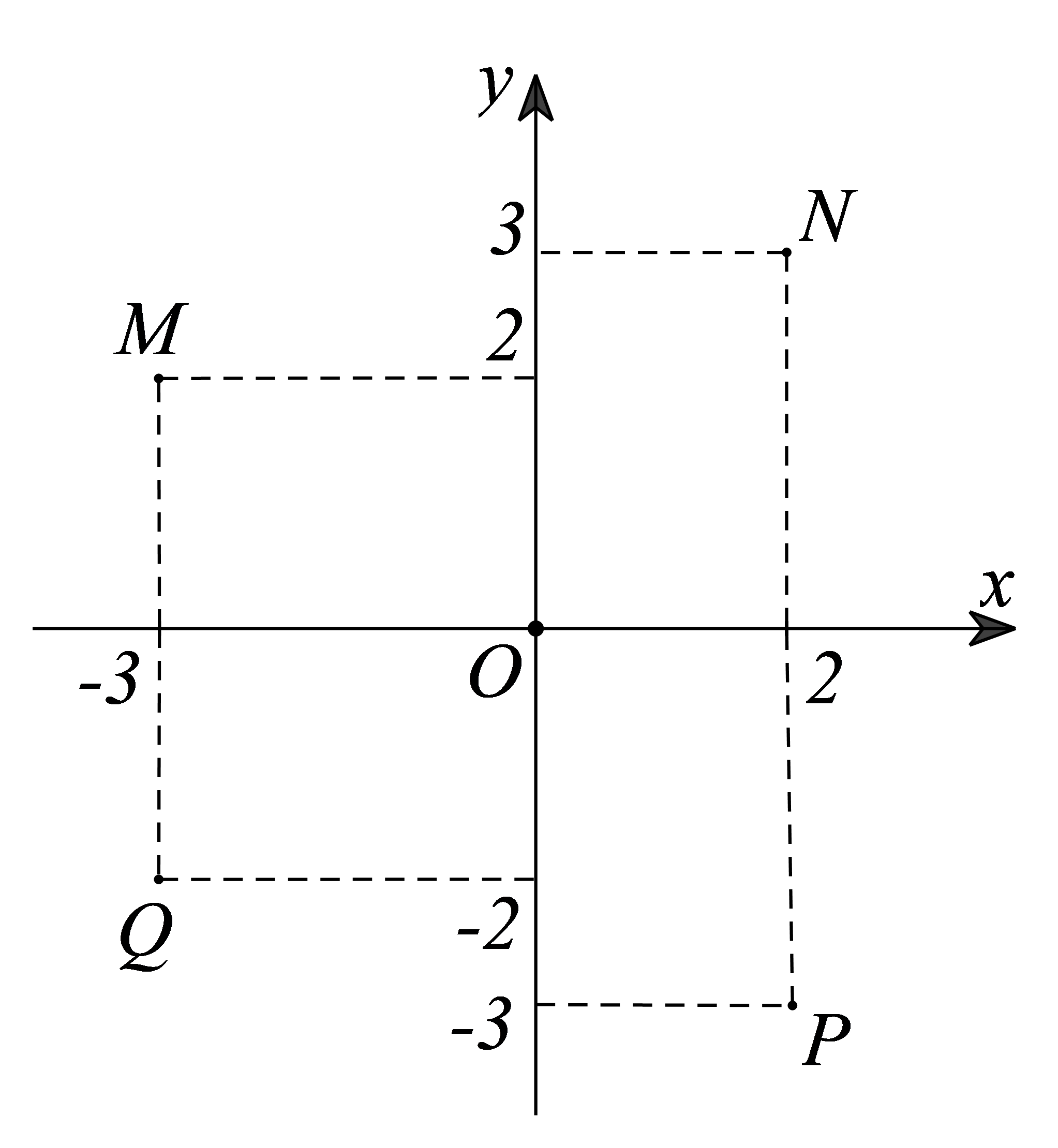
Xem đáp án

Chọn D

Ta có: $z = 2 i - 3 = - 3 + 2 i \Rightarrow \bar{z} = - 3 - 2 i$

=> Điểm biểu diễn của $\bar{z}$ là Q(-3;-2)

Câu 21:

Thể tích của khối lập phương cạnh 2a bằng

A. 6a³

B. 8a³

C. 4a³

D. 2a³

Xem đáp án

Chọn B

$V = {(2 a)}^{3} = 8 a^{3}$ .

Câu 22:

Khối lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông tại A với AB=a, AC=

2 a \sqrt{3}

, cạnh bên AA'=2a. Thể tích khối lăng trụ bằng bao nhiêu?

A. a³

B. $a^{3} \sqrt{3}$

C. $\frac{2 a^{3} \sqrt{3}}{3}$

D. $2 a^{3} \sqrt{3}$

Xem đáp án

Chọn D

Ta có $V = S_{A B C} . A A^{'} = \frac{a .2 a \sqrt{3}}{2} .2 a = 2 a^{3} \sqrt{3}$ .

Câu 23:

Cho khối nón có bán kính đáy r = 2 chiều cao h =

\sqrt{3} .

Thể tích của khối nón

A. $\frac{4 π \sqrt{3}}{3} .$

B. $\frac{4 π}{3} .$

C. $\frac{2 π \sqrt{3}}{3} .$

D. $4 π \sqrt{3} .$

Xem đáp án

Chọn A

Khối nón có thể tích là $V = \frac{1}{3} π r^{2} h = \frac{4 π \sqrt{3}}{3}$

Câu 24:

Cho hình trụ có chiều cao bằng 1 diện tích đáy bằng 3. Tính thể tích khối trụ đó.

A. $3 π .$

B. 3.

C. 1.

D. $π .$

Xem đáp án

Chọn B

Thể tích khối trụ: V=B.h=3.1=3

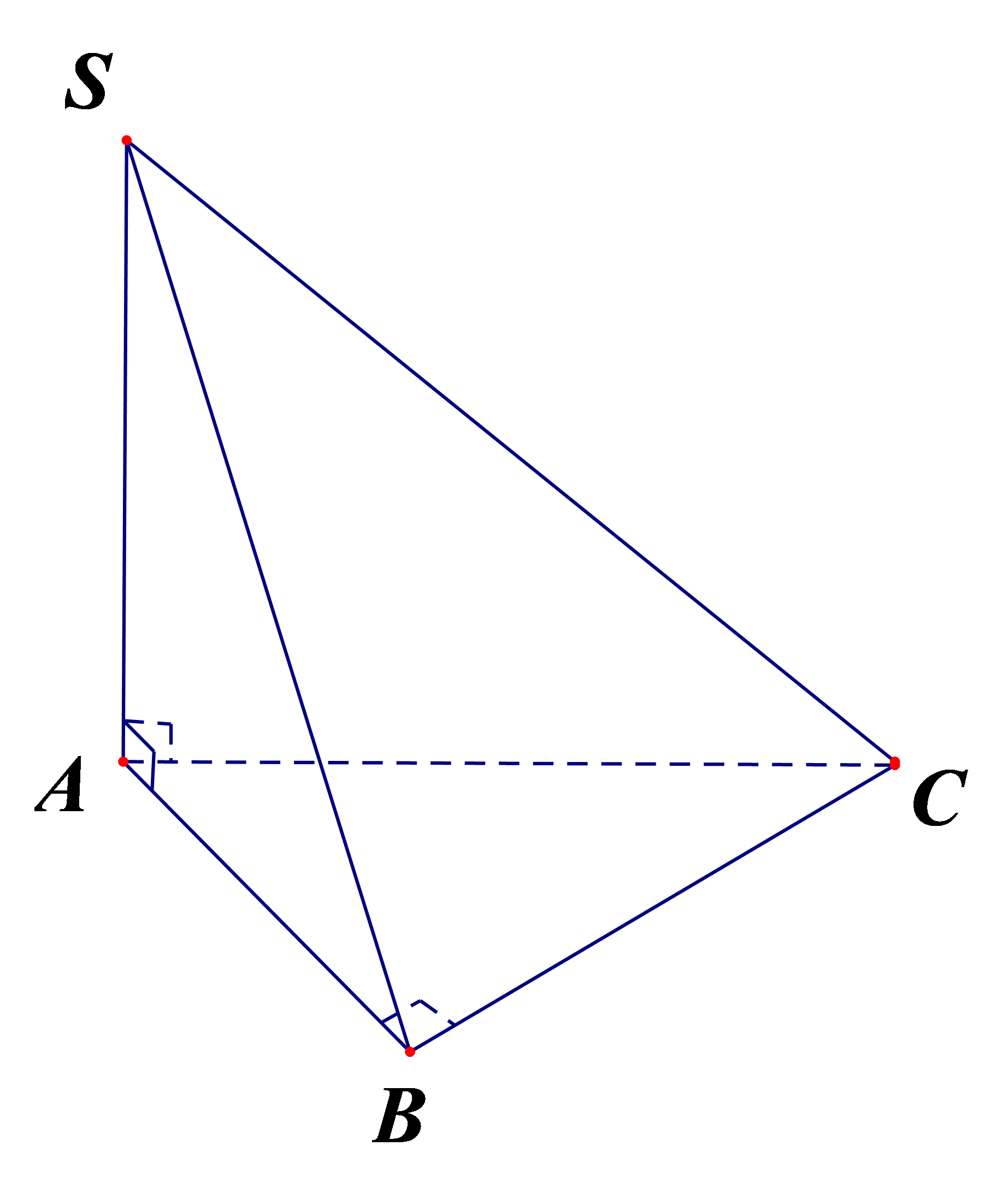
Câu 25:

Trong không gian tọa độ Oxyz, tìm tọa độ điểm H là hình chiếu vuông góc của điểm A(2;1;-10) lên trục tung.

A. H(2;0;-1).

B. H(0;1;0).

C. H(0;1;-1).

D. H(2;0;0).

Xem đáp án

Chọn B

Vì H là hình chiếu của A lên Oy, suy ra $H \in Oy$ nên chỉ có đáp án B thỏa mãn.

Câu 26:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu

(S) : x^{2} + y^{2} + z^{2} - 2 x + 4 y - 4 z - 25 = 0

. Tìm tọa độ tâm I và bán kính mặt cầu (S).

A. $I (1; - 2; 2); R = \sqrt{34}$

B. $I (- 1; 2; - 2); R = 5$

C. $I (- 2; 4; - 4); R = \sqrt{29}$

D. $I (1; - 2; 2); R = 6$

Xem đáp án

Chọn A

Mặt cầu (S) có tâm $I (1; - 2; 2); R = \sqrt{1^{2} + {(- 2)}^{2} + 2^{2} + 25} = \sqrt{34}$ .

Vậy, ta chọn A.

Câu 27:

Trong không gian với hệ tọa độ Oxyz cho hai mặt phẳng

(P) : x - m^{2} y + 2 z + m - \frac{3}{2} = 0

;

(Q) : 2 x - 8 y + 4 z + 1 = 0

, với m là tham số thực. Tìm tất cả các giá trị của tham số m sao cho hai mặt phẳng trên song song với nhau.

A. $m = \pm 2$ .

B. Không tồn tại m.

C. m = 2.

D. m = -2.

Xem đáp án

Chọn D

Hướng dẫn: để (P)//(Q) thì $\frac{1}{2} = \frac{- m^{2}}{- 8} = \frac{2}{4} \neq \frac{m - \frac{3}{2}}{1}$ $\Leftrightarrow \{\begin{cases} m = \pm 2 \\ 4 m - 6 \neq 2 \end{cases} \Leftrightarrow m = - 2$ .

Câu 28:

Cho hai điểm A(4;1;0), B(2;-1;2). Trong các vectơ sau, tìm một vectơ chỉ phương của đường thẳng AB.

A. $\vec{u} = (1; 1; - 1)$

B. $\vec{u} = (3; 0; - 1)$

C. $\vec{u} = (6; 0; 2)$

D. $\vec{u} = (2; 2; 0)$

Xem đáp án

Chọn A

Ta có $\vec{A B} = (- 2; - 2; 2)$ $\Rightarrow \vec{u} = (1; 1; - 1)$ .

Câu 29:

Rút ra một lá bài từ bộ bài 52 lá. Xác suất để được lá bích là:

A. $\frac{1}{13}$

B. $\frac{1}{4}$

C. $\frac{12}{13}$

D. $\frac{3}{4}$

Xem đáp án

Chọn B

Số phần tử không gian mẫu: $n (Ω) = 52$

Số phần tử của biến cố xuất hiện lá bích: n(A)=13

Suy ra $P (A) = \frac{n (A)}{n (Ω)} = \frac{13}{52} = \frac{1}{4}$ .

Câu 30:

Cho hàm số

y = \frac{1}{3} x^{3} - \frac{1}{2} x^{2} - 12 x - 1

. Mệnh đề nào sau đây đúng?

A. Hàm số nghịch biến trên khoảng $(- \infty; 4$ ).

B. Hàm số đồng biến trên khoảng (-3;4).

C. Hàm số nghịch biến trên khoảng

(- 3; + \infty)

D. Hàm số đồng biến trên khoảng

(4; + \infty)

Xem đáp án

Chọn D

Tập xác định: D=R.

Ta có $y^{'} = x^{2} - x - 12. y^{'} = 0 \Leftrightarrow x^{2} - x - 12 = 0 \Leftrightarrow [\begin{array}{l} x = - 3 \\ x = 4 \end{array} .$

Bảng biến thiên

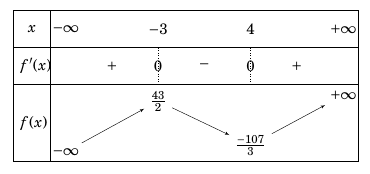
Dựa vào bảng biến thiên: Hàm số đồng biến trên khoảng $(4; + \infty)$ .

Câu 31:

Gọi M,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số

y = \frac{x + 2}{x - 1}

trên đoạn [2;3] . Tính

M^{2} + m^{2}

A. 16

B. $\frac{45}{4}$

C. $\frac{25}{4}$

D. $\frac{89}{4}$

Xem đáp án

Câu 32:

Tập nghiệm của bất phương trình ln(1-x)<0

A. $(- \infty; 1)$

B. (0;1)

C. $(0; + \infty)$

D. $(- \infty; 0)$

Xem đáp án

Chọn B

Ta có: $\ln (1 - x) < 0 \Leftrightarrow 0 < 1 - x < e^{0} \Leftrightarrow 0 < x < 1$ .

Câu 33:

Cho hàm số f(x) liên tục trên R và thỏa mãn

\int_{- 5}^{1} f (x) d x = 9

. Tính tích phân

\int_{0}^{2} [f (1 - 3 x) + 9] d x

A. 27

B. 21

C. 15

D. 75

Xem đáp án

Câu 34:

Cho hai số phức

z_{1} = 4 - 3 i + {(1 - i)}^{3}

và

z_{2} = 7 + i

. Phần thực của số phức

w = 2 \bar{\bar{z_{1}} z_{2}}

bằng

A. 9

B. 2

C. 18

D. -74

Xem đáp án

Chọn C

Ta có $z_{1} = 4 - 3 i + (1 - 3 i + 3 i^{2} - i^{3}) = 4 - 3 i + (1 - 3 i - 3 + i) = 2 - 5 i$ .

Suy ra ${\bar{z}}_{1} . z_{2} = (2 + 5 i) (7 + i) = 9 + 37 i \Rightarrow \bar{\bar{z_{1}} . z_{2}} = 9 - 37 i .$

Do đó $w = 2 (9 - 37 i) = 18 - 74 i$ .

Vậy phần thực của số phức $w = 2 \bar{\bar{z_{1}} z_{2}}$ bằng 18.

Câu 35:

Cho hình chóp S.ABC có SA vuông góc với ABC. Tam giác ABC là vuông cân tại B. Độ dài các cạnh SA=AB=a. Khi đó góc giữa SA và mặt phẳng (SBC)bằng

A. $60 °$

B. $30 °$

C. $90 °$

D. $45 °$

Xem đáp án

Câu 36:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và SA=a. Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng:

A. $a \sqrt{2} .$

B. $\frac{a}{2}$

C. $\frac{a \sqrt{2}}{2}$

D. $\frac{a \sqrt{3}}{2}$

Xem đáp án

Câu 37:

Trong không gian với hệ tọa độ Oxyz cho mặt cầu (S) có tâm I(-1;4;2) và bán kính R=9. Phương trình của mặt cầu (S) là:

A. ${(x + 1)}^{2} + {(y - 4)}^{2} + {(z - 2)}^{2} = 81.$

B. ${(x + 1)}^{2} + {(y - 4)}^{2} + {(z - 2)}^{2} = 9.$

C. ${(x - 1)}^{2} + {(y + 4)}^{2} + {(z - 2)}^{2} = 9.$

D. ${(x - 1)}^{2} + {(y + 4)}^{2} + {(z + 2)}^{2} = 81.$

Xem đáp án

Chọn A

Mặt cầu (S) có tâm I(-1;4;2) và bán kính R=9 nên (S) có phương trình ${(x + 1)}^{2} + {(y - 4)}^{2} + {(z - 2)}^{2} = 81$ .

Câu 38:

Trong không gian Oxyz, đường thẳng đi qua hai điểm M(-1;0;0) và N(0;1;2) có phương trình

A. $\frac{x}{1} = \frac{y + 1}{1} = \frac{z - 2}{2}$

B. $\frac{x - 1}{1} = \frac{y}{1} = \frac{z}{2}$

C. $\frac{x}{1} = \frac{y - 1}{1} = \frac{z + 2}{2}$

D. $\frac{x + 1}{1} = \frac{y}{1} = \frac{z}{2}$

Xem đáp án

Chọn D

Đường thẳng đi qua hai điểm M(-1;0;0) và N(0;1;2) có một véctơ chỉ phương là $\vec{M N} = (1; 1; 2)$ do đó nó có phương trình chính tắc là $\frac{x + 1}{1} = \frac{y}{1} = \frac{z}{2}$ .

Câu 39:

Hàm số y=f(x) có đồ thị y=f'(x) như hình vẽ.

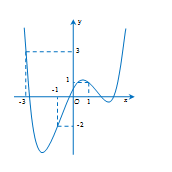
Xét hàm số $g (x) = f (x) - \frac{1}{3} x^{3} - \frac{3}{4} x^{2} + \frac{3}{2} x + 2017$

Trong các mệnh đề dưới đây

(I) g(0)<g(1).

(II) $\min_{x \in [- 3; 1]} g (x) = g (- 1)$ .

(III) Hàm số g(x)nghịch biến trên (-3;-1).

(IV) $\max_{x \in [- 3; 1]} g (x) = \max \{g (- 3), g (1)\}$ .

Số mệnh đề đúng là

A. 2

B. 1

C. 3

D. 4

Xem đáp án

Chọn D

Ta có $g' (x) = f' (x) - x^{2} - \frac{3}{2} x + \frac{3}{2} = f' (x) - (x^{2} + \frac{3}{2} x - \frac{3}{2})$ . Căn cứ vào đồ thị ta có: $\{\begin{cases} f' (- 1) = - 2 \\ f' (1) = 1 \\ f' (- 3) = 3 \end{cases} \Rightarrow \{\begin{cases} g' (- 1) = 0 \\ g' (1) = 0 \\ g' (- 3) = 0 \end{cases}$

Vẽ Parabol (P): $y = x^{2} + \frac{3}{2} x - \frac{3}{2}$ trên cùng hệ trục với đồ thị của hàm số y=f'(x)

Ta có: Trên (-3;-1) thì $f' (x) < x^{2} + \frac{3}{2} x - \frac{3}{2}$ nên $g' (x) < 0 \forall x \in (- 3; - 1)$

Trên (-1;1) thì $f' (x) > x^{2} + \frac{3}{2} x - \frac{3}{2}$ nên $g' (x) > 0 \forall x \in (- 1; - 1)$

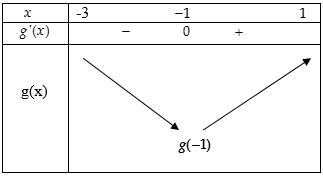
Khi đó BBT của hàm số g(x) trên đoạn [-3;1]:

Vậy $\min_{x \in [- 3; 1]} g (x) = g (- 1)$ , g(0)<g(1), hàm số g(x) nghịch biến trên (-3;-1) và $\max_{x \in [- 3; 1]} g (x) = \max \{g (- 3), g (- 1)\}$ .

Câu 40:

Tất cả các giá trị của tham số m để bất phương trình

{(\sqrt{10} + 1)}^{x} - m {(\sqrt{10} - 1)}^{x} > 3^{x + 1}

nghiệm đúng với mọi

x \in ℝ

là :

A. $m < - \frac{7}{4}$

B. $m < - \frac{9}{4}$

C. m < -2

D. $m < - \frac{11}{4}$

Xem đáp án

Câu 41:

Giả sử hàm số y=f(x) liên tục, nhận giá trị dương trên

(0; + \infty)

và thỏa mãn f(1)=e,

f (x) = f^{'} (x) . \sqrt{3 x + 1},

với mọi x>0. Mệnh đề nào sau đây là đúng?

A. 10 < f(5) < 11.

B. 4 < f(5) < 5.

C. 11 < f(5) < 12.

D. 3 < f(5) < 4.

Xem đáp án

Câu 42:

Có bao nhiêu số phức z = x + yi thỏa mãn hai điều kiện |z + 1 - i| + 10 = |z| và $\frac{x}{y} = - \frac{1}{2}$ .

A. 0

B. 2

C. 1

D. 3

Xem đáp án

Câu 43:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng (ABCD); góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng $60 °$ . Tính theo a thể tích khối chóp S.ABCD.

A. 3a³

B. $\frac{a^{3} \sqrt{6}}{9}$

C. $\frac{a^{3} \sqrt{6}}{3}$

D. $3 \sqrt{2} a^{3}$

Xem đáp án

Câu 44:

Một mảnh vườn hình tròn tâm O bán kính 6m. Người ta cần trồng cây trên dải đất rộng 6m nhận O làm tâm đối xứng, biết kinh phí trồng cây là 70000 đồng/m². Hỏi cần bao nhiêu tiền để trồng cây trên dải đất đó (số tiền được làm tròn đến hàng đơn vị).

A. 4821232 đồng.

B. 8412322 đồng.

C. 8142232 đồng.

D. 4821322 đồng.

Xem đáp án

Câu 45:

Trong không gian với hệ toạ độ Oxyz, cho điểm M(1;-3;4), đường thẳng d: $\frac{x + 2}{3} = \frac{y - 5}{- 5} = \frac{z - 2}{- 1}$ và mặt phẳng (P): 2x+z-2=0. Viết phương trình đường thẳng qua M vuông góc với d và song song với (P).

A. $\frac{x - 1}{1} = \frac{y + 3}{- 1} = \frac{z - 4}{- 2}$

B. $\frac{x - 1}{- 1} = \frac{y + 3}{- 1} = \frac{z - 4}{- 2}$

C. $\frac{x - 1}{1} = \frac{y + 3}{1} = \frac{z - 4}{- 2}$

D. $\frac{x - 1}{1} = \frac{y + 3}{- 1} = \frac{z + 4}{2}$

Xem đáp án

Câu 46:

Cho hàm số y=f(x) có bảng biến thiên như sau

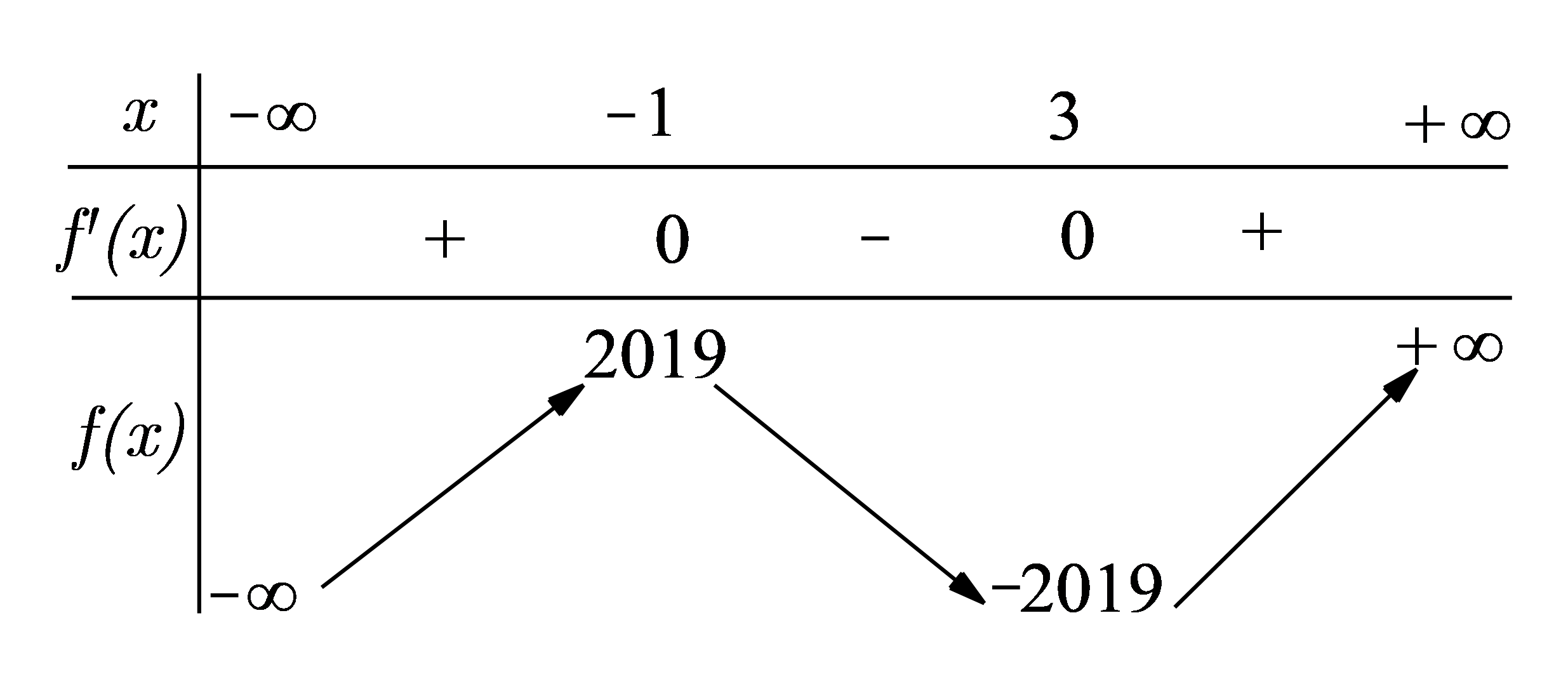Đồ thị hàm số y=|f(x-2018)+2019| có bao nhiêu điểm cực trị?

A. 5

B. 4

C. 2

D. 3

Xem đáp án

Chọn D

Xét hàm số g(x) = f(x-2018)+2019

$g^{'} (x) = {(x - 2018)}^{'} f^{'} (x - 2018) = f^{'} (x - 2018)$

$g^{'} (x) = 0 \Leftrightarrow [\begin{array}{l} x - 2018 = - 1 \\ x - 2018 = 3 \end{array} \Leftrightarrow [\begin{array}{l} x = 2017 \\ x = 2021 \end{array}$

Ta có $g (2017) = f (2017 - 2018) + 2019 = 4038$ ;

$g (2021) = f (2021 - 2018) + 2019 = 0$ ;

Bảng biến thiên hàm g(x)

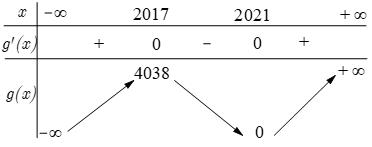
Khi đó bảng biến thiên |g(x)| là

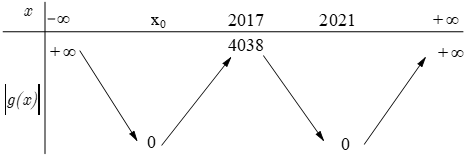
Vậy hàm số y=|f(x-2018)+2019| có ba điểm cực trị.

Câu 47:

Số các giá trị nguyên nhỏ hơn 2018 của tham số m để phương trình

\log_{6} (2018 x + m) = \log_{4} (1009 x)

có nghiệm là

A. 2020

B. 2017

C. 2019

D. 2018

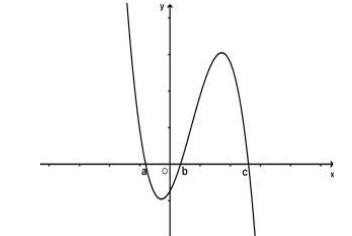
Xem đáp án

Câu 48:

Cho hàm số y=f(x) có đồ thị y=f'(x) cắt trục Ox tại ba điểm có hoành độ a<b<c như hình vẽ. Mệnh đề nào dưới đây là đúng?

Cho hàm số y=f(x) có đồ thị y=f'(x) cắt trục Ox tại ba điểm có hoành độ a<b<c (ảnh 1)

A. f(c) > f(a) > f(b).

B. f(c) > f(b) > f(a).

C. f(a) > f(b) > f(c).

D. f(b) > f(a) > f(c).

Xem đáp án

Chọn A

Từ đồ thị của hàm số y=f'(x), ta có bảng biến thiên của hàm số y=f(x) như sau:

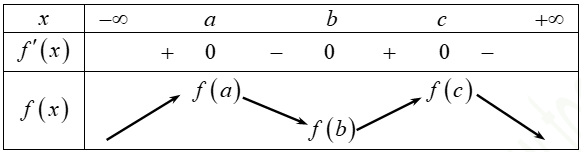
Từ đó suy ra f(a) > f(b), f(c) > f(b). (1)

Mặt khác, từ đồ thị hàm số y=f'(x) ta cũng có: $\int_{b}^{c} f^{'} (x) d x > - \int_{a}^{b} f^{'} (x) d x \Leftrightarrow f (c) - f (b) > - f (b) + f (a) \Leftrightarrow f (c) > f (a)$ . (2)

Từ (1) và (2) suy ra f(c)>f(a)>f(b).

Câu 49:

Xét các số phức z=a+bi,

(a, b \in ℝ)

thỏa mãn

4 (z - \bar{z}) - 15 i = i {(z + \bar{z} - 1)}^{2}

. Tính

F = - a + 4 b

khi

|z - \frac{1}{2} + 3 i|

đạt giá trị nhỏ nhất

A. F = 7

B. F = 6

C. F = 5

D. F = 4

Xem đáp án

Câu 50:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu

(S) : {(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2} = 16

. Gọi M là điểm thuộc mặt cầu (S) sao cho biểu thức

A = 2 x_{M} - y_{M} + 2 z_{M}

đạt giá trị lớn nhất, giá trị biểu thức

B = x_{M} + y_{M} + z_{M}

bằng.

A. 21

B. 3

C. 5

D. 10

Xem đáp án

Chọn D

Ta có: $A = 2 x_{M} - y_{M} + 2 z_{M} = 2 (x_{M} - 1) - (y_{M} - 2) + 2 (z_{M} - 3) + 6$

$\leq \sqrt{(2^{2} + 1^{2} + 2^{2}) ({(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2})} + 6 = 3.4 + 6 = 18$ .

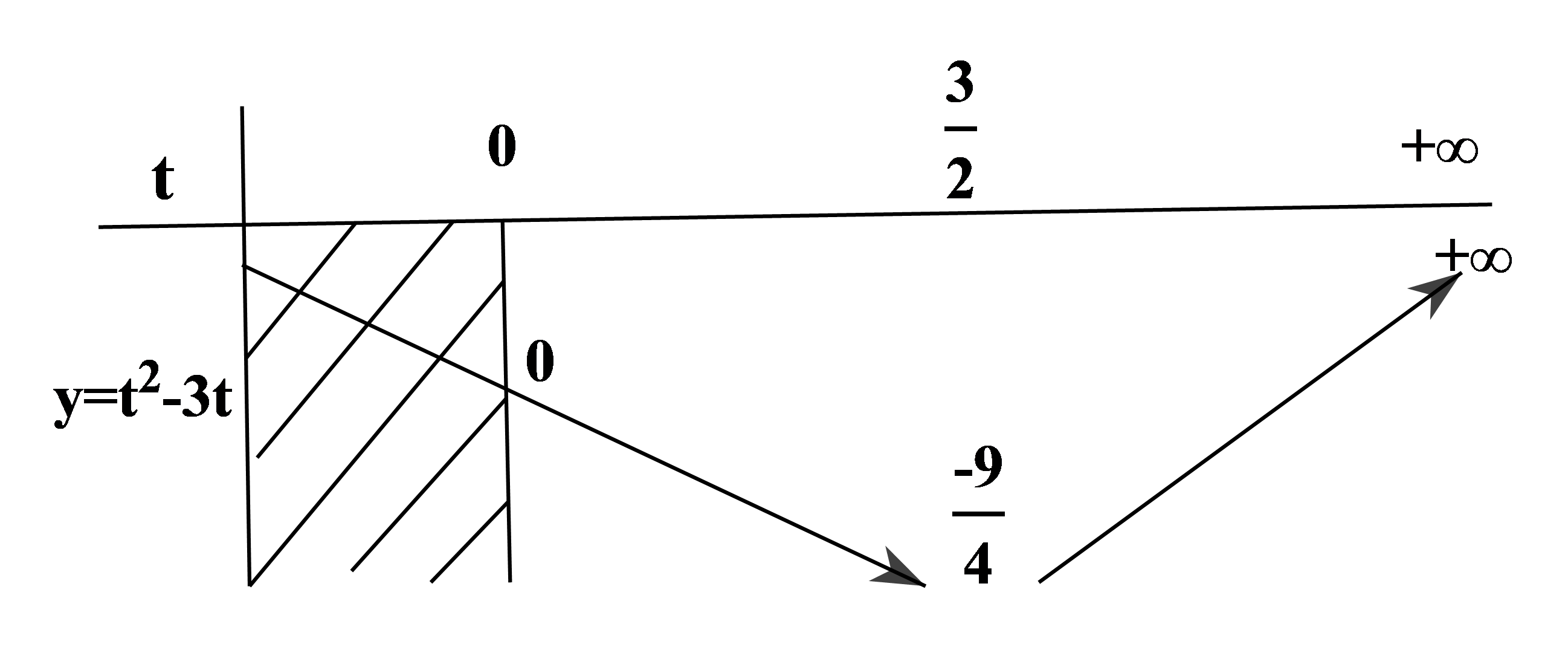
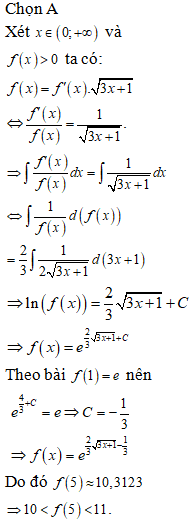
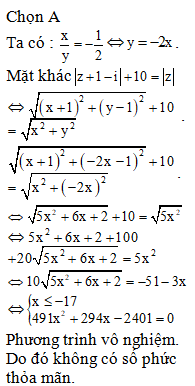
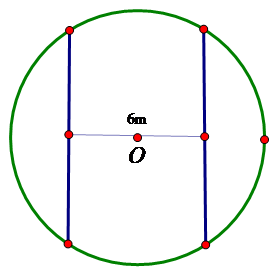Dấu bằng xảy ra khi $\frac{x_{M} - 1}{2} = \frac{y_{M} - 2}{- 1} = \frac{z_{M} - 3}{2} = t > 0 \Rightarrow \{\begin{cases} x_{M} = 1 + 2 t \\ y_{M} = 2 - t \\ Z_{M} = 3 + 2 t \end{cases}$ , thay vào phương trình (S) ta được: $4 t^{2} + t^{2} + 4 t^{2} = 16 \Rightarrow t = \frac{4}{3}$ . Do đó $M (\frac{11}{3}; \frac{2}{3}; \frac{17}{3})$ và $B = x_{M} + y_{M} + z_{M} = 10$ .

Bắt đầu thi ngay

Bài thi liên quan

Đề số 1
- 33 câu hỏi
- 90 phút
Đề số 2
- 53 câu hỏi
- 90 phút
Đề số 3
- 50 câu hỏi
- 90 phút
Đề số 4
- 50 câu hỏi
- 90 phút
Đề số 5
- 50 câu hỏi
- 90 phút
Đề số 6
- 50 câu hỏi
- 90 phút
Đề số 7
- 50 câu hỏi
- 90 phút
Đề số 8
- 50 câu hỏi
- 90 phút
Đề số 9
- 50 câu hỏi
- 90 phút
Đề số 10
- 50 câu hỏi
- 90 phút