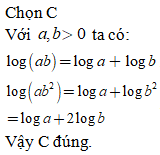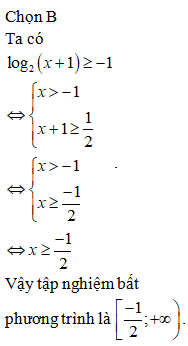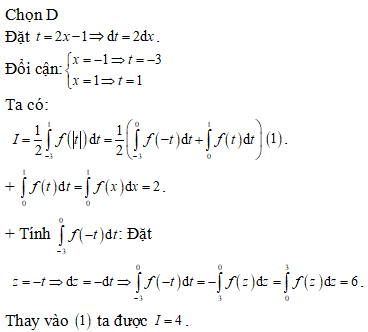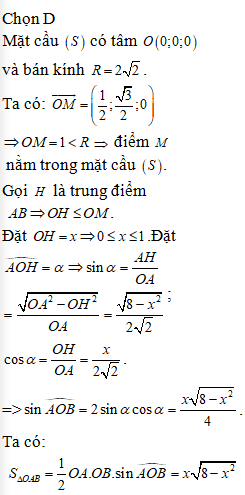50 câu hỏi trắc nghiệm thuộc Đề số 23

Đề minh họa THPT Quốc gia môn Toán năm 2022 chọn lọc, có lời giải (30 đề)

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30

Đề số 23

2382 lượt thi
50 câu hỏi
90 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cần chọn 3 người đi công tác từ một tổ có 30 người, khi đó số cách chọn là:

A. $A_{30}^{3}$

B. 3³⁰

C. 10

D. $C_{30}^{3}$

Xem đáp án

Chọn D

Mỗi cách chọn thỏa đề bài là một tổ hợp chập 3 của 30

Do đó số cách chọn là $C_{30}^{3}$ cách

Câu 2:

Một cấp số cộng có 8 số hạng. Số hạng đầu là 5, số hạng thứ tám là 40. Khi đó công sai d của cấp số cộng đó là bao nhiêu?

A. d = 4.

B. d = 5.

C. d = 6.

D. d = 7.

Xem đáp án

Chọn B

$\{\begin{cases} u_{1} = 5 \\ 40 = u_{8} = u_{1} + 7 d \end{cases} \underset{}{\to} d = 5$

Vậy d = 5.

Câu 3:

Cho hàm số có bảng biến thiên như hình bên dưới.Mệnh đề nào sau đây đúng?

A. Hàm số đồng biến trên khoảng (0; $+ \infty) .$

B. Hàm số nghịch biến trên khoảng (-1;1).

C. Hàm số đồng biến trên khoảng (-1;0).

D. Hàm số nghịch biến trên khoảng (0;1).

Xem đáp án

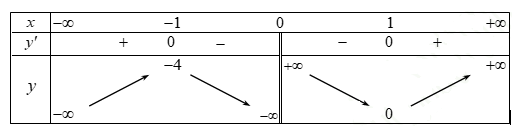
Chọn D

Dựa vào bảng biến thiên ta có:

Hàm số đã cho nghịch biến trên khoảng (0;1) .

Chú ý: Đáp án B sai vì hàm số không xác định tại x=0.

Câu 4:

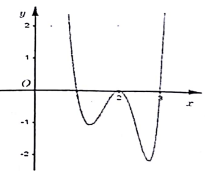
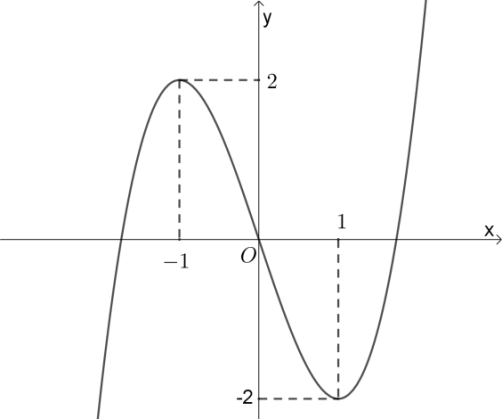
Cho hàm số y=f(x) có đồ thị

Hàm số đã cho đạt cực đại tại

A. x = -1.

B. x = 2.

C. x = 1.

D. x = -2.

Xem đáp án

Chọn A

Từ đồ thị hàm số suy ra hàm số đạt cực đại tại x = -1.

Câu 5:

Cho hàm số y=f(x) có đồ thị trên một khoảng K như hình vẽ bên. Trên K, hàm số có bao nhiêu cực trị?

A. 3

B. 2

C. 0

D. 1

Xem đáp án

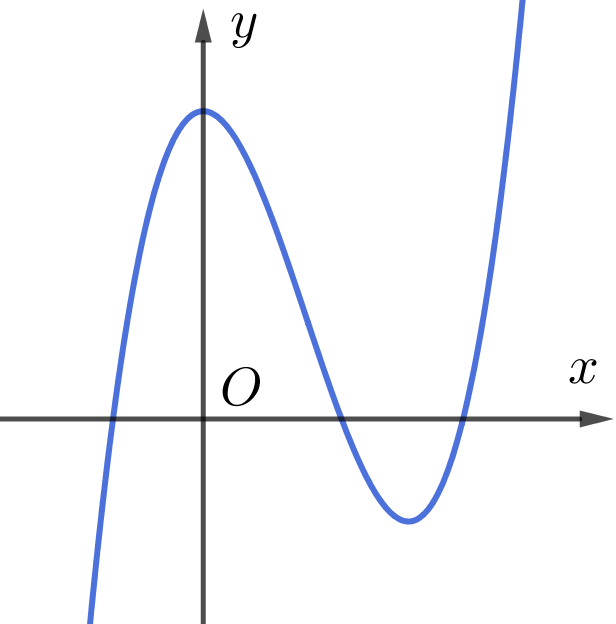
Chọn B

Trên K, hàm số có 2 cực trị.

Câu 6:

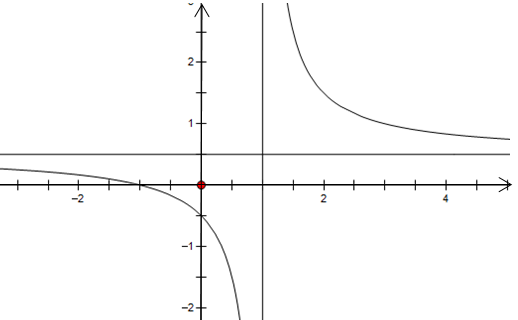
Đường tiệm cận ngang của đồ thị hàm số $y = \frac{2 x - 4}{x + 2}$ là

A. x = 2.

B. y = 2.

C. x = -2.

D. y = -2.

Xem đáp án

Chọn B

Ta có: $\lim_{x \to + \infty} \frac{2 x - 4}{x + 2} = \lim_{x \to - \infty} \frac{2 x - 4}{x + 2}$ .

Vậy y=2 là tiệm cận ngang của đồ thị hàm số đã cho.

Câu 7:

Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?

A. $y = \frac{x + 2}{2 x - 1}$

B. $y = \frac{2 x}{3 x - 3}$

C. $y = \frac{x + 1}{2 x - 2}$

D. $y = \frac{2 x - 4}{x - 1}$

Xem đáp án

Câu 8:

Tìm tung độ giao điểm của đồ thị

(C) : y = \frac{2 x - 3}{x + 3}

và đường thẳng d: y=x-1.

A. 1

B. -3

C. -1

D. 3

Xem đáp án

Chọn C

Phương trình hoành độ giao điểm của hai đường (C) và d là: $\frac{2 x - 3}{x + 3} = x - 1 (x \neq - 3) \Rightarrow x^{2} = 0 \Leftrightarrow x = 0 \Rightarrow y = - 1.$

Câu 9:

Với a,b>0 tùy ý, mệnh đề nào dưới đây đúng?

A. log(ab)=loga.logb

B. log(ab²)=2loga+2logb

C. log(ab²)=loga+2logb

D. log(ab)=loga-logb

Xem đáp án

Câu 10:

Đạo hàm của hàm số y = 5^x + 2017 là:

A. $y' = \frac{5^{x}}{5 \ln 5}$

B. $y' = 5^{x} . \ln 5$

C. $y' = \frac{5^{x}}{\ln 5}$

D. $y' = 5^{x}$

Xem đáp án

Chọn B

Do $(5^{x})' = 5^{x} . \ln 5$ là mệnh đề đúng.

Câu 11:

Cho a là số thực dương. Giá trị của biểu thức

P = a^{\frac{2}{3}} \sqrt{a}

bằng

A. $a^{\frac{5}{6}}$

B. $a^{5}$

C. $a^{\frac{2}{3}}$

D. $a^{\frac{7}{6}}$

Xem đáp án

Chọn D

Với a>0, ta có $P = a^{\frac{2}{3}} \sqrt{a} = a^{\frac{2}{3}} a^{\frac{1}{2}} = a^{\frac{7}{6}}$ .

Câu 12:

Tổng lập phương các nghiệm thực của phương trình

3^{x^{2} - 4 x + 5} = 9

là

A. 26

B. 27

C. 28

D. 25

Xem đáp án

Chọn C

Ta có phương trình: $3^{x^{2} - 4 x + 5} = 9 \Leftrightarrow 3^{x^{2} - 4 x + 5} = 3^{2} \Leftrightarrow x^{2} - 4 x + 5 = 2 \Leftrightarrow [\begin{array}{l} x = 1 \\ x = 3 \end{array}$ .

Tổng lập phương các nghiệm thực của phương trình là: $1^{3} + 3^{3} = 28$ .

Câu 13:

Tìm số nghiệm của phương trình

\log_{3} (2 x - 1) = 2

A. 1

B. 5

C. 2

D. 0

Xem đáp án

Chọn A

$\log_{3} (2 x - 1) = 2 \Leftrightarrow 2 x - 1 = 3^{2} \Leftrightarrow x = 5$ .

Vậy phương trình có 1 nghiệm.

Câu 14:

Họ nguyên hàm của hàm số

f (x) = x^{2}

là

A. $\int x^{2} d x = \frac{x^{3}}{3} + C$

B. $\int x^{2} d x = \frac{x^{2}}{3} + C$

C. $\int x^{2} d x = \frac{x^{3}}{3}$

D. $\int x^{2} d x = 2 x + C$

Xem đáp án

Chọn A

Ta có $\int x^{2} d x = \frac{x^{3}}{3} + C$ .

Câu 15:

Một nguyên hàm của hàm số

f (x) = {(x + 1)}^{3}

là

A. $F (x) = 3 {(x + 1)}^{2}$ .

B. $F (x) = \frac{1}{3} {(x + 1)}^{2} .$

C. $F (x) = \frac{1}{3} {(x + 1)}^{2} .$

D. $F (x) = \frac{1}{3} {(x + 1)}^{2} .$

Xem đáp án

Chọn C

Áp dụng hệ quả chọn đáp án C.

Câu 16:

Cho hàm số y=f(x) có đạo hàm liên tục trên đoạn [-1;1] thỏa mãn

\int_{- 1}^{1} f^{'} (x) d x = 5

và f(-1)=4. Tìm f(1) .

A. f(1) = -1.

B. f(1) = 1

C. f(1) = 9

D. f(1) = -9

Xem đáp án

Chọn C

$\int_{- 1}^{1} f^{'} (x) d x = 5 = > f (1) - f (- 1) = 5 \Rightarrow f (1) - 4 = 5 \Rightarrow f (1) = 9$ .

Câu 17:

Tích phân

I = \int_{1}^{2} (\frac{1}{x} + 2) d x

bằng

A. I = ln2 + 2.

B. I = ln2 + 1.

C. I = ln2 - 1.

D. I = ln2 + 3.

Xem đáp án

Chọn A

Ta có: $I = \int_{1}^{2} (\frac{1}{x} + 2) d x = {(\ln |x| + 2 x) |}_{1}^{2} = \ln 2 + 4 - 2 = \ln 2 + 2 .$ .

Câu 18:

Cho a,b là hai số thực thỏa mãn a+6i=2-2bi, với i là đơn vị ảo. Giá trị của a+b bằng

A. -1

B. 1

C. -4

D. 5

Xem đáp án

Chọn A

Ta có $a + 6 i = 2 - 2 b i \Leftrightarrow \{\begin{cases} a = 2 \\ 6 = - 2 b \end{cases} \Leftrightarrow \{\begin{cases} a = 2 \\ b = - 3 \end{cases} \Rightarrow a + b = - 1$ .

Câu 19:

Cho số phức

z_{1} = 3 + 2 i, z_{2} = 6 + 5 i

. Tìm số phức liên hợp của số phức

z = 6 z_{1} + 5 z_{2}

A. $z$ = 51 + 40i.

B. $z$ = 51 - 40i.

C. $z$ = 48 + 37i.

D. $z$ = 48 - 37i.

Xem đáp án

Chọn D

Ta có: $z = 6 z_{1} + 5 z_{2} = 6 (3 + 2 i) + 5 (6 + 5 i) = 48 + 37 i$ .

Suy ra $\bar{z} = 48 - 37 i$ .

Câu 20:

Điểm nào trong hình vẽ bên là điểm biểu diễn của số phức z = -1 + 2i?

A. N

B. P

C. M

D. Q

Xem đáp án

Chọn D

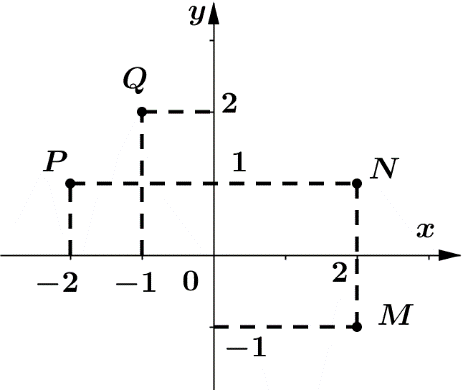
Vì z=-1+2i nên điểm biểu diễn số phức z có tọa độ (-1;2) , đối chiếu hình vẽ ta thấy đó là điểm Q.

Câu 21:

Thể tích của khối lập phương cạnh 2a bằng

A. 8a

B. 8a³

C. a³

D. 6a³

Xem đáp án

Chọn B

Thể tích khối lập phương cạnh 2a là

V = {(2 a)}^{3} = 8 a^{3}

Câu 22:

Cho khối chóp có diện tích đáy bằng 6cm²và có chiều cao là 2cm. Thể tích của khối chóp đó là:

A. 6cm³

B. 4cm³

C. 3cm³

D. 12cm³

Xem đáp án

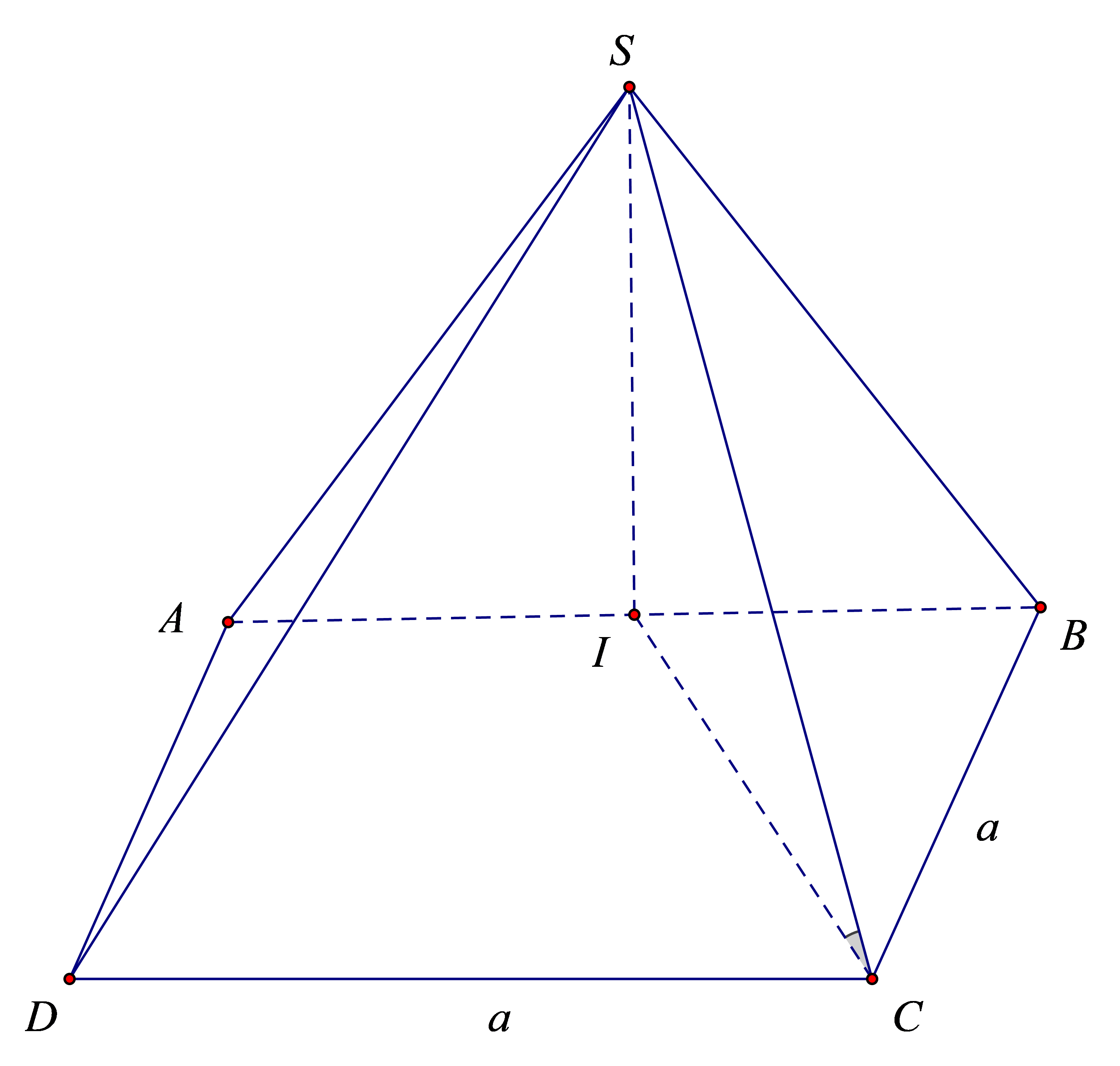
Chọn B

Thể tích của khối chóp là: $V = \frac{1}{3} h . S_{d a y} = \frac{1}{3} .2.6 = 4 (c m^{3})$ .

Câu 23:

Cho khối nón có bán kính đáy

r = \sqrt{3}

và chiều cao h=4. Tính thể tích V của khối nón đã cho.

A. $V = 16 π \sqrt{3}$ .

B. $V = 12 π$ .

C. $V = 4 π .$

D. 4.

Xem đáp án

Chọn C

$V = \frac{1}{3} . π . r^{2} . h = 4 π$ .

Câu 24:

Tính thể tích V của khối trụ có bán kính đáy r=10cm và chiều cao h=6cm.

A. $V = 120 π {cm}^{3} .$

B. $V = 360 π {cm}^{3} .$

C. $V = 200 π {cm}^{3}$ .

D. $V = 600 π {cm}^{3}$ .

Xem đáp án

Chọn D

Thể tích khối trụ là: $V = π r^{2} h = π {.10}^{2} .6 = 600 π {cm}^{3}$ .

Câu 25:

Trong không gian với trục hệ tọa độ Oxyz, cho

\vec{a} = - \vec{i} + 2 \vec{j} - 3 \vec{k} .

Tọa độ của vectơ

\vec{a}

là:

A. $\vec{a} (- 1; 2; - 3$ ).

B. $\vec{a} (2; - 3; - 1$ ).

C. $\vec{a} (- 3; 2; - 1$ ).

D. $\vec{a} (2; - 1; - 3$ ).

Xem đáp án

Chọn A

Ta có $\vec{a} = x \vec{i} + y \vec{j} + z \vec{k} \Leftrightarrow \vec{a} (x; y; z)$ nên $\vec{a} (- 1; 2; - 3) .$ Do đó Chọn A

Câu 26:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình

x^{2} + y^{2} + z^{2} + 4 x - 2 y - 4 = 0

.Tính bán kính R của (S).

A. 1

B. 9

C. 2

D. 3

Xem đáp án

Chọn D

Giả sử phương trình mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 2 a x - 2 b y - 2 c z + d = 0 (a^{2} + b^{2} + c^{2} - d > 0)$

Ta có: a=-2, b=1, c=0, d=-4 => Bán kính $R = \sqrt{a^{2} + b^{2} + c^{2} - d} = 3$ .

Câu 27:

Trong không gian với hệ trục tọa độ Oxyz cho các điểm A(0;1;2) , B(2;-2;1) , C(-2;0;1) . Phương trình mặt phẳng đi qua A và vuông góc với BC là

A. 2x - y - 1 = 0.

B. -y + 2z - 3 = 0.

C. 2x - y + 1 = 0.

D. y + 2z - 5 = 0.

Xem đáp án

Chọn C

Ta có: $l = \sqrt{h^{2} + R^{2}}$ .

Vậy phương trình mặt phẳng đi qua A và vuông góc với BC có dạng: $- 2 (x - 0) + 1 (y - 1) = 0 \Leftrightarrow - 2 x + y - 1 = 0 \Leftrightarrow 2 x - y + 1 = 0$

Câu 28:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;-2;1); B(2;1;-1), véc tơ chỉ phương của đường thẳng AB là:

A. $\vec{u} = (1; - 1; - 2)$

B. $\vec{u} = (3; - 1; 0)$

C. $\vec{u} = (1; 3; - 2)$

D. $\vec{u} = (1; - 1; 0)$

Xem đáp án

Chọn C

Véctơ chỉ phương của đường thẳng là: $\vec{u} = \vec{A B} = (1; 3; - 2)$

Câu 29:

Chọn ngẫu nhiên hai số khác nhau từ 27 số nguyên dương đầu tiên. Xác suất để chọn được hai số có tổng là một số chẵn bằng:

A. $\frac{13}{27}$ .

B. $\frac{14}{27} .$

C. $\frac{1}{2}$ .

D. $\frac{365}{729} .$

Xem đáp án

Câu 30:

Cho hàm số

y = \frac{2 x - 1}{x + 1}

. Mệnh đề nào dưới đây là đúng.

A. Hàm số nghịch biến trên các khoảng $(- \infty; - 1) v à (1; + \infty)$ .

B. Hàm số đồng biến trên các khoảng

(- \infty; - 1) v à (- 1; + \infty)

C. Hàm số luôn nghịch biến trên R.

D. Hàm số đồng biến trên R.

Xem đáp án

Câu 31:

Gọi M,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số

y = \frac{3 x - 1}{x - 3}

trên đoạn [0;2] . Tính 2M-m.

A. $2 M - m = \frac{- 14}{3}$

B. $2 M - m = \frac{- 13}{3}$

C. $2 M - m = \frac{17}{3}$

D. $2 M - m = \frac{16}{3}$

Xem đáp án

Câu 32:

Tập nghiệm của bất phương trình

\log_{2} (x - 1) \geq - 1

A. $[\frac{- 1}{2}; + \infty)$

B. $(- 1; - \frac{1}{2}]$

C. $(- \infty; - \frac{1}{2}]$

D. $[1; + \infty)$

Xem đáp án

Câu 33:

Cho

\int_{0}^{1} [f (x) - 2 g (x)] d x = 12

và

\int_{0}^{1} g (x) d x = 5

, khi đó

\int_{0}^{1} f (x) d x

bằng

A. -2.

B. 12.

C. 22.

D. 2.

Xem đáp án

Câu 34:

Cho hai số phức

z_{1} = 2 + i

và

z_{2} = - 3 + i

. Phần ảo của số phức

z_{1} \bar{z_{2}}

bằng

A. -5

B. -5i

C. 5

D. 5i

Xem đáp án

Chọn A

Ta có $z_{1} \bar{z_{2}} = (2 + i) (- 3 - i) = - 5 - 5 i$ .

Vậy phần ảo của số phức

z_{1} z_{2}

bằng -5.

Câu 35:

Cho khối chóp S.ABC có

S A ⊥ (A B C)

, tam giác ABC vuông tại B, AC=2a, BC=a, SB=

2 a \sqrt{3}

. Tính góc giữa và mặt phẳng (SBC) .

A. 4 $5 °$ .

B. 3 $0 ° .$

C. 6 $0 ° .$

D. 9 $0 ° .$

Xem đáp án

Câu 36:

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng $a \sqrt{2} .$ Tính khoảng cách d từ O tâm của đáy ABCD

đến một mặt bên ttheo a.

A. $d = \frac{a \sqrt{5}}{2} .$

B. $d = \frac{a \sqrt{3}}{2} .$

C. $d = \frac{2 a \sqrt{5}}{3} .$

D. $d = \frac{a \sqrt{2}}{3} .$

Xem đáp án

Câu 37:

Trong không gian Oxyz, cho hai điểm I(1;1;1) và A(1;2;3) . Phương trình của mặt cầu có tâm I và đi qua A là

A. ${(x + 1)}^{2} + {(y + 1)}^{2} + {(z + 1)}^{2} = 29 .$

B. ${(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 1)}^{2} = 5$ .

C. ${(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 1)}^{2} = 25 .$

D. $x + 1^{2} + y + 1^{2} + {(z + 1)}^{2} = 5$ .

Xem đáp án

Chọn B

Vì mặt cầu (S) có tâm I(1;1;1) và đi qua A(1;2;3) nên mặt cầu (S) có tâm I(1;1;1) và có bán kính là $R = I A = \sqrt{5}$ .

Suy ra phương trình mặt cầu (S) là: ${(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 1)}^{2} = 5$ .

Câu 38:

Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới đây là phương trình tham số của đường thẳng đi qua hai điểm A(1;0;1) và B(3;2;-1) .

A. $\{\begin{cases} x = 1 + t \\ y = 1 + t \\ z = - 1 - t \end{cases}, t \in R$

B. $\{\begin{cases} x = 3 + t \\ y = 2 - t \\ z = - 1 - t \end{cases}, t \in R$

C. $\{\begin{cases} x = 1 - t \\ y = - t \\ z = 1 + t \end{cases}, t \in R$

D. $\{\begin{cases} x = 2 + t \\ y = 2 + t \\ z = - 2 - t \end{cases}, t \in R$

Xem đáp án

Câu 39:

Nếu hàm số f(x) có đạo hàm là

f^{'} (x) = x^{2} (x + 2) (x^{2} + x - 2) {(x - 1)}^{4}

thì điểm cực trị của hàm số f(x) là

A. x = 0.

B. x = 2.

C. x = 1.

D. x = -2.

Xem đáp án

Chọn C

$f^{'} (x) = x^{2} (x + 2) (x^{2} + x - 2) {(x - 1)}^{4} = x^{2} {(x + 2)}^{2} {(x - 1)}^{5} f^{'} (x) = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ x = - 2 \\ x = 1 \end{array}$

Bảng xét dấu:

Vậy hàm số đạt cực trị tại x=1.

Câu 40:

Số nghiệm nguyên của bất phương trình

{(17 - 12 \sqrt{2})}^{x} \geq {(3 + \sqrt{8})}^{x^{2}}

là

A. 3

B. 1

C. 2

D. 4

Xem đáp án

Chọn A

Ta có: $(3 + \sqrt{8}) = {(3 - \sqrt{8})}^{- 1}, (17 - 12 \sqrt{2}) = {(3 - \sqrt{8})}^{2}$

Do đó ${(17 - 12 \sqrt{2})}^{x} \geq {(3 + \sqrt{8})}^{x^{2}} \Leftrightarrow {(3 - \sqrt{8})}^{2 x} \geq {(3 + \sqrt{8})}^{x^{2}} \Leftrightarrow {(3 + \sqrt{8})}^{- 2 x} \geq {(3 + \sqrt{8})}^{x^{2}}$

$\Leftrightarrow - 2 x \geq x^{2} \Leftrightarrow - 2 \leq x \leq 0$ . Vì x nhận giá trị nguyên nên $x \in \{- 2; - 1; 0\}$ .

Câu 41:

Cho hàm số f(x) liên tục trên R và có

\int_{0}^{1} f (x) d x = 2, \int_{0}^{3} f (x) d x = 6

. Tính

I = \int_{- 1}^{1} f (| 2 x - 1 |) d x

A. I = 8

B. I = 16

C. I = 3/2

D. I = 4.

Xem đáp án

Câu 42:

Cho số phức z=a+bi (với

a, b \in ℝ

) thỏa |z|(2+i)=z-1+i(2z+3) . Tính S=a+b.

A. S = -1.

B. S = 1.

C. S = 7.

D. S = -5.

Xem đáp án

Chọn A

$|z| (2 + i) = z - 1 + i (2 z + 3) \Leftrightarrow |z| (2 + i) + 1 - 3 i = z (1 + 2 i) \Leftrightarrow (1 + 2 |z|) + (|z| - 3) i = z (1 + 2 i)$

Suy ra: ${(1 + 2 |z|)}^{2} + {(|z| - 3)}^{2} = 5 {|z|}^{2} \Leftrightarrow |z| = 5$

Khi đó, ta có: $5 (2 + i) = z - 1 + i (2 z + 3) \Leftrightarrow z (1 + 2 i) = 11 + 2 i \Leftrightarrow z = \frac{11 + 2 i}{1 + 2 i} = 3 - 4 i$

Vậy S=a+b=3-4=-1.

Câu 43:

Cho hình chóp S.ABCD với ABCD là hình vuông cạnh a. Mặt bên SAB là tam giác cân tại S và nằm trên mặt phẳng vuông góc với mặt phẳng đáy. Cạnh bên SC tạo với đáy một góc

60 °

. Tính thể tích khối chóp S.ABCD.

A. $\frac{a^{3} \sqrt{15}}{2}$

B. $\frac{a^{3} \sqrt{15}}{6}$

C. $\frac{a^{3} \sqrt{6}}{3}$

D. $\frac{a^{3} \sqrt{3}}{6}$

Xem đáp án

Câu 44:

Một hoa văn trang trí được tạo ra từ một miếng bìa mỏng hình vuông cạnh bằng 10cm bằng cách khoét đi bốn phần bằng nhau có hình dạng parabol như hình bên. Biết AB=5cm, OH=4cm. Tính diện tích bề mặt hoa văn đó.

A. $\frac{160}{3} {cm}^{2}$

B. $\frac{140}{3} {cm}^{2}$

C. $\frac{14}{3} {cm}^{2}$

D. ${50cm}^{2}$

Xem đáp án

Câu 45:

Trong không gian với hệ toạ độ Oxyz, cho đường thẳng

∆

là giao tuyến của hai mặt phẳng (P): z-1=0 và (Q): x+y+z-3=0. Gọi d là đường thẳng nằm trong mặt phẳng (P) , cắt đường thẳng

\frac{x - 1}{1} = \frac{y - 2}{- 1} = \frac{z - 3}{- 1}

và vuông góc với đường thẳng

∆

. Phương trình của đường thẳng d là

A. $\{\begin{cases} x = 3 + t \\ y = t \\ z = 1 + t \end{cases}$

B. $\{\begin{cases} x = 3 - t \\ y = t \\ z = 1 \end{cases}$

C. $\{\begin{cases} x = 3 + t \\ y = t \\ z = 1 \end{cases}$

D. $\{\begin{cases} x = 3 + t \\ y = - t \\ z = 1 + t \end{cases}$

Xem đáp án

Câu 46:

Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ. Hỏi hàm số y=f(f(x)) có bao nhiêu điểm cực trị?

A. 6

B. 7

C. 8

D.9

Xem đáp án

Câu 47:

Cho

\log_{9} x = \log_{12} y = \log_{16} (x + y)

. Giá trị của tỷ số

\frac{x}{y}

là.

A. 2

B. $\frac{1 - \sqrt{5}}{2}$

C.1

D. $\frac{- 1 + \sqrt{5}}{2}$

Xem đáp án

Câu 48:

Cho hàm số y=f(x) . Hàm số y=f'(x) có đồ thị như hình vẽ. Biết phương trình f'(x)=0 có bốn nghiệm phân biệt a, 0, b, c với a<0<b<c.

A. f(b) > f(a) > f(c).

B. f(a) > f(b) > f(c).

C. f(a) > f(c) > f(b).

D. f(c) > f(a) > f(b).

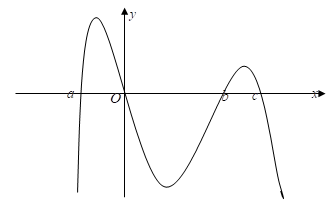
Xem đáp án

Chọn C

Bảng biến thiên của b:

Do đó ta có f(c)>f(b) (1)

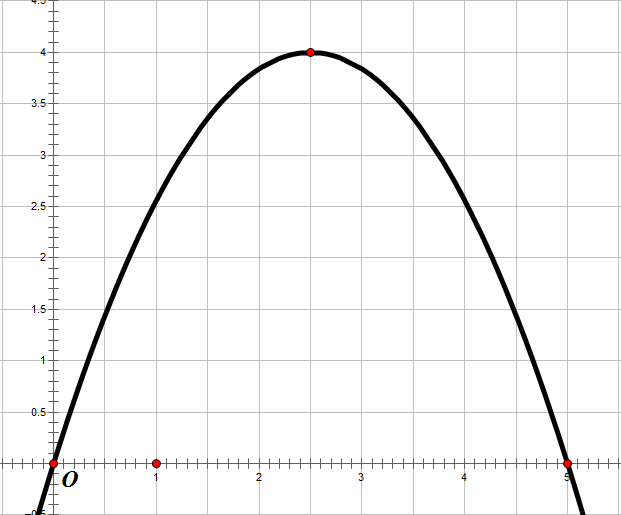
Ta gọi S1,S2,S3 lần lượt là các phần diện tích giới hạn bởi đồ thị hàm số b và trục hoành như hình bên.

$S_{2} > S_{1} + S_{3} \Leftrightarrow - \int_{0}^{b} f^{'} (x) d x > \int_{a}^{0} f^{'} (x) d x + \int_{b}^{c} f^{'} (x) d x \Leftrightarrow {- f (x)|}_{0}^{b} > {f (x)|}_{a}^{0} + {f (x)|}_{b}^{c}$

$\Leftrightarrow f (0) - f (b) > f (0) - f (a) + f (c) - f (b) \Rightarrow f (a) > f (c) (2)$

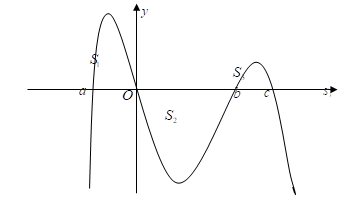
Từ (1) và (2) suy ra f(a)>f(c)>f(b) .

Câu 49:

Cho số phức z thỏa mãn |z-1-i| , số phức w thỏa mãn

|\bar{w} - 2 - 3 i| = 2

. Tìm giá trị nhỏ nhất của |z-w| .

A. $\sqrt{13} - 3$

B. $\sqrt{17} - 3$

C. $\sqrt{17} + 3$

D. $\sqrt{13} + 3$

Xem đáp án

Câu 50:

Trong không gian Oxyz, cho điểm $M (\frac{1}{2}; \frac{\sqrt{3}}{2}; 0)$ và mặt cầu $(S) : x^{2} + y^{2} + z^{2} = 8$ . Một đường thẳng đi qua điểm M và cắt (S) tại hai điểm phân biệt A, B. Diện tích lớn nhất của tam giác OAB bằng

A. 4

B. $2 \sqrt{7}$

C. $2 \sqrt{2}$

D. $\sqrt{7}$

Xem đáp án

Bắt đầu thi ngay

Bài thi liên quan

Đề số 1
- 33 câu hỏi
- 90 phút
Đề số 2
- 53 câu hỏi
- 90 phút
Đề số 3
- 50 câu hỏi
- 90 phút
Đề số 4
- 50 câu hỏi
- 90 phút
Đề số 5
- 50 câu hỏi
- 90 phút
Đề số 6
- 50 câu hỏi
- 90 phút
Đề số 7
- 50 câu hỏi
- 90 phút
Đề số 8
- 50 câu hỏi
- 90 phút
Đề số 9
- 50 câu hỏi
- 90 phút
Đề số 10
- 50 câu hỏi
- 90 phút