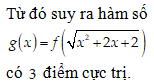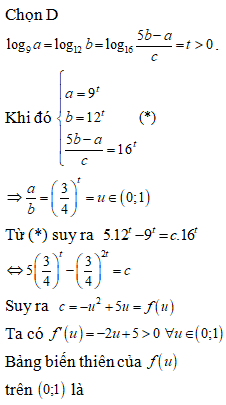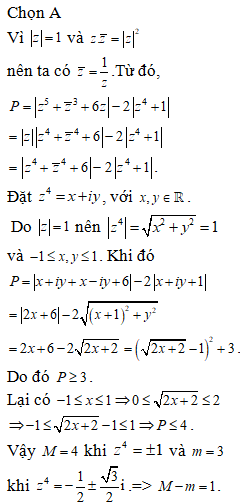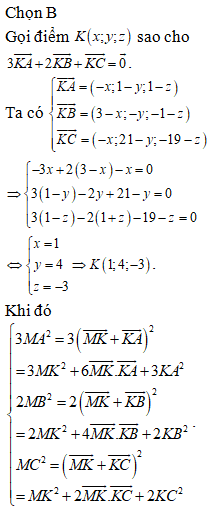Đề minh họa THPT Quốc gia môn Toán năm 2022 chọn lọc, có lời giải (30 đề)
Đề số 22
-
2812 lượt thi
-
50 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
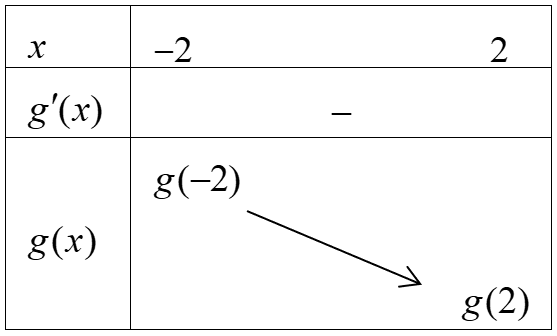
Chọn D
Số tập con gồm 5 phần tử của M chính là số tổ hợp chập 5 của 30 phần tử, nghĩa là bằng .
Câu 3:
Cho hàm số f(x) có bảng biến thiên như sau:
 Xem đáp án
Xem đáp án
Chọn A
Dựa vào bảng biến thiên ta có:
Hàm số đã cho đồng biến trên khoảng .
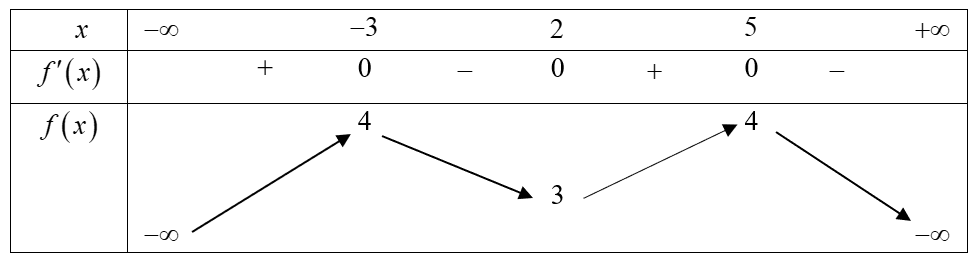
Câu 4:
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ dưới đây.
 Xem đáp án
Xem đáp án
Chọn A
Dựa vào BBT ta thấy giá trị cực đại của hàm số đã cho là y=1.
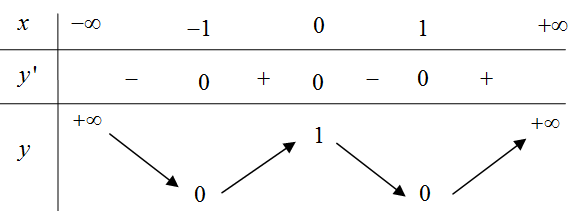
Câu 5:
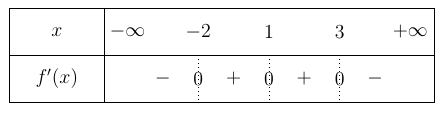
Cho hàm số y=f(x) có đạo hàm trên R và bảng xét dấu của đạo hàm như sau:
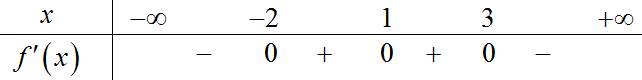
Hỏi hàm số y=f'(x) có bao nhiêu điểm cực trị?
 Xem đáp án
Xem đáp án
Chọn C
Từ bảng xét dấu ta thấy f'(x) đổi dấu khi x đi qua điểm nên hàm số có hai điểm cực trịCâu 6:
 Xem đáp án
Xem đáp án
Chọn A
Ta có: và nên đồ thị hàm số có một tiệm cận ngang là y=2.
Câu 7:
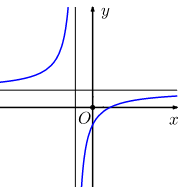
 Xem đáp án
Xem đáp án
Chọn D
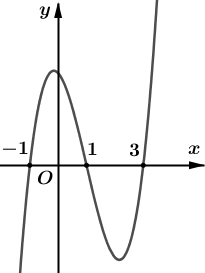
Đường cong trong hình trên không phải là đồ thị của hàm số bậc ba hoặc hàm số trùng phương, do đó phương án A và B là sai.
Đồ thị hàm số cắt trục tung tại điểm có tung độ , do đó phương án C sai.
Vậy phương án D đúngCâu 8:
 Xem đáp án
Xem đáp án
Chọn D
Ta có , hàm số y=f(x) luôn đồng biến trên R
Bảng biến thiên
Vậy đồ thị hàm số và trục Ox có 1 giao điểm.
Câu 9:
 Xem đáp án
Xem đáp án
Chọn B
Với a,b là hai số thực dương khác 1 và theo công thức đổi cơ số:
Câu 11:
 Xem đáp án
Xem đáp án
Chọn C
.
Câu 12:
 Xem đáp án
Xem đáp án
Chọn A
Ta có
Vậy tập nghiệm của phương trình đã cho là T={0;1}.
Câu 13:
 Xem đáp án
Xem đáp án
Chọn C
Ta có .
Vậy, phương trình đã cho có 2 nghiệm phân biệt.
Câu 14:
 Xem đáp án
Xem đáp án
Chọn C
Theo bảng nguyên hàm ta chọn câu sai là .
Câu 16:
 Xem đáp án
Xem đáp án
Chọn B
Ta có: .
Câu 18:
 Xem đáp án
Xem đáp án
Chọn B
Một số phức nếu có phần thực bằng 0 gọi là số thuần ảo, nên chọn B.
Câu 20:
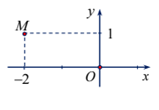
 Xem đáp án
Xem đáp án
Chọn D
Dựa vào hình vẽ ta thấy điểm M biểu diễn số phức z có phần thực bằng -2 và phần ảo bằng 1. Vậy số phức z = -2 + i.
Câu 21:
 Xem đáp án
Xem đáp án
Chọn C
.
Câu 22:
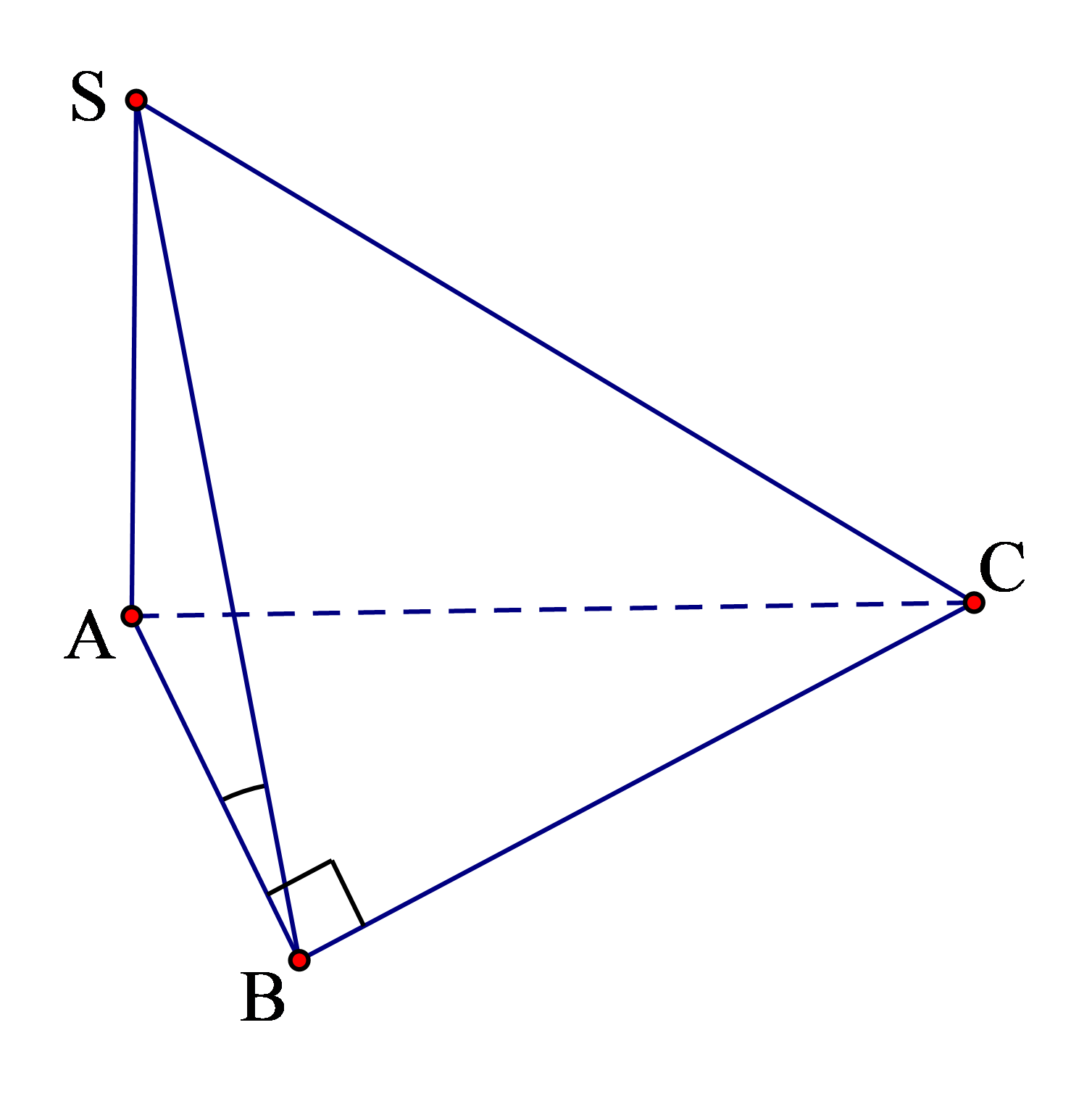
Thể tích của khối hộp chữ nhật ABCD.A'B'C'D' có các cạnh AB=3; AD=4; AA'=5 là
 Xem đáp án
Xem đáp án
Chọn D
Ta có: V=AB.AD.AA'=60
Câu 23:
 Xem đáp án
Xem đáp án
Chọn C
Bán kính của khối nón là .
Thể tích của khối nón là .
Câu 24:
Một khối trụ có chiều cao và bán kính đường tròn đáy cùng bằng R thì có thể tích là
 Xem đáp án
Xem đáp án
Chọn B
Áp dụng công thức thể tích khối trụ ta có:
Câu 25:
 Xem đáp án
Xem đáp án
Chọn A
Gọi I trung điểm của AB. Ta có: .
Câu 26:
 Xem đáp án
Xem đáp án
Chọn B
Ta có
Suy ra mặt cầu (S) có bán kính R=3.
Câu 27:
 Xem đáp án
Xem đáp án
Chọn B
Vectơ pháp tuyến của mặt phẳng (P): .
Vectơ pháp tuyến của mặt phẳng (Q): .
Theo yêu cầu bài toán: .Câu 28:
 Xem đáp án
Xem đáp án
Chọn A
Một vectơ chỉ phương của d là .
Câu 29:
 Xem đáp án
Xem đáp án
Chọn A
Số phần tử không gian mẫu:
Biến cố tổng hai mặt là 11: nên n(A)=2.
Suy ra .
Câu 32:
 Xem đáp án
Xem đáp án
Chọn B
Ta có: .
Vậy tập nghiệm bất phương trình là (2;4].
Câu 37:
 Xem đáp án
Xem đáp án
Chọn B
Tâm I là trung điểm AB => I(1;2;0) và bán kính .
Vậy .
Câu 38:
 Xem đáp án
Xem đáp án
Chọn C
Câu 41:
Hàm số f(x) liên tục trên . Biết rằng tồn tại hằng số a>0 để . Tính tích phân là
 Xem đáp án
Xem đáp án
Chọn B
Lấy đạo hàm hai vế biểu thức ta được.
. Suy ra .
Vậy .Câu 44:
 Xem đáp án
Xem đáp án
Chọn A
Lấy mốc thời gian là lúc bắt đầu đạp phanh. Giả sử to là thời điểm tàu dừng hẳn.
Khi đó
Như vậy từ lúc đạp phanh đến lúc tàu dừng hẳn là 10(s)
Quãng đường tàu di chuyển được trong khoảng thời gian 10(s) là .
Câu 48:
Cho hàm số f(x) có đạo hàm trên R, đồ thị hàm số y=f'(x) như trong hình vẽ bên.
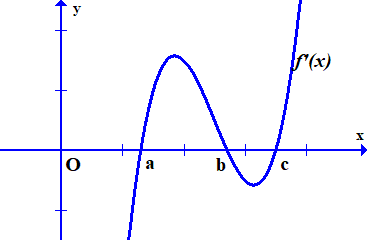
Hỏi phương trình f(x)=0 có tất cả bao nhiêu nghiệm biết f(a)>0?
 Xem đáp án
Xem đáp án
Chọn D
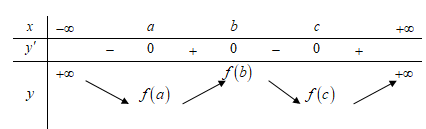
Mặt khác . Mà f(a)>0 nên phương trình vô nghiệm.

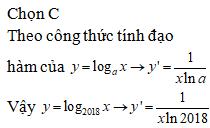

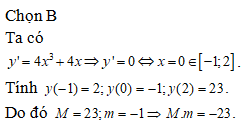

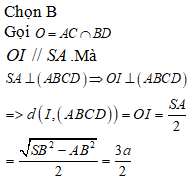


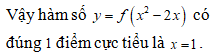
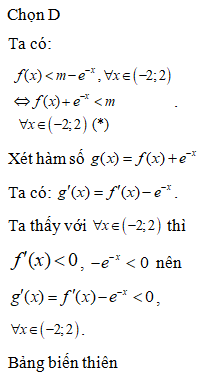
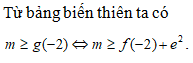
![Cho số phức z=[(2+6i)/(3-i)]^m, m nguyên dương (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/05/22-1653297259.png)