Chinh phục đề thi môn Toán vào lớp 6 có đáp án chi tiết năm 2024 (Đề 1)
-
1390 lượt thi
-
158 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
0,12 × 55 × 3 + 1,8 × 4,5 × 2.
=0,12 × 3 × 55 + 1,8 × 2 × 4,5
=0,36 × 55 + 3,6 × 4,5
=3,6 × 5,5 + 3,6 × 4,5
=3,6 × (5,5 + 4,5) = 3,6 × 10 = 36Câu 2:
 Xem đáp án
Xem đáp án
Chiều dài và chiều rộng tăng thêm cùng một độ dài thì chu vi tăng thêm 4 lần độ dài đó.
Độ dài mà chiều dài và chiều rộng tăng thêm là:
(180 ̶ 160) : 4 = 20 : 4 = 5 (cm).
Ta có hình vẽ:
Diện tích phần tăng thêm là diện tích 2 hình chữ nhật:
BEKC và DKFG.
Ta có thể coi phần diện tích tăng thêm chính là diện tích của hình chữ nhật DIHG.
Hình chữ nhật DIHG có 1 cạnh bằng 5 cm (chiều rộng tăng thêm 5 cm) và 1 cạnh bằng tổng chiều dài và chiều rộng hình chữ nhật ban đầu cộng thêm 5 cm (hình vẽ).
Tổng chiều dài và chiều rộng hình chữ nhật ban đầu (nửa chu vi) là: 160 : 2 = 80 (cm).
Diện tích phần tăng thêm là: 5 × (80 + 5) = 425 (cm2).Câu 3:
 Xem đáp án
Xem đáp án
Để hoàn thành công việc thì 15 công nhân mỗi ngày làm 8 giờ hoàn thành trong 20 ngày.
15 công nhân mỗi ngày làm 1 giờ làm trong
20 × 8 = 160 (ngày).
1 công nhân mỗi ngày làm 1 giờ làm trong
160 × 15 = 2400 (ngày).
1 công nhân mỗi ngày làm 10 giờ làm trong: 2400 : 10 = 240 (ngày).
5 công nhân mỗi ngày làm 10 giờ làm trong: 240 : 5 = 48 (ngày).Câu 4:
 Xem đáp án
Xem đáp án
– Nếu viết vào sau số 2021 một chữ số a ta được số .
Ta có: = 20210 + a.
20210 chia 37 dư nên để số chia hết cho 37 thì 8 + a phải chia hết cho 37, mà a là chữ số nên không có số a nào thỏa mãn.
– Nếu viết vào sau số 2021 hai chữ số a và b ta được số .
Ta có: = 202100 + .
202100 chia 37 dư 6 nên để số 2021ab chia hết cho 37 thì 6 + phải chia hết cho 37. Để được số bé nhất ta chọn viết: thêm chữ số ab là 31.Câu 5:
 Xem đáp án
Xem đáp án
Ta có 729 = 9 × 9 × 9.
Cạnh của hình lập phương bằng 9 cm.
Diện tích xung quanh của hình lập phương là:
9 × 9 × = 324 (cm2).Câu 6:
Bố An tặng chièu dài của bế cá hình hộp chữ nhật thêm 25%, tăng chiều rộng thêm 20% để phù hợp với thiết kế nhà. Bố An phảo thay đổi chiều cao như thế nào để thể tích của bể cá tăng thêm 20%?
 Xem đáp án
Xem đáp án
Thể tích của bể cá là tích của chiều dài, chiều rộng và chiều cao bể.
Tăng thêm chiều dài 25% và chiều rộng 20% thì tích chiều dài và chiều rộng bể mới gấp bể cũ là:
1,25 × 1,2 = 1,5 (lần).
Để thể tích bể cá tăng thêm 20% tức là thể tích bể mới gặp thể tích bể cũ là 1,2 lần thì tỉ số chiều cao của bể mới và bể cũ là: 1,2 : 1,5 = ![]() .
.
Hay chiều cao của bể mới bằng 80% chiều cao của bể cũ.
Như vậy bố An phải giảm chiều cao của bể cá 20% để thể tích của bể cá tăng thêm 20%.Câu 7:
 Xem đáp án
Xem đáp án
− Vì 1 tháng có ít nhất là 28 ngày, nhiều nhất là 31 ngày và mỗi tuần có 7 ngày nên số ngày “weekend day” không thể ít hơn 8 và nhiều hơn 10.
– Yến đã nghĩ con số 9, tháng đó có 8 ngày ““weekend day”, tháng trước có 10 ngày “weekend day”Câu 8:
 Xem đáp án
Xem đáp án
Trang bị rơi đầu tiên đánh số 387 thì trang cuối cùng sẽ phải là số lớn hơn và là số chẵn.
Do vậy trang cuối cùng phải là 738.
Có 738 – 387 + 1 = 352 (trang sách).
Vì mỗi tờ có hai trang nên số tờ rơi ra là 352 : 2 = 176 (tờ).Câu 9:
 Xem đáp án
Xem đáp án
Mỗi ông chồng sẽ bắt tay với 6 người phụ nữ không phải vợ mình nên 7 ông sẽ có số cái bắt tay là:
7 × 6 = 42 (cái bắt tay).
Các bà vợ chỉ không bắt tay chồng mình nên mỗi bà vợ sẽ bắt tay với 6 cặp vợ chồng còn lại nhưng trừ đi các cái bắt tay với các ông chồng khác đã tính ở trên nên coi như mỗi bà chỉ bắt tay với 6 bà còn lại.
Số cái bắt tay của riêng các bà với nhau là:
7 × 6 : 2 = 21 (cái bắt tay).
Tổng số cái bắt tay là: 42 + 21 = 63 (cái bắt tay).Câu 10:
 Xem đáp án
Xem đáp án
Số khẩu trang chưa vận chuyển đến chiếm số phần là:
(tổng số khẩu trang).
Số khẩu trang vận chuyển đến kho thiết bị chiếm số phần là:
(tổng số khẩu trang).
Tổng số khẩu trang công ty dự định tặng là:
(chiếc).Câu 11:
 Xem đáp án
Xem đáp án
- Chữ số 0 xuất hiện ở hàng đơn vị trong các số 1900, 1910, 1920, ..., 2020.
Từ 1900 đến 2020 có: (2020 – 1900) : 10 + 1 = 13 (số).
Vậy chữ số 0 xuất hiện 13 lần ở hàng đơn vị của các số
- Chữ số 0 xuất hiện ở hàng chục trong các số:
+ 1900, 1901,..., 1909: gồm 10 số.
+ 2000, 2001, ...,2009: gồm 10 số.
Vậy chữ số 0 xuất hiện 20 lần ở hàng chục của các số.
- Chữ số 0 xuất hiện ở hàng trăm trong các số
2000, 2001, ..., 2021: gồm 22 số.
Vậy chữ số 0 xuất hiện 22 lần ở hàng trăm của các số.
Trong số A có số chữ số 0 là 13 + 20 +22 = 55 (chữ số).Câu 12:
Một người bán được số cam như sau:
Người thứ nhất mua 9 quả và số cam còn lại.
Người thứ hai mua 18 quả và số cam còn lại.
Người thứ ba mua 27 quả và số cam còn lại.
…
Cuối cùng số cam vừa hết và số cam mỗi người mua bằng nhau. Hỏi người đó đã bán bao nhiêu quả cam? Xem đáp án
Xem đáp án
Người thứ nhất mua 9 quả nguyên, người thứ hai mua 18 quả nguyên, người thứ ba mua 27 quả nguyên, ... Vậy quy luật số nguyên quả cam ở đây là người mua sau hơn người mua liền trước 9 quả. Hay số quả cam nguyên được mua lập thành dãy số cách đều 9 đơn vị, bắt đầu từ 9..
+ Người cuối cùng mua một số nguyên quả cam thì vừa hết, có nghĩa phần dư còn lại là 0.
+ Người “áp chót” mua một số nguyên quả cam và số cam còn lại thì số cam còn lại khi này là số cam người cuối cùng mua.
+ Số cam mỗi người mua là như nhau.
Ta sử dụng sơ đồ đoạn thẳng:
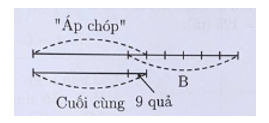
Đặc biệt lưu ý: Phần nguyên số cam người cuối cùng mua bằng phần nguyên số cam người "áp chót" mua và thêm 9 quả. Vậy số cam còn lại sau khi người " áp chót" mua một số nguyên quả cam là 9 quả.
Vậy số cam người cuối cùng mua là: 9 × 5 = 45 (quả).
Số người mua cam là: (45 ̶ 9) : 9 + 1= 5 (người).
Số cam người đó đem bán là: 45 × 5 = 225 (quả).Câu 13:
Khi trả bài kiểm tra môn Toán của lớp 5A cô giáo nói: Số điểm 10 chiếm 25%, số điểm 9 chiếm số phần trăm nhiều hơn phần trăm số điểm 10 là 6,25%. Như vậy có 18 bạn được điểm 10 hoặc điểm 9, tất cả học sinh trong lớp đều nộp bài kiểm tra. Hỏi lớp 5A có bao nhiêu học sinh?
 Xem đáp án
Xem đáp án
Học sinh đạt 9 chiếm: 25% + 6,25% = 31,25% (số học sinh của cả lớp).
Học sinh đạt 9 và 10 điểm chiếm: 25% + 31,25% = 56,25% (số học sinh của cả lớp).
Lớp 5A có số học sinh là: 18 : 56,25% = 32 (học sinh).
Câu 14:
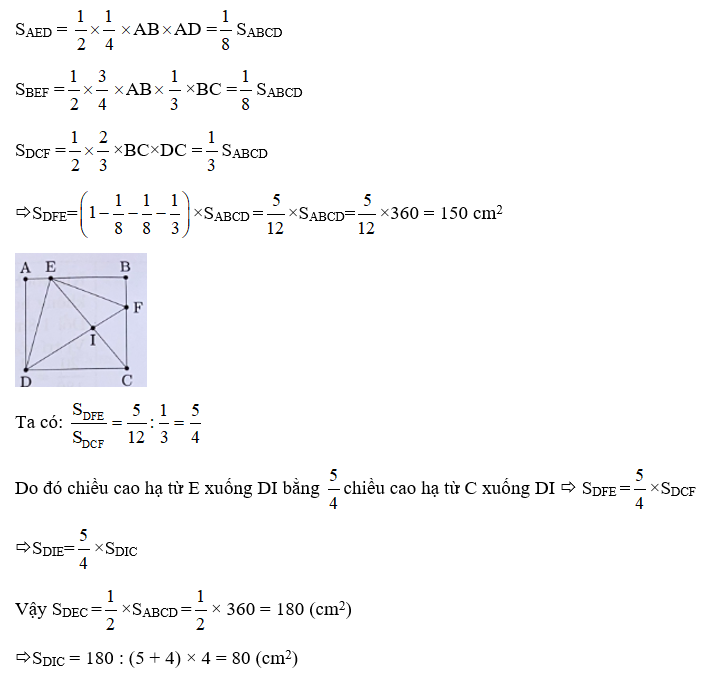
Cho hình vuông ABCD. Trên cạnh AB lấy điểm E, trên cạnh BC lấy điểm F sao cho AB = 4AE, BC = 4BF. Tính tỉ số
 Xem đáp án
Xem đáp án
Ta có
(vì chung đường cao vẽ từ D đến AB; )
Tương tự
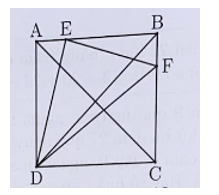
Suy ra:
Vậy .
Câu 15:
Trên một đoạn đường quốc lộ chạy song song với đường tàu, một hành khách ngồi trên ô tô nhìn thấy đầu tàu chạy ngược chiều còn cách ô tô 150m và sau 11 giây ô tô là 36 km/giờ và vận tốc của đoàn tàu 54km/giờ.
 Xem đáp án
Xem đáp án
Nhận xét: đoàn tàu và ô tô chuyển động ngược chiều.
Quãng đường cả hai đi được bằng 150m + độ dài đoàn tàu.
36 km/giờ = 10 m/giây; 54 km/giờ = 15 (m/giây).
Quãng đường đoàn tàu đi được trong 11 giây là 15 × 11 = 165 (m).
Quãng đường ô tô đi được trong 11 giây là 10 × 11 = 110 (m).
Tổng quãng đường ô tô và tàu đi được là 165 + 110 = 275 (m).
Đoàn tàu dài là 275 – 150 = 125 (m).
Câu 16:
 Xem đáp án
Xem đáp án
Trung bình mỗi trang phải dùng 2,5 chữ số. Như vậy phải bù vào:
Từ trang 1 đến trang 9 là (2,5 – 1) × 9 = 13,5 (chữ số).
Từ trang 10 đến trang 99 là (2,5 − 2) × 90 = 45 (chữ số).
Do vậy từ trang 1 đến trang 99 phải bù vào là: 13,5+45 = 58,5 (chữ số).
Mỗi trang có 3 chữ số thừa ra được là: 3 – 2,5 = 0,5 (chữ số).
Vậy số trang có 3 chữ số là: 58,5 : 0,5 = 117 (trang).
Số trang của quyển sách đó là: 117 + 99 = 216 (trang).Câu 18:
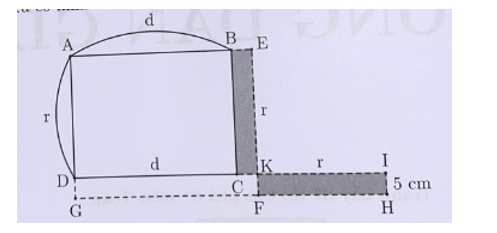
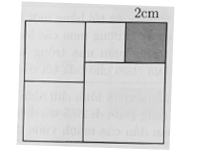
Hình chữ nhật hiển thị trên hình vẽ được chia thành 5 hình vuông nhỏ. Chiều dài của hình chữ nhật là bao nhiêu xăng-ti-mét biết cạnh của hình vuông tô đâm là 2 cm?
 Xem đáp án
Xem đáp án
Ký hiệu các điểm như hình vẽ. Vì 5 hình đều là hình vuông nên: CD = DI = IH = HC = 2 cm.
Từ đó có FI = FH + HI = LF = LK = KI = 2 + 2 = 4 (cm).
Chiều rộng của hình chữ nhật là: LB = LF + BF = 4 + 2 = 6 (cm).
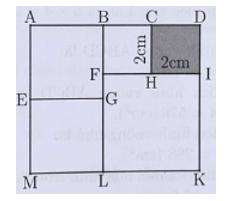
Do ABGE và EGLM là các hình vuông nên cạnh của chúng t bằng nhau nên GL = GB = LM = LB : 2 = 6 : 2 = 3 (cm).
Vậy chiều dài hình chữ nhật là:
MK = LM + LK = 3 + 4 = 7 (cm).Câu 19:
 Xem đáp án
Xem đáp án
Hộp loại II có 5 chiếc bút mà tổng số bút là 31 chiếc nên Dũng mua nhiều nhất chỉ được 6 hộp.
Tổng số bút trong hộp I chia hết cho 3 (vì mỗi hộp loại I có 3 chiếc bút), do đó tổng số bút loại II Dũng mua là một số chia cho 3 dư 1.
Số hộp bút loại II Dũng mua chỉ có thể là: 1, 2, 3, 4, 5, 6.
Xét các trường hợp ta thấy số hộp bút loại II chỉ có thể là 2 hoặc 5 (vì 2 × 5 = 10, 5 × 5 = 25 là các số chia 3 dư 1).
- TH 1: Nếu có 5 hộp bút loại II thì giá tiền mua nó là: 5 × 30000 = 150000 (đồng).
Số bút loại I là 31 − 5 × 5 = 6 (chiếc).
Số hộp bút loại I là 6 : 3 = 2 (hộp).
Giá tiền mua bút loại I là 2 × 20000 = 40000(đồng).
Tổng số tiền mua bút là: 150000 + 40000 = 190000 (đồng) (Không đúng).
- TH 2: Nếu có 2 hộp bút loại II thì giá tiền mua nó là: 2 × 30000 = 60000 (đồng).
Số bút loại I là 31 − 2 × 5 = 21 (chiếc).
Số hộp bút loại I là 21 : 3 = 7 (hộp).
Giá tiền mua bút loại I là 7 × 20000 = 140000 (đồng).
Tổng số tiền mua bút là: 60000 + 140000 = 200000 (đồng).
Vậy Dũng mua số hộp bút là 7 + 2 = 9 (hộp).Câu 20:
 Xem đáp án
Xem đáp án
Mỗi chú mèo có 2 tai và 1 đuôi nên tổng số tai mèo gấp đôi tổng số đuôi, vậy số đuôi mèo là: 15 : (2 + 1) = 5 (cái). Số mèo bằng số đuôi mèo.
Số chân mèo nhà Lan là 5 × 4 = 20 (cái).Câu 21:
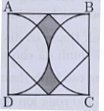
Cho hình vuông ABCD có chu vi là 96 cm.Tính diện tích phần tô đậm.
 Xem đáp án
Xem đáp án
Cạnh hình vuông ABCD là: 96 : 4 = 24 (cm).
Diện tích hình vuông ABCD là: 24 × 24 = 576 (cm2).
Diện tích hình vuông nhỏ là: 576 : 2 = 288 (cm2).
Bán kính của mỗi nửa hình tròn là: 24 : 2 = 12 (cm).
Diện tích một nửa hình tròn: 12 × 12 × 3,142 = 226,08 (cm2).
Diện tích phần tô đậm: 288 – 226,08 = 61,92 (cm2).
Câu 22:
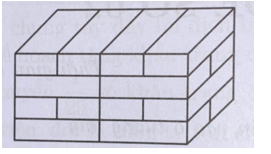
Mỗi viên gạch dạng hình hộp chữ nhật có chiều dài 20 cm, chiều rộng 10 cm, chiều cao 5 cm. Người ta xếp các viên gạch đó tạo thành một khối gạch dạng hình hộp chữ nhật (như hình vẽ). Tính diện tích xung quanh và thể tích khối gạch.
 Xem đáp án
Xem đáp án
Chiều dài của khối gạch là: 10 × 4 = 40 (cm).
Chiều rộng của khối gạch là 20 cm.
Chiều cao của khối gạch là: 5 × 4 = 20 (cm).
Diện tích xung quanh của khối gạch là: (40 + 20) × 2 × 20 = 2400 (cm2).
Thể tích của khối gạch là: 40 × 20 × 20 = 16000 (cm3) = 16 (dm3).Câu 23:
 Xem đáp án
Xem đáp án
Số bị trừ bằng hiệu cộng với số trừ nên 2 lần số bị trừ bằng 1908.
Số bị trừ là 1908 : 2 = 954.
Tổng của số trừ và hiệu chính là số bị trừ 954.
Số trừ là (954 +180) : 2 = 567.Câu 24:
 Xem đáp án
Xem đáp án
390 tấn thóc gấp 26 tấn thóc số lần là 390 : 26 = 15 (lần).
Vận chuyển 390 tấn thóc quãng đường 74km hết 120 000 000 đồng thì vận chuyển 26 tấn thóc với quãng đường 74km hết số tiền là:
120000000 : 15 = 8000000 (đồng).
185km gấp 74km số lần là 185 : 74 = (lần)
Vận chuyển 26 tấn thóc 185km hết số tiền là 8000000 × = 20000000 (đồng).Câu 25:
 Xem đáp án
Xem đáp án
Bữa tối của Thoa có 2 phương án: hoa quả hoặc rau xanh.
Hoa quả có 3 lựa chọn: ổi, táo, bưởi.
Rau xanh có 2 lựa chọn: bắp cải và súp lơ.
Thoa có thể lựa chọn bữa tối theo số cách là 3 + 2 = 5 (cách).Câu 26:
 Xem đáp án
Xem đáp án
Coi chiều dài ban đầu là 100%;
Chiều dài mới tăng 20% so với chiều dài ban đầu là: 100% + 20% = 120%.
Coi chiều rộng ban đầu là 100%
Chiều rộng mới giảm 20% so với chiều rộng ban đầu là: 100% - 20% = 80%.
Diện tích của hình chữ nhật mới bằng 120% × 80% = 96% diện tích của hình chữ nhật ban đầu.
So với hình chữ nhật ban đầu, diện tích của hình chữ nhật mới giảm
100% – 96% = 4% và bằng 32 cm2.
Diện tích của hình chữ nhật ban đầu là 32 : 4% = 800 (cm2)Câu 27:
Yến và Mai phải hoàn thành kế hoạch “Vì Trường Sa thân yêu" do nhà trường phát động. Theo kế hoạch này, hai bạn sẽ hoàn thành trong 10 ngày. Thực tế Yến bị ốm nên Mai phải hoàn thành công việc một mình trong 15 ngày. Hỏi nếu Yến không bị ốm thì kế hoạch do một mình Yến thực hiện sau bao lâu sẽ hoàn thành?
 Xem đáp án
Xem đáp án
Mai và Yến hoàn thành kế hoạch trong 10 ngày nên 1 ngày
Mai và Yến cùng làm được là 1 : 10 = (kế hoạch).
Mai hoàn thành kế hoạch trong 15 ngày nên 1 ngày Mai làm được là
1 : 15 = (kế hoạch).
1 ngày Yến làm được là (kế hoạch).
Như vậy nếu chia công việc thành 30 phần bằng nhau thì 1 ngày Yến làm được 1 phần đó.
Do đó Yến làm một mình hoàn thành kế hoạch hết (ngày)Câu 28:
Một cửa hàng bán đồ điện đã liên tiếp giảm giá 2 lần, mỗi lần 10% so với giá trước đó. Tính ra cửa hàng vẫn còn lãi 13,4% so với giá vốn. Hỏi bình thường của hàng đó bán các mặt hàng lãi bao nhiêu phần trăm?
 Xem đáp án
Xem đáp án
Giá bán sau 2 lần giảm liên tiếp chiếm số phần trăm so với giá niêm yết là
(100% ̶ 10%) × (100% ̶ 10%) = 81%.
Giá bán sau 2 lần giảm liên tiếp chiếm số phần trăm so với giá vốn là:
100% + 13,4% = 113,4%.
Giá niêm yết chiếm số phần trăm so với giá vốn là: 113,4 : 81 × 100% = 140%.
Bình thường cửa hàng đó bán các mặt hàng lãi số phần trăm là: 140% – 100% = 40%.
Câu 29:
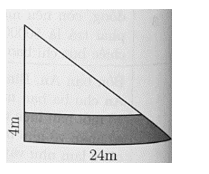
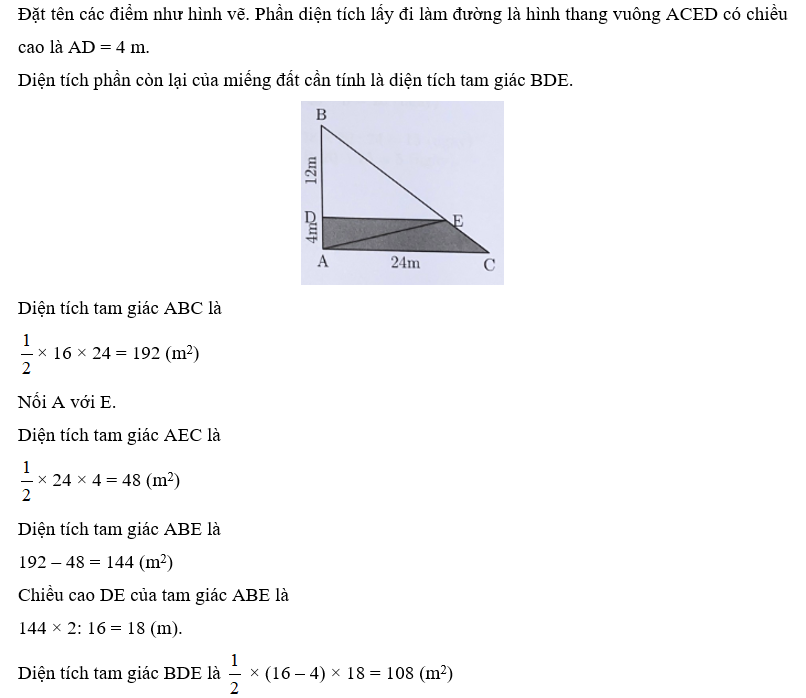
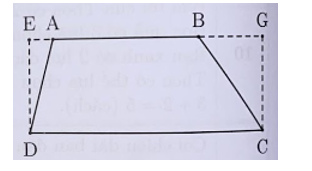
Một hình thang có đường cao là 10 m, hiểu hai đáy là 22 m. Kéo dài đáy nhỏ bằng đáy lớn để hình đã cho thành hình chữ nhật có chiều dài bằng đáy lớn, chiều rộng bằng đường cao hình thang. Diện atích được mở rộng thêm bằng diện tích hình thang cũ. Phần mở rộng lớn hơn có diện tích là 90 m2. Em hãy tính đáy lớn của hình thang ban đầu.
 Xem đáp án
Xem đáp án
Đáy BG của tam giác CBG là 90 × 2 : 10 = 18 (m).
Diện tích hình tam giác DAE là (22–18) × 10 : 2 = 20 (m2).
Diện tích hai phần mở rộng là 20 + 90 = 110 (m2).
Diện tích hình thang ABCD là 110 × 7=770 (m2).
Tổng hai đáy AB và CD là 770 × 2 : 10 = 154 (m).
Đáy CD dài là (154 + 22) : 2 = 88 (m).
Câu 30:
Có hai thùng cam: Thùng thứ nhất có số quả cam bằng thùng thứ hai; Nếu lấy 5 quả ở thùng thứ nhất chuyển sang thùng thứ hai thì thùng thứ nhất có số quả cam bằng thùng thứ hai. Tính số quả cam lúc đầu trong mỗi thùng.
 Xem đáp án
Xem đáp án
Lúc đầu, thùng thứ nhất có số quả cam bằng thùng thứ hai nên thùng thứ nhất có số cam bằng tổng số cam hai thùng.
Lúc sau, thùng thứ nhất có số quả cam bằng thùng thứ hai nên thùng thứ nhất có số cam bằng tổng số cam hai thùng.
5 quả ứng với (tổng số cam hai thùng).
Tổng số cam hai thùng là (quả).
Ban đầu thùng thứ nhất có (quả).
Thùng thứ hai có 175 – 75 = 100 (quả).Câu 32:
Cho dãy số: ,...
Tìm số hạng thứ 38 của dãy số. Xem đáp án
Xem đáp án
Nhận xét: Tử số của các phân số là 1. Mẫu là tích của hai số chẵn hoặc lẻ liên tiếp.
Số thứ 1.
Số thứ 2.
Số thứ 3.
…
Tổng quát: Phân số thứ n là: .
.
Vậy phân số thứ 38 của dãy số là .Câu 33:
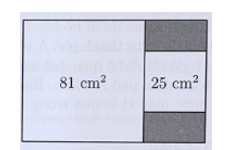
Miếng bìa hình chữ nhật được cắt thành hai miếng bìa hình chữ nhật bé có kích thước giống nhau và hai miếng bìa hình vuông có diện tích là 81 cm2 và 25 cm2. Tính tỉ số chu vi miếng bìa hình chữ nhật lớn và hình chữ nhật bé.
 Xem đáp án
Xem đáp án
Diện tích hai miếng bìa hình vuông là 81cm2 và 25cm2 nên cạnh hai hình vuông lần lượt là 9cm và 5cm. Do hai hình chữ nhật có kích thước giống nhau nên:
Chiều rộng miếng bìa hình chữ nhật bé là (9 − 5) : 2 = 2 (cm).
Chiều dài miếng bìa hình chữ nhật lớn là 9 + 5 = 14 (cm).
Chu vi miếng bìa hình chữ nhật lớn là (14 + 9) × 2 = 46 (cm).
Chu vi miếng bìa hình chữ nhật bé là (5 + 2) × 2 = 14 (cm).
Tỉ số chu vi:Câu 34:
 Xem đáp án
Xem đáp án
Chu vi bằng 3 lần chiều dài nên tỉ số nửa chu vi và chiều dài là:
Ta có sơ đồ:
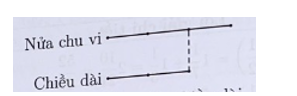
Theo sơ đồ thì chiều rộng bằng nửa chiều dài.
Chiều dài là: 20 × 2 = 40 (cm)
Diện tích hình chữ nhật là: 20 × 40 = 800 (cm2)
Câu 35:
 Xem đáp án
Xem đáp án
Ta giả sử khi mua bánh Pizza loại 30000 đồng thì mỗi chiếc bánh mua kèm thêm 1 cốc trà sữa có giá 10000 đồng. Như vậy số tiền mỗi suất ăn của các bạn lớp 5A là cần 40000 đồng.
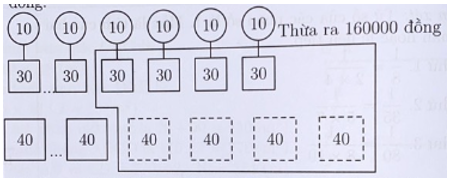
Vì nếu mua loại Pizza có giá 40000 đồng một chiếc thì 4 bạn không có bánh ăn nên để mỗi bạn lớp 5A đều được ăn bánh loại 40000 đồng thì cần thêm số tiền ngoài quỹ đã trích là: 40000 × 4 = 160000 (đồng).
Để mua mỗi bạn một bánh Pizza loại 30000 đồng và 1 cốc trà sữa có giá 10000 đồng mà vẫn thừa ra 160000 đồng thì số tiền cần thêm là:
160000 + 160000 = 320000 (đồng).
Số tiền cần thêm này chính là số tiền cần mua thêm cho mỗi bạn 1 cốc trà sữa 10000 đồng.
Vậy số bạn học sinh của lớp 5A là:
320000 : 10000 = 32 (học sinh).
Số tiền quỹ là 30000 × 160000 = 1120000 đồng.
Cách khác:
Số tiền quỹ trích ra là A.
Số tiền đủ để mua mỗi bạn 1 chiếc bánh loại 30000 đồng là B.
Số tiền đủ để mua mỗi bạn 1 chiếc bánh loại 40000 đồng là C.
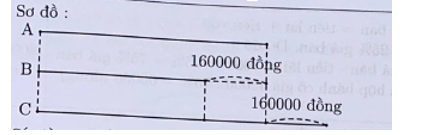
Số tiền đủ để mua loại bánh 40000 đồng nhiều hơn số tiền đủ để mua loại bánh 30000 đồng là 160000 + 160000 = 320000 (đồng)
Mỗi bạn học sinh khi mua bánh loại 40000 đồng đắt hơn bánh loại 30000 đồng là 40000 – 30000 = 10000 (đồng)
Số học sinh của lớp 5A là 320000 : 10000 = 32 (học sinh)
Số tiền quỹ lớp 5A trích ra là 30000 × 32 + 160000 = 1120000 (đồng).Câu 36:
 Xem đáp án
Xem đáp án
Số gạo dự trữ đủ cho 1 người ăn trong số ngày là: 150 × 20 = 3000 (ngày).
Thực tế:
Số gạo đủ ăn trong số ngày là: 20 – 8 = 12 (ngày).
Số người ăn thực tế là: 3000 : 12 = 250 (người).
Số người chuyển đến thêm là: 250 – 150 = 100 (người).Câu 37:
 Xem đáp án
Xem đáp án
Một ngày hai bạn cùng làm được (công việc).
Khi làm chung được 7 ngày, cả hai đã hoàn thành được (công việc).
Anh phải làm một mình công việc trong 9 ngày
Mỗi ngày Anh làm được (công việc).
Vậy, nếu làm một mình Anh cần ngày để hoàn thành hết công việc.Câu 38:
 Xem đáp án
Xem đáp án
Nhận xét: Khi bỏ thêm bi màu vàng vào trong hộp thì:
+ Số bi vàng tăng và tổng số bị tăng.
+ Số bi không phải màu vàng không đổi.
Số bi không phải màu vàng có trong hộp là:
200 × (100% – 45%) = 110 (viên).
Sau khi cho một số bi vàng vào hộp thì số bi không phải màu vàng chiếm 100% – 60% = 40% là 110 viên.
Vậy tổng số bi là: 110 : 40% = 275 (viên).
Người ta đã cho vào trong hộp số viên bi vàng là: 275 – 200 = 75 (viên bi).Câu 39:
 Xem đáp án
Xem đáp án
Nhận xét: giá bán = tiền lãi + tiền vốn.
Tiền lãi bằng 25% giá bán. Do đó
Tiền vốn = giá bán – tiền lãi = 100% – 25% = 75% giá bán
Cửa hàng bán hộp bánh có giá 45000 : 75% = 60000 (đồng).Câu 40:
 Xem đáp án
Xem đáp án
Nhận xét: Dãy gồm các số chẵn.
Số 0 có 1 số hạng.
Số 2 có 3 số hạng.
Số 4 có 5 số hạng.
…
→ Số 18 có 19 số hạng
Vậy dãy có số các số hạng nhỏ hơn 20 là :
1 + 3 + 5 +... + 19 = (19 + 1) × 10 : 2 = 100 (số hạng)Câu 41:
 Xem đáp án
Xem đáp án
- Nếu x > y thì nên .
Vậy y < 4, do đó y nhận các giá trị 1, 2, 3
+ Khi y = 1, 2 thì loại
+ Khi y = 3 thì , x = 12
- Nếu x < y thì: nên , vậy x < 4
+ Khi x = 1 thì loại.
+ Khi x = 2 thì , y = 8.
+ Khi x = 3 thì . LoạiCâu 42:
 Xem đáp án
Xem đáp án
Đi bộ 7 giờ và đi ngựa 5 giờ được 80km.
Đi ngựa 11 giờ rồi quay lại đi bộ 7 giờ thì di chuyển được 64km
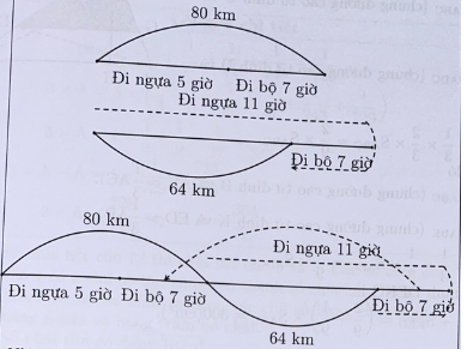
Nhìn vào sơ đồ thì 16 giờ đi ngựa được số ki-lô-mét là: 80 + 64 = 144 (km)
1 giờ người đó đi ngựa được số ki-lô-mét là: 144 : 16 = 9 (km).Câu 43:
Lớp 5A có số học sinh là học sinh trung bình, số học sinh giỏi bằng số học sinh khá và không có học sinh yếu kém. Biết số học sinh giỏi hơn số học sinh trung bình 2 bạn. Tính số học sinh của lớp 5A.
 Xem đáp án
Xem đáp án
Tổng số học sinh giỏi và khá chiếm số phần là (tổng số học sinh)
Số học sinh giỏi chiếm số phần là: (tổng số học sinh)
Số học sinh giỏi hơn số học sinh trung bình 2 bạn nên tổng số học sinh lớp 5A là: (học sinh).
Câu 44:
 Xem đáp án
Xem đáp án
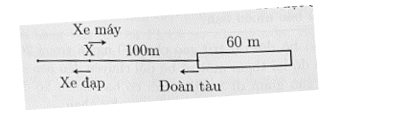
Đổi 36 km/giờ = 10 m/giây; 12 km/giờ = m/giây.
Tại cùng một thời điểm, đoàn tàu và xe đạp chuyển động cùng chiều với nhau; đoàn
tàu và xe máy chuyển động ngược chiều với nhau.
Trong 1 giây cả tàu và xe máy đi được quãng đường là: (m).
Vận tốc của đoàn tàu là: (m/giây) = 60 km/giờ.
Thời gian để đoàn tàu vượt qua người đi xe đạp là: (giây).
Câu 45:
Cho tam giác ABC, có BC = 6 cm, đường cao AH = 30 cm. Trên cạnh AB lấy điểm D [i]và E sao cho AE = ED = DB. Trên AC lấy điểm G và K sao cho AK = GK = GC. Tính diện tích hình DEKG
 Xem đáp án
Xem đáp án
Diện tích tam giác ABC là: 60 × 30 : 2 = 900(cm)
Nối KD và CD. Ta có
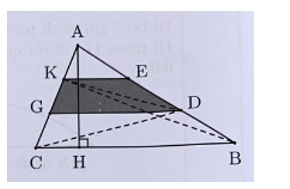
+) SADC = SABC (chung đường cao từ đỉnh C và AD = AB).
+) SKDG = SADC (chung đường cao từ đỉnh D và KG = AC).
Do đó SKDG = ×SABC = × SABC.
Diện tích của hình DEKG là: SDEKG = SKDG + SKED = × SABC = 300 (cm2)
Câu 47:
 Xem đáp án
Xem đáp án
Số chia hết cho 12 thì chia hết cho 3 và 4. Các số chia hết cho 4 có 2 chữ số tận cùng tạo thành số chia hết cho 4.
Muốn số đó bé nhất ta chọn các chữ số hàng chục nghìn, hàng nghìn và hàng trăm bé nhất.
Số phải tìm có dạng .
Giờ ta cần chọn c, d để c, d khác nhau và khác 0, 1, 2 thỏa mãn chia hết cho 4 đồng thời 1 + 0 + 2 + c + d chia hết cho 1.
Ta chọn được c = 3, d = 6 thỏa mãn.
Vậy số thỏa mãn đề bài là 10236.Câu 48:
 Xem đáp án
Xem đáp án
Vì số tiền loại 1000 bằng số tiền loại 2000 nên số tờ 1000 gấp đôi số tờ 2000.
Nếu thay 2 tờ tiền 1000 và 1 tờ tiền 2000 bởi 3 tờ tiền 5000 ta sẽ được toàn bộ 15 tờ 5000.
Khi đó tổng số tiền là 15 × 5000 = 75000 (đồng)
Số tiền chênh ra so với thực tế là 75000 – 42000 = 33000(đồng).
Mỗi lần thay 2 tờ 1000 và 1 tờ 2000 bằng 3 tờ 5000 thì số tiền chênh ra là
3 × 5000 − 2 × 1000 – 2000 = 11000 đồng.
Vậy số lần thay hay số tờ 2000 là 33000 : 11000 = 3(tờ). Số tờ 1000 là 6 tờ, số tờ 5000 là 6 tờ.Câu 49:
 Xem đáp án
Xem đáp án
Đường kính tăng lên 20% thì bán kính cũng tăng lên 20%.
Lúc đầu diện tích hình tròn là R × R × 3,14.
Lúc sau diện tích hình tròn là (1,2 × R) × (1,2 × R) × 3,14 = R × R × 3,14 × 1,44 = R × R × 3,14 × 144%.
Vậy diện tích tăng lên 44%.Câu 50:
 Xem đáp án
Xem đáp án
Ta có
(số thứ 2) = (số thứ 1) + 4 × 1
(số thứ 3) = (số thứ 2) + 4 × 2
...
(số thứ 100) = (số thứ 99) + 4 × 99.
Cộng theo từng vế và bỏ thành phần bằng nhau ta được
(số thứ 100) = (số thứ 1) + 4 × (1 + ... + 99)
= 3 + 4 ×Câu 51:
 Xem đáp án
Xem đáp án
Số vi khuẩn còn lại là: 1% × 2000 = 20 (con)
Thống kê theo thời gian số vi khuẩn như sau
40 phút lần 1: 20 × 2 (con).
40 phút lần 2: 20 × 2 × 2 (con).
...
40 phút lần n: 20 ×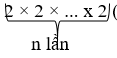 (con).
(con).
Kiểm tra thấy để số vi khuẩn phục hồi lại 2000 con thì n ít nhất phải bằng 7. Vậy cần ít nhất 280 phút để số vi khuẩn phục hồi lại như lúc đầu.
Câu 52:
 Xem đáp án
Xem đáp án
Gọi thời gian mà ô tô đi từ A tới B với vận tốc 45 km/giờ là t45 (giờ).
Gọi thời gian mà ô tô đi từ A tới B với vận tốc 60 km/giờ là t60 (giờ).
Trên cùng quãng đường thì vận tốc và thời gian là 2 đại lượng tỉ lệ nghịch.
Ta có mà hiệu t45 – t60 = 60 (phút)
Ta tính được t45 = 240 phút = 4 giờ.
Quãng đường AB dài là 4 × 45 = 180 (km).
Đi với vận tốc 50 km/giờ thì ô tô đến B hết thời gian là
180 : 50 = 3,6 (giờ) = 3 giờ 36 phút.Câu 53:
 Xem đáp án
Xem đáp án
Các khối lập phương không có bất cứ mặt nào được sơn màu đỏ là các khối lập phương nằm bên trong tạo thành khi bỏ các lớp mặt ngoài của khối lập phương lớn.
Ta có 27 = 3 × 3 × 3
Vậy cạnh hình lập phương lớn là 3 + 1 + 1 = 5 (dm).
Thể tích khối lập phương lớn là 5 × 5 × 5 = 125(dm3).Câu 54:
 Xem đáp án
Xem đáp án
112 viên bị tạo thành 112 khoảng cách.
Ta có 112 : 2 = 56
Viên số 1 đối diện viên số 1 + 56 = 57.
Viên số 2 đối diện viên 2 + 56 = 58.
…
Viên số 19 đối diện viên số 19 + 56 = 75.Câu 55:
 Xem đáp án
Xem đáp án
Vì trong bốn lọ bi còn lại, số bi màu đỏ gấp 3 lần số bi màu xanh nên tổng số bi còn lại phải là một số chia hết cho 4.
Tổng các số 23 + 24 + 25 + 28 + 39 = 139.
Ta thấy 139 chia 4 dư 3 mà tổng số bi còn lại chia hết cho 4 nên số bi An cho Bình chia 4 dư 3.
Trong các số 23, 24, 25, 28, 39 chỉ có 39 và 23 chia 4 dư 3. Thử 2 trường hợp thì lo cho đi là lo bi có 39 viên. 3 lọ 23, 24, 28 là bi đỏ và lọ 25 là bi xanh.Câu 56:
 Xem đáp án
Xem đáp án
Hiệu số tuổi mẹ với con nhỏ và mẹ với con lớn không thay đổi theo thời gian.
Tổng số tuổi 3 mẹ con 9 năm nữa là 48 + 3 × 15 = 93 (tuổi)
Mẹ hơn con nhỏ 30 tuổi và hơn con lớn 24 tuổi nên con lớn hơn con nhỏ 6 tuổi.
Ta có sơ đồ tuổi 3 mẹ con tại thời điểm 9 năm sau:
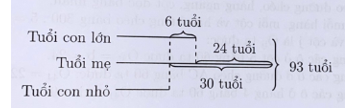
Tuổi của mẹ 9 năm nữa là (93 – 6 – 30) : 3 + 30 = 49 (tuổi)
Tuổi của mẹ hiện nay là 49 – 9 = 40 (tuổi).Câu 57:
 Xem đáp án
Xem đáp án
Với cách ngồi mỗi bàn 4 bạn có 5 bạn thừa ra. Giả sử với cách sắp xếp này ta cho thêm mỗi bàn một bạn nữa, như vậy số học sinh sẽ tăng thêm so với ban đầu là 5 + 5 × 1 = 10 (bạn).
Vậy lớp 5A có số bàn là 10 : (5 – 4) = 10 (bàn).Câu 58:
Thực đơn giải khát của một nhà hàng có 4 vị sữa, 9 vị kem và 3 cốc đựng kem khác kích cỡ. Mỗi người có thể mua một vị sữa hoặc một vị kem và đựng trong một loại cốc. Hỏi nhà hàng có thể phục vụ được tối đa bao nhiêu người để mỗi người đều có thực đơn khác nhau?
 Xem đáp án
Xem đáp án
Đồ uống gồm 4 vị sữa kết hợp 3 cỡ cốc cho ta 12 lựa chọn. 9 vị kem và 3 cỡ cốc cho ta 27 lựa chọn. Vậy nhà hàng phục vụ tối đa được 39 vị khách để mỗi người có thực đơn khác nhau.
Câu 59:
Cho tam giác ABC có diện tích 180 cm2. Trên cạnh BC lấy các điểm M và N sao cho BM = CN = . Nối AM, AN. Gọi O là trung điểm của AM, giao điểm của AN với CO là I, kéo dài BO cắt AN tại K. Tính diện tích tam giác OIK.
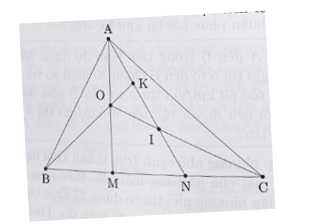
 Xem đáp án
Xem đáp án
Đầu tiên xác định tỉ số AK và AN
Ta có BM = CN = nên BM = CN = MN.
Theo đề bài:
BN = 2BM nên SBON = 2SBOM (chung chiều cao hạ từ O) (1).
Ta có OA = OM nên SBOM = SABO (chung chiều cao hạ từ B) (2).
Từ (1) và (2) suy ra SBON = 2SABO, mà hai tam giác chung đáy BO nên chiều cao hạ N gấp đôi chiều cao hạ A, kéo theo SBKN = 2SBKA, mà hai tam giác này chung chiều cao hạ từ B nên KN = 2KA hay AN = 3AK.
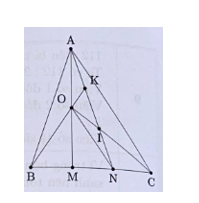
Xác định tỉ số AI và IN. Xét tam giác AMC có:
CN = MN nên SANM = SACN = SACM kéo theo SAMI =SACI
AO = OM nên SAOC = SMOC = SACM kéo theo SMCI =SACI
Vậy SMCI =SACI =SAMI hay SMCI =SACI =SAMI = SACM , ta được SAMI =SACM .
Ta lại có SANM = SACM nên SAMI =SANM , kéo theo AI= AN.
Như vậy ta được AN=3AK; AI= AN; KI= AN.
Vậy SOIK= SAON= SAMN= SABC= =10 cm2
Câu 60:
Mỗi ô trong hình vuông kích thước 5 x 5 (hình bên) được điền một trong các số từ 0 đến 24. Biết rằng tổng các số trong các hàng, các cột, hai đường chéo đều bằng nhau và các số trong các ô là khác nhau. Tìm a, b, c, d.
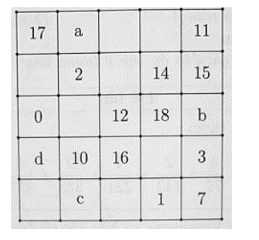
 Xem đáp án
Xem đáp án
Tổng các số trong bảng là: 1 + 2 + 3 + ... + 24 = 300.
Mà tổng các số theo đường chéo, hàng ngang, cột dọc bằng nhau;
Do đó tổng các số mỗi hàng, mỗi cột và hai đường chéo bằng 300 : 5 = 60.
Kí hiệu ô ở hàng i và cột j là Oij ta được:
Từ tổng các số trong các ô ở cột 5 bằng 60 ta được O35 = b = 24.
Từ tổng các số trong các ô ở đường chéo AC bằng 60 ta được: O44 = 22, từ O44 = 22 và tổng các số trong các ô ở hàng 4 bằng 60 ta được O41 = d = 9.

Từ tổng các số trong các ô ở đường chéo BD bằng 60 ta được O51 = 13 → O21 = 21
Từ đó: O23 = 8; O32 = 6; O14 = 5.
Còn 4 số: 23, 19, 04, 20 cần điền vào 4 ô: O12, O13, O52, O53.
Từ tổng các số trong các ô ở hàng 1 và hàng 5 bằng 60 ta được
O12 + O13 = 27; O52 + O53 = 39.
Từ tổng các số trong các ô ở cột 2 và cột 3 bằng 60 ta được
O12 + O52 = 42; O13 + O53 = 24.
Vậy O12 = a = 23; O52 = c = 19; O13 = 4; O53 = 20.
Kết luận: a = 23; b = 24; c = 19; d = 9.
Câu 62:
 Xem đáp án
Xem đáp án
Các số điện thoại “đẹp” có dạng:
• 0912ab3466: Các số dạng này, a có 3 lựa chọn và b có 2 lựa chọn trong các chữ số 5, 7, 8 do đó có 6 số dạng 0912ab3466.
• 0912ab3468: a có 2 lựa chọn và b có 1 lựa chọn trong các chữ số 5, 7 do đó có 2 số dạng 0912ab3468.
• 0912ab3486: Các số dạng này giống các số dạng trên nên có 2 số.
• 0912ab3488: Các số dạng này, a có 3 lựa chọn và b có 2 lựa chọn trong các chữ số 5, 6, 7 do đó có 6 số dạng này.
Vậy mạng viễn thông Vinaphone sở hữu tất cả 16 số “đẹp” dạng 0912ab34cd.Câu 63:
 Xem đáp án
Xem đáp án
12 bạn đã làm 10 phút thì phần sân trường chưa quét 12 bạn phải tiếp tục làm trong 20 phút.
Cũng phần sân trường này thì 16 bạn sẽ làm trong số phút là
12 × 20 : 16 = 15 (phút).
Vậy các bạn học sinh tiếp tục làm 15 phút nữa thì quét vệ sinh xong sân trường.Câu 64:
 Xem đáp án
Xem đáp án
Số tiền bộ Lego sau tháng thứ nhất là 1350000 × 0,9 = 1215000 (đồng).
Số tiền bộ Lego sau tháng thứ 2 là 1350000× 0,9 ×0,9 = 1093500(đồng).
Vậy Hùng đợi 2 tháng thì số tiền sẽ đủ mua bộ Lego.Câu 65:
 Xem đáp án
Xem đáp án

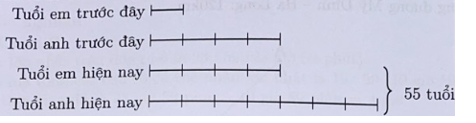
Tuổi em hiện nay là: 22 : (4 + 7) × 4 = 8 (tuổi);
Tuổi anh hiện nay là: 22 – 8 = 14 (tuổi).Câu 66:
 Xem đáp án
Xem đáp án
Viết thêm số A vào bên phải số 1998 ta được số chia hết cho 101.
+) Nếu A là số có 1 chữ số, ta có = (19980+ A) chia hết cho 101.
19980 chia cho 101 dư 83. Muốn chia hết cho 101 thì A chia cho 101 dư 18.
Suy ra A = 18 là số có 2 chữ số (trái với giả thiết).
+) Nếu A là số có 2 chữ số, ta có = (199800 + A) chia hết cho 101.
199800 chia cho 101 dư 22. Muốn chia hết cho 101 thì A chia cho 101 phải dư 79 suy ra A = 79.
Vậy số cần viết là 79.Câu 67:
 Xem đáp án
Xem đáp án
Khi nối các que thì tổng chiều dài của chúng là 1 + 2 + ... + 17 = 153 cm.
Nối tất cả các que thành một hình chữ nhật mà không làm thay đổi hình dạng, kích thước các đoạn thì độ dài các cạnh của hình chữ nhật là số tự nhiên hay tổng chiều dài và chiều rộng là số tự nhiên.
Nửa chu vi hay tổng chiều dài và chiều rộng của hình chữ nhật thể
tạo thành là: .
Do không phải số tự nhiên nên vô lí.
Vậy câu trả lời là không thể.Câu 68:
Cho dãy các hình tam giác theo quy luật như sau:
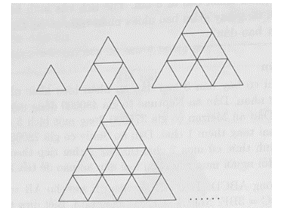
 Xem đáp án
Xem đáp án
Quy luật:
Hình 1: Số hình tam giác là 1 × 1
Hình 2: Số hình tam giác là 2 × 2
Hình 3: Số hình tam giác là 3 × 3
Hình 4: Số hình tam giác là 4 × 4
...
Hình 10: Số hình tam giác là 10 × 10.
Diện tích là 10 × 10 × 0,86 = 86 cm2.Câu 69:
 Xem đáp án
Xem đáp án
Các thừa số của A là các số tự nhiên cách nhau 4 đơn vị.
Ta quan tâm các số chia hết cho 5, 25, 125, 625 trong các thừa số của A.
Trong A có các số chia hết cho 5 là: 20, 40, 60, ... 2020.
Số các số hạng là (2020 – 20) : 20 + 1 = 101.
Trong A có các số chia hết cho 25 là 100, 200, ..., 2000.
Số các số hạng là (2000 – 100) : 100+1 = 20.
Trong A có 4 số chia hết cho 125 là: 500, 1000, 1500, 2000 và trong A không có số nào chia hết cho 625.
Vậy A chứa tất cả 101 + 20 + 4 = 125 thừa số 5.
Dễ thấy trong A chứa nhiều hơn 125 số chẵn nên A có 125 chữ số 0 ở tận cùng.Câu 70:
 Xem đáp án
Xem đáp án
Đổi 20 km/giờ = m/giây.
Trong 3 phút = 180 giây đoàn tàu đi được quãng đường là
× 180 = 1000 (m).
Chiều dài của cây cầu là 1000 – 200 = 800 m.Câu 71:
Bể chứa nước nhà em có vòi bơm nước vào và vòi dẫn nước xuống các phòng sinh hoạt. Chiều cao của bể là 1,8 m, vòi dẫn cách đáy bể 20 cm.
Biết nếu vòi bơm hoạt động liên tục 1 giờ thì bơm được bể, còn vòi dẫn hoạt động liên tục 1 giờ thì xã được bể.
Hỏi nếu lúc đầu bể không có nước mà mở hai vòi cùng hoạt động thì sau bao nhiêu lâu nước đầy bể?

 Xem đáp án
Xem đáp án
Khi vòi bơm vào lượng nước chưa vượt quá vòi dẫn thì vòi dẫn không hoạt động.
Đổi 1,8 m = 180 cm.
Vị trí vòi dẫn cách đáy bể 20cm hay nó cách đáy bể 1 khoảng bể.
Vậy vòi bơm hoạt động một mình trong thời gian là (giờ).
Trong 1 giờ mở cả hai vòi thì lượng nước trong bể tăng lên là (bể)
Vậy thời gian để chảy được bể là (giờ)
Thời gian kể từ lúc mở hai vòi đến khi đầy bể là (giờ).Câu 72:
 Xem đáp án
Xem đáp án
Gọi chiều dài, chiều rộng, chiều cao của hình hộp chữ nhật ban đầu là a, b, c.
Thể tích hình hộp chữ nhật ban đầu là V = a × b × c ;
Thể tích hình hộp chữ nhật lúc sau là
V’ = a × 6 × b × 2× c : 8 = 1,5 × a × b × c = 1,5 × V = 150%V.
Vậy thể tích hình hộp chữ nhật mới tăng 50% so với thể tích hình hộp chữ nhật ban đầu.Câu 73:
Trong siêu thị có bày bán 3 loại dầu ăn nhãn hiệu khác nhau nhưng chất lượng và thể tích như nhau. Dầu ăn Neptune có giá 480000 đồng một bịch 6 chai và đang giảm giá 20%. Dầu ăn Meizan có giá 375000 đồng một bịch 5 chai và đang có khuyến mãi mua 5 chai tặng thêm 1 chai. Dầu ăn Simly có giá 78000 đồng một chai và khuyến mãi với hình thức cứ mua 2 chai thì mỗi 2 chai tiếp theo được giảm giá 30% so với giá gốc. Hỏi người mua nên chọn loại dầu ăn nào để tiết kiệm nhất?
 Xem đáp án
Xem đáp án
Mua dầu ăn Neptune thì 6 chai sẽ hết số tiền là: 480000 × 80% = 384000 (đồng).
Mua dầu ăn Meizan mua 5 chai được tặng 1 chai hết số tiền là 375000 (đồng).
Mua dầu ăn Simly thì mua 2 chai đầu hết 78000 × 2 = 156000 đồng, 4 chai sau hết
156000 × 2 × (100% – 30%) = 218400 (đồng).
Vậy mua 6 chai sẽ hết tất cả 156000 + 218400 = 374400 (đồng)
Vậy người mua nên chọn mua dầu ăn Simly vì giá 6 chai sẽ hết ít tiền nhất.
Câu 75:
Trên bàn có 100 viên kẹo. Trung và Hà chơi một trò chơi theo quy tắc: Mỗi người bốc kẹo một lần rồi đến người kia, số kẹo bốc mỗi lần ít nhất là 1 viên và không vượt quá 3 viên kẹo. Trò chơi kết thúc khi trên bàn hết kẹo và người thắng là người bốc được viên kẹo cuối cùng ở trên bàn. Trung sẽ là người bốc kẹo đầu tiên, bạn hãy chỉ ra một chiến thuật để Trung có bốc thế nào thì Hà cũng là người chiến thắng.
 Xem đáp án
Xem đáp án
Ta quan tâm đến số viên kẹo lấy không vượt quá 3 và ít nhất là 1.
Muốn Hà lúc nào cũng thắng thì anh phải là người lấy kẹo cuối cùng, tức là Trung không lấy được hết số kẹo ở lần áp chót.
Ta đưa ra chiến thuật để cuối cùng đến Trung lấy sẽ còn đúng 4 viên kẹo trên bàn. Nếu Trung bốc k viên thì Hà bốc (4 − k) viên.
Khi đó mỗi lượt chơi số kẹo giảm đi 4 viên. Lại có 100 chia hết cho 4.
Như vậy cuối cùng còn 4 viên, do mỗi người mỗi lần bốc ít nhất là 1 viên và không vượt quá 3 viên kẹo nên Trung không thể bốc hết 4 viên kẹo trên bàn và Hà là người chiến thắng.
Câu 77:
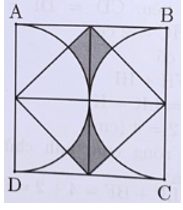
Cho hình vẽ

 Xem đáp án
Xem đáp án
Phần tô màu có diện tích bằng 13 lần diện tích tam giác nhỏ. Toàn bộ hình có 25 tam giác nhỏ.
Diện tích phần tô màu chiếm số phần trăm là 13 : 25 = 0,52 = 52%.Câu 78:
 Xem đáp án
Xem đáp án
Long mua 10 quyển vở và 4 cái bút chì thì số tiền phải trả là
2 × 50000 = 100000 đồng.
Vậy giá tiền 1 quyển vở là
(100000 – 44000) : (10 – 3) = 8000 (đồng).
Ta tính được giá tiền 1 chiếc bút chì là 5000 đồng.
Giá một quyển vở hơn giá một chiếc bút chì là 8000 – 5000 = 3000 (đồng).Câu 79:
 Xem đáp án
Xem đáp án
|
Câu 80:
 Xem đáp án
Xem đáp án
Từ A đến P có 16 chữ cái nên sẽ có 16 hàng ghế.
Hàng ghế A có 20 ghế
Hàng ghế B có 21 ghế
...
Hàng ghế P có 35 ghế
Tổng số ghế là (35 + 20) × 16 : 2 = 440 (ghế).Câu 81:
 Xem đáp án
Xem đáp án
Có 66 số chia hết cho 3 nhỏ hơn 200 là 3, 6, ..., 198.
Tổng các số này là (3 + 198) × 66 : 2 = 6633.
Có 39 số chia hết cho 5 nhỏ hơn 200 là 5, 10, ...,195.
Tổng các số này là (5 + 195) × 39 : 2 = 3900.
Có 13 số chia hết cho cả 3 và 5 là 15, 30, ..., 195.
Tổng các số này là (15 + 195) × 13 : 2 = 1365.
Tổng các số theo yêu cầu đề bài là
6633 + 3900 – 1365 = 9168.Câu 82:
 Xem đáp án
Xem đáp án
Tỉ số tuổi bố hiện nay và hiệu số tuổi là .
Tỉ số tuổi bố 10 năm nữa và hiệu số tuổi là .
Tỉ số tuổi bố hiện nay và tuổi bố 10 năm nữa là .
Tuổi bố hiện nay là 10 : (4 – 3) × 3 = 30 (tuổi);
Tuổi con hiện nay là 30 : 3 = 10 (tuổi);
Tuổi bố hơn tuổi con là 30 – 10 = 20 (tuổi).Câu 83:
 Xem đáp án
Xem đáp án
ST2 = ST1 + 1
ST3 = ST2 + 2
ST4 = ST3 + 3
...
ST40 = ST39 + 39
Cộng theo từng vế và bỏ đi các thành phần giống nhau ta được:
ST40 = ST1 + (1 + 2 + 3 + ... + 39)
ST40 = 3 + (1 + 39) × 39: 2 = 783.Câu 84:
 Xem đáp án
Xem đáp án
Số bé dời dấu phẩy sang phải 2 hàng nên số bé tăng lên 100 lần. Ta có sơ đồ
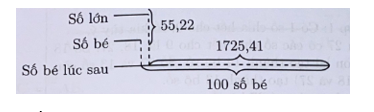
Nhìn vào sơ đồ ta có
1725,41 + 55,22 = 1780,63 chính là 101 lần số bé.
Số bé là 1780,63 : 101 = 17,63;
Số lớn là 55,22 – 17,63 = 37,59.Câu 85:
 Xem đáp án
Xem đáp án
Ban đầu có tối đa 6 đống sỏi.
Ta kí hiệu các con số chỉ số viên sỏi trong mỗi đống.
Ví dụ (1, 1, 2, 2) là có 4 đống sỏi với số sỏi các đống là 1 viên, 1 viên, 2 viên và 2 viên.
•Nếu có 6 đống, mỗi đống 1 viên ta có sơ đồ phép biến đổi như sau
(1, 1, 1, 1, 1, 1) → (6) → (5, 1) → (4, 2) → (3, 1, 2) → (2, 1, 3)
•Nếu có 5 đống
(1, 1, 1, 1, 2) → (5, 1) → (4, 2) → (3, 1, 2) → (2,1,3)
•Nếu có 4 đống
✓ (1, 1, 1, 3,) → (2, 4) → (1, 3, 2)
✓ (1, 1, 2, 2,) → (1, 1, 4)→ (3, 3)→ (2, 2, 2)→ (1, 1, 1, 3)→ (2, 4)→ (1, 3, 2)Câu 86:
 Xem đáp án
Xem đáp án
Cạnh hình lập phương ban đầu là a.
Cạnh hình lập phương lúc sau là 120% × a = 1,2 × a.
Thể tích ban đầu: a × a × a.
Thể tích lúc sau:
a × a × a × 1,2 × 1,2 × 1,2 = a × a × a × 1,728 = a × a × a × 172,8%.
Vậy thể tích hình lập phương tăng lên 172,8% - 100% = 72,8%.Câu 87:
 Xem đáp án
Xem đáp án
Từ 13 đến 27 có 15 số.
Bộ 2 số được chọn xảy ra các trường hợp sau
• Trường hợp 1: Có 1 số chia hết cho 9, số kia tùy ý. Từ 13 đến 27 có các số chia hết cho 9 là: 18, 27. Số 18 và 14 số còn lại tạo thành 14 bộ số. Số 27 và 13 số còn lại (trừ số 18 và 27) tạo thành 13 bộ số.
Vậy trường hợp này có 27 bộ số.
• Trường hợp 2: Có 2 số chia hết cho 3
Từ 13 đến 27 có các số chia hết cho 3 là 15, 18, 21, 24, 27. Vì số 18 và số 27 là những số đã xét ở trường hợp trên nên ta chỉ xét các số chia hết cho 3 khác 18 và 27. Có 3 số là 15, 21, 24. Số 15 tạo với hai số 21 và 24 hai bộ số. Số 21 và số 24 tạo thành 1 bộ số. Vậy trường hợp này có 3 bộ số,
Tất cả có 30 bộ số thỏa mãn đề bài.Câu 88:
Một ô tô đi từ A về B với vận tốc 55 km/giờ. Sau đó một thời gian, một ô tô thứ hai cũng đi từ A về B với vận tốc 62 km/giờ. Như dự định hai ô tô sẽ đến B cùng một lúc, nhưng đi được quãng đường AB thì ô tô thứ nhất giảm vận tốc đi một nửa nên ô tô thứ hai đuổi kịp ô tô thứ nhất cách B 124 km. Tính quãng đường AB.
 Xem đáp án
Xem đáp án
Ta có sơ đồ bài toán như sau:

Ta có AC = AB.
Khi đến C thì ô tô thứ nhất giảm vận tốc đi một nửa, do đó hai xe gặp nhau ở H cách B một khoảng bằng 124 km.
Ô tô thứ hai đi tiếp quãng đường HB hết 124 : 62 = 2 (giờ).
Trong 2 giờ đó ô tô thứ nhất đi đến D, vận tốc bằng vận tốc cũ, do đó quãng đường đi được là
HD = (55 : 2) × 2 = 55 km.
Ta tính được BD = 124 – 55 = 69 km.
Trên quãng đường CB vì vận tốc ô tô thứ nhất giảm một nửa nên quãng đường đi được cũng giảm một nửa. Do đó CD = BD.
Độ dài đoạn BC là 69 × 2 = 138 km.
Vậy quãng đường AB dài 138 × 3 = 414 km.
Đáp số: 414 km.
Câu 90:
Mai chuyển 15 quyển sách từ ngăn 1 sang ngăn II thì thấy tỉ số sách ngăn I và ngăn II là , sau đó Mai lại chuyển 25 quyển sách từ ngăn II sang ngăn I thì thấy tỉ số sách ngăn I và ngăn II là . Tính tổng số sách hai ngăn.
 Xem đáp án
Xem đáp án
Khi chuyển sách qua lại giữa các ngăn thì tổng số sách ở hai ngăn tại mọi thời điểm đều như nhau và bằng tổng số sách hai ngăn lúc chưa chuyển.
Tỉ số sách ngăn I (khi chuyển đi 15 quyển) và tổng số sách hai ngăn là
Tỉ số sách ngăn I (sau khi được nhận 25 quyển sách) và tổng số sách hai ngăn là
Tỉ số sách ngăn I khi chuyển đi 15 quyển và số sách ngăn I sau khi nhận 25 quyển là
Đến đây bài toán về dạng toán hiệu tỉ quen thuộc.
Số sách chênh lệch ở hai ngăn tại hai thời điểm là 25 (quyển).
Số sách ngăn I sau khi chuyển đi 15 quyển là 25 : (3 − 2) × 2 = 50 (quyển).
Số sách của ngăn II sau khi nhận thêm 15 quyển là: (quyển).
Tổng số sách ở hai ngăn là: 105 + 50 = 155 (quyển).
Câu 92:
Tìm số tự nhiên x biết
 Xem đáp án
Xem đáp án
Chọn B
100,1 < 66 + < 111,1
11 × 9,1 < 11 × (6 + x) < 11 × 10,1
9,1 < 6 + x < 10, 1 (cùng giảm đi 11 lần)
6 + 3,1 < 6 + x < 6 + 4,1
3,1 < x < 4,1 (cùng giảm đi 6 đơn vị)
Vậy x = 4.
Câu 93:
Một đội công nhân có 18 người dự định hoàn thành một công việc trong 25 ngày. Sau khi làm được 5 ngày thì đội bổ sung thêm 6 công nhân nữa. Hỏi đội công nhân hoàn thành công việc đó sớm hơn mấy ngày so với dự định? (Biết năng suất làm việc của các công nhân là như nhau)
 Xem đáp án
Xem đáp án
Chọn D
18 người hoàn thành công việc còn lại trong thời gian là 25 – 5 = 20 (ngày)
Số công nhân cả cũ và mới là 18 + 6 = 24 (người)
24 công nhân hoàn thành công việc đó trong số ngày là 18 × 20 : 24 = 15 (ngày)
Đội công nhân đó hoàn thành sớm hơn dự định số ngày là 20 – 15 = 5 (ngày).
Câu 94:
Tổng của hai số ban đầu là 50. Khi gấp số thứ nhất lên 3,5 lần và gấp số thứ hai lên 2,5 lần thì được tổng mới là 145. Tìm hai số đó.
 Xem đáp án
Xem đáp án
Chọn A
2,5 lần tổng của hai số là 50 × 2,5 = 125
Số thứ nhất là 145 – 125 = 20
Số thứ hai là 50 – 20 = 30.
Câu 95:
Chữ số tận cùng của biểu thức sau là chữ số nào?
A = 1 × 2 × 3 × ... × 2019 × 2020 - 1 × 3 × 5 × ... × 2017 × 2019 Xem đáp án
Xem đáp án
A = 1 × 2 × 3 × ... × 2019 × 2020 – 1 × 3 × 5 × ... × 2017 × 2019
Đặt B = 1 × 2 × 3 × ... × 2019 × 2020;
C = 1 × 3 × 5 × ... × 2017 × 2019
Tích B có tận cùng là chữ số 0.
Tích C có tận cùng là chữ số 5.
Vậy A tận cùng là chữ số 5.Câu 96:
 Xem đáp án
Xem đáp án
Khi thêm 2m vào chiều dài và Im vào chiều rộng thì lúc này chiều dài hơn chiều rộng là 7 + 2 −1 = 8 (m)
Chiều rộng hình chữ nhật lúc sau là 8 : (3 – 1) = 4 (m)
Chiều rộng của hình chữ nhật lúc đầu là 4 − 1 =3 (m)
Chiều dài hình chữ nhật ban đầu là 3 + 7 = 10 (m)
Chu vi hình chữ nhật ban đầu là (10 + 3) × 2 = 26 (m)
Diện tích của hình chữ nhật ban đầu là 10 × 3 = 30 (m2).Câu 97:
 Xem đáp án
Xem đáp án
100kg cỏ tươi chứa lượng nước là 100 × 55% = 55 (kg)
Lượng cỏ nguyên chất có trong cỏ tươi cũng như trong có khô không đổi là 100 – 55 = 45 (kg)
Coi lượng cỏ khô là 100% thì tỉ số phần trăm lượng cỏ nguyên chất có trong cỏ khô là 100% – 10% = 90%
Vậy lượng có khô thu được là 45 : 90% × 100% = 50 (kg).Câu 98:
 Xem đáp án
Xem đáp án
60 học sinh nam được chuyển từ trường khác sang tương ứng với
(số học sinh nữ)
Số học sinh nữ của trường tiểu học Thống Nhất là 60 : 3 × 20 = 400 (học sinh).Câu 100:
Cho hình bình hành ABCD có M là trung điểm của cạnh AB. Hai đoạn thẳng AC và DM cắt nhau tại E. Tính diện tích tam giác MEC, biết diện tích/ tam giác MBC = 15 cm2
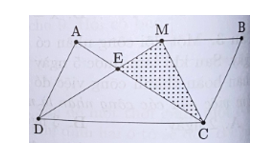
 Xem đáp án
Xem đáp án
Vì M là trung điểm của cạnh AB nên ta có MA = MB.
Hai tam giác CMB và CMA có chung chiều cao kẻ từ C xuống AB và có MA = MB
nên SCMA = SCMB = 15 cm2.
Hai tam giác DAM và MDC có chiều cao bằng nhau (cùng bằng chiều cao hình bình hành) và có DC = AB = 2AM nên SMDC = 2 × SDAM.
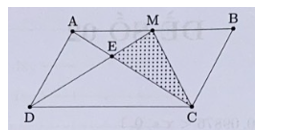
Suy ra chiều cao hạ từ C xuống DM gấp 2 lần chiều cao hạ từ A xuống DM.
Hai tam giác CME và AME có chung cạnh ME và có chiều cao hạ từ C xuống DM gấp 2 lần chiều cao hạ từ A xuống DM, nên SCME = 2SAME (1)
Mặt khác SCME + SAME = SCAM = SCMB = 15 (m2) (2)
Từ (1) (2), áp dụng bài toán tìm hai số khi biết tổng và tỉ số giữa hai số đó, ta có:
Diện tích tam giác MEC là 15 : (1 + 2) × 2 = 10 cm2.
Câu 101:
Tìm các số thập phân x sao cho 0,09876 < x < và x có 3 chữ số ở phần thập phân.
 Xem đáp án
Xem đáp án
Chọn C
0,09876 < x < suy ra 0, 09876 < x < 0,1.
Do đó x = 0,099.
Câu 102:
Có bao nhiêu số có 4 chữ số mà chữ số tận cùng là 5?
 Xem đáp án
Xem đáp án
Chọn D
Gọi số cần tìm có dạng
Chữ số hàng nghìn có 9 cách chọn (khác chữ số 0).
Chữ số hàng trăm có 10 cách chọn.
Chữ số hàng chục có 10 cách chọn.
Theo quy tắc nhân, ta có 9 × 10 × 10 = 900 (số).
Câu 103:
Lớp 5A nếu xếp mỗi bàn 3 học sinh thì 4 học sinh không có chỗ ngồi, còn nếu xếp mỗi bàn 4 học sinh thì còn trống 1 bàn. Hỏi lớp 5A có bao nhiêu học sinh?
 Xem đáp án
Xem đáp án
Chọn B
Nếu xếp mỗi bàn 3 học sinh thì 4 học sinh không có chỗ ngồi, nghĩa là thừa ra 4 học sinh.
Còn nếu xếp mỗi bàn 4 học sinh thì trống 1 bàn, nghĩa là còn thiếu 4 học sinh nữa.
Số bàn của lớp 4A là (4 + 4) : (4 – 3) = 8 (bàn)
Vậy số học sinh của lớp 4A là 8 × 3 + 4 = 28 (học sinh).
Câu 104:
Quyển nhật ký Trái Đất Xanh có 2020 trang. Hỏi cần bao nhiêu chữ số để đánh số trang của quyển nhật ký đó?
 Xem đáp án
Xem đáp án
Chọn B
Từ trang 1 đến trang 9 ta bổ sung mỗi trang thêm 3 chữ số 0.
Từ trang 10 đến trang 99 ta bổ sung mỗi trang 2 chữ số 0. Từ trang 100 đến trang 999 ta bo sung mỗi trang 1 chữ số 0.
Như vậy tất cả các trang ta đều đánh 4 chữ số.
Tổng số chữ số là 2020 × 4 = 8080 (chữ số)
Tổng các chữ số vừa bù vào là 3 × 9 + 2 × 90 + 1 × 900 = 1107 (chữ số)
Số chữ số cần dùng để đánh 2020 trang của quyển nhật ký là 8080 – 1107 = 6973 (chữ số).
Câu 105:
 Xem đáp án
Xem đáp án
Ta vẽ sơ đồ
Câu 106:
 Xem đáp án
Xem đáp án
Thể tích bể nước là 3 × 1,2 × 1,5 = 5,4 (m3)
Đổi: 5,4m3 = 5400 dm3 = 5400 (l)
Lượng nước trong bể hiện có là 5400 × 40 : 100 = 2160 (l)
Lượng nước trong bể sau khi đổ thêm là 5400 × 90 : 100 = 4860 (l)
Lượng nước cần phải đổ thêm là 4860 – 2160 = 2700 (l).Câu 107:
 Xem đáp án
Xem đáp án
Coi số cây đội công nhân phải trồng là 1 đơn vị.
Phân số chỉ số cây ngày thứ hai trồng được là (số cây)
Phân số chỉ số cây ngày thứ ba trồng được là (số cây)
Đội công nhân trồng được số cây là (cây)Câu 108:
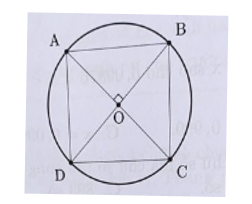
Tìm diện tích hình vuông ABCD, biết hình tròn có diện tích bằng 50,24 cm2.
 Xem đáp án
Xem đáp án
Gọi bán kính của hình tròn tâm O là r.
Ta có: r = OA = OB
Ta có r × r × 3,14 = 50,24
r × r = 50,24: 3,14
r × r = 16
Diện tích tam giác OAB là
SOAB = × OA × OB = × r × r = × 16 = 8 cm2
Vì SABCD = 4 × SOAB nên diện tích hình vuông ABCD là 8 × 4 = 32 cm2.Câu 109:
Một xe khách đi từ Mỹ Đình đến Hạ Long mất 2 giờ. Một xe máy đi từ Hạ Long đến Mỹ Đình mất 3 giờ. Tính quãng đường từ Mỹ Đình đến Hạ Long, biết vận tốc của xe khách hơn vận tốc của xe máy là 20 km/giờ. Nếu hai xe khởi hành cùng một lúc thì chúng gặp nhau tại một địa điểm cách Mỹ Đình bao nhiêu ki-lô-mét?
 Xem đáp án
Xem đáp án
Trên cùng một quãng đường, thời gian và vận tốc là hai đại lượng tỉ lệ nghịch. Ta gọi thời gian xe khách đi từ Mỹ Đình đến Hạ Long là t1, thời gian xe máy đi từ Hạ Long đến Mỹ Đình là t2; vận tốc của xe khách là v1, vận tốc của xe máy là v2.
Ta có . Vận tốc của xe máy là 20 : (3 – 2) × 2 = 40 (km/giờ)
Quãng đường từ Mỹ Đình đến Hạ Long dài là 40 × 3 = 120 (km).
Nếu chia quãng đường ra làm 5 phần, quãng đường xe khách đến địa điểm gặp nhau là 3 phần. Vậy nếu hai xe khởi hành cùng một lúc thì chúng gặp nhau tại địa điểm
cách Mỹ Đình là 120 : 5 × 3 = 72 (km).
Đáp số: Quãng đường Mỹ Đình – Hạ Long: 120 km.
Câu 110:
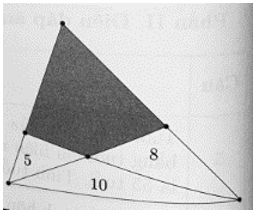
Cho hình vẽ bên, diện tích của ba tam giác lần lượt là 5 cm2, 8 cm2, 10 cm2. Tính diện tích phần tứ giác tô đâm.
 Xem đáp án
Xem đáp án
Đặt tên các điểm như hình vẽ.
Diện tích phần tô đậm cần tính là diện tích của tứ giác AMON.
Ta có mà 2 tam giác này chung đáy BO nên chiều cao hạ từ M xuống BO bằng chiều cao hạ từ C xuống BO.
Tam giác MON và tam giác NOC có chung đáy ON và chiều cao hạ từ M xuống ON bằng chiều cao hạ từ C xuống ON nên .
Suy ra SMON = SNOC = (cm2).
Ta có mà 2 tam giác này có chung đáy CN nên chiều cao hạ từ M xuống CN bằng chiều cao hạ từ B xuống CN.
Tam giác AMC và tam giác ABC có chung đáy AC, chiều cao hạ từ M xuống AC bằng chiều cao hạ từ B xuống AC nên .
Ta có SAMC + SBMC = SABC nên suy ra SBMC = SABC – SAMC = SABC – SABC = SABC.
Do đó SABC = 3SBMC = 3 × (5 + 10) = 45 (cm2).
Diện tích tam giác AMC là (cm2).
Diện tích tứ giác AMON là 30 – 8 = 22 (cm2).
Câu 111:
Một bạn quan sát đồng hồ điện tử có dạng HH:MM (hai chữ số hiển thị giờ, hai chữ số hiển thị phút). Bạn đó lấy hiệu của thời gian lớn nhất có trên đồng hồ với thời gian mà tổng các chữ số có thể nhận là lớn nhất. Biết đồng hồ hiển thị theo dạng 24 giờ từ 00 : 00 đến 23 : 59. Tìm hiệu thời gian đó.
 Xem đáp án
Xem đáp án
Chọn B
Thời gian lớn nhất trên đồng hồ là 23 : 59 (23 giờ 59 phút)
Thời gian mà tổng các chữ số có thể nhận lớn nhất là 19 : 59 (19 giờ 59 phút)
Vậy hiệu thời gian đó là 23 giờ 59 phút – 19 giờ 59 phút = 4 giờ.
Câu 112:
Tìm số tự nhiên nhỏ nhất có 4 chữ số sao cho khi đem số đó chia cho 200 ta được số dư là số dư lớn nhất có thể.
 Xem đáp án
Xem đáp án
Chọn A
Số dư lớn nhất có thể nhỏ hơn số chia 1 đơn vị.
Vậy số dư trong phép chia cho 200 là 199.
Số có 4 chữ số nhỏ nhất chia hết cho 200 là 1000.
Do đó số cần tìm là 1000 +199 = 1199.
Câu 113:
Cứ 3 lít mật ong thì cân nặng 4,2 kg. Mỗi bình thủy tinh cân nặng 0,3 kg thì có thể chứa được 2 lít mật ong. Hỏi 4 bình như thế, mỗi bình chứa 2 lít mật ong cân nặng tất cả bao nhiêu ki-lô-gam?
 Xem đáp án
Xem đáp án
Chọn D
Hai lít mật ong cân nặng là 4,2 : 3 × 2 = 2,8 (kg)
Bình chứa hai lít mật ong cân nặng là 2,8 + 0,3 = 3,1 (kg)
Vậy 4 bình như thế cân nặng là 3,1 × 4 = 12,4 (kg).
Câu 114:
Học sinh khối 6 của trường THCS Cầu Giấy tham gia triển lãm tranh ngoài trời. Nếu chia thành các tổ, mỗi tổ 6 bạn nam và 6 bạn nữ thì còn thừa 20 bạn nam. Nếu chia thành các tổ, mỗi tổ 7 bạn nam và 5 bạn nữ thì thừa 20 bạn nữ. Hỏi khối 6 trường THCS Cầu Giấy có bao nhiêu bạn nam?
 Xem đáp án
Xem đáp án
Chọn D
Nếu chia thành các tổ, mỗi tổ 6 bạn nam và 6 bạn nữ thì còn thừa 20 bạn nam nên số bạn nam nhiều hơn số bạn nữ là 20 bạn.
Nếu chia thành các tổ, mỗi tổ 7 bạn nam và 5 bạn nữ thì còn thừa 20 bạn nữ, do đó nếu ta bớt đi 20 bạn nữ thì số bạn nữ bằng số bạn nam.
Khi đó số bạn nam nhiều hơn số bạn nữ là 20 + 20 = 40 (bạn)
Phân số chỉ 40 bạn là .
Số bạn nam là 40 : 2 × 7 = 140 (bạn).
Câu 115:
 Xem đáp án
Xem đáp án
Coi giá mua chiếc bàn là 100% vậy giá niêm yết là
100% + 20% = 120% (giá mua)
Giá bán chiếc bàn là 120% × 80% = 96% (giá mua)
840 000 đồng tương ứng với 100% – 96% = 4% (giá mua)
Vậy giá mua chiếc bàn là 840000 : 4% = 21000000 (đồng).Câu 116:
 Xem đáp án
Xem đáp án
Vì Chiến có số điểm 10 bằng trung bình cộng của 3 bạn nên số điểm 10 của Chiến cũng bằng trung bình cộng số điểm 10 của An và Bình.
Vậy số điểm 10 của Chiến là (34 + 28) : 2 = 31 (điểm 10)
Nếu Dũng có được 6 điểm 10 nữa thì số điểm 10 của Dũng bằng trung bình cộng số điểm 10 của 3 bạn An, Bình, Chiến. Vậy trung bình cộng số điểm 10 của 4 bạn là (34 + 28 + 31 – 6) : 3 = 29 (điểm 10)
Số điểm 10 của Dũng là 29 – 6 = 23 (điểm 10).Câu 117:
 Xem đáp án
Xem đáp án
Tổng quãng đường hai xe đi kể từ lúc xuất phát cho đến khi vượt qua nhau 70 km là 150 + 70 = 220 (km)
Vì hai xe đi ngược chiều nhau nên trong một giờ cả hai xe đi được quãng đường là 65 + 45 = 110 (km)
Thời gian hai xe vượt qua nhau 70km là 220 :110 = 2 (giờ).Câu 118:
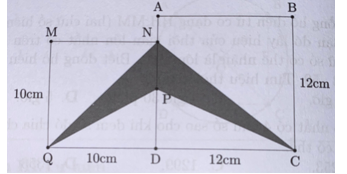
Cho hai hình vuông ABCD và MNDQ lần lượt có cạnh là 12 cm và 10 cm. Nói Q và B, gọi P là giao điểm của QB và AD. Tính diện tích hình tô đậm.
 Xem đáp án
Xem đáp án
Nối N với B và nối P với B.
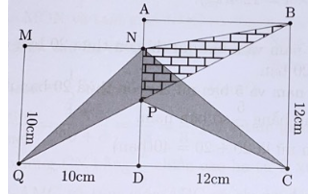
Ta có: SNPB = SNPC (hai tam giác chung đáy NP, chiều cao kẻ từ đỉnh B bằng chiều cao kẻ từ đỉnh C xuống đáy NP).
Vậy phần diện tích tô đậm SNCPQ = SNPQ + SNPB
Ta có: AN = 12 – 10 = 2 (cm); QC = 10 +12 = 22 (cm)
Diện tích hình vuông ABCD là
SABCD = 12 × 12 = 144 (cm2)
Diện tích hình vuông MNDQ là SMNDQ = 10 × 10 = 100 (cm2)
Diện tích tam giác MNQ là SMNQ = 10 × 10 : 2 = 50 (cm2)
Diện tích tam giác ABN là SABN = 12 × 2 : 2 = 12 (cm2)
Diện tích tam giác BQC là SBQC = 22 × 12 : 2 = 132 (cm2)
Vậy phần diện tích tô đậm là
SABCD + SMNDQ – SMNQ – SABN – SQBC = 144 + 100 – 50 –12 – 132 = 50 (cm2)Câu 119:
Hai vòi nước cùng chảy vào bể thì sau 8 giờ bể đầy nước. Nếu chỉ mở vòi A chảy trong 5 giờ rồi khóa lại, sau đó mở vòi B chảy tiếp thì vòi B cần chảy thêm 20 giờ mới đầy bể. Hỏi nếu vòi B chảy một mình thì sau bao lâu sẽ đầy bể?
 Xem đáp án
Xem đáp án
Trong 1 giờ cả hai vòi nước chảy được (bể).
Giả sử vòi A chảy 5 giờ, thì vòi B cũng chảy cùng 5 giờ để hai vòi cùng chảy.
Do đó thời gian của vòi B chảy còn lại là 20 – 5 = 15 (giờ).
Khi mở hai vòi trong 5 giờ thì lượng nước đã đầy được (bể)
Lượng nước còn lại để vòi B chảy tiếp là (bể)
Vòi B chảy 15 giờ được bể, vậy trong 1 giờ vòi B chảy được (bể)
Thời gian vòi B chảy một mình để đầy bể là (giờ)
Đáp số: 40 giờ.
Câu 121:
Tính giá trị biểu thức A = 201,9 × 3,7 + 201,9 × 6,3 − 1,6 × 7,5 + 7,5 × 5,6.
 Xem đáp án
Xem đáp án
Chọn D
A = 201,9 × (3,7 + 6,3) + 7,5 × 5,6 – 7,5 × 1,6
= 201,9 × 10 + 7,5 × (5,6 – 1,6)
A = 2019 + 30 = 2049.
Câu 122:
Có bao nhiêu số có 3 chữ số khác nhau và không có chữ số 5?
 Xem đáp án
Xem đáp án
Chọn A
Gọi số cần tìm có dạng là (a 0; a, b, c ≤ 9).
Hàng trăm có 8 cách chọn (khác 0 và khác 5).
Hàng chục có 8 cách chọn (khác chữ số hàng trăm và khác 5).
Hàng đơn vị có 7 cách chọn (khác chữ số hàng trăm, khác chữ số hàng chục và khác 5).
Theo quy tắc nhân, ta có 8 × 8 × 7 = 448 (số).
Câu 123:
Đội thợ thứ nhất làm đường Trường Chinh dài 3600 m trong 30 ngày. Đội thợ thứ hai làm đoạn đường như thế trong 45 ngày. Hỏi cả hai đội cùng làm việc đó thì mất bao nhiêu ngày?
 Xem đáp án
Xem đáp án
Chọn C
Trong một ngày đội thứ nhất hoàn thành được số mét đường là 3600 : 30 = 120 (m)
Trong một ngày đội thợ thứ hai hoàn thành được số mét đường là 3600 : 45 = 80 (m)
Trong một ngày cả hai đội hoàn thành được số mét đường là 120 + 80 = 200 (m)
Để hoàn thành 3600 mét đường thì cả hai đội phải làm trong số ngày là 3600 : 200 = 18 (ngày).
Câu 124:
Trường tiểu học Newton tuyển sinh bổ sung học sinh khối 4 là 280 em. Trong đó số học sinh nam chiếm 40%. Hỏi nhà trường cần phải tuyển thêm bao nhiêu em để số học sinh nam chiếm 50%?
 Xem đáp án
Xem đáp án
Chọn D
Số em học sinh nam được tuyển sinh bổ sung là 280 × 40 : 100 = 112 (em)
Số học sinh nữ được tuyển bổ sung là 280 – 112 = 168 (em)
Nhà trường cần tuyển thêm số em học sinh nam để tỉ số phần trăm số học sinh nam chiếm 50% là 168 – 112 = 56 (em).
Câu 126:
 Xem đáp án
Xem đáp án
Cách 1
Coi đơn vị không phải ngày mà là buổi (nửa ngày).
Theo đề bài có 15 ngày trời mưa cũng có nghĩa là 15 buổi trời mưa.
Có 12 buổi sáng và 13 buổi chiều trời tạnh tức là có 12 + 13 = 25 buổi trời tạnh.
Số buổi trời tạnh nhiều hơn số buổi trời mưa là 25 – 15= 10 (buổi)
Số ngày trời không mưa (trời tạnh) là 10 : 2 = 5 (ngày)
Số ngày đài quan trắc khí tượng theo dõi là 15 + 5 = 20 (ngày).
Cách 2
Vì 15 ngày trời mưa nên ta có thể giả định đài quan trắc khí tượng theo dõi trong (ít nhất) là 15 ngày.
Khi đó, số buổi trời tạnh là 15, mà theo đề bài số buổi trời tạnh là 25.
Do vậy so với giả định bị thiếu đi 10 buổi hay thiếu 5 ngày.
Vậy số ngày đài quan trắc khí tượng theo dõi là 15 + 5 = 20 (ngày).Câu 127:
 Xem đáp án
Xem đáp án
Tỉ số chiều rộng so với nửa chu vi của hình chữ nhật là
Tỉ số chiều dài so với nửa chu vi của hình chữ nhật là
Tỉ số chiều rộng và chiều dài của hình chữ nhật làCâu 128:
 Xem đáp án
Xem đáp án
Đổi 72km/giờ = 20m/giây.
Đoàn tàu đi qua cầu thì quãng đường bằng tổng chiều dài cây cầu và chiều dài thân tàu.
Vậy tổng quãng đường đoàn tàu đi được là 120 + 1680 = 1800 m
Thời gian tàu đi qua cây cầu Long Biên là 1800 : 20 = 90 (giây).Câu 129:
Một xưởng sản xuất ô tô của hãng xe Vinfast tổng kết cuối năm 2019. Số ô tô của đội Một chiếm tổng số ô tô, đội Hai chiếm , còn lại là số ô tô của đội Ba và đội Bốn. Biết rằng tổng số ô tô của ba đội Hai, Ba và Bốn là 162 chiếc, số ô tô của đội Bốn bằng số ô tô của đội Ba. Tính số ô tô mà đội Ba đạt được trong năm vừa qua.
 Xem đáp án
Xem đáp án
Phân số chỉ số ô tô của đội Hai, Ba và Bốn là (số ô tô)
Do đó tổng số ô tô mà xưởng đó sản xuất được là 162 : 3 × 5 = 270 (chiếc)
Phân số chỉ số ô tô của đội Ba và Bốn là (số ô tô)
Tổng số ô tô của đội Ba và đội Bốn là 270 : 15 × 4 = 72 (chiếc)
Vậy số ô tô đội Ba sản xuất là 72 : (5 + 3) × 5 = 45 (chiếc).
Đáp số: 45 chiếc.
Câu 130:
Cho tam giác ABC, điểm M là điểm chính giữa cạnh BC. Trên cạnh AC lấy điểm N sao cho AN = AC. Nối điểm M với điểm N. MN và AB kéo dài cắt nhau tại điểm P. Cho biết diện tích tam giác APN bằng 10 cm2. Tính diện tích tam giác ABC.
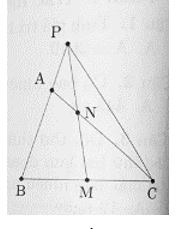
 Xem đáp án
Xem đáp án
Nối B với N ta có ; (vì AN = AC).
Vậy: SPNC = 10 × 3 = 30 (cm2).
Lại có: SBNM = SNMC và SBPM = SPMC (vì đáy BM = MC và chung chiều cao lần lượt kẻ từ đỉnh P và N).
Do đó SBPN = SPNC = 30 (cm2).
Xét tam giác BPN ta có:
SBAN = SBPN – SPAN= 30 – 10 = 20 (cm2). Mà SBAN = SABC
(vì chung chiều cao kẻ từ đỉnh B và đáy AN = × AC).
Từ đó suy ra SABC = 20 × 4 = 80 (cm2).
Đáp số: 80 cm2.
Câu 132:
Một con búp bê được mua về với giá 490000 đồng. Hỏi cần bán búp bê với giá bao nhiêu để lãi 30% giá bán?
 Xem đáp án
Xem đáp án
Chọn D
Đổi 30% giá bán = giá bán.
Để lãi giá bán thì giá bán chính là tiền mua con búp bê. Do đó tương ứng với 490000 đồng. Vậy giá bán con búp bê là 490000 : 7 × 10 = 700000 (đồng).
Câu 133:
Tìm biết = × 3 + 3,4
 Xem đáp án
Xem đáp án
Chọn B
Nhân cả hai vế với 10, ta có
= × 3 + 34
a × 10 + b = (b × 10 + a) × 3 + 34
a × 10+ b = b × 30 + a × 3 + 34
a × 7 = b × 29 + 34.
Vì a lớn nhất là 9 nên b × 29 + 34 lớn nhất là 9 × 7 = 63 do đó b chỉ có thể bằng 0 hoặc 1. Thử chọn ta được b = 1, a = 9. Vậy số cần tìm là 91.
Câu 134:
Tổng của hai số tự nhiên bằng 2020. Nếu viết thêm một chữ số vào bên phải số hạng thứ nhất và giữ nguyên số hạng thứ hai thì ta được tổng mới bằng 3000. Tìm hai số đã cho.
 Xem đáp án
Xem đáp án
Chọn D
Ta có sơ đồ sau.

Khi viết thêm 1 chữ số a vào bên phải thì số hạng thứ nhất gấp lên 10 lần và cộng thêm a đơn vị.
9 lần số hạng thứ nhất và số a có tổng là 3000 – 2020 = 980
Vì 980 : 9 = 108 dư 8 nên chữ số cần viết thêm là 8.
Vậy số hạng thứ nhất là 108; Số hạng thứ hai là 2020 – 108 = 1912.
Câu 135:
 Xem đáp án
Xem đáp án
Sau khi Thanh giảm đi 120 con tem và Loan tăng 200 con tem thì lúc này số tem của Loan nhiều hơn số tem của Thanh là
120 – 100 + 200 = 220 (con tem)
Số tem của Thanh lúc sau là 220 : (3 – 1) = 110 (con tem)
Số tem của Thanh lúc đầu là 110 + 120 = 230 (con tem)
Số tem của Loan lúc đầu là 230 – 100 = 130 (con tem)
Tổng số tem của hai bạn lúc ban đầu là 230 + 130 = 360 (con tem).Câu 137:
 Xem đáp án
Xem đáp án
Phân số chỉ chiều dài còn lại là (chiều dài)
Phân số chỉ chiều rộng còn lại là (chiều rộng)
Ta có chiều dài bằng chiều rộng, coi chiều dài là 7 phần thì chiều rộng là 6 phần.
Chiều dài của mảnh đất là 20 : (7 – 6) × 7 = 140 (m)
Chiều rộng của mảnh đất là 140 – 20 = 120 (m)
Diện tích của mảnh đất là 140 × 120 = 16800 (m2).Câu 138:
 Xem đáp án
Xem đáp án
Nối B với D.
Diện tích hình thang vuông ABCD là (12 + 6) × 8 : 2 =72 (cm2).
Vì cạnh BE chia hình thang ra thành 2 nửa có diện tích bằng nhau nên diện tích tam giác BEC là 72 : 2 = 36 (cm2)
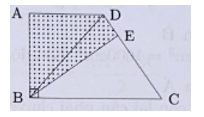
Xét tứ giác ABED ta có: SBED = SABED – SABD
Ta có SABD = 6 × 8 : 2 = 24 (cm2)
Từ đó suy ra SBED = 36 – 24 = 12 (cm2)
Ta có và hai tam giác này có chung chiều cao hạ từ B nên
Câu 139:
Lớp 5A cử một số bạn tham gia cuộc thi “Trạng Nguyên Nhỏ Tuổi”. Số học sinh còn lại của lớp nhiều hơn số học sinh cả lớp là 8 em. Nếu số em tham gia cuộc thi bớt đi 2 em thì số học sinh tham gia bằng số học sinh của cả lớp. Tính số em học sinh tham gia cuộc thi “Trạng Nguyên Nhỏ Tuổi”.
 Xem đáp án
Xem đáp án
Nếu lớp bớt đi 2 em tham gia cuộc thi thì số học sinh còn lại sẽ tăng thêm 2 em và nhiều hơn số học sinh của lớp là 8 + 2 = 10 (học sinh)
Phân số chỉ số học sinh còn lại của lớp là (số học sinh cả lớp)
Phân số chỉ 8 học sinh là (số học sinh cả lớp)
Vậy số học sinh cả lớp là 10 : 1 × 4 = 40 (học sinh).
Số học sinh tham gia cuộc thi Trạng Nguyên Nhỏ Tuổi là 40 : 4 + 2 = 12 (học sinh).
Đáp số: 12 học sinh.
Câu 140:
Một ô tô đi từ Thanh Hóa lúc 7 giờ và dự kiến đến Hà Nội lúc 11 giờ 30 phút với vận tốc 64km/giờ. Nhưng thực tế đến 9 giờ 30 phút ô tô đã đi được 150 km.
Hỏi:
a) Từ 7 giờ đến 9 giờ 30 phút, ô tô đã đi với vận tốc bao nhiêu km/giờ?
b) Để đến B đúng dự định, ô tô phải đi đoạn đường còn lại với vận tốc bao nhiêu km/giờ?
 Xem đáp án
Xem đáp án
a) Thời gian từ 7 giờ đến 11 giờ 30 phút là
11 giờ 30 phút – 7 giờ = 4 giờ 30 phút = 4,5 giờ.
Thời gian từ 7 giờ đến 9 giờ 30 phút là
9 giờ 30 phút – 7 giờ = 2 giờ 30 phút = 2,5 giờ.
Từ 7 giờ đến 9 giờ 30 phút ô tô đã đi với vận tốc là 150 : 2,5 = 60 (km/giờ).
b) Đoạn đường xe ô tô đi từ Thanh Hóa đến Hà Nội dài là 64 × 4, 5 = 288 (km).
Đoạn đường còn lại dài là 288 – 150 = 138 (km).
Thời gian từ 9 giờ 30 phút đến 11 giờ 30 phút là
11 giờ 30 phút – 9 giờ 30 phút = 2 giờ.
Ô tô phải đi đoạn đường còn lại với vận tốc là 138 : 2 = 69 (km/giờ).
Đáp số:
a) 60 km/giờ
b) 69 km/giờ.
Câu 141:
1 lít gấp 25 cm3 số lần là:
 Xem đáp án
Xem đáp án
Chọn B
Đổi 1 lít = 1dm3 = 1000 cm3. Khi đó 1000 : 25 = 40 (lần)
Câu 142:
Trong đợt cứu trợ người dân miền Nam do ảnh hưởng của dịch Covid-19, ban tổ chức đã quyên góp được 100 tấn lương thực. Để chở hết số lương thực vào thành phố Hồ Chí Minh ban tổ chức chia các ngày để chở hết số lương thực. Ngày thứ nhất, để chở 36 tấn lương thực cần 6 xe ô tô. Ngày thứ hai thì cần bao nhiêu xe ô tô cùng loại để chở hết số lương thực còn lại?
 Xem đáp án
Xem đáp án
Chọn A
Số lương thực còn lại cần phải chuyển là 100 – 36 = 64 (tấn).
Một xe chở được số tấn là 36 : 6 = 6 (tấn).
Ta có 64 : 6 = 10 (dư 4).
Vậy cần số xe để chở hết số lương thực còn lại là 10 + 1 = 11 (xe).
Câu 143:
Một bể nước dạng hình hộp chữ nhật có kích thước đo trong lòng bể là dài 4 (m), rộng 3 (m), cao 1,5 (m). Một vòi nước chảy vào bể 1 phút được 20 lít (1 dm3 =1 lít). Thời gian để vòi chảy đầy bể là bao lâu?
 Xem đáp án
Xem đáp án
Chọn D
Bể chứa được lượng nước là 4 × 3 × 1, 5 = 18 (m3) = 18000 dm3.
Một giờ vòi chảy được lượng nước là 20 × 60 = 1200 (lít) = 1200dm3.
Vậy cần số giờ để vòi chảy đầy bể là 18000 : 1200 = 15 (giờ)
Câu 144:
 Xem đáp án
Xem đáp án
Câu 145:
 Xem đáp án
Xem đáp án
Câu 146:
 Xem đáp án
Xem đáp án
Số khẩu trang và kính chống giọt bắn là
1000000 – 450000 – 250000 = 300000.
Số khẩu trang còn lại sau khi bán là 300000 : 20 × 17 = 255000 (chiếc)
Vậy số khẩu trang lúc đầu là 450000 + 255000 = 705000 (chiếc)Câu 147:
Cho hình bình hành ABCD. Trên cạnh AB lấy điểm P, trên cạnh DC lấy điểm Q sao cho AP = DQ. H và K là hai điểm nằm trên BC và AD. Tính diện tích tứ giác KPHQ, biết diện tích hình bình hành ABCD là 48 cm2.
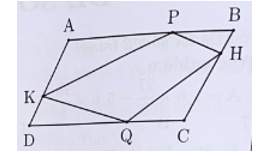
 Xem đáp án
Xem đáp án
Gọi AH là đường cao (H thuộc DC). Khi đó tổng chiều cao kẻ từ K xuống AB và CD bằng AH; và ta cũng có tổng chiều cao kẻ từ H xuống AB và CD bằng AH. Do đó
SKHPQ = SABCD – (SAKP + SPBH + SKDQ + SQCH).
Khi đó SAPK + SKDQ = , SPBH + SQHC =
Vậy tổng 4 tam giác nhỏ là
Khi đó diện tích tứ giác cần tính là
SKHPQ = SABCD – × AH × CD = AH × CD – × AH × CD = × AH × CD
= × 48 = 24Câu 148:
Một ca nô xuất phát lúc 6 giờ 25 phút xuôi dòng từ A đến B với vận tốc 27 km/giờ. Khi đi đến B thì ca nô nghỉ 1 giờ 30 phút, sau đó đi ngược dòng từ B về A với vận tốc 21 km/giờ và đến B lúc 16 giờ kém 5 phút cùng ngày. Hỏi:
a) Ca nô đã đi trong bao lâu (không kể thời gian nghỉ)?
b) Khúc sông từ A đến B dài bao nhiêu?
 Xem đáp án
Xem đáp án
a. Đổi 16 giờ kém 5 phút = 15 giờ 55 phút
Thời gian ca nô đã đi không kể thời gian nghỉ là:
15 giờ 55 phút – 6 giờ 25 phút – 1 giờ 30 phút = 8 (giờ)
b. Tỉ số vận tốc khi xuôi dòng từ A đến B so với vận tốc khi ngược dòng từ B về A là:
Do quãng đường xuôi dòng và ngược dòng là như nhau nên vận tốc và thời gian là hai đại lượng tỉ lệ nghịch. Vậy tỉ số thời gian xuôi dòng và thời gian ngược dòng là .
Thời gian ca nô đi xuôi dòng là: 8 : (7 + 9) × 7 = 3,5 (giờ)
Khúc sông AB dài là: 3,5 × 27 = 94,5 (km)
Đáp số: a. 8 giờ; b. 94,5km
Câu 149:
Thầy Đông cho học sinh của mình chơi một trò chơi. Thầy có 3 hộp bi A, B và C lần lượt có 5, 12 và 16 viên bi. Luật của trò chơi như sau: ta lấy từ 2 hộp bắt kỳ một viên bi rồi bỏ vào hộp còn lại. Thầy yêu cầu qua 3 lượt bắc thì cuối cùng hộp A, B, C sẽ có lần lượt 7, 8 và 18 viên bi.
1. Điền tiếp vào bảng số lượng bi của mỗi hộp A, B, C sau các lượt bốc:
|
|
Hộp A |
Hộp B |
Hộp C |
|
|
5 |
12 |
16 |
|
Lượt 1 |
4 |
11 |
16 |
|
Lượt 2 |
|
|
|
|
Lượt 3 |
|
|
|
|
Cuối cùng |
7 |
8 |
18 |
2. Lần tiếp theo thầy Đông yêu cầu cuối cùng mỗi hộp phải có 11 viên bi. Sau nhiều lần thử, một bạn học sinh nhận xét rằng “Sau một lần chuyển thì số bi mỗi hộp khi chia cho 3 sẽ có dư khác nhau”. Hãy chứng minh rằng bạn học sinh này đúng và qua đó xét xem yêu cầu của thầy Đông có thực hiện được hay không?
 Xem đáp án
Xem đáp án
|
|
Hộp A |
Hộp B |
Hộp C |
|
|
5 |
12 |
16 |
|
Lượt 1 |
4 |
11 |
16 |
|
Lượt 2 |
6 |
10 |
17 |
|
Lượt 3 |
8 |
9 |
16 |
|
Cuối cùng |
7 |
8 |
18 |
2. Tại thời điểm lúc đầu 5; 12; 16 thì 12 chia hết cho 3; 16 chia 3 dư 1 và 5 chia 3 dư 2.
Giả sử bạn học sinh đó nói đúng, tại một thời điểm bất kì nào đó ta có bộ ba số số viên bi trong các hộp A, B, C là a, b, c với a chia hết cho 3, b chia 3 dư 1 và c chia 3 dư 2. Ta xét 3 trường hợp:
+) TH1: a bớt 1, b bớt 1 và c thêm 2
Khi đó (a − 1) chia cho 3 dư 2, (b − 1) chia hết cho 3 và (c + 2) chia cho 3 dư 2. Do đó, bộ 3 số mới cũng đúng với nhận xét.
+) TH2: a bớt 1, c bớt 1 và b thêm 2.
Khi đó (a – 1) chia cho 3 dư 2, (b + 2) chia hết cho 3 và (c − 1) chia cho 3 dư 1.
+) TH3: b bớt 1, c bớt 1 và a thêm 2
Khi đó, (a + 1) chia cho 3 dư 2, (b − 1) chia hết cho 3 và (c − 1) chia cho 3 dư 1.
Do đó, bộ ba số mới cũng đúng với nhận xét
- Như vậy, ở tất cả các trường hợp thì đều có bộ 3 số mới chia cho 3 có số dư khác nhau.
Do vậy, bạn học sinh nhận xét đúng.
- Vì bạn học sinh đó nhận xét đúng nên yêu cầu cuối cùng của thầy Đông không thực hiện được vì khi cả 3 hộp có 11 viên bi thì số dư các hộp là không giống nhau.
Do vậy, yêu cầu cuối cùng của thầy Đông là sai.
Câu 150:
Trong một đợt giảm giá, tất cả sản phẩm được giảm giá so với giá gốc. Chị Yến mua 1 chiếc váy, 1 chiếc áo và 1 đôi giày có giá gốc như bảng sau
|
Váy |
Áo |
Giày |
|
280 000 đồng |
170 000 đồng |
240 000 đồng |
Hỏi chị Yến phải trả tổng cộng bao nhiêu tiền?
 Xem đáp án
Xem đáp án
Đáp án C.
Số tiền phải trả bằng (giá gốc).
Số tiền chị Yến phải trả là (280000 + 170000 + 240000) : 3 × 2 = 460000 (đồng).
Câu 151:
Sân trường Nguyễn Tất Thành có chu vi là 142 m. Các bạn học sinh lớp 5A1 làm mô hình trường với tỉ lệ 1 : 100. Hỏi sân trường ở mô hình có chu vi bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án B.
Chu vi có số đo là đơn vị đo độ dài nên tỉ lệ của nó trên bản đồ cũng bằng tỉ lệ của chiều dài, chiều rộng. Sân trường Nguyễn Tất Thành ở bản mô hình có chu vi là 142 : 100 = 1,42(m).
Câu 152:
Cách đây 6 năm, tuổi mẹ hơn tuổi con là 30 tuổi. Hiện nay, tổng số tuổi của hai mẹ con là 54 tuổi. Hỏi hiện nay con bao nhiêu tuổi?
 Xem đáp án
Xem đáp án
Đáp án C.
Hiệu số tuổi của hai mẹ con luôn không đổi là 30 tuổi.
Hiện nay tổng số tuổi của hai mẹ con là 54 tuổi.
Tuổi con hiện nay là (54 – 30) : 2 = 12 (tuổi).
Câu 153:
Trong buổi triển lãm tranh và đấu giá từ thiện của một họa sĩ nhí, một bức tranh được đưa ra đấu giá với giá khởi điểm là 550 000 đồng. Người thứ nhất trả giá cao hơn giá khởi điểm 10%. Người thứ hai trả giá cao hơn giá người thứ nhất đưa ra là 10%. Người thứ ba đưa ra giá cao hơn giá của người thứ hai là 100 000 đồng và đã mua được bức tranh đó. Hỏi bức tranh được bán với giá bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án D.
Giá người thứ nhất đưa ra là 550000 : 100 × (100 + 10) = 605 000 (đồng);
Giá người thứ hai đưa ra là 605 000 : 100 × (100 + 10) = 665 500 (đồng);
Giá người thứ ba đưa ra hay giá của bức tranh là 665 500+100 000 = 765 500 (đồng).
Câu 154:
 Xem đáp án
Xem đáp án
Thứ tự các viên bi được lặp lại theo nhóm 4 màu: đỏ, xanh, vàng, trắng.
Ta có 2020 : 4 = 505 (nhóm). Viên bi thứ 2020 là viên cuối cùng trong nhóm thứ 505.
Vậy viên bi thứ 2020 có màu trắng.Câu 155:
 Xem đáp án
Xem đáp án
Câu 156:
 Xem đáp án
Xem đáp án
Quãng đường đi từ nhà đến trường bằng quãng đường đi từ trường về nhà. Bạn Nam đi đến trường quãng đường 1 km hết giờ, đi từ trường về nhà quãng đường 1 km hết giờ.
Vận tốc trung bình trên 1 km đi và về bằng vận tốc trung bình của Nam trên cả 2 đoạn đường và bằng (km/giờ).Câu 157:
 Xem đáp án
Xem đáp án
Một năm có 12 tháng, mỗi tháng có 12 ngày liên tiếp từ mùng 1 đến 12 có thể giao hoán thứ tự ghi số chỉ ngày và chỉ tháng tạo ra hiểu nhầm. Tuy nhiên, có 12 ngày trong năm có số chỉ ngày và tháng trùng nhau nên không gây ra cách hiểu nhầm khi đảo thứ tự (1/1; 2/2; 3/3;..; 11/11; 12/12).
Vậy tổng số ngày trong năm có thể gây ra cách hiểu nhầm là
12 × 12 − 12 = 132 (ngày).Câu 158:
Minh và Linh cùng sưu tập tem. Nếu Minh cho Linh 12 con tem thì số tem của Minh bằng số tem của Linh. Nếu Linh cho Minh 30 con tem thì số tem của Linh bằng số tem của Minh. Tính số tem của mỗi bạn.
 Xem đáp án
Xem đáp án
Khi cho nhau tem thì tổng số tem của cả hai bạn không đổi.
Minh cho Linh 12 con tem thì số tem của Minh bằng số tem của Linh hay bằng tổng số tem.
Linh cho Minh 30 con tem thì số tem của Minh bằng 5 lần số tem Linh hay bằng tổng số tem.
Số tem của Minh tại hai thời điểm chênh lệch nhau là 12 + 30 = 42 (tem).
Tổng số tem không đổi nên 42 tem ứng với (tổng số tem)
Tổng số tem của hai bạn là 42 × 2 = 84 (tem).
Số tem của Minh là 84 : (1 + 2) × 1 + 12 = 40 (tem).
Số tem của Linh là 84 – 40 = 44 (tem).
Đáp số : Minh có 40 con tem; Linh có 44 con tem.