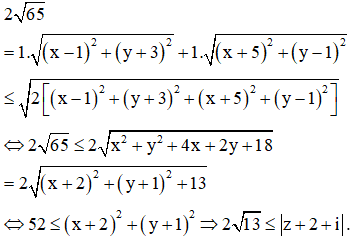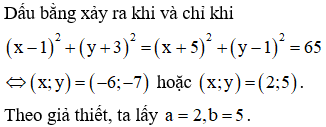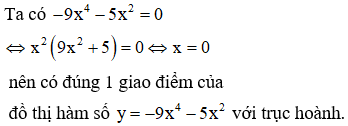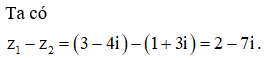50 câu hỏi trắc nghiệm thuộc Đề thi thử THPTQG môn Toán cực hay có lời giải chi tiết (Đề 22)

Câu 1:

Trong không gian Oxyz, cho mặt phẳng $(P) : 2 x - 3 y + z - 10 = 0$ . Điểm nào dưới đây thuộc mặt phẳng $(P)$ ?

A. $M_{1} (2; 1; 2)$

B. $M_{2} (2; 2; 0)$

C. $M_{3} (1; 2; 0)$

D. $M_{4} (2; - 2; 0)$

Xem đáp án

Chọn đáp án D.

Câu 2:

Số giao điểm của đồ thị hàm số $y = - 9 x^{4} - 5 x^{2}$ với trục hoành là

A. 3

B. 0

C. 1

D. 4

Xem đáp án

Chọn đáp án C.

Câu 3:

Nghiệm của phương trình $\log_{2019} (x - 5) = 13$ là

A. $x = 2019^{13} + 5$

B. $x = 13^{2019} - 5$

C. $x = 2019^{13} - 5$

D. $x = 13^{2019} + 5$

Xem đáp án

Chọn đáp án A.

Câu 4:

Cho hai số phức $z_{1} = 3 - 4 i$ và $z_{2} = 1 + 3 i$ . Hiệu số phức $z_{1}$ và $z_{2}$ bằng

A. 4 - i

B. 2 - 7i

C. 2 - i

D. 4 - 7i

Xem đáp án

Chọn đáp án B.

Câu 5:

Tìm tập xác định của hàm số $y = {(x^{2} - 2 x - 8)}^{\sqrt{3}}$

A. $ℝ$

B. $(- \infty; - 2] \cup [4; + \infty)$

C. $ℝ \ \{- 2; 4\}$

D. $(- \infty; - 2) \cup (4; + \infty)$

Xem đáp án

Chọn đáp án D.

Câu 6:

Cho hàm số $y = f (x)$ liên tục trên $ℝ$ và có bảng biến thiên như hình dưới đây:

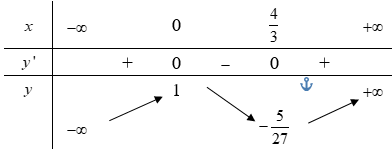
Mệnh đề nào dưới đây đúng?

A. Hàm số đạt cực đại tại $x = 1$

B. Hàm số đạt cực đại bằng 1.

C. Hàm số đạt cực tiểu bằng $\frac{4}{3}$

D. Hàm số đạt cực tiểu tại $x = - \frac{5}{27}$

Xem đáp án

Chọn đáp án B.

Câu 7:

Khối trụ có bán kính đáy là r và độ dài chiều cao là h có thể tích bằng

A. $2 {πr}^{2} h$

B. ${πr}^{2} h$

C. $\frac{1}{3} {πr}^{2} h$

D. ${πr}^{2} h$

Xem đáp án

Chọn đáp án D.

Câu 8:

Cho cấp số nhân $(a_{n})$ có số hạng đầu bằng 3 và công bội $q = 2$ . Giá trị của $a_{5}$ bằng

A. 96

B. 48

C. 13

D. 11

Xem đáp án

Chọn đáp án B.

Câu 9:

Họ nguyên hàm của hàm số $f (x) = 5 x^{4} - e^{x}$ là

A. $20 x^{3} - e^{x} + C$

B. $x^{5} - \frac{1}{x + 1} e^{x + 1} + C$

C. $20 x^{3} - x e^{x - 1} + C$

D. $x^{5} - e^{x} + C$

Xem đáp án

Chọn đáp án D.

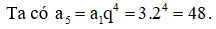
Câu 10:

Trong không gian Oxyz, cho điểm $M (- 3; 9; 6)$ . Gọi $M_{1}, M_{2}, M_{3}$ lần lượt là hình chiếu vuông góc của M trên các trục tọa độ Ox, Oy, Oz. Mặt phẳng $M_{1} M_{2} M_{3}$ có phương trình là

A. $\frac{x}{- 3} + \frac{y}{9} + \frac{z}{6} = 0$

B. $\frac{x}{3} + \frac{y}{- 9} + \frac{z}{- 6} = 1$

C. $\frac{x}{- 3} + \frac{y}{9} + \frac{z}{6} = 1$

D. $\frac{x}{- 1} + \frac{y}{3} + \frac{z}{2} = 1$

Xem đáp án

Chọn đáp án C.

Câu 11:

Biết rằng $4^{a} = x$ và $16^{b} = y$ . Khi đó xy bằng

A. $64^{a b}$

B. $4^{a + 2 b}$

C. $4^{2 a b}$

D. $16^{a + 2 b}$

Xem đáp án

Chọn đáp án B.

Câu 12:

Cho $\int_{0}^{4} f (x) d x = 2018$ . Giá trị $\int_{0}^{2} f (2 x) d x + \int_{- 2}^{2} f (2 - x) d x$ bằng

A. 4036

B. 3027

C. 0

D. -1009

Xem đáp án

Chọn đáp án B.

Câu 13:

Cho hình hộp chữ nhật $A B C D . A' B' C' D'$ có $A B = a \sqrt{3}$ và $A D = a$ (tham khảo hình vẽ). Góc giữa hai đường thẳng $B' D'$ và AC bằng

A. $90 °$

B. $30 °$

C. $45 °$

D. $60 °$

Xem đáp án

Chọn đáp án D.

Gọi O là tâm của hình chữ nhật ABCD

Câu 14:

Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?

A. $y = x^{4} - 2 x^{2}$

B. $y = \frac{2 x + 1}{x - 1}$

C. $y = - x^{3} + 3 x$

D. $y = 2 x^{2} - x^{4}$

Xem đáp án

Chọn đáp án D.

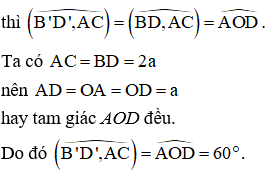
Câu 15:

Trong không gian Oxyz, cho điểm $I (2; 5; 3)$ và đường thẳng $d : \frac{x - 1}{2} = \frac{y}{1} = \frac{z - 2}{2}$ . Đường thẳng Δ đi qua I và vuông góc với hai đường thẳng OI, d có phương trình là

A. $\frac{x + 2}{7} = \frac{y + 5}{- 2} = \frac{z + 3}{- 8}$

B. $\frac{x - 2}{- 8} = \frac{y - 5}{7} = \frac{z - 3}{- 2}$

C. $\frac{x + 2}{7} = \frac{y + 5}{2} = \frac{z + 3}{- 8}$

D. $\frac{x - 2}{7} = \frac{y - 5}{2} = \frac{z - 3}{- 8}$

Xem đáp án

Chọn đáp án D.

Cách 2: Nhận thấy tọa độ điểm I không thỏa mãn phương trình ở phương án A và phương án C nên loại hai phương án này.

d có một vectơ chỉ phương là

Đường thẳng có phương trình trong phương án B có vectơ chỉ phương

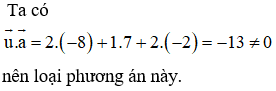
Câu 16:

Giá trị nhỏ nhất của hàm số $f (x) = \frac{x^{2} + 3}{x - 1}$ trên $[2; 4]$ bằng

A. 6

B. $\frac{19}{3}$

C. 2

D. 7

Xem đáp án

Chọn đáp án A.

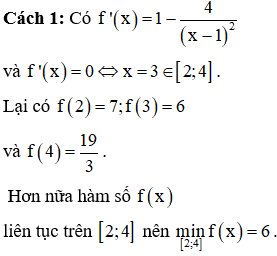
nên ta kiểm tra từng phương án từ nhỏ đến lớn để tìm phương án đúng.

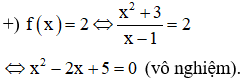
Vậy giá trị nhỏ nhất không phải bằng 2. Do đó loại phương án C.

Câu 17:

Tìm các số thực p và q thỏa mãn $3 p + (2 q - 3 i) = 9 - 8 i$ với i là đơn vị ảo.

A. $p = 2, q = - 4$

B. $p = 3, q = - \frac{5}{2}$

C. $p = 4, q = - 4$

D. $p = 3, q = - \frac{11}{2}$

Xem đáp án

Chọn đáp án A.

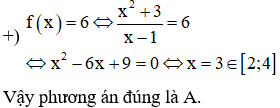
Câu 18:

Đồ thị hàm số $y = \frac{6 x^{2} - 5 x + 1}{2 x^{2} + 9 x - 5}$ có bao nhiêu đường tiệm cận đứng và tiệm cận ngang?

A. 2

B. 3

C. 4

D. 1

Xem đáp án

Chọn đáp án A.

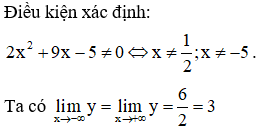
nên đồ thị có một tiệm cận ngang là y = 3.

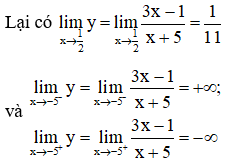
nên đồ thị có một tiệm cận đứng là x = -5. Vậy đồ thị hàm số có tất cả 2 đường tiệm cận, trong đó có một tiệm cận đứng và một tiệm cận ngang.

Câu 19:

$\underset{x \to 0}{l i m} \frac{\cos (3 x) - 1}{x^{2}}$ bằng

A. $\frac{9}{2}$

B. $- \frac{3}{2}$

C. $- \frac{2}{3}$

D. $- \frac{9}{2}$

Xem đáp án

Chọn đáp án D.

Cách 1: (Sử dụng giới hạn cơ bản)

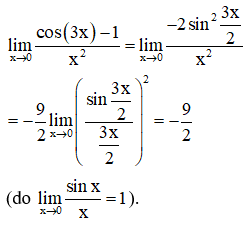
Cách 2: (Sử dụng quy tắc Lopital)

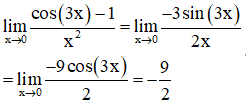
Câu 20:

Trong không gian Oxyz, cho hai mặt phẳng $(P) : 2 x - y + 2 z - 4 = 0$ và $(Q) : 2 x - y + 2 z + 5 = 0$ . Mặt cầu $(S)$ tiếp xúc với hai mặt phẳng $(P)$ và $(Q)$ có bán kính bằng

A. 3

B. $\frac{3}{2}$

C. 9

D. $\frac{1}{2}$

Xem đáp án

Chọn đáp án B.

Câu 21:

Nghiệm của phương trình $2 \sin x + \sqrt{3} = 0$ là

A. $x = \pm \frac{2 π}{3} + k 2 π, k \in ℤ$

B. $x = \pm \frac{5 π}{6} + k 2 π, k \in ℤ$

C. $x = - \frac{π}{3} + k 2 π hoặc x = \frac{4 π}{3} + k 2 π; k \in ℤ$

D. $x = - \frac{π}{6} + k 2 π hoặc x = \frac{7 π}{6} + k 2 π; k \in ℤ$

Xem đáp án

Chọn đáp án C.

Câu 22:

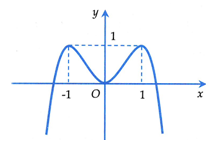
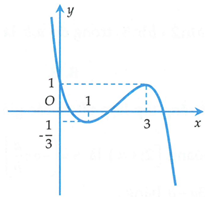
Cho hàm số $y = f (x)$ có đạo hàm trên R và đồ thị hàm số $y = f' (x)$ như hình bên. Số điểm cực trị của hàm số $g (x) = 2019 f () - 2018 x + 13$ là

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Chọn đáp án D.

Câu 23:

Biết rằng khối tứ diện đều cạnh bằng k thì có thể tích bằng $\frac{\sqrt{2} k^{3}}{12}$ . Cho hình lập phương $A B C D . A' B' C' D'$ có cạnh bằng $a \sqrt{2}$ . Tính theo a thể tích khối tứ diện $A C B' D'$ .

A. $\frac{2 \sqrt{2} a^{3}}{3}$

B. $\frac{\sqrt{2} a^{3}}{6}$

C. $\frac{\sqrt{2} a^{3}}{2}$

D. $\frac{a^{3}}{3}$

Xem đáp án

Chọn đáp án A.

Chú ý: Tứ diện đều chỉ là trường hợp đặc biệt của một số tứ diện hoặc một hình chóp tam giác. Chúng ta có các kết quả như sau:

1. Cho khối chóp tam giác đều có cạnh đáy bằng a và cạnh bên bằng b. Thể tích khối chóp tam giác đều bằng

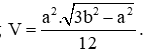
2. Cho khối tứ diện ABCD có và các cạnh còn lại đều bằng a. Thể tích khối tứ diện ABCD là

3. Cho khối tứ diện ABCD có AB = x, CD = y và các cạnh còn lại đều bằng a. Thể tích khối tứ diện ABCD là

4. Cho khối tứ diện gần đều ABCD có AB = CD = a, AC = BD = b, AD = BC = c. Thể tích khối tứ diện ABCD là

Câu 24:

Biết rằng phương trình $(z + 3) (z^{2} - 2 z + 10) = 0$ có ba nghiệm phức $z_{1}, z_{2}, z_{3}$ là . Giá trị của $|z_{1}| + |z_{2}| + |z_{3}|$ bằng

A. 5

B. 23

C. $3 + 2 \sqrt{10}$

D. $3 + \sqrt{10}$

Xem đáp án

Chọn đáp án C.

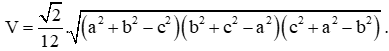
Câu 25:

Giả sử rằng f là hàm số liên tục và thỏa mãn $3 x^{5} + 96 = \int_{c}^{x} f (t) d t$ với mỗi $x \in ℝ$ , trong đó c là một hằng số. Giá trị của c thuộc khoảng nào trong các khoảng dưới đây?

A. (-97;-95)

B. (-3;-1)

C. (14;16)

D. (3;5)

Xem đáp án

Chọn đáp án B.

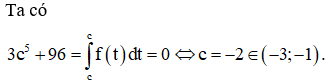
Câu 26:

Cho khối nón có bán kính đáy bằng r và độ dài đường sinh bằng 3 lần bán kính đáy. Thể tích của khối nón đã cho bằng

A. $\frac{\sqrt{2} {πr}^{3}}{3}$

B. $\frac{2 {πr}^{3}}{3}$

C. $\frac{2 \sqrt{2} {πr}^{3}}{3}$

D. $\frac{8 {πr}^{3}}{3}$

Xem đáp án

Chọn đáp án C.

Gọi h và l lần lượt là độ dài chiều cao và độ dài đường sinh của hình nón đã cho. Theo giả thiết thì l = 3r

Câu 27:

Tổng bình phương các nghiệm của phương trình ${(2^{x + 1})}^{x - 3}$ bằng

A. 20

B. 4

C. 2

D. 6

Xem đáp án

Chọn đáp án A.

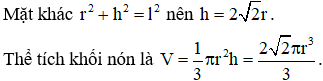
Câu 28:

Cho hàm số $y = f (x)$ có bảng biến thiên như sau:

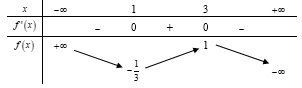
Số nghiệm thực của phương trình $4 f (2 - 3 x) + 1 = 0$ là

A. 1

B. 3

C. 2

D. 0

Xem đáp án

Chọn đáp án B.

Câu 29:

Cho khối lăng trụ đều $A B C . A' B' C'$ có tất cả các cạnh bằng 2a. Thể tích khối lăng trụ đã cho bằng

A. $2 \sqrt{3} a^{3}$

B. $\frac{\sqrt{3} a^{3}}{2}$

C. $\frac{2 \sqrt{3} a^{3}}{3}$

D. $\sqrt{3} a^{3}$

Xem đáp án

Chọn đáp án A.

Đây là tam giác đều cạnh 2a nên có diện tích

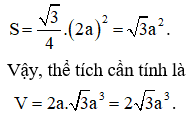
Câu 30:

Cho $F (x)$ là một nguyên hàm của hàm số $f (x) = \frac{6 x^{2} + 13 x + 11}{2 x^{2} + 5 x + 2}$ và thỏa mãn $P (2) = 7$ . Biết rằng $F (\frac{1}{2}) = \frac{5}{2} + a \ln 2 + b \ln 5$ , trong đó a, b là các số nguyên. Tính trung bình cộng của a và b.

A. 10

B. 8

C. 5

D. 3

Xem đáp án

Chọn đáp án D.

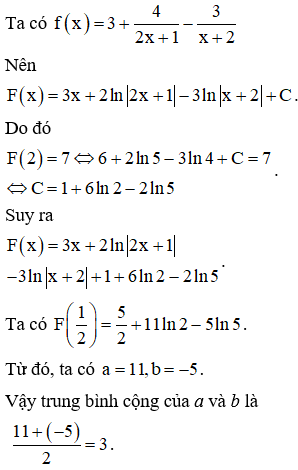
Câu 31:

Biết rằng tập hợp tất cả các giá trị của tham số m để hàm số $f (x) = \frac{x^{2} + 2 x + 2 m - 1}{x - m}$ đồng biến trên nửa khoảng $[2; + \infty)$ và $S = (- \infty; \frac{a}{b}]$ , trong đó a, b là các số nguyên dương và $\frac{a}{b}$ là phân số tối giản. Giá trị của $3 a - b$ bằng

A. 11

B. 23

C. 7

D. 19

Xem đáp án

Chọn đáp án C.

Câu 32:

Cho $\int_{3}^{5} \frac{d x}{x^{2} - x}$ với a, b, c là các số hữu tỷ. Giá trị của $b + 3 c^{2} - 2 a$ bằng

A. -2

B. 0

C. 3

D. 6

Xem đáp án

Chọn đáp án D.

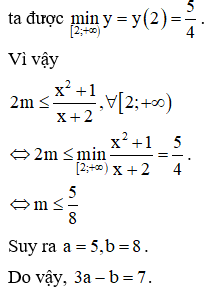
Câu 33:

Cho hình trụ $(T)$ có chiều cao bằng đường kính đáy, hai đáy là các hình tròn $(O; r)$ và $(O'; r)$ . Gọi A là điểm di động trên đường tròn $(O; r)$ v à B là điểm di động trên đường tròn $(O'; r)$ sao cho AB không là đường sinh của hình trụ $(T)$ . Khi thể tích khối tứ diện $O O' A B$ đạt giá trị lớn nhất thì đoạn thẳng AB có độ dài bằng

A. $\sqrt{3} r$

B. $(2 + \sqrt{2}) r$

C. $\sqrt{6} r$

D. $\sqrt{5} r$

Xem đáp án

Chọn đáp án C.

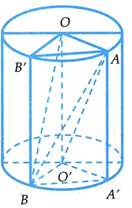
Kẻ các đường sinh AA', BB' của hình trụ (T).

Khi đó

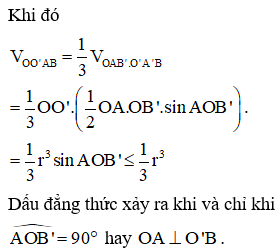
Như vậy, khối tứ diện có thể tích lớn nhất bằng

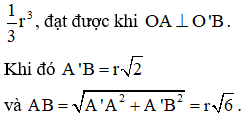
Câu 34:

Các loài cây xanh trong quá trình quang hợp sẽ nhận được một lượng nhỏ cacbon 14 (một đồng vị cacbon). Khi một bộ phận của cây đó bị chết thì hiện tượng quang hợp cũng sẽ ngưng và nó sẽ không nhận thêm cacbon 14 nữa. Lượng cacbon 14 của bộ phận đó sẽ phân hủy một cách chậm chạp, chuyển hóa thành nitơ 14. Gọi $P (t)$ là số phần trăm cacbon 14 còn lại trong một bộ phận của một cây sinh trưởng từ t năm trước đây thì được cho bởi công thức $P (t) = 100 . {(0, 5)}^{\frac{t}{5750}} (%)$ . Phân tích một mẫu gỗ từ một công trình kiến trúc cổ, người ta thấy lượng cacbon 14 còn lại trong gỗ là 45,78 (%). Hãy xác định niên đại của công trình kiến trúc đó.

A. 6482 năm.

B. 6481 năm.

C. 6428 năm.

D. 6248 năm.

Xem đáp án

Chọn đáp án A.

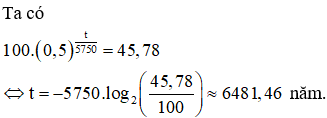
Do đó niên đại của công trình kiến trúc cổ là 6482 năm.

Câu 35:

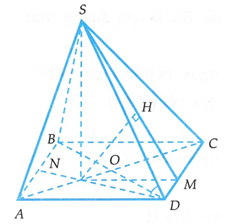
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu vuông góc của S lên mặt phẳng $(A B C D)$ trùng với trọng tâm G của tam giác ABD. Đường thẳng SD tạo với mặt phẳng một góc 60°. Khoảng cách giữa hai đường thẳng AB và SC bằng

A. $a \sqrt{\frac{15}{19}}$

B. $\frac{2 a \sqrt{285}}{57}$

C. $\frac{9 a \sqrt{285}}{19}$

D. $3 a \sqrt{\frac{5}{17}}$

Xem đáp án

Chọn đáp án A.

Gọi O là tâm của hình vuông và N là trung điểm của AB.

Khi đó G là giao điểm của AC và DN. Tam giác SGD vuông tại G nên $\hat{S D G}$ nhọn

Câu 36:

Cho x, y là các số thực thỏa mãn $\log_{9} x = \log_{12} y = \log_{16} (x + 2 y)$ . Giá trị của tỷ số $\frac{x}{y}$ là

A. $\frac{2 + \sqrt{2}}{2}$

B. $\sqrt{2} + 1$

C. $\frac{2 - \sqrt{2}}{2}$

D. $\sqrt{2} - 1$

Xem đáp án

Chọn đáp án D.

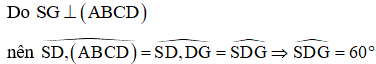
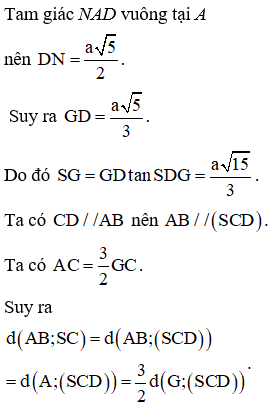
Câu 37:

Trong không gian Oxyz, cho ba điểm $A (0; 1; 2), B (2; - 2; 1), C (- 2; 0; 1)$ và mặt phẳng $(α)$ có phương trình $2 x + 2 y + z - 3 = 0$ . Biết rằng tồn tại duy nhất điểm $M (a; b; c)$ thuộc mặt phẳng $(α)$ sao cho $M A = M B = M C$ . Đẳng thức nào sau đây đúng?

A. $2 a + b - c = 0$

B. $2 a + 3 b - 4 c = 41$

C. $5 a + b + c = 0$

D. $a + 3 b + c = 0$

Xem đáp án

Chọn đáp án B.

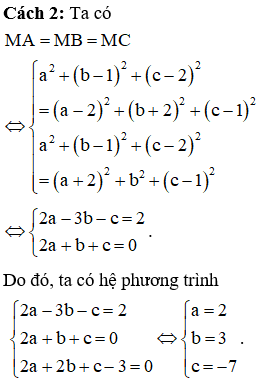
Câu 38:

Tập hợp điểm biểu diễn các số phức z thỏa mãn $2 |z - i| = |z - \bar{z} + 2 i|$ là

A. một đường thẳng.

B. một đường elip.

C. một parabol.

D. một đường tròn

Xem đáp án

Chọn đáp án C.

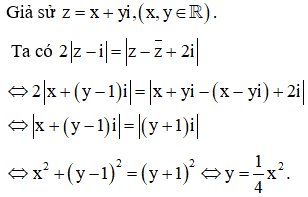
Vậy tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện đã cho là parabol (P) có phương trình $y = \frac{1}{4} x^{2}$

Câu 39:

Cho d là đường thẳng đi qua điểm $A (- 1; 3)$ và có hệ số góc m. Gọi S là tập hợp các giá trị của tham số m để đường thẳng d cắt đồ thị $(C)$ của hàm số $y = x^{3} - 3 x + 1$ tại ba điểm phân biệt A, B, C sao cho tiếp tuyến với đồ thị tại B và C cắt nhau tại điểm I nằm trên đường tròn đường kính BC. Tính tổng bình phương các phần tử thuộc tập hợp S.

A. $\frac{16}{9}$

B. $\frac{34}{9}$

C. $\frac{38}{9}$

D. $\frac{34}{3}$

Xem đáp án

Chọn đáp án B.

d và (C) cắt nhau tại ba điểm phân biệt

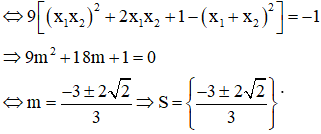
Tổng bình phương các phần tử của S là

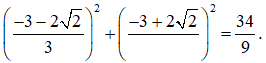
Câu 40:

Cho hàm số $g (x) = 2 x^{3} + x^{2} - 8 x + 7$ . Tồn tại bao nhiêu số nguyên dương m để phương trình $\sqrt{g (g (x) - 3) + m} = 2 g (x) - 5$ có 6 nghiệm thực phân biệt?

A. 25

B. 11

C. 13

D. 14

Xem đáp án

Chọn đáp án C.

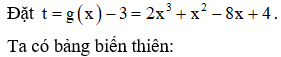
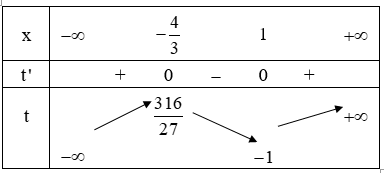
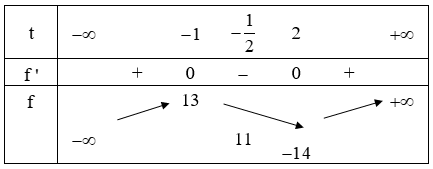
Do đó có 13 số nguyên dương m thỏa mãn yêu cầu bài toán.

Câu 41:

Trong không gian Oxyz, cho mặt cầu $(S) : {(x - 2)}^{2} + {(y - 5)}^{2} + {(z - 3)}^{2} = 27$ và đường thẳng $d : \frac{x - 1}{2} = \frac{y}{1} = \frac{z - 2}{2}$ . Mặt phẳng chứa đường thẳng d và cắt mặt cầu $(S)$ theo giao tuyến là đường tròn có bán kính nhỏ nhất. Nếu phương trình của $(P)$ là $a x + b y - z + c = 0$ thì

A. $a + b + c = 1$

B. $a + b + c = - 6$

C. $a + b + c = 6$

D. $a + b + c = 2$

Xem đáp án

Chọn đáp án C.

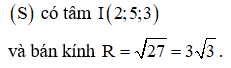
Gọi r là bán kính của đường tròn giao tuyến.

trong đó H là hình chiếu vuông góc của I trên d.

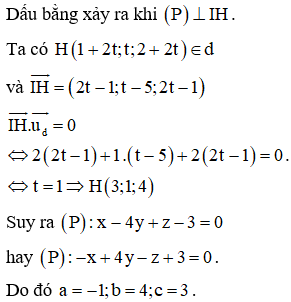
Câu 42:

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với $A B = 2, A D = 2 \sqrt{3}$ . Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng . Gọi M, N, P lần lượt là trung điểm của các cạnh SA, CD,CB. Tính côsin góc tạo bởi hai mặt phẳng $(M N P)$ và $(S C D)$ .

A. $\frac{2 \sqrt{435}}{145}$

B. $\frac{11 \sqrt{145}}{145}$

C. $\frac{2 \sqrt{870}}{145}$

D. $\frac{3 \sqrt{145}}{145}$

Xem đáp án

Chọn đáp án B.

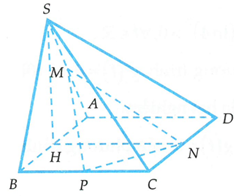
Chọn hệ trục tọa độ Oxyz sao cho H trùng với O, B thuộc tia Ox, N thuộc tia Oy và S thuộc tia Oz. Khi đó:

Câu 43:

Bệnh máu khó đông ở người do đột biến gen lặn nằm trên nhiễm sắc thể giới tính X, alen trội tương ứng quy định người bình thường. Một gia đình có người chồng bình thường còn người vợ mang gen dị hợp về tính trạng trên. Họ dự định sinh 2 người con, giả thiết rằng mỗi lần sinh chỉ sinh được một người con, xác suất để cả 2 người con không bị bệnh máu khó đông là bao nhiêu?

A. $\frac{9}{16}$

B. $\frac{15}{16}$

C. $\frac{1}{4}$

D. $\frac{3}{4}$

Xem đáp án

Chọn đáp án A.

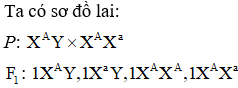
Cách 1: Từ kết quả lai, ta có xác suất sinh con như sau:

- Xác suất sinh 1 con gái bình thường và 1 con trai bình thường là

Để 2 người con đều bình thường thì chỉ xảy ra các trường hợp: hoặc 2 con gái bình thường hoặc 2 con trai bình thường hoặc 1 con gái bình thường và 1 con trai bình thường. Do đó xác suất để sinh được 2 người con bình thường là

Cách 2: Từ sơ đồ lai, ta có xác suất trong một lần sinh để sinh được người con bình thường là $\frac{3}{4}$

Do đó, xác suất để trong hai lần sinh đều sinh được người con bình thường là

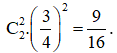
Câu 44:

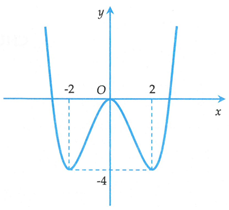
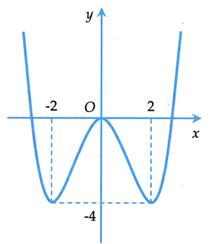
Cho hàm số $y = f (x)$ liên tục trên R và hàm số $y = f' (x)$ có đồ thị như hình bên. Bất phương trình $3^{f (x) + m} + 4^{f^{(x) + m}} \leq 5 f (x) + 2 + 5 m$ nghiệm đúng với mọi $x \in (- 1; 2)$ khi và chỉ khi

A. $- f (- 1) < m < 1 - f (2)$

B. $- f (2) < m < 1 - f (- 1)$

C. $- f (- 1) \leq m \leq 1 - f (2)$

D. $- f (2) \leq m \leq 1 - f (- 1)$

Xem đáp án

Chọn đáp án A.

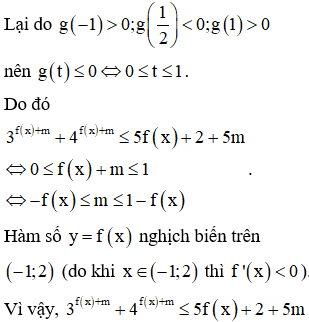
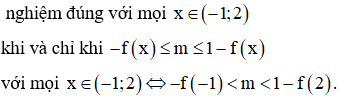
Câu 45:

Trong không gian Oxyz, cho điểm $M (2; - 3; 4)$ . Gọi $(P)$ là mặt phẳng đi qua M và cắt các trục $x' O x, y' O y, z' O z$ lần lượt tại các điểm D, E, F sao cho $O D = 2 O E = (m^{2} - 2 m + 2) O F \neq 0$ , trong đó m là tham số thực. Gọi S là tập hợp các giá trị của m để chỉ có đúng ba mặt phẳng thỏa mãn yêu cầu trên.

Tập hợp S có bao nhiêu tập hợp con khác rỗng?

A. 7

B. 3

C. 15

D. 4

Xem đáp án

Chọn đáp án A.

Suy ra số tập hợp con khác rỗng của S là $2^{3} - 1 = 7$

Câu 46:

Cho $f (x)$ là hàm đa thức thỏa mãn $f (x) - x f (1 - x) = x^{4} - 5 x^{3} + 12 x^{2} - 4 \forall x \in ℝ$ . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = f (x)$ trên tập $D = \{x \in ℝ | x^{4} - 10 x^{2} + 9 \leq 0\}$ . Giá trị của $21 m + 6 M + 2019$ bằng

A. 2235.

B. 2319.

C. 3045.

D. 3069.

Xem đáp án

Chọn đáp án A.

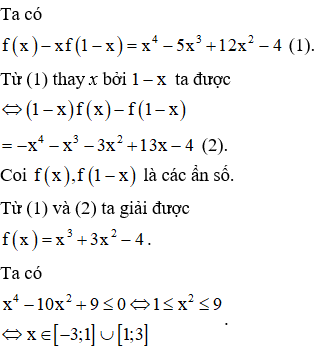
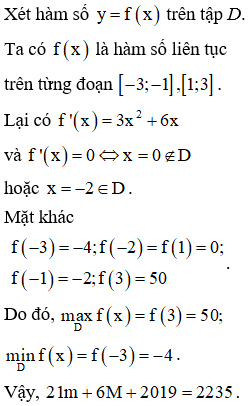
Câu 47:

Cho hình phẳng D giới hạn bởi các đường $y = \frac{(2 x^{2} + x) \sin x - (x - 1) \cos x}{x \sin x + \cos x}$ , trục hoành và hai đường thẳng $x = 0$ và $x = \frac{π}{4}$ . Biết rằng diện tích của hình phẳng D bằng $\frac{π^{2} + 4 π}{16} + a \ln 2 + b \ln (π + 4)$ , với a, b là các số hữu tỷ. Mệnh đề nào dưới đây đúng?

A. $2 a + b = 12$

B. $2 a - b = - 6$

C. $2 a - b = - 12$

D. $2 a + b = 6$

Xem đáp án

Chọn đáp án A.

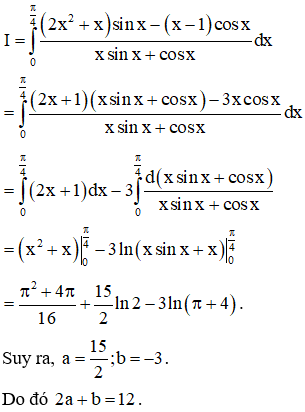
Câu 48:

Cho số phức z thỏa mãn $|z - 1 + 3 i| + |\bar{z} + 5 + i| = 2 \sqrt{65}$ . Giá trị nhỏ nhất của $|z + 2 + i|$ đạt được khi $z = a + b i$ với a, b là các số thực dương. Giá trị của $2 b + 3 a$ bằng

A. 19

B. 16

C. 24

D. 13

Xem đáp án

Chọn đáp án B.

Cách 1: (Sử dụng kiến thức Hình học)

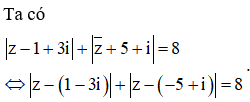
Gọi M, A, B, I lần lượt là điểm biểu diễn cho các số phức

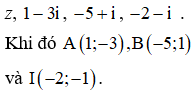
Có I là trung điểm của đoạn thẳng AB và

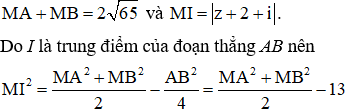
Áp dụng bất đẳng thức Cô-si, ta có

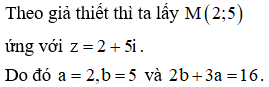
Cách 2: (Sử dụng kiến thức Đại số)

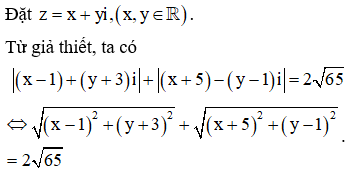
Áp dụng bất đẳng thức Bu-nhi-a-cốp-xky, ta có

Câu 49:

Trong hệ trục tọa độ Oxyz, cho tam giác ABC có $C (3; 2; 3)$ , đường cao AH nằm trên đường thẳng $d_{1} : \frac{x - 2}{1} = \frac{y - 3}{1} = \frac{z - 3}{- 2}$ và đường phân giác trong BD của góc B nằm trên đường thẳng $d_{2}$ có phương trình $\frac{x - 1}{1} = \frac{y - 4}{- 2} = \frac{z - 3}{1}$ . Diện tích tam giác ABC bằng

A. 4

B. $2 \sqrt{3}$

C. $4 \sqrt{3}$

D. 8

Xem đáp án

Chọn đáp án B.

nên trường hợp này bị loại.

Câu 50:

Cho hàm số $y = f (x)$ có đạo hàm trên R và đồ thị $(C)$ . Tiếp tuyến của đồ thị $(C)$ tại điểm $(2; m)$ có phương trình là $y = 4 x - 6$ . Tiếp tuyến của các đồ thị hàm số $y = f [f (x)]$ và $y = f (3 x^{2} - 10)$ tại điểm có hoành độ bằng 2 có phương trình lần lượt là $y = a x + b$ và $y = c x + d$ . Tính giá trị của biểu thức $S = 4 a + 3 c - 2 b + d$ .

A. S = -26

B. S = 176

C. S = 178

D. S = 174

Xem đáp án

Chọn đáp án D.