ĐGNL ĐHQG Hà Nội - Tư duy định lượng - Bất phương trình
-
488 lượt thi
-
42 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Tập nghiệm SS của bất phương trình \[5x - 1 \ge \frac{{2x}}{5} + 3\]là:
 Xem đáp án
Xem đáp án
Bất phương trình\[5x - 1 \ge \frac{{2x}}{5} + 3\]
\[ \Leftrightarrow 25x - 5 \ge 2x + 15 \Leftrightarrow 23x \ge 20 \Leftrightarrow x \ge \frac{{20}}{{23}}.\]
Đáp án cần chọn là: D
Câu 2:
Tổng các nghiệm nguyên của bất phương trình \(\frac{{x - 2}}{{\sqrt {x - 4} }} \le \frac{4}{{\sqrt {x - 4} }}\) bằng:
 Xem đáp án
Xem đáp án
Điều kiện: x >4.
Bất phương trình tương đương :
\[x - 2 \le 4 \Leftrightarrow x \le 6 \Rightarrow 4 < x \le 6\]
Mà \[x \in \mathbb{Z} \Rightarrow x = 5;x = 6 \Rightarrow S = 5 + 6 = 11\]
Đáp án cần chọn là: B
</>
Câu 3:
Tổng các nghiệm nguyên của bất phương trình \[x\left( {2 - x} \right) \ge x\left( {7 - x} \right) - 6\left( {x - 1} \right)\] trên đoạn \[\left[ { - 10;10} \right]\;\]bằng:
 Xem đáp án
Xem đáp án
Bất phương trình \[x\left( {2 - x} \right) \ge x\left( {7 - x} \right) - 6\left( {x - 1} \right)\]
\[ \Leftrightarrow 2x - {x^2} \ge 7x - {x^2} - 6x + 6 \Leftrightarrow x \ge 6\]Mà\[x \in \mathbb{Z};x \in \left[ { - 10;10} \right] \Rightarrow x \in \left\{ {6;7;8;9;10} \right\}\]
Vậy tổng các nghiệm nguyên cần tìm là: 6+7+8+9+10=40.
Đáp án cần chọn là: D
Câu 4:
Tập nghiệm của bất phương trình: \[ - {x^2} + 6x + 7\; \ge 0\;\] là:
 Xem đáp án
Xem đáp án
Ta có \[ - {x^2} + 6x + 7 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 7}\\{x = - 1}\end{array}} \right.\]
Bảng xét dấu
![Tập nghiệm của bất phương trình: \[ - {x^2} + 6x + 7\; \ge 0\;\] là:Ta có \[ - {x^2} + 6x + 7 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 7}\\{x = - 1}\end{array}} \right.\]Bảng (ảnh 1)](https://video.vietjack.com/upload2/images/1652772499/1652772699-image1.png)
Dựa vào bảng xét dấu \[ - {x^2} + 6x + 7\; \ge 0 \Leftrightarrow - 1 \le x \le 7.\]
Đáp án cần chọn là: B
Câu 5:
Giải bất phương trình \[ - 2{x^2} + 3x - 7 \ge 0.\].
 Xem đáp án
Xem đáp án
Ta có\[ - 2{x^2} + 3x - 7\; = 0\] vô nghiệm.
Bảng xét dấu
![Giải bất phương trình \[ - 2{x^2} + 3x - 7 \ge 0.\]. Ta có\[ - 2{x^2} + 3x - 7\; = 0\] vô nghiệm.Bảng xét dấuDựa vào bảng xét dấu\[ - 2{x^2} + 3x - 7 \ge 0\, \Leftrightarrow \,x \in \emptyse (ảnh 1)](https://video.vietjack.com/upload2/images/1652772499/1652772699-image2.png)
Dựa vào bảng xét dấu\[ - 2{x^2} + 3x - 7 \ge 0\, \Leftrightarrow \,x \in \emptyset \]
Đáp án cần chọn là: C
Câu 6:
Cho bất phương trình \[{x^2} - 8x + 7 \ge 0\]. Trong các tập hợp sau đây, tập nào có chứa phần tử không phải là nghiệm của bất phương trình.
 Xem đáp án
Xem đáp án
Ta có \[f(x) = {x^2} - 8x + 7 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x = 7}\end{array}} \right.\]Bảng xét dấu
![Cho bất phương trình \[{x^2} - 8x + 7 \ge 0\]. Trong các tập hợp sau đây, tập nào có chứa phần tử không phải là nghiệm của bất phương trình.Ta có \[f(x) = {x^2} - 8x + 7 = 0 \Leftrightarrow \ (ảnh 1)](https://video.vietjack.com/upload2/images/1652772499/1652772699-image3.png)
Dựa vào bảng xét dấu\[f(x) \ge 0 \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x \le 1}\\{x \ge 7}\end{array}} \right.\]
Tập nghiệm của bất phương trình là \[S = \left( { - \infty ;1} \right] \cup \,\left[ {7; + \infty } \right)\]
Vì\[\frac{{13}}{2} \in \left[ {6; + \infty } \right)\]và \[\frac{{13}}{2} \notin S\]nên\[\left[ {6; + \infty } \right)\]thỏa yêu cầu bài toán.
Đáp án cần chọn là: D
Câu 7:
Giải bất phương trình \[x\left( {x + 5} \right) \le 2\left( {{x^2} + 2} \right)\] ta được nghiệm:
 Xem đáp án
Xem đáp án
Bất phương trình
\[x\left( {x + 5} \right) \le 2\left( {{x^2} + 2} \right) \Leftrightarrow {x^2} + 5x \le 2{x^2} + 4 \Leftrightarrow {x^2} - 5x + 4 \ge 0\]
Xét phương trình \[{x^2} - 5x + 4 = 0 \Leftrightarrow (x - 1)(x - 4) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x = 4}\end{array}} \right.\]
Lập bảng xét dấu:
![Giải bất phương trình \[x\left( {x + 5} \right) \le 2\left( {{x^2} + 2} \right)\] ta được nghiệm:Bất phương trình\[x\left( {x + 5} \right) \le 2\left( {{x^2} + 2} \right) \Leftrightarrow {x^ (ảnh 1)](https://video.vietjack.com/upload2/images/1652772499/1652772699-image4.png)
Dựa vào bảng xét dấu, ta thấy nghiệm của bất phương trình\[{x^2} - 5x + 4 \ge 0\] là\[x \in \left( { - \,\infty ;1} \right] \cup \left[ {4; + \,\infty } \right).\]
Đáp án cần chọn là: C
Câu 8:
Cặp bất phương trình nào sau đây là tương đương?
 Xem đáp án
Xem đáp án
Đặt \[f\left( x \right) = {x^2}\left( {x - 2} \right).\]
Phương trình \[{x^2} = 0 \Leftrightarrow x = 0\] và\[x - 2 = 0 \Leftrightarrow x = 2.\]
Lập bảng xét dấu
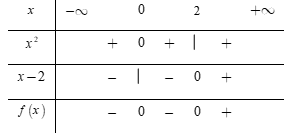
Dựa vào bảng xét dấu ta thấy:
+) Đáp án A: \[x - 2 \le 0 \Leftrightarrow x \le 2\] và\[{x^2}\left( {x - 2} \right) \le 0 \Leftrightarrow x \le 2\] nên hai bất phương trình tương đương. Chọn A.
+) Đáp án B: \[x - 2 < 0 \Leftrightarrow x < 2\] và \[{x^2}\left( {x - 2} \right) >0 \Leftrightarrow x >2\] nên hai bất phương trình không tương đương. Loại B.
+) Đáp án C: \[x - 2 < 0 \Leftrightarrow x < 2\] và\[{x^2}(x - 2) < 0 \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x < 2}\\{x \ne 0}\end{array}} \right.\] nên hai bất phương trình không tương đương. Loại C.
+) Đáp án D:\[{x^2}(x - 2) \ge 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x \ge 2}\end{array}} \right.\] và \[x - 2 \ge 0 \Leftrightarrow x \ge 2\] nên hai bất phương trình không tương đương. Loại D.
Đáp án cần chọn là: A
Câu 9:
Xác định m để với mọi x ta có \[ - 1 \le \frac{{{x^2} + 5x + m}}{{2{x^2} - 3x + 2}} < 7\]
 Xem đáp án
Xem đáp án
- Vì \[2{x^2} - 3x + 2 >0\,\,\forall x \in \mathbb{R}\]
- Bất phương trình nên: \[ - 1 \le \frac{{{x^2} + 5x + m}}{{2{x^2} - 3x + 2}} < 7\] có tập nghiệm là \[\mathbb{R}\] khi hệ sau có tập nghiệm là \[\mathbb{R}\]:
\(\left\{ {\begin{array}{*{20}{c}}{ - 1(2{x^2} - 3x + 2) \le {x^2} + 5x + m}\\{{x^2} + 5x + m < 7(2{x^2} - 3x + 2)}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{13{x^2} - 26x + 14 - m >0(1)}\\{3{x^2} + 2x + m + 2 \ge 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2)}\end{array}} \right.} \right.\)- Ta có (1) có tập nghiệm là \[\mathbb{R}\] khi\[{\rm{\Delta ' < }}0 \Leftrightarrow - 13 + 13m < 0 \Leftrightarrow m < 1\,\,\,\,\,\,\,\,\,\left( 3 \right)\]
- (2) có tập nghiệm là \[\mathbb{R}\] khi\[{\rm{\Delta '}} \le 0 \Leftrightarrow - 5 - 3m \le 0 \Leftrightarrow m \ge - \frac{5}{3}\,\,\,\,\,\,\,\,\,\left( 4 \right)\]
Từ (2) và (4), ta có\[ - \frac{5}{3} \le m < 1\]
Đáp án cần chọn là: A
Câu 10:
Bất phương trình có nghiệm là
 Xem đáp án
Xem đáp án
Trả lời:
Trường hợp 1:
Trường hợp 2:
Đáp án cần chọn là: A
Câu 11:
Bất phương trình \[\sqrt { - {x^2} + 6x - 5} >8 - 2x\]có nghiệm là:
 Xem đáp án
Xem đáp án
Ta có\[\sqrt { - {x^2} + 6x - 5} >8 - 2x\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{ - {x^2} + 6x - 5 \ge 0}\\{8 - 2x < 0}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{8 - 2x \ge 0}\\{ - {x^2} + 6x - 5 >{{(8 - 2x)}^2}}\end{array}} \right.}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{1 \le x \le 5}\\{x >4}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{x \le 4}\\{ - 5{x^2} + 38x - 69 >0}\end{array}} \right.}\end{array}} \right.\)</>
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{1 \le x \le 5}\\{x >4}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{x \le 4}\\{3 < x < \frac{{23}}{5}}\end{array}} \right.}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{4 < x \le 5}\\{3 < x \le 4}\end{array}} \right. \Leftrightarrow 3 < x \le 5\)
Câu 12:
Tập nghiệm SS của bất phương trình \[\frac{{ - \,2{x^2} + 7x + 7}}{{{x^2} - 3x - 10}} \le - 1\]là
 Xem đáp án
Xem đáp án
Điều kiện: \[{x^2} - 3x - 10 \ne 0 \Leftrightarrow (x + 2)(x - 5) \ne 0 \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x \ne - 2}\\{x \ne 5}\end{array}} \right.\]
Bất phương trình\[\frac{{ - \,2{x^2} + 7x + 7}}{{{x^2} - 3x - 10}} \le - 1 \Leftrightarrow \frac{{ - 2{x^2} + 7x + 7}}{{{x^2} - 3x - 10}} + 1 \le 0 \Leftrightarrow \frac{{ - {x^2} + 4x - 3}}{{{x^2} - 3x - 10}} \le 0\,\,\,\,\left( * \right)\]
Bảng xét dấu
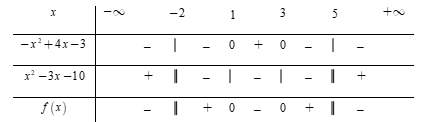
Dựa vào bảng xét dấu, bất phương trình \[\left( * \right) \Leftrightarrow x \in \left( { - \,\infty ; - \,2} \right) \cup \left[ {1;3} \right] \cup \left( {5; + \,\infty } \right).\]Đáp án cần chọn là: C
Câu 13:
Nghiệm của hệ bất phương trình: \(\left\{ {\begin{array}{*{20}{c}}{2{x^2} - x - 6 \le 0}\\{{x^3} + {x^2} - x - 1 \ge 0}\end{array}} \right.\) là:
 Xem đáp án
Xem đáp án
Ta có\[2{x^2} - x - 6 \le 0 \Leftrightarrow - \frac{3}{2} \le x \le 2,\left( I \right)\]
\[{x^3} + {x^2} - x - 1 \ge 0 \Leftrightarrow \left( {x + 1} \right)\left( {{x^2} - 1} \right) \ge 0 \Leftrightarrow \left( {x - 1} \right){\left( {x + 1} \right)^2} \ge 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{ - 1}\\{x \ge 1}\end{array}} \right.\,\,\,\,\left( {II} \right)\]
Từ (I) và (II) suy ra nghiệm của hệ là\[S = \left[ {1;2} \right] \cup \left\{ { - 1} \right\}\]
Câu 14:
Bất phương trình: \[\left| {{x^4} - 2{x^2} - 3} \right| \le {x^2} - 5\] có bao nhiêu nghiệm nghiệm nguyên?
 Xem đáp án
Xem đáp án
Đặt \[t = {x^2} \ge 0\]
Ta có \[\left| {{t^2} - 2t - 3} \right| \le t - 5\]
Nếu \[{t^2} - 2t - 3 \ge 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t \le - 1}\\{t \ge 3}\end{array}} \right.\] thì ta có\[{t^2} - 3t + 2 \le 0 \Leftrightarrow 1 \le t \le 2\] loại
Nếu\[{t^2} - 2t - 3 < 0 \Leftrightarrow - 1 < t < 3\] thì ta có\[ - {t^2} + t + 8 \le 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t \le \frac{{1 - \sqrt {33} }}{2}}\\{t \ge \frac{{1 + \sqrt {33} }}{2}}\end{array}} \right.\] loại.
Đáp án cần chọn là: A
</>
Câu 15:
Cho bất phương trình: \[{x^2} - 2x \le \left| {x - 2} \right| + ax - 6\]. Giá trị dương nhỏ nhất của a để bất phương trình có nghiệm gần nhất với số nào sau đây:
 Xem đáp án
Xem đáp án
Trường hợp 1:\[x \in \left[ {2; + \infty } \right)\]
Khi đó bất phương trình đã cho trở thành:
\[{x^2} - \left( {a + 3} \right)x + 8 \le 0 \Leftrightarrow a \ge x + \frac{8}{x} - 3 \ge 4\sqrt 2 - 3 \approx 2,65\forall x \in \left[ {2; + \infty } \right)\]
Dấu xảy ra khi\[x = 2\sqrt 2 \]
Trường hợp 2:\[x \in \left( { - \infty ;2} \right)\]
Khi đó bất phương trình đã cho trở thành:
\[{x^2} - \left( {a + 1} \right)x + 4 \le 0\]
\[ \Leftrightarrow ax \ge {x^2} - x + 4\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{a \ge \frac{{{x^2} - x + 4}}{x}\,\,khi\,\,x \in (0;2)}\\{a \le \frac{{{x^2} - x + 4}}{x}\,\,\,\,khi\,x \in ( - \infty ;0)}\end{array}} \right.\,\,\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{a \ge x + \frac{4}{x} - 1\,\,\,khi\,\,\,x \in (0;2)\,\,\,\,\,(1)}\\{a \le x + \frac{4}{x} - 1\,\,\,khi\,\,\,x \in ( - \infty ;0)\,\,\,\,\,(2)}\end{array}} \right.\)
Giải (1) ta được a >3 (theo bất đẳng thức Cauchy).
Giải (2): \[a \le x + \frac{4}{x} - 1 \Leftrightarrow a \le - 2\sqrt {x.\frac{4}{x}} - 1 = - 5\]
Vậy giá trị dương nhỏ nhất của a gần với số 2,6.
Đáp án cần chọn là: D
Câu 16:
Số nghiệm của phương trình: \[\sqrt {x + 8 - 2\sqrt {x + 7} } = 2 - \sqrt {x + 1 - \sqrt {x + 7} } \] là:
 Xem đáp án
Xem đáp án
Điều kiện\[x \ge - 7\]
Đặt \[t = \sqrt {x + 7} \] điều kiện \[t \ge 0\]
Ta có\[\sqrt {{t^2} + 1 - 2t} = 2 - \sqrt {{t^2} - 6 - t} \Leftrightarrow \left| {t - 1} \right| = 2 - \sqrt {{t^2} - t - 6} \]
Nếu \[t \ge 1\] thì ta có\[3 - t = \sqrt {{t^2} - t - 6} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{t^2} - t - 6 = 9 - 6t + {t^2}}\\{t \le 3}\end{array}} \right. \Leftrightarrow t = 3 \Leftrightarrow \sqrt {x + 7} = 3 \Leftrightarrow x = 2\]
Nếu t < 1 thì ta có \[1 + t = \sqrt {{t^2} - t - 6} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{t^2} - t - 6 = 1 + 2t + {t^2}}\\{t \ge - 1}\end{array}} \right. \Leftrightarrow t = - \frac{7}{3}\;\;\left( l \right)\]
Đáp án cần chọn là: B
</>
Câu 17:
Hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{{x^2} - 1 \le 0}\\{x - m >0}\end{array}} \right.\)có nghiệm khi
 Xem đáp án
Xem đáp án
Ta có: \(\left\{ {\begin{array}{*{20}{c}}{{x^2} - 1 \le 0}\\{x - m >0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - 1 \le x \le 1}\\{x >m}\end{array}} \right.\)
Do đó hệ có nghiệm khi m < 1.
Đáp án cần chọn là: C
</>
Câu 18:
Xác định m để phương trình \[\left( {x - 1} \right)\left[ {{x^2} + 2\left( {m + 3} \right)x + 4m + 12} \right] = 0\] có ba nghiệm phân biệt lớn hơn –1.
 Xem đáp án
Xem đáp án
Ta có \[\left( {x - 1} \right)\left[ {{x^2} + 2\left( {m + 3} \right)x + 4m + 12} \right] = 0\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{{x^2} + 2(m + 3)x + 4m + 12 = 0( * )}\end{array}} \right.\)
Giả sử phương trình (∗) có hai nghiệm phân biệt \[{x_1},{x_2}\], theo Vi-et ta có\(\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = - 2(m + 3)}\\{{x_1}.{x_2} = 4m + 12}\end{array}} \right.\)
Để phương trình \[\left( {x - 1} \right)\left[ {{x^2} + 2\left( {m + 3} \right)x + 4m + 12} \right] = 0\] có ba nghiệm phân biệt lớn hơn −1. thì phương trình (∗) có hai nghiệm phân biệt \[{x_1},{x_2}\] khác 1 và đều lớn hơn −1.
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\Delta \prime >0}\\{1 + 2(m + 3) + 4m + 12 \ne 0}\\{{x_2} >{x_1} >- 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{{(m + 3)}^2} - (4m + 12) >0}\\{6m + 19 \ne 0}\\{({x_1} + 1) + ({x_2} + 1) >0}\\{({x_1} + 1)({x_2} + 1) >0}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{m^2} + 2m - 3 >0}\\{m \ne - \frac{{19}}{6}}\\{ - 2(m + 3) + 2 >0}\\{4m + 12 - 2(m + 3) + 1 >0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\left[ {\begin{array}{*{20}{c}}{m >1}\\{m < - 3}\end{array}} \right.}\\{m \ne - \frac{{19}}{6}}\\{m < - 2}\\{m >- \frac{7}{2}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - \frac{7}{2} < m < - 3}\\{m \ne - \frac{{19}}{6}}\end{array}} \right.\)
Đáp án cần chọn là: D
Câu 19:
Để phương trình sau có 4 nghiệm phân biệt: \[\left| {10x - 2{x^2} - 8} \right| = {x^2} - 5x + a\] thì giá trị của tham số a là:
 Xem đáp án
Xem đáp án
Xét phương trình: \[\left| {10x - 2{x^2} - 8} \right| = {x^2} - 5x + a\](1)
\[ \Leftrightarrow a = \left| {10x - 2{x^2} - 8} \right| - {x^2} + 5x\]
Xét \[f\left( x \right) = \left| {10x - 2{x^2} - 8} \right| - {x^2} + 5x\]
\( = \left\{ {\begin{array}{*{20}{c}}{(10x - 2{x^2} - 8) - {x^2} + 5x\,\,\,khi\,\,10x - 2{x^2} - 8 \ge 0}\\{ - (10x - 2{x^2} - 8) - {x^2} + 5x\,\,\,\,khi\,\,\,10x - 2{x^2} - 8 < 0}\end{array}} \right.\,\,\,\,\)
\( = \left\{ {\begin{array}{*{20}{c}}{ - 3{x^2} + 15x - 8\,\,\,khi\,\,\,1 \le x \le 4}\\{{x^2} - 5x + 8\,\,\,\,khi\,\,x \le 1 \vee x \ge 4}\end{array}} \right.\)
Bảng biến thiên:
![Để phương trình sau có 4 nghiệm phân biệt: \[\left| {10x - 2{x^2} - 8} \right| = {x^2} - 5x + a\] thì giá trị của tham số a là:Xét phương trình: \[\left| {10x - 2{x^2} - 8} \right| = {x^2} - (ảnh 1)](https://video.vietjack.com/upload2/images/1652772499/1652772699-image7.png)
Dựa vào bảng biến thiên ta có phương trình (1) có 4 nghiệm phân biệt\[ \Leftrightarrow 4 < a < \frac{{43}}{4}\]
Đáp án cần chọn là: D
Câu 20:
Để bất phương trình \[\sqrt {(x + 5)(3 - x)} \le {x^2} + 2x + a\] nghiệm đúng \[\forall x \in [ - 5;3]\]tham số a phải thỏa điều kiện:
\[\sqrt {\left( {x + 5} \right)\left( {3 - x} \right)} \le {x^2} + 2x + a \Leftrightarrow \sqrt { - {x^2} - 2x + 15} - {x^2} - 2x \le a\]
 Xem đáp án
Xem đáp án
Đặt\[t = \sqrt { - {x^2} - 2x + 15} \]ta có bảng biến thiên
![Để bất phương trình \[\sqrt {(x + 5)(3 - x)} \le {x^2} + 2x + a\] nghiệm đúng \[\forall x \in [ - 5;3]\]tham số a phải thỏa điều kiện:\[\sqrt {\left( {x + 5} \right)\left( {3 - x} \right)} (ảnh 1)](https://video.vietjack.com/upload2/images/1652772499/1652772699-image8.png)
Suy ra\[t \in \left[ {0;4} \right]\]
Bất phương trình đã cho thành\[{t^2} + t - 15 \le a\]
Xét hàm\[f\left( t \right) = {t^2} + t - 15\]với \[t \in \left[ {0;4} \right]\]
Ta có bảng biến thiên
![Để bất phương trình \[\sqrt {(x + 5)(3 - x)} \le {x^2} + 2x + a\] nghiệm đúng \[\forall x \in [ - 5;3]\]tham số a phải thỏa điều kiện:\[\sqrt {\left( {x + 5} \right)\left( {3 - x} \right)} (ảnh 2)](https://video.vietjack.com/upload2/images/1652772499/1652772699-image9.png)
Bất phương trình\[{t^2} + t - 15 \le a\]nghiệm đúng\[\forall t \in \left[ {0;4} \right]\]khi và chỉ khi\[a \ge 5.\]
Đáp án cần chọn là: C
Câu 21:
Để phương trình: \[\left| {x + 3} \right|(x - 2) + m - 1 = 0\] có đúng một nghiệm, các giá trị của tham số m là:
 Xem đáp án
Xem đáp án
Ta có\[\left| {x + 3} \right|\left( {x - 2} \right) + m - 1 = 0 \Leftrightarrow m = 1 - \left| {x + 3} \right|\left( {x - 2} \right)\]
Xét hàm số\[y = 1 - \left| {x + 3} \right|(x - 2)\]
Ta có\(y = \left\{ {\begin{array}{*{20}{c}}{ - {x^2} - x + 7\,\,\,khi\,\,\,x \ge - 3}\\{{x^2} + x - 5\,\,\,\,khi\,\,\,\,x < - 3}\end{array}} \right.\)
Bảng biến thiên của \[y = 1 - \left| {x + 3} \right|(x - 2)\]
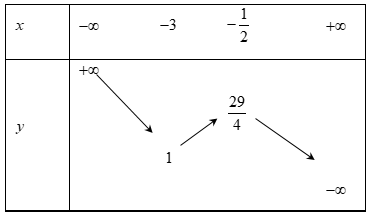
Dựa vào bảng trên phương trình có đúng 1 nghiệm khi và chỉ khi\(\left[ {\begin{array}{*{20}{c}}{m < 1}\\{m >\frac{{29}}{4}}\end{array}} \right.\)
Đáp án cần chọn là: A
Câu 22:
Bất phương trình \[\left( {x + 1} \right)\left( {x + 4} \right) < 5\sqrt {{x^2} + 5x + 28} \] có nghiệm là
 Xem đáp án
Xem đáp án
TXĐ: \[D = \mathbb{R}\]\[\left( {x + 1} \right)\left( {x + 4} \right) < 5\sqrt {{x^2} + 5x + 28} \Leftrightarrow {x^2} + 5x + 4 - 5\sqrt {{x^2} + 5x + 28} < 0\](1)
Đặt \[\sqrt {{x^2} + 5x + 28} = t\left( {t >0} \right)\]
(1) trở thành:\[{t^2} - 5t - 24 < 0 \Leftrightarrow - 3 < t < 8\]
\[ \Rightarrow {x^2} + 5x + 28 < 64 \Leftrightarrow {x^2} + 5x - 36 < 0 \Leftrightarrow - 9 < x < 4\]
Đáp án cần chọn là: B
Câu 23:
Tập nghiệm của bất phương trình \[\left| {x - 3} \right| >- 1\]là
 Xem đáp án
Xem đáp án
Vì\[\left| {x - 3} \right| \ge 0,\,\,\forall x \in \mathbb{R}\] nên suy ra\[\left| {x - 3} \right| >- 1,\,\,\forall x \in \mathbb{R}.\]
Vậy tập nghiệm của bất phương trình là \[S = \mathbb{R}.\]
Đáp án cần chọn là: D
Câu 24:
Tìm m để bất phương trình có nghiệm .
 Xem đáp án
Xem đáp án
Ta có:\[( * ) \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{3 - \frac{{x + 1}}{{{x^3} - {x^2} - 3x + 3}} < 0}\\{x >{m^2} + m}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\frac{{\left( {x - 2} \right)\left( {3{x^2} + 3x - 4} \right)}}{{\left( {x - 1} \right)\left( {{x^2} - 3} \right)}} < 0}\\{x >{m^2} + m}\end{array}} \right.\left( {**} \right)\]
Bảng xét dấu:
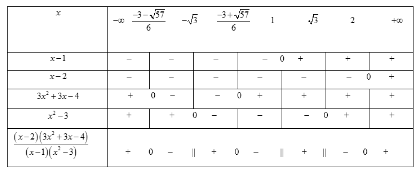
Tập nghiệm của bất phương trình \[\frac{{\left( {x - 2} \right)\left( {3{x^2} + 3x - 4} \right)}}{{\left( {x - 1} \right)\left( {{x^2} - 3} \right)}} < 0\] là\[S = \left( {\frac{{ - 3 - \sqrt {57} }}{6}; - \sqrt 3 } \right) \cup \left( {\frac{{ - 3 + \sqrt {57} }}{6};1} \right) \cup \left( {\sqrt 3 ;2} \right)\]
Do đó bất phương trình (∗) có nghiệm khi và chỉ khi hệ bất phương trình(∗∗) có nghiệm \[ \Leftrightarrow {m^2} + m < 2 \Leftrightarrow {m^2} + m - 2 < 0 \Leftrightarrow - 2 < m < 1\]
Vậy\[ - 2 < m < 1\] là giá trị cần tìm.
Đáp án cần chọn là: C
Câu 25:
Một viên gạch hình vuông có cạnh thay đổi được đặt nội tiếp trong một hình vuông có cạnh bằng 20cm, tạo thành bốn tam giác xung quanh như hình vẽ.
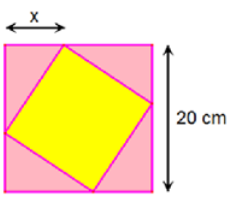
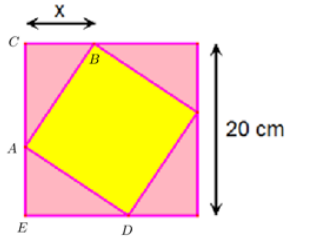
Tìm tập hợp các giá trị của x để diện tích viên gạch không vượt quá 208cm2.
 Xem đáp án
Xem đáp án
Ta có:\[\angle CAB + \angle BAD + \angle DAE = {180^o}\]
\[ \Rightarrow \angle CAB + \angle EAD = {90^o}\]
Mà \[\angle CAB + \angle CBA = {90^o}\] (\[\Delta CAB\]vuông tại C)
\[ \Rightarrow \angle CBA = \angle EAD\] kết hợp\[AB = AD\,\,\,\left( {gt} \right)\]
\[\begin{array}{*{20}{l}}{ \Rightarrow {\rm{\Delta }}CAB = {\rm{\Delta }}EDA\,\,\,\left( {ch - gn} \right)}\\{ \Rightarrow CB = EA = x \Rightarrow CA = CE - EA = 20 - x\,\,\,\,\left( {cm} \right)}\end{array}\]
Diện tích viên gạch là\[S = A{B^2} = C{B^2} + C{A^2} = {x^2} + {\left( {20 - x} \right)^2}\]
Vì \[S \le 208 \Leftrightarrow {x^2} + {\left( {20 - x} \right)^2} \le 208 \Leftrightarrow 2{x^2} - 40x + 192 \le 0 \Leftrightarrow 8 \le x \le 12\]
Đáp án cần chọn là: A
Câu 26:
Tập nghiệm của bất phương trình \[\left( {\sqrt {2x + 4} - \sqrt {x + 1} } \right)\left( {\sqrt {2x + 1} + \sqrt {x + 4} } \right) \le x + 3\] là tập con của tập hợp nào sau đây?
 Xem đáp án
Xem đáp án
ĐKXĐ:\[x \ge - \frac{1}{2}\]
\[(\sqrt {2x + 4} - \sqrt {x + 1} )(\sqrt {2x + 1} + \sqrt {x + 4} ) \le x + 3\]
\[ \Leftrightarrow (\sqrt {2x + 4} - \sqrt {x + 1} )(\sqrt {2x + 4} + \sqrt {x + 1} )(\sqrt {2x + 1} + \sqrt {x + 4} ) \le (x + 3)(\sqrt {2x + 4} + \sqrt {x + 1} )\]\[ \Leftrightarrow (x + 3)(\sqrt {2x + 1} + \sqrt {x + 4} ) \le (x + 3)(\sqrt {2x + 4} + \sqrt {x + 1} )\]
\[ \Leftrightarrow (x + 3)(\sqrt {2x + 1} + \sqrt {x + 4} - \sqrt {2x + 4} - \sqrt {x + 1} ) \le 0\]
\[ \Leftrightarrow \sqrt {2x + 1} + \sqrt {x + 4} - \sqrt {2x + 4} - \sqrt {x + 1} \le 0\] (do x + 3 >0\[\forall x \ge - \frac{1}{2}\])
\[ \Leftrightarrow \sqrt {2x + 1} + \sqrt {x + 4} \le \sqrt {2x + 4} + \sqrt {x + 1} \]
\[ \Leftrightarrow 3x + 5 + 2\sqrt {(2x + 1)(x + 4)} \le 3x + 5 + 2\sqrt {(2x + 4)(x + 1)} \]
\[ \Leftrightarrow (2x + 1)(x + 4) \le (2x + 4)(x + 1)\]
\[ \Leftrightarrow 2{x^2} + 9x + 4 \le 2{x^2} + 6x + 4\]
\[ \Leftrightarrow 3x \le 0 \Leftrightarrow x \le 0\]
Kết hợp ĐKXĐ\[ \Rightarrow x \in \left[ { - \frac{1}{2};0} \right] \subset \left( { - \frac{2}{3};\frac{1}{2}} \right)\]Đáp án cần chọn là: A
Câu 27:
Cho biểu thức \[f\left( x \right) = \left( {x + 5} \right)\left( {3 - x} \right).\]Tập hợp tất cả các giá trị của x thỏa mãn bất phương trình f(x) ≤ 0 là
 Xem đáp án
Xem đáp án
Ta có\[f\left( x \right) = 0 \Leftrightarrow \left( {x + 5} \right)\left( {3 - x} \right) = 0.\]
Phương trình \[x + 5 = 0 \Leftrightarrow x = - \,5\] và \[3 - x = 0 \Leftrightarrow x = 3.\]
Bảng xét dấu:
![Cho biểu thức \[f\left( x \right) = \left( {x + 5} \right)\left( {3 - x} \right).\]Tập hợp tất cả các giá trị của x thỏa mãn bất phương trình f(x) ≤ 0 làTa có\[f\left( x \right) = 0 \Leftri (ảnh 1)](https://video.vietjack.com/upload2/images/1652772499/1652772699-image14.png)
Dựa vào bảng xét dấu, ta thấy rằng \[f\left( x \right) \le 0 \Leftrightarrow x \in \left( { - \,\infty ; - \,5} \right] \cup \left[ {3; + \,\infty } \right).\]
Đáp án cần chọn là: D
Câu 28:
Bất phương trình : \[\left| {3x - 3} \right| \le \left| {2x + 1} \right|\] có nghiệm là
 Xem đáp án
Xem đáp án
Ta có
\[\left| {3x - 3} \right| \le \left| {2x + 1} \right| \Leftrightarrow {\left| {3x - 3} \right|^2} \le {\left| {2x + 1} \right|^2} \Leftrightarrow {\left( {3x - 3} \right)^2} - {\left( {2x + 1} \right)^2} \le 0\]
\[ \Leftrightarrow \left( {3x - 3 - 2x - 1} \right)\left( {3x - 3 + 2x + 1} \right) \le 0 \Leftrightarrow \left( {x - 4} \right)\left( {5x - 2} \right) \le 0\]
Xét dấu \[\left( {x - 4} \right)\left( {5x - 2} \right)\] ta được:
![Bất phương trình : \[\left| {3x - 3} \right| \le \left| {2x + 1} \right|\] có nghiệm làTa có\[\left| {3x - 3} \right| \le \left| {2x + 1} \right| \Leftrightarrow {\left| {3x - 3} \right|^2} (ảnh 1)](https://video.vietjack.com/upload2/images/1652772499/1652772699-image15.png)
Suy ra \[\frac{2}{5} \le x \le 4\]
Vậy tập nghiệm của bất phương trình là \[S = \left[ {\frac{2}{5};4} \right].\]
Đáp án cần chọn là: C
Câu 29:
Cho biểu thức \[f\left( x \right) = \frac{1}{{3x - 6}}.\] Tập hợp tất cả các giá trị của x để f(x) ≤ 0 là
 Xem đáp án
Xem đáp án
Ta có
\[f\left( x \right) \le 0 \Leftrightarrow \frac{1}{{3x - 6}} \le 0 \Leftrightarrow 3x - 6 < 0 \Leftrightarrow x < 2 \Leftrightarrow x \in \left( { - \,\infty ;2} \right).\]
Đáp án cần chọn là: B
Câu 30:
Cho biểu thức \[f\left( x \right) = \frac{{\left( {x + 3} \right)\left( {2 - x} \right)}}{{x - 1}}.\]. Tập hợp tất cả các giá trị của xx thỏa mãn bất phương trình f(x) >0 là
 Xem đáp án
Xem đáp án
- Ta có \[f\left( x \right) = \frac{{2 - x}}{{x + 1}} + 2 = \frac{{2 - x + 2\left( {x + 1} \right)}}{{x + 1}} = \frac{{x + 4}}{{x + 1}}.\]
Phương trình \[x + 4 = 0 \Leftrightarrow x = - \,4\] và \[x + 1 = 0 \Leftrightarrow x = - \,1.\]
- Bảng xét dấu
![Cho biểu thức \[f\left( x \right) = \frac{{\left( {x + 3} \right)\left( {2 - x} \right)}}{{x - 1}}.\]. Tập hợp tất cả các giá trị của xx thỏa mãn bất phương trình f(x) >0 là- Phương trình\[x (ảnh 1)](https://video.vietjack.com/upload2/images/1652772499/1652772699-image17.png)
Dựa vào bảng xét dấu, ta thấy rằng \[f\left( x \right) < 0 \Leftrightarrow x \in \left( { - \,4; - \,1} \right).\]
Đáp án cần chọn là: C
Câu 31:
Tích của nghiệm nguyên âm lớn nhất và nghiệm nguyên dương nhỏ nhất của bất phương trình \[\left( {3x - 6} \right)\left( {x - 2} \right)\left( {x + 2} \right)\left( {x - 1} \right) >0\] là
 Xem đáp án
Xem đáp án
Bất phương trình
\[\left( {3x - 6} \right)\left( {x - 2} \right)\left( {x + 2} \right)\left( {x - 1} \right) >0 \Leftrightarrow 3{\left( {x - 2} \right)^2}\left( {x + 2} \right)\left( {x - 1} \right) >0\]
Vì \[{\left( {x - 2} \right)^2} >0,\,\,\forall x \ne 2\] nên bất phương trình trở thành\(\left\{ {\begin{array}{*{20}{c}}{x \ne 2}\\{(x + 2)(x - 1) >0}\end{array}} \right.\)
Đặt \[f\left( x \right) = \left( {x + 2} \right)\left( {x - 1} \right).\]
Phương trình \[x + 2 = 0 \Leftrightarrow x = - \,2\] và\[x - 1 = 0 \Leftrightarrow x = 1.\]
Ta có bảng xét dấu
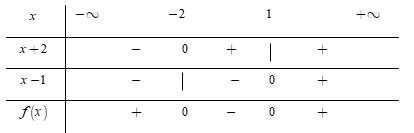
Dựa vào bảng xét dấu, ta thấy rằng \[f\left( x \right) >0 \Leftrightarrow x \in \left( { - \,\infty ; - \,2} \right) \cup \left( {1; + \,\infty } \right).\]
Kết hợp với điều kiện \[x \ne 2,\] ta được\[ \Leftrightarrow x \in \left( { - \,\infty ; - \,2} \right) \cup \left( {1;2} \right) \cup \left( {2; + \,\infty } \right).\]Do đó, nghiệm nguyên âm lớn nhất của bất phương trình là −3 và nghiệm nguyên dương nhỏ nhất của bất phương trình là 3.
Vậy tích cần tính là (−3).3=−9.
Đáp án cần chọn là: A
Câu 32:
Tập nghiệm của bất phương trình \[2x\left( {4 - x} \right)\left( {3 - x} \right)\left( {3 + x} \right) >0\]là
 Xem đáp án
Xem đáp án
Đặt \[f\left( x \right) = 2x\left( {4 - x} \right)\left( {3 - x} \right)\left( {3 + x} \right).\]
Phương trình \[2x = 0 \Leftrightarrow x = 0;\,\,4 - x = 0 \Leftrightarrow x = 4;\,\,\]
Và\[3 - x = 0 \Leftrightarrow x = 3;3 + x = 0 \Leftrightarrow x = - 3\]
Ta có bảng xét dấu:
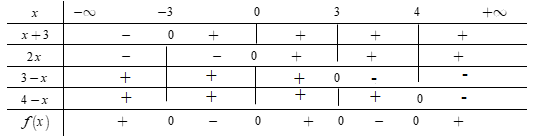
Từ bảng xét dấu ta có
\[f(x) >0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x >4}\\{0 < x < 3}\\{x < - 3}\end{array}} \right. \Leftrightarrow x \in ( - \infty ; - 3) \cup (0;3) \cup (4; + \infty ).\]
Suy ra tập nghiệm bất phương trình là hợp của ba khoảng.
Đáp án cần chọn là: C
Câu 33:
Nghiệm nguyên nhỏ nhất thỏa mãn bất phương trình \[\left( {x - 1} \right)\sqrt {x\left( {x + 2} \right)} \ge 0\]là
 Xem đáp án
Xem đáp án
Điều kiện:\[x\left( {x + 2} \right) \ge 0\]
Đặt \[f\left( x \right) = x\left( {x + 2} \right).\]Phương trình x = 0 và \[x + 2 = 0 \Leftrightarrow x = - \,2.\]
Bảng xét dấu:
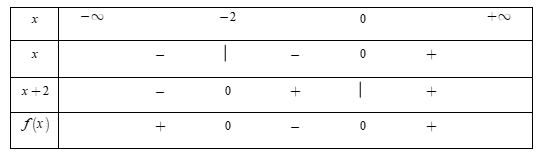
Dựa vào bảng xét dấu, ta thấy rằng \[f(x) \ge 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x \ge 0}\\{x \le - 2}\end{array}} \right.\]
- Nếu\[f(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = - 2}\end{array}} \right.\] thì bất phương trình trở thành \[0 \ge 0\] (đúng).
- Nếu \(\left[ {\begin{array}{*{20}{c}}{x >0}\\{x < - 2}\end{array}} \right.\) ta được \[x \ge 1\]
Vậy bất phương trình có tập nghiệm \[S = \left\{ { - 2} \right\} \cup \left\{ 0 \right\} \cup \left[ {1; + \infty } \right)\]Do đó nghiệm nguyên nhỏ nhất của bất phương trình là x = −2.
Đáp án cần chọn là: A
Câu 34:
Tập nghiệm của bất phương trình \[\frac{{{x^2} + x - 3}}{{{x^2} - 4}} \ge 1\] là
 Xem đáp án
Xem đáp án
Bất phương trình
\[\frac{{{x^2} + x - 3}}{{{x^2} - 4}} \ge 1 \Leftrightarrow \frac{{{x^2} + x - 3}}{{{x^2} - 4}} - 1 \ge 0 \Leftrightarrow \frac{{x + 1}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} \ge 0.\]
Đặt \[f\left( x \right) = \frac{{x + 1}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}.\]Ta có\[x + 1 = 0 \Leftrightarrow x = - \,1\]và
\[(x - 2)(x + 2) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - 2}\\{x = 2}\end{array}} \right.\]
Bảng xét dấu
![Tập nghiệm của bất phương trình \[\frac{{{x^2} + x - 3}}{{{x^2} - 4}} \ge 1\] làBất phương trình\[\frac{{{x^2} + x - 3}}{{{x^2} - 4}} \ge 1 \Leftrightarrow \frac{{{x^2} + x - 3}}{{{x^2} - 4} (ảnh 1)](https://video.vietjack.com/upload2/images/1652772499/1652772699-image22.png)
Dựa vào bảng xét dấu, ta thấy rằng \[f(x) \ge 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{ - 2 < x \le - 1}\\{x >2}\end{array}} \right.\]Vậy tập nghiệm của bất phương trình là\[S = \left( { - \,2; - \,1} \right] \cup \left( {2; + \,\infty } \right).\]
Đáp án cần chọn là: B
Câu 35:
Bất phương trình \[\frac{4}{{x - 1}} - \frac{2}{{x + 1}} < 0\]có tập nghiệm là
 Xem đáp án
Xem đáp án
Bất phương trình \[\frac{4}{{x - 1}} - \frac{2}{{x + 1}} < 0 \Leftrightarrow \frac{{2x + 6}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} < 0.\]
Đặt \[f\left( x \right) = \frac{{2x + 6}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}.\]
Ta có \[2x + 6 = 0 \Leftrightarrow x = - \,3\]và\[(x - 1)(x + 1) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x = - 1}\end{array}} \right.\]
Bảng xét dấu
![Bất phương trình \[\frac{4}{{x - 1}} - \frac{2}{{x + 1}} < 0\]có tập nghiệm làBất phương trình \[\frac{4}{{x - 1}} - \frac{2}{{x + 1}} < 0 \Leftrightarrow \frac{{2x + 6}}{{\left( {x - 1} \ri (ảnh 1)](https://video.vietjack.com/upload2/images/1652772499/1652772699-image23.png)
Dựa vào bảng xét dấu, ta thấy rằng \[f(x) < 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x < - 3}\\{ - 1 < x < 1}\end{array}} \right.\]
Vậy tập nghiệm của bất phương trình là \[S = \left( { - \,\infty ; - \,3} \right) \cup \left( { - \,1;1} \right).\]
Đáp án cần chọn là: B
Câu 36:
Nghiệm của bất phương trình \[\left| {2x - 3} \right| \le 1\]là
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
Câu 37:
Bất phương trình \[\frac{{x + 4}}{{{x^2} - 9}} - \frac{2}{{x + 3}} < \frac{{4x}}{{3x - {x^2}}}\] có nghiệm nguyên lớn nhất là
 Xem đáp án
Xem đáp án
Bất phương trình tương đương với
\[\frac{{x\left( {x + 4} \right)}}{{x\left( {x - 3} \right)\left( {x + 3} \right)}} - \frac{{2x\left( {x - 3} \right)}}{{x\left( {x - 3} \right)\left( {x + 3} \right)}} < - \frac{{4x\left( {x + 3} \right)}}{{x\left( {x - 3} \right)\left( {x + 3} \right)}} \Leftrightarrow \frac{{3x + 22}}{{\left( {x - 3} \right)\left( {x + 3} \right)}} < 0.\]
Đặt \[f\left( x \right) = \frac{{3x + 22}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}.\]
Ta có \[3x + 22 = 0 \Leftrightarrow x = - \frac{{22}}{3};\left\{ {\begin{array}{*{20}{c}}{x - 3 = 0 \Leftrightarrow x = 3}\\{x + 3 = 0 \Leftrightarrow x = - 3}\end{array}} \right.\]
Bảng xét dấu
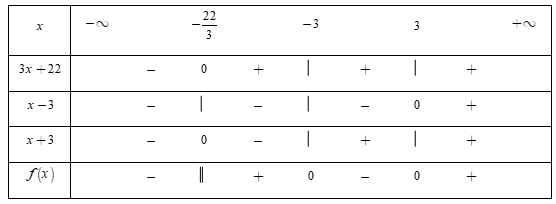
Dựa vào bảng xét dấu, ta thấy rằng\[f\left( x \right) < 0 \Leftrightarrow x \in \left( { - \,\infty ; - \frac{{22}}{3}} \right) \cup \left( { - \,3;3} \right).\]
Vậy nghiệm nguyên lớn nhất thỏa mãn bất phương trình là x = 2.
Đáp án cần chọn là: A
Câu 38:
Tập nghiệm của bất phương trình \[\left| {5x - 4} \right| \ge 6\]có dạng \[S = ( - \infty ;a] \cup [b; + \infty ).\;\] Tính tổng \[P = 5a + b.\].
 Xem đáp án
Xem đáp án
Bất phương trình
\[|5x - 4| \ge 6 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{5x - 4 \ge 6}\\{5x - 4 \le - 6}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{5x \ge 10}\\{5x \le - 2}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x \ge 2}\\{x \le - \frac{2}{5}}\end{array}} \right.\]
Do đó, tập nghiệm của bất phương trình là \[S = \left( { - \,\infty ; - \frac{2}{5}} \right] \cup \left[ {2; + \,\infty } \right).\]
Mà\[S = \left( { - \,\infty ;a} \right] \cup \left[ {b; + \,\infty } \right)\] nên\(\left\{ {\begin{array}{*{20}{c}}{a = - \frac{2}{5}}\\{b = 2}\end{array}} \right.\)
Vậy \[P = 5a + b = 5.\left( { - \frac{2}{5}} \right) + 2 = 0\]Đáp án cần chọn là: C
Câu 39:
Hỏi có bao nhiêu giá trị nguyên x trong \[\left[ { - 2017;2017} \right]\;\]thỏa mãn bất phương trình \[|2x + 1| < 3x\;\]?
 Xem đáp án
Xem đáp án
TH1. Với \[2x + 1 \ge 0 \Leftrightarrow x \ge - \frac{1}{2},\]khi đó\[\left| {2x + 1} \right| < 3x \Leftrightarrow 2x + 1 < 3x \Leftrightarrow x >1.\]</>
Kết hợp với điều kiện \[x \ge - \frac{1}{2}\]suy ra \[{S_1} = \left( {1; + \,\infty } \right).\]
TH2. Với\[2x + 1 < 0 \Leftrightarrow x < - \frac{1}{2},\]khi đó\[\left| {2x + 1} \right| < 3x \Leftrightarrow - \,2x - 1 < 3x \Leftrightarrow x >- \frac{1}{5}.\]</>
Kết hợp với điều kiện \[x < - \frac{1}{2}\]suy ra \[{S_2} = \emptyset .\]
Suy ra tập nghiệm của bất phương trình là \[S = {S_1} \cup {S_2} = \left( {1; + \,\infty } \right).\]
Mà \[x \in \left[ { - 2017;2017} \right]\]nên\[x \in \left( {1;2017} \right]\]hay\[x \in \left\{ {2;3;...;2017} \right\}\]
Vậy có 2016 giá trị nguyên của x thỏa mãn.
Đáp án cần chọn là: A
Câu 40:
Số nghiệm nguyên thỏa mãn bất phương trình \[\left| {x + 2} \right| + \left| { - 2x + 1} \right| \le x + 1\]là
 Xem đáp án
Xem đáp án
Xét bất phương trình \[\left| {x + 2} \right| + \left| { - \,2x + 1} \right| \le x + 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( * \right).\]
Bảng xét dấu
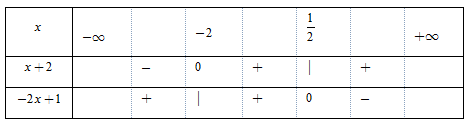
TH1. Với x < −2, khi đó\[\left( * \right) \Leftrightarrow \left( { - \,x - 2} \right) + \left( { - \,2x + 1} \right) \le x + 1\]
\[ \Leftrightarrow - \,2 \le 4x \Leftrightarrow x \ge - \frac{1}{2}.\]
Kết hợp với điều kiện x<−2, ta được tập nghiệm \[{S_1} = \emptyset .\]
TH2. Với \[ - \,2 \le x < \frac{1}{2},\]khi đó \[\left( * \right) \Leftrightarrow x + 2 - 2x + 1 \le x + 1\]
\[ \Leftrightarrow 2x \ge 2 \Leftrightarrow x \ge 1.\]
Kết hợp với điều kiện \[ - \,2 \le x < \frac{1}{2},\]ta được tập nghiệm\[{S_2} = \emptyset .\]
TH3. Với \[x \ge \frac{1}{2},\]khi đó\[\left( * \right) \Leftrightarrow x + 2 - \left( { - 2x + 1} \right) \le x + 1 \Leftrightarrow 2x \le 0 \Leftrightarrow x \le 0.\]
Kết hợp với điều kiện \[x \ge \frac{1}{2},\]ta được tập nghiệm\[{S_3} = \emptyset .\]
Vậy tập nghiệm của bất phương trình là \[S = {S_1} \cup {S_2} \cup {S_3} = \emptyset .\]
Đáp án cần chọn là: D
Câu 41:
Bất phương trình \[\left| {x + 2} \right| - \left| {x - 1} \right| < x - \frac{3}{2}\]có tập nghiệm là
 Xem đáp án
Xem đáp án
Xét bất phương trình\[\left| {x + 2} \right| - \left| {x - 1} \right| \le x - \frac{3}{2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( * \right).\]
Lập bảng xét dấu
![Bất phương trình \[\left| {x + 2} \right| - \left| {x - 1} \right| < x - \frac{3}{2}\]có tập nghiệm làXét bất phương trình\[\left| {x + 2} \right| - \left| {x - 1} \right| \le x - \frac{3}{2 (ảnh 1)](https://video.vietjack.com/upload2/images/1652772499/1652772699-image27.png)
TH1. Với x < −2, khi đó\[\left( * \right) \Leftrightarrow - \,x - 2 + x - 1 < x - \frac{3}{2} \Leftrightarrow x >- \frac{3}{2}.\]</>
Kết hợp với điều kiện x < −2, ta được tập nghiệm \[{S_1} = \emptyset .\]
TH2. Với\[ - \,2 \le x < 1,\] khi đó \[\left( * \right) \Leftrightarrow x + 2 + x - 1 < x - \frac{3}{2} \Leftrightarrow x < - \frac{5}{2}.\]
Kết hợp với điều kiện \[ - \,2 \le x < 1,\] ta được tập nghiệm\[{S_2} = \emptyset .\]
TH3. Với \[x \ge 1,\] khi đó\[\left( * \right) \Leftrightarrow x + 2 - x + 1 < x - \frac{3}{2} \Leftrightarrow x >\frac{9}{2}.\]</>
Kết hợp với điều kiện \[x \ge 1,\] ta được tập nghiệm \[{S_3} = \left( {\frac{9}{2}; + \,\infty } \right).\]
Vậy tập nghiệm của bất phương trình là \[S = {S_1} \cup {S_2} \cup {S_3} = \left( {\frac{9}{2}; + \,\infty } \right).\]
Đáp án cần chọn là: D
Câu 42:
Bạn An chọn một số nguyên, nhân số đó với 4 rồi trừ đi 30. Lấy kết quả có được nhân với 2 và cuối cùng trừ đi 10 thì được một số có hai chữ số. Số lớn nhất An có thể chọn được có hàng đơn vị bằng:
 Xem đáp án
Xem đáp án
Gọi số nguyên lớn nhất bạn An có thể chọn là \[x\left( {x \in \mathbb{Z}} \right)\]
Theo bài ra ta có \[2\left( {4x - 30} \right) - 10\] là số có 2 chữ số.
\( \Rightarrow \left[ {\begin{array}{*{20}{c}}{10 \le 2(4x - 30) - 10 \le 99}\\{ - 99 \le 2(4x - 30) - 10 \le - 10}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{20 \le 2(4x - 30) \le 109}\\{ - 89 \le 2(4x - 30) \le 0}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{10 \le 4x - 30 \le \frac{{109}}{2}}\\{ - \frac{{89}}{2} \le 4x - 30 \le 0}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{40 \le 4x \le \frac{{169}}{2}}\\{ - \frac{{29}}{2} \le 4x \le 30}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{10 \le x \le \frac{{169}}{8}}\\{ - \frac{{29}}{8} \le x \le \frac{{30}}{4}}\end{array}} \right.\)
Vì \[x \in \mathbb{Z}\] và x là số lớn nhất nên x=21.
Vậy số lớn nhất An có thể chọn có hàng đơn vị bằng 1.
Đáp án cần chọn là: C
