Hai đường thẳng vuông góc
-
375 lượt thi
-
21 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Trong không gian cho ba đường thẳng phân biệt a,b,c. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
A sai vì: Nếu a và b cùng vuông góc với c thì a và b hoặc song song hoặc chéo nhau hoặc cắt nhau (cùng nằm trong mặt phẳng vuông góc với c)
C sai vì: Giả sử hai đường thẳng a và b chéo nhau, ta dựng đường thẳng c là đường vuông góc chung của a và b. Khi đó góc giữa a và c bằng với góc giữa b và c và cùng bằng 900, nhưng hiển nhiên hai đường thẳng a và b không song song.
D sai vì: Giả sử a vuông góc với c,b song song với c, khi đó góc giữa a và c bằng 900, còn góc giữa b và c bằng 00.
Do đó B đúng.
Đáp án cần chọn là: B
Câu 2:
Trong các mệnh đề sau, mệnh đề nào đúng?
 Xem đáp án
Xem đáp án
Đáp án A sai vì nếu góc giữa hai véc tơ chỉ phương lớn hơn 900 thì góc giữa hai đường thẳng sẽ là góc bù với góc đó chứ không bằng.
Đáp án B sai vì vẫn có thể xảy ra các trường hợp b và c chéo nhau, cắt nhau, trùng nhau.
Đáp án C sai vì góc giữa hai đường thẳng có thể nhọn hoặc vuông.
Do đó D đúng.
Đáp án cần chọn là: D
Câu 3:
Cho tứ diện đều ABCD. Số đo góc giữa hai đường thẳng AB và CD bằng:
 Xem đáp án
Xem đáp án
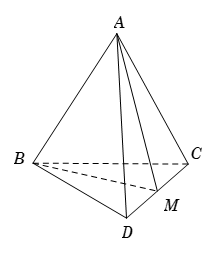
Gọi M là trung điểm của CD.
Ta có\[\overrightarrow {CD} .\overrightarrow {AM} = \vec 0\] và\[\overrightarrow {CD} .\overrightarrow {MB} = \vec 0\]
Do đó\[\overrightarrow {CD} .\overrightarrow {AB} = \overrightarrow {CD} .\left( {\overrightarrow {AM} + \overrightarrow {MB} } \right) = \overrightarrow {CD} .\overrightarrow {AM} + \overrightarrow {CD} .\overrightarrow {MB} = \vec 0\]
Suy ra\[AB \bot CD\] nên số đo góc giữa hai đường thẳng AB và CD bằng 900.
Đáp án cần chọn là: C
Câu 4:
Trong các mệnh đề sau đây, mệnh đề nào là đúng?
 Xem đáp án
Xem đáp án
Ta có:\(\left\{ {\begin{array}{*{20}{c}}{a \bot b}\\{b//c}\end{array}} \right. \Rightarrow a \bot c\) nên đáp án C đúng.
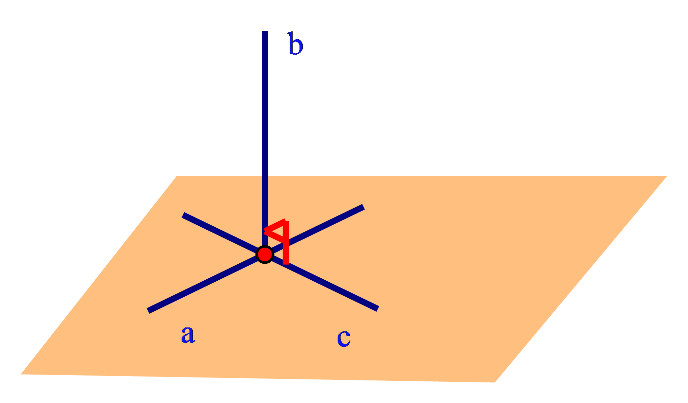
Đán án A: Ta thấy b cùng vuông góc với a và c nhưng hai đường thẳng a,c không vuông góc với nhau
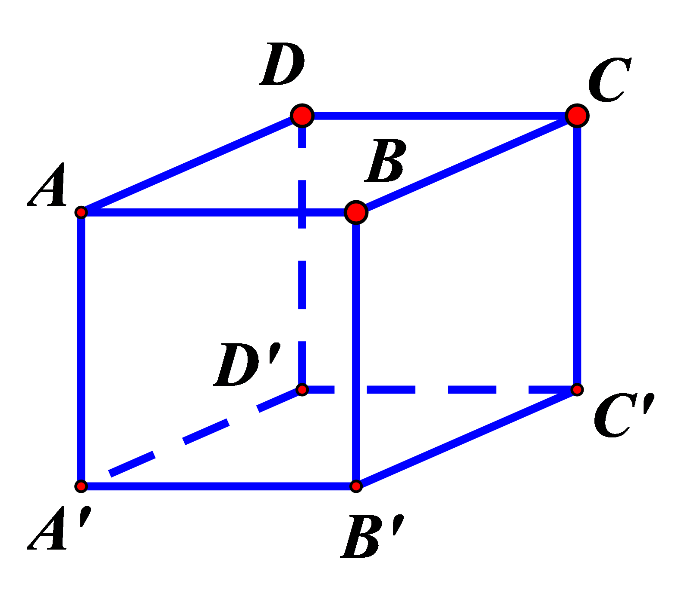
Đáp án B: AB và BC và BB' vuông góc với nhau từng đôi một. BD cũng vuông góc với BB' nhưng lại không vuông góc với AB và cũng không vuông góc với BC.
Đáp án D: Ta thấy đường thẳng AD và BC song song, đường thẳng AB vuông góc với AD nhưng không vuông góc với mọi đường thẳng nằm trong mặt phẳng (ABCD)
Đáp án cần chọn là: C
Câu 5:
Cho tứ diện ABCD có \[AB = AC = AD\;\] và \[\widehat {BAC} = \widehat {BAD} = {60^0}\] Hãy xác định góc giữa cặp vectơ \(\overrightarrow {AB} \)và \(\overrightarrow {CD} \)?
 Xem đáp án
Xem đáp án
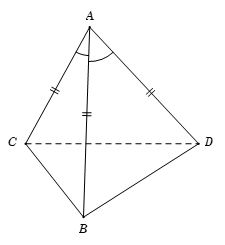
Ta có\[\overrightarrow {AB} .\overrightarrow {CD} = \overrightarrow {AB} .\left( {\overrightarrow {AD} - \overrightarrow {AC} } \right) = \overrightarrow {AB} .\overrightarrow {AD} - \overrightarrow {AB} .\overrightarrow {AC} \]
\[\begin{array}{*{20}{l}}{ = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|.\cos \left( {\overrightarrow {AB} .\overrightarrow {AD} } \right) - \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AB} .\overrightarrow {AC} } \right)}\\{ = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|.\cos {{60}^ \circ } - \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos {{60}^ \circ }.}\end{array}\]
Mà \[AC = AD \Rightarrow \overrightarrow {AB} .\overrightarrow {CD} = 0 \Rightarrow \left( {\overrightarrow {AB} ,\overrightarrow {CD} } \right) = {90^ \circ }\]
Đáp án cần chọn là: D
Câu 6:
Cho hình chóp S.ABC có SA=SB và CA=CB. Tính số đo của góc giữa hai đường thẳng chéo nhau SC và AB.
 Xem đáp án
Xem đáp án
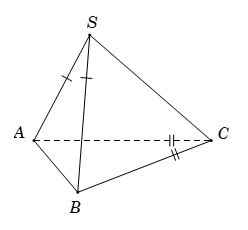
Xét \[\overrightarrow {SC} .\overrightarrow {AB} = - \overrightarrow {CS} .\left( {\overrightarrow {CB} - \overrightarrow {CA} } \right) = \overrightarrow {CS} .\overrightarrow {CA} - \overrightarrow {CS} .\overrightarrow {CB} \]
\[ = CS.CA.\cos \widehat {SCA} - CS.CB.\cos \widehat {SCB}\]
Do \[{\rm{\Delta }}SAC = {\rm{\Delta }}SBC\left( {c.c.c} \right)\]nên\[\widehat {SCA} = \widehat {SCB} \Rightarrow \cos \widehat {SCA} = \cos \widehat {SCB}\]
Do đó\[CS.CA.\cos \widehat {SCA} - CS.CB.\cos \widehat {SCB} = 0\](do \[CA = CB\]) hay\[\overrightarrow {SC} .\overrightarrow {AB} = 0\]
Vậy \[SC \bot AB\]
Đáp án cần chọn là: DCâu 7. Mệnh đề nào sau đây là đúng?
A.Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc thì song song với đường thẳng còn lại.
B.Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau
C.Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau
D.Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia
Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
Đáp án cần chọn là: D
Câu 7:
Cho tứ diện ABCD có \[AB = CD = a,{\rm{IJ}} = \frac{{a\sqrt 3 }}{2}\] (I, J lần lượt là trung điểm của BC và AD). Số đo góc giữa hai đường thẳng AB và CD là
 Xem đáp án
Xem đáp án
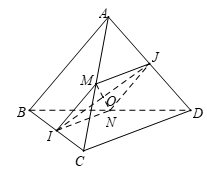
Gọi M, N lần lượt là trung điểm AC, BD.
Ta có:
\(\left\{ {\begin{array}{*{20}{c}}{MI = NI = \frac{1}{2}AB = \frac{1}{2}CD = \frac{a}{2}}\\{MI\;//\;AB\;//\;NJ,MJ//CD//IN}\end{array}} \right. \Rightarrow MINJ\)là hình thoi.
Gọi O là giao điểm của MN và IJ.
Ta có:\[\widehat {MIN} = 2\widehat {MIO}\]
Xét\[{\rm{\Delta }}MIO\]vuông tại O, ta có:
\[\cos \widehat {MIO} = \frac{{IO}}{{MI}} = \frac{{\frac{{a\sqrt 3 }}{4}}}{{\frac{a}{2}}} = \frac{{\sqrt 3 }}{2} \Rightarrow \widehat {MIO} = {30^ \circ } \Rightarrow \widehat {MIN} = {60^ \circ }\]
Mà:\[\left( {AB,CD} \right) = \left( {IM,IN} \right) = \widehat {MIN} = {60^ \circ }\]
Đáp án cần chọn là: C
Câu 8:
Cho hình hộp ABCD.A′B′C′D′. Giả sử tam giác AB′C và A′DC′ đều có 3 góc nhọn. Góc giữa hai đường thẳng AC và A′D là góc nào sau đây?
 Xem đáp án
Xem đáp án
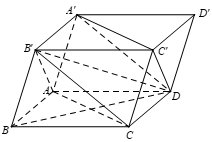
Ta có: \[AC//A'C'\](tính chất của hình hộp)
\[ \Rightarrow \left( {AC,A'D} \right) = \left( {A'C',A'D} \right) = \widehat {DA'C'}\] (do giả thiết cho\[{\rm{\Delta }}DA'C'\]nhọn).
Đáp án cần chọn là: D
Câu 9:
Cho hình lập phương ABCD.EFGH Hãy xác định góc giữa cặp vectơ \(\overrightarrow {AB} \)và \(\overrightarrow {DH} \)?
 Xem đáp án
Xem đáp án
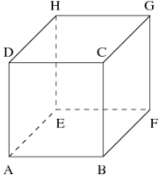
\(\left. {\begin{array}{*{20}{c}}{AB \bot AE}\\{AE//DH}\end{array}} \right\} \Rightarrow AB \bot DH \Rightarrow \widehat {\left( {AB,DH} \right)} = {90^ \circ }\)
Đáp án cần chọn là: B
Câu 10:
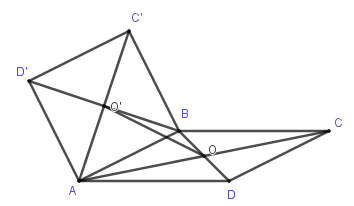
Trong không gian cho hai hình vuông ABCD và ABC′D′ có chung cạnh AB và nằm trong hai mặt phẳng khác nhau, lần lượt có tâm O và O′. Hãy xác định góc giữa cặp vectơ \(\overrightarrow {AB} \)và \[\overrightarrow {{\rm{OO}}'} ?\]
 Xem đáp án
Xem đáp án
Do O,O′ là tâm các hình vuông ABCD,ABC′D′ nên O,O′ là trung điểm của BD,BD′.
Do đó OO′ là đường trung bình của tam giác\[BDD' \Rightarrow \overrightarrow {OO'} = \frac{1}{2}\overrightarrow {DD'} \]
Ta có:
\[\overrightarrow {AB} .\overrightarrow {OO'} = \overrightarrow {AB} .\frac{1}{2}\overrightarrow {DD'} = \frac{1}{2}.\overrightarrow {AB} \left( {\overrightarrow {AD'} - \overrightarrow {AD} } \right)\]
\[ = \frac{1}{2}\overrightarrow {AB} .\overrightarrow {AD'} - \frac{1}{2}\overrightarrow {AB} .\overrightarrow {AD} = 0 - 0 = 0\]
Do đó góc giữa\[\overrightarrow {AB} \]và\[\overrightarrow {OO'} \]bằng\[{90^0}\]
Đáp án cần chọn là: D
Câu 11:
Cho tứ diện ABCD có AB=AC=AD và \(\widehat {BAC} = \widehat {BAD} = {60^0}\). Gọi I và J lần lượt là trung điểm của AB và CD. Hãy xác định góc giữa cặp vectơ \(\overrightarrow {{\rm{IJ}}} \)và \(\overrightarrow {CD} ?\)
 Xem đáp án
Xem đáp án
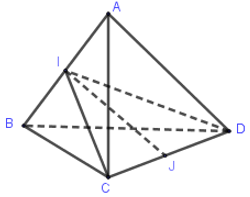
Ta có BAC và BAD là 2 tam giác đều, I là trung điểm của AB nên CI=DI (2 đường trung tuyến của 2 tam giác đều chung cạnh AB) nên CID là tam giác cân ở I. Do đó \[IJ \bot CD\]
Đáp án cần chọn là: B
Câu 12:
Cho tứ diện ABCD có \(AC = \frac{3}{2}AD;\widehat {CAB} = \widehat {DAB} = {60^0};CD = AD\). Gọi \[\varphi \] là góc giữa AB và CD. Chọn khẳng định đúng?
 Xem đáp án
Xem đáp án
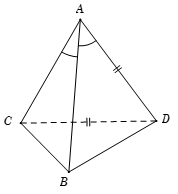
Ta có \[\cos \left( {AB,CD} \right) = \frac{{\left| {\overrightarrow {AB} .\overrightarrow {CD} } \right|}}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {CD} } \right|}} = \frac{{\left| {\overrightarrow {AB} .\overrightarrow {CD} } \right|}}{{AB.CD}}\]
Mặt khác\[\overrightarrow {AB} .\overrightarrow {CD} = \overrightarrow {AB} \left( {\overrightarrow {AD} - \overrightarrow {AC} } \right) = \overrightarrow {AB} .\overrightarrow {AD} - \overrightarrow {AB} .\overrightarrow {AC} \]
\[\begin{array}{*{20}{l}}{ = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|.\cos \left( {\overrightarrow {AB} .\overrightarrow {AD} } \right) - \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AB} .\overrightarrow {AC} } \right)}\\{ = AB.AD.\cos {{60}^ \circ } - AB.AC.\cos {{60}^ \circ }}\\{ = AB.AD.\frac{1}{2} - AB.\frac{3}{2}AD.\frac{1}{2} = - \frac{1}{4}AB.AD = - \frac{1}{4}AB.CD.}\end{array}\]
Do có\[\cos \left( {AB,CD} \right) = \frac{{\left| { - \frac{1}{4}AB.CD} \right|}}{{AB.CD}} = \frac{1}{4}\]
Vậy\[\cos \varphi = \frac{1}{4}\]
Đáp án cần chọn là: D
Câu 13:
Cho tứ diện ABCD có trọng tâm G. Chọn khẳng định đúng?
 Xem đáp án
Xem đáp án
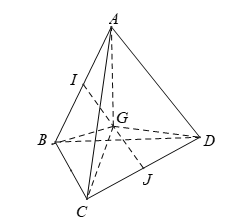
\[\begin{array}{*{20}{l}}{A{B^2} + A{C^2} + A{D^2} + B{C^2} + B{D^2} + C{D^2}}\\{ = {{\left( {\overrightarrow {AG} + \overrightarrow {GB} } \right)}^2} + {{\left( {\overrightarrow {AG} + \overrightarrow {GC} } \right)}^2} + {{\left( {\overrightarrow {AG} + \overrightarrow {GD} } \right)}^2} + {{\left( {\overrightarrow {BG} + \overrightarrow {GC} } \right)}^2} + {{\left( {\overrightarrow {BG} + \overrightarrow {GD} } \right)}^2} + {{\left( {\overrightarrow {CG} + \overrightarrow {GD} } \right)}^2}}\end{array}\]\[\begin{array}{l} = 3A{G^2} + 3B{G^2} + 3C{G^2} + 3D{G^2} + 2\overrightarrow {AG} .\overrightarrow {GB} \\ + 2\overrightarrow {AG} .\overrightarrow {GC} + 2\overrightarrow {AG} .\overrightarrow {GD} + 2\overrightarrow {BG} .\overrightarrow {GD} + 2\overrightarrow {BG} .\overrightarrow {GD} + 2\overrightarrow {CG} .\overrightarrow {GD} \left( 1 \right)\end{array}\]
Lại có:
\[\begin{array}{*{20}{l}}{\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {G{\rm{D}}} = \vec 0 \Leftrightarrow {{\left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {G{\rm{D}}} } \right)}^2} = 0}\\\begin{array}{l} \Leftrightarrow G{A^2} + G{B^2} + G{C^2} + G{{\rm{D}}^2} = 2\overrightarrow {AG} .\overrightarrow {GB} \\ + 2\overrightarrow {AG} .\overrightarrow {GC} + 2\overrightarrow {AG} .\overrightarrow {GD} + 2\overrightarrow {BG} .\overrightarrow {GD} + 2\overrightarrow {BG} .\overrightarrow {GD} + 2\overrightarrow {CG} .\overrightarrow {GD} \left( 2 \right)\end{array}\end{array}\]
Từ (1) và (2) suy ra
\[A{B^2} + A{C^2} + A{D^2} + B{C^2} + B{D^2} + C{D^2} = 4\left( {G{A^2} + G{B^2} + G{C^2} + G{D^2}} \right)\]
Đáp án cần chọn là: B
Câu 14:
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng a. Gọi M và N lần lượt là trung điểm của AD và SD. Số đo của góc (MN,SC) bằng:
 Xem đáp án
Xem đáp án
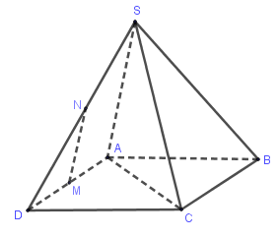
Ta có: \[AC = a\sqrt 2 \]
\[ \Rightarrow A{C^2} = 2{a^2} = S{A^2} + S{C^2}\]
\[ \Rightarrow {\rm{\Delta }}SAC\] vuông tại S.
Khi đó:\[\overrightarrow {NM} .\overrightarrow {SC} = \frac{1}{2}\overrightarrow {SA} .\overrightarrow {SC} = 0 \Leftrightarrow \left( {\overrightarrow {NM} ,\overrightarrow {SC} } \right) = {90^ \circ }\]
\[ \Rightarrow \left( {MN,SC} \right) = {90^ \circ }\]
Đáp án cần chọn là: C
Câu 15:
Cho hình lập phương ABCD.A′B′C′D′. Chọn khẳng định sai?
 Xem đáp án
Xem đáp án
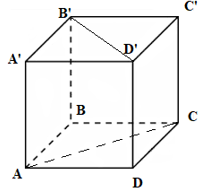
Ta có:\[\overrightarrow {AA'} .\overrightarrow {B'D'} = \overrightarrow {BB'} .\overrightarrow {BD} = \overrightarrow {BB'} .\left( {\overrightarrow {BA} + \overrightarrow {BC} } \right)\]
\[ = \overrightarrow {BB'} .\overrightarrow {BA} + \overrightarrow {BB'} .\overrightarrow {BC} = 0\]
(vì\[\left( {\overrightarrow {BB'} ,\overrightarrow {BA} } \right) = {90^0}\] và\[\left( {\overrightarrow {BB'} ,\overrightarrow {BC} } \right) = {90^0}\])
Do đó: \[\left( {\overrightarrow {AA'} ,\overrightarrow {B'D'} } \right) = {90^0} \Rightarrow \widehat {\left( {AA',B'D'} \right)} = {90^0}\]
Đáp án cần chọn là: B
Câu 16:
Cho \[\left| {\vec a} \right| = 3,\left| {\vec b} \right| = 5\], góc giữa \(\overrightarrow a \)và \(\overrightarrow b \)bằng\({120^0}\). Chọn khẳng định sai trong các khẳng định sau?
 Xem đáp án
Xem đáp án
\[ = {\left| {\vec a} \right|^2} + {\left| {\vec b} \right|^2} + 2.\left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,\vec b} \right) = {3^2} + {5^2} + 2.3.5.\left( { - \frac{1}{2}} \right) = 19\]
Do đó\[\left| {\vec a + \vec b} \right| = \sqrt {19} \]
Đáp án B:\[{\left| {\vec a - \vec b} \right|^2} = {\left( {\vec a - \vec b} \right)^2} = {\vec a^2} - 2\vec a\vec b + {\vec b^2}\]
\[ = {\left| {\vec a} \right|^2} - 2.\left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,\vec b} \right) + {\left| {\vec b} \right|^2} = {3^2} - 2.3.5.\left( { - \frac{1}{2}} \right) + {5^2} = 49\]
\[ \Rightarrow \left| {\vec a - \vec b} \right| = 7\]nên B đúng.
Đáp án C:\[{\left| {\vec a - 2\vec b} \right|^2} = {\left( {\vec a - 2\vec b} \right)^2} = {\vec a^2} - 4\vec a\vec b + 4{\vec b^2}\]
\[ = {\left| {\vec a} \right|^2} - 4\left| {\vec a} \right|\left| {\vec b} \right|\cos \left( {\vec a,\vec b} \right) + 4{\left| {\vec b} \right|^2} = {3^2} - 4.3.5.\left( { - \frac{1}{2}} \right) + {4.5^2} = 139\]
\[ \Rightarrow \left| {\vec a - 2\vec b} \right| = \sqrt {139} \]nên C đúng.
Đáp án D:\[{\left| {\vec a + 2\vec b} \right|^2} = {\left( {\vec a + 2\vec b} \right)^2} = {\vec a^2} + 4\vec a\vec b + 4{\vec b^2}\]
\[ = {\left| {\vec a} \right|^2} + 4\left| {\vec a} \right|\left| {\vec b} \right|\cos \left( {\vec a,\vec b} \right) + 4{\left| {\vec b} \right|^2} = {3^2} + 4.3.5.\left( { - \frac{1}{2}} \right) + {4.5^2} = 79\]
\[ \Rightarrow \left| {\vec a + 2\vec b} \right| = \sqrt {79} \]nên D sai.
Đáp án cần chọn là: D
Câu 17:
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vectơ \[\overrightarrow {AF} \]và \(\overrightarrow {EG} \)?
 Xem đáp án
Xem đáp án
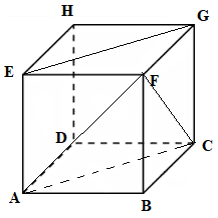
Ta có:
\[\begin{array}{l}\overrightarrow {{\rm{AF}}} = \overrightarrow {AB} + \overrightarrow {AE} \\\overrightarrow {EG} = \overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \end{array}\]
\[ \Rightarrow \overrightarrow {{\rm{AF}}} .\overrightarrow {EG} = \left( {\overrightarrow {AB} + \overrightarrow {AE} } \right).\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) = A{B^2} + \overrightarrow {AE} .\overrightarrow {AB} + \overrightarrow {AB} .\overrightarrow {AD} + \overrightarrow {AE} .\overrightarrow {AD} = A{B^2}\]
\( \Rightarrow \cos \left( {\overrightarrow {AF} ,\overrightarrow {EG} } \right) = \frac{{\overrightarrow {AF} .\overrightarrow {EG} }}{{\left| {\overrightarrow {AF} } \right|.\left| {\overrightarrow {EG} } \right|}} = \frac{{{a^2}}}{{a\sqrt 2 .a\sqrt 2 }} = \frac{1}{2}\)
\( \Rightarrow \widehat {\left( {\overrightarrow {AF} ,\overrightarrow {EG} } \right)} = {60^ \circ }\)
Đáp án cần chọn là: B
Câu 18:
Cho hình hộp ABCD.A′B′C′D′ có tất cả các cạnh đều bằng nhau. Trong các mệnh đề sau, mệnh đề nào có thể sai?
 Xem đáp án
Xem đáp án
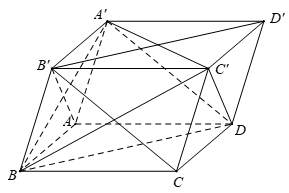
A đúng vì:
\(\left\{ {\begin{array}{*{20}{c}}{A\prime C\prime \bot B\prime D\prime }\\{B\prime D\prime //BD}\end{array}} \right. \Rightarrow A\prime C\prime \bot BD\)
C đúng vì:\(\left\{ {\begin{array}{*{20}{c}}{A\prime B \bot AB'}\\{AB\prime //DC\prime }\end{array}} \right. \Rightarrow A\prime B \bot DC\prime \)
D đúng vì:\(\left\{ {\begin{array}{*{20}{c}}{BC\prime \bot B\prime C}\\{B\prime C//A\prime D}\end{array}} \right. \Rightarrow BC\prime \bot A\prime D\)
Đáp án cần chọn là: B
Câu 19:
Cho tứ diện ABCD có AB vuông góc với CD. Mặt phẳng (P) song song với AB và CD lần lượt cắt BC,DB,AD,AC tại M,N,P,Q. Tứ giác MNPQ là hình gì?
 Xem đáp án
Xem đáp án
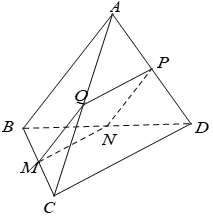
Ta có\(\left\{ {\begin{array}{*{20}{c}}{(MNPQ)//AB}\\{(MNPQ) \cap (ABC) = MQ}\end{array}} \right. \Rightarrow MQ//AB\)
Tương tự ta có:\[MN//CD,\,\,NP//AB,\,\,QP//C{\rm{D}}\]
Do đó tứ giác MNPQ là hình bình hành
lại có\[MN \bot MQ\left( {do\,AB \bot CD\,} \right)\]
Vậy tứ giác MNPQ là hình chữ nhật.
Đáp án cần chọn là: C
Câu 20:
Cho tứ diện ABCD có AB vuông góc với CD, AB=CD=6. M là điểm thuộc cạnh BC sao cho \[MC = x.BC(0 < x < 1)\] Mặt phẳng(P) song song với AB và CD lần lượt cắt BC,DB,AD,AC tại M,N,P,Q. Diện tích lớn nhất của tứ giác bằng bao nhiêu?
 Xem đáp án
Xem đáp án
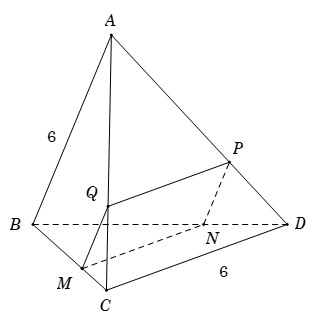
Xét tứ giác MNPQ có\(\left\{ {\begin{array}{*{20}{c}}{MQ//NP//AB}\\{MN//PQ//CD}\end{array}} \right. \Rightarrow MNPQ\) là hình bình hành.
Mặt khác, \[AB \bot CD \Rightarrow MQ \bot MN\] Do đó, MNPQ là hình chữ nhật.
Vì \[MQ//AB\] nên \[\frac{{MQ}}{{AB}} = \frac{{CM}}{{CB}} = x \Rightarrow MQ = x.AB = 6x\]
Theo giả thiết\[MC = x.BC \Rightarrow BM = \left( {1 - x} \right)BC\]
Vì \[MN//CD\] nên\[\frac{{MN}}{{CD}} = \frac{{BM}}{{BC}} = 1 - x \Rightarrow MN = \left( {1 - x} \right).CD = 6\left( {1 - x} \right)\]
Diện tích hình chữ nhật MNPQ là
\[{S_{MNPQ}} = MN.MQ = 6\left( {1 - x} \right).6x = 36.x.\left( {1 - x} \right) \le 36{\left( {\frac{{x + 1 - x}}{2}} \right)^2} = 9\]
Ta có \[{S_{MNPQ}} = 9\] khi\[x = 1 - x \Leftrightarrow x = \frac{1}{2}\]Vậy diện tích tứ giác MNPQ lớn nhất bằng 9 khi M là trung điểm của BC.
Đáp án cần chọn là: A
Câu 21:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a. Hình chiếu vuông góc của S trên mặt phẳng (ABCD) trùng với trung điểm H của cạnh AB. Biết tam giác SAB là tam giác đều. Số đo của góc giữa SA và CD là
 Xem đáp án
Xem đáp án
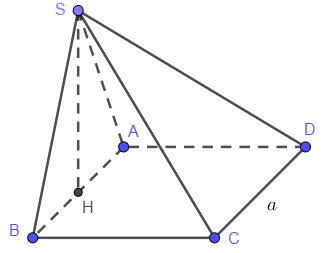
Bước 1:
\[CD||AB \Rightarrow \widehat {\left( {SA,CD} \right)} = \widehat {\left( {SA,AB} \right)} = \widehat {SAB}\]
Bước 2:
Vì tam giác SAB là tam giác đều.
\[ \Rightarrow \widehat {SAB} = {60^ \circ }\]
Vậy góc giữa SA và CD là \[{60^0}\]
Đáp án cần chọn là: A
