Số phức, các phép toán với số phức
-
1484 lượt thi
-
44 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Số phức \[z = a + bi\;\] có phần thực là:
 Xem đáp án
Xem đáp án
Phần thực của số phức z là a.
Đáp án cần chọn là: A
Câu 2:
Số phức \[z = \sqrt 2 i - 1\] có phần thực là:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Câu 3:
Hai số phức \[z = a + bi,z' = a + b'i\] bằng nhau nếu:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
Câu 4:
Số phức liên hợp của số phức \[z = a - bi\] là:
 Xem đáp án
Xem đáp án
Số phức liên hợp của số phức \[z = a - bi\] là \[\bar z = a + bi\].
Đáp án cần chọn là: B
Câu 5:
Chọn mệnh đề đúng:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Câu 6:
Gọi M,N lần lượt là các điểm biểu diễn số phức \[z = a + bi\] và \[z\prime = a\prime + b\prime i\]. Chọn câu đúng:
 Xem đáp án
Xem đáp án
Điểm M biểu diễn số phức \[z = a + bi\] nên M(a;b)
Điểm N biểu diễn số phức \[z' = a' + b'i\] nên N(a′;b′)
Đáp án cần chọn là: C
Câu 7:
Cho hai số phức \[z = a + bi,z' = a' + b'i\]. Chọn công thức đúng:
 Xem đáp án
Xem đáp án
Ta có:
\[z + z' = \left( {a + bi} \right) + \left( {a' + b'i} \right) = \left( {a + a'} \right) + \left( {b + b'} \right)i\]
\[z - z' = \left( {a + bi} \right) - \left( {a' + b'i} \right) = \left( {a - a'} \right) + \left( {b - b'} \right)i\]
\[z.z' = \left( {a + bi} \right)\left( {a' + b'i} \right) = \left( {aa' - bb'} \right) + \left( {ab' + a'b} \right)i\]
Vậy C đúng.
Đáp án cần chọn là: C
Câu 8:
Cho số phức \[z = a + bi\] và\(\overline z \)là số phức liên hợp của z. Chọn kết luận đúng:
 Xem đáp án
Xem đáp án
Ta có:\[z = a + bi \Rightarrow \bar z = a - bi \Rightarrow z + \bar z = 2a;z - \bar z = 2bi;z.\bar z = {a^2} + {b^2}\]
Do đó A đúng.
Đáp án cần chọn là: A
Câu 9:
Tìm số phức có phần thực bằng 12 và mô đun bằng 13:
 Xem đáp án
Xem đáp án
Ta có: \[{\left| z \right|^2} = {a^2} + {b^2} \Leftrightarrow {b^2} = {\left| z \right|^2} - {a^2} \Leftrightarrow b = \pm \sqrt {{{\left| z \right|}^2} - {a^2}} \]
Vậy phần ảo của số phức đó là\[b = \pm \sqrt {{{13}^2} - {{12}^2}} = \pm 5\]Đáp án cần chọn là: C
Câu 10:
Cho số phức \[z = a + bi(ab \ne 0)\] Tìm phần thực của số phức \[w = \frac{1}{{{z^2}}}.\]
 Xem đáp án
Xem đáp án
\[z = a + bi \Rightarrow {z^2} = {\left( {a + bi} \right)^2} = {a^2} + 2abi + {b^2}{i^2} = {a^2} - {b^2} + 2abi\]
\[w = \frac{1}{{{{\left( {a + bi} \right)}^2}}} = \frac{1}{{{a^2} - {b^2} + 2abi}} = \frac{{{a^2} - {b^2} - 2abi}}{{\left( {{a^2} - {b^2} + 2abi} \right)\left( {{a^2} - {b^2} - 2abi} \right)}} = \frac{{{a^2} - {b^2} - 2abi}}{{{{\left( {{a^2} - {b^2}} \right)}^2} - {{\left( {2abi} \right)}^2}}}\]\[ = \frac{{{a^2} - {b^2} - 2abi}}{{{a^4} + {b^4} - 2{a^2}{b^2} - 4{a^2}{b^2}{i^2}}} = \frac{{{a^2} - {b^2} - 2abi}}{{{a^4} + {b^4} - 2{a^2}{b^2} + 4{a^2}{b^2}}} = \frac{{{a^2} - {b^2} - 2abi}}{{{a^4} + {b^4} + 2{a^2}{b^2}}}\]
\[ = \frac{{{a^2} - {b^2} - 2abi}}{{{{\left( {{a^2} + {b^2}} \right)}^2}}} = \frac{{{a^2} - {b^2}}}{{{{\left( {{a^2} + {b^2}} \right)}^2}}} - \frac{{2ab}}{{{{\left( {{a^2} + {b^2}} \right)}^2}}}i\]
Nên phần thực của số phức w là : \[\frac{{{a^2} - {b^2}}}{{{{\left( {{a^2} + {b^2}} \right)}^2}}}\]
Đáp án cần chọn là: D
Câu 11:
Cho số phức \[z = 3 - 2i\]. Tìm phần thực và phần ảo của số phức \(\overline z \)
 Xem đáp án
Xem đáp án
Số phức liên hợp của z là 3+2i, phần thực 3, phần ảo 2.
Đáp án cần chọn là: D
Câu 12:
Cho hai số phức \[{z_1} = 1 + i\] và \[{z_2} = 2 - 3i\]. Tính môđun của số phức \[{z_1} + {z_2}\;\].
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Câu 13:
Cho số phức \[z = 1 + \sqrt 3 i\]. Khi đó
 Xem đáp án
Xem đáp án
Ta có:\[z = 1 + \sqrt 3 i \Rightarrow \frac{1}{z} = \frac{1}{{1 + \sqrt 3 i}} = \frac{{1 - \sqrt 3 i}}{{(1 - \sqrt 3 i)(1 + \sqrt 3 i)}}\]
\[ = \frac{{1 - \sqrt 3 i}}{{{1^2} - {{(\sqrt 3 i)}^2}}} = \frac{{1 - \sqrt 3 i}}{4} = \frac{1}{4} - \frac{{\sqrt 3 }}{4}i\]
Đáp án cần chọn là: D
Câu 14:
Cho số phức \[z = \frac{{7 - 11i}}{{2 - i}}\]. Tìm phần thực và phần ảo của \(\overline z \)
 Xem đáp án
Xem đáp án
\[z = \frac{{7 - 11i}}{{2 - i}} = \frac{{(7 - 11i)(2 + i)}}{{{2^2} + {1^2}}} = \frac{{14 + 11 + 7i - 22i}}{5} = \frac{{25 - 15i}}{5} = 5 - 3i \Rightarrow \bar z = 5 + 3i\]
Vậy phần thực và phần ảo của \[\bar z\] là 5 và 3.
Đáp án cần chọn là: C
Câu 15:
Cho 2 số phức,\[{z_1} = 1 + 3i,\overline z 2 = 4 + 2i.\] Tính môđun của số phức \[{z_2} - 2{z_1}\]
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Câu 16:
Cho số phức \[z = 2 + 3i\]. Tìm số phức \[{\rm{w}} = (3 + 2i)z + 2\bar z\]
 Xem đáp án
Xem đáp án
\[{\rm{w}} = (3 + 2i)z + 2\bar z = (3 + 2i)(2 + 3i) + 2.(2 - 3i)\]
\[ = 6 - 6 + 4i + 9i + 4 - 6i = 4 + 7i\]
Đáp án cần chọn là: B
Câu 17:
Tính môđun của số phức z biết \[\bar z = \left( {4 - 3i} \right)\left( {1 + i} \right)\]
 Xem đáp án
Xem đáp án
Ta có:
\[\bar z = \left( {4 - 3i} \right)\left( {1 + i} \right) = 7 + i \Rightarrow z = 7 - i \Rightarrow \left| z \right| = \sqrt {50} = 5\sqrt 2 \]
Đáp án cần chọn là: C
Câu 18:
Xét số phức z thỏa mãn \[\left| {z + 2 - i} \right| + \left| {z - 4 - 7i} \right| = 6\sqrt 2 \]. Gọi m,M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của \[\left| {z - 1 + i} \right|.\]Tính P=m+M.
 Xem đáp án
Xem đáp án
Gọi \[z = x + yi\left( {x,y \in R} \right)\]
Trên mặt phẳng tọa độ Oxy gọi P(x;y) là điểm biểu diễn của số phức z
Gọi \[A\left( { - 2;1} \right),B\left( {4;7} \right)\]thì
\[\begin{array}{*{20}{l}}{AB = 6\sqrt 2 = \left| {z + 2 - i} \right| + \left| {z - 4 - 7i} \right|}\\{ = \sqrt {{{\left( {x + 2} \right)}^2} + {{\left( {y - 1} \right)}^2}} + \sqrt {{{\left( {x - 4} \right)}^2} + {{\left( {y - 7} \right)}^2}} = PA + PB}\end{array}\]
Suy ra tập hợp các điểm P thỏa mãn chính là đoạn thẳng AB
Có\[\left| {z - 1 + i} \right| = \sqrt {{{\left( {x - 1} \right)}^2} + {{\left( {y + 1} \right)}^2}} = PC\]với C(1;−1)
Do đó\[P{C_{\min }}\]khi P là hình chiếu của C lên AB và \[P{C_{\max }}\] khi\[P \equiv B\]
Suy ra \[M = CB = \sqrt {73} \]
Ta có:\[AB:\frac{{x + 2}}{{4 + 2}} = \frac{{y - 1}}{{7 - 1}} \Leftrightarrow x - y + 3 = 0\]
\[ \Rightarrow m = d\left( {C,AB} \right) = \frac{{\left| {1 - \left( { - 1} \right) + 3} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }} = \frac{5}{{\sqrt 2 }}\]
\[ \Rightarrow M + m = \frac{{5\sqrt 2 + 2\sqrt {73} }}{2}\]
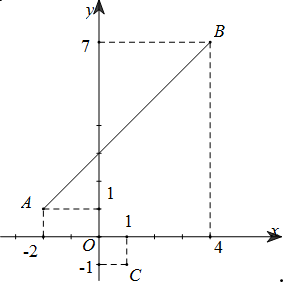
Đáp án cần chọn là: B
Câu 19:
Cho số phức \[z = 1 + i + {i^2} + {i^3} + ... + {i^9}\]. Khi đó:
 Xem đáp án
Xem đáp án
\[z = 1 + i + {i^2} + {i^3} + ... + {i^9} = 1 + i - 1 - i + 1 + i - 1 - i + 1 + i = 1 + i\]
Đáp án cần chọn là: B
Câu 20:
Trong các số phức \[{z_1} = - 2i,\,\,{z_2} = 2 - i,\,\,{z_3} = 5i,\,\,{z_4} = 4\] có bao nhiêu số thuần ảo?
 Xem đáp án
Xem đáp án
Có 2 số thuần ảo, đó là: \[{z_1} = - 2i,\,\,\,{z_3} = 5i\]
Đáp án cần chọn là: D
Câu 21:
Có bao nhiêu số phức z thỏa mãn \[|z| = 1\;\]và \[\mid {z^3} + 2024z + \overline z \mid - 2\sqrt 3 \mid z + \overline z \mid = 2019\]
 Xem đáp án
Xem đáp án
Ta có :
\[\mid {z^3} + 2024z + \overline z \mid - 2\sqrt 3 \mid z + \overline z \mid = 2019\]
\[\begin{array}{l} \Leftrightarrow \mid \frac{{\mid {z^3} + 2024z + \overline z \mid }}{{|z|}} - 2\sqrt 3 \mid z + \overline z \mid = 2019\\ \Leftrightarrow \mid {z^2} + 2024 + \frac{{\overline z }}{z}\mid - 2\sqrt 3 \mid z + \overline z \mid = 2019\\ \Leftrightarrow \left| {{z^2} + 2024 + {z^{ - 2}}} \right| - 2\sqrt 3 \mid z + \overline z \mid = 2019\\ \Leftrightarrow \left| {{{\left( {z + \overline z } \right)}^2} - 2z\overline z + 2021} \right| - 2\sqrt 3 \mid z + \overline z \mid = 2019\\ \Leftrightarrow \left| {{{(z + \overline z )}^2} + 2022\mid } \right| - 2\sqrt 3 \mid z + \overline z \mid = 2019\end{array}\]
Đặt\[z = a + bi \Rightarrow \bar z = a - bi \Rightarrow z + \bar z = 2a\]
Khi đó phương trình cuối trở thành
\[\left| {{{\left( {2a} \right)}^2} + 2022} \right| - 2\sqrt 3 .\left| {2a} \right| = 2019 \Leftrightarrow 4{a^2} - 4\sqrt 3 \left| a \right| + 3 = 0\]
\[ \Leftrightarrow {\left( {2\left| a \right| - \sqrt 3 } \right)^2} = 0 \Leftrightarrow \left| a \right| = \frac{{\sqrt 3 }}{2} \Leftrightarrow a = \pm \frac{{\sqrt 3 }}{2}\]
Mà
\[\left| z \right| = 1 \Leftrightarrow {\left| z \right|^2} = 1 \Leftrightarrow {a^2} + {b^2} = 1 \Rightarrow {b^2} = 1 - {a^2} = \frac{1}{4} \Leftrightarrow b = \pm \frac{1}{2}\]
Vậy có bốn số phức thỏa mãn bài toán là
\[{z_1} = \frac{{\sqrt 3 }}{2} + \frac{1}{2}i,\,\,{z_2} = \frac{{\sqrt 3 }}{2} - \frac{1}{2}i,\,\,{z_3} = - \frac{{\sqrt 3 }}{2} - \frac{1}{2}i,\,\,{z_4} = - \frac{{\sqrt 3 }}{2} + \frac{1}{2}i.\]
Đáp án cần chọn là: B
Câu 22:
Tìm các số thực x,y thỏa mãn đẳng thức \[3x + y + 5xi = 2y - (x - y)i.\]
 Xem đáp án
Xem đáp án
Ta có:
\[\begin{array}{l}3x + y + 5xi = 2y - (x - y)i\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{3x + y = 2y}\\{5x = - (x - y)}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{3x - y = 0}\\{6x - y = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 0}\\{y = 0}\end{array}} \right.\end{array}\]
Đáp án cần chọn là: D
Câu 23:
Cho \[{z_1} = 2 + i;\,\,{z_2} = 1 - 3i.\]. Tính \[A = {\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2}.\]
 Xem đáp án
Xem đáp án
Ta có:\(\left\{ {\begin{array}{*{20}{c}}{{z_1} = 2 + i}\\{{z_2} = 1 - 3i}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}}{|{z_1}{|^2} = {2^2} + 1 = 5}\\{|{z_2}{|^2} = 1 + {{( - 3)}^2} = 10}\end{array} \Rightarrow {{\left| {{z_1}} \right|}^2} + {{\left| {{z_2}} \right|}^2} = 15.} \right.\)
Đáp án cần chọn là: D
Câu 24:
Cho số phức \[z = 3 - 4i.\] Modun của z bằng
 Xem đáp án
Xem đáp án
Modun của số phức\[z = 3 - 4i\] là: \[\left| z \right| = \sqrt {{3^2} + {{\left( { - 4} \right)}^2}} = 5.\]
Đáp án cần chọn là: D
Câu 25:
Tính môđun của số phức \[w = {\left( {1 - i} \right)^2}z\], biết số phức z có môđun bằng m.
 Xem đáp án
Xem đáp án
Ta có\[\left| w \right| = \left| {{{\left( {1 - i} \right)}^2}z} \right| = \left| {{{\left( {1 - i} \right)}^2}} \right|.\left| z \right|\]
\[ = {\left| {1 - i} \right|^2}.\left| z \right| = {\left( {\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} } \right)^2}.\left| z \right| = 2\left| z \right| = 2m\] vì\[\left| z \right| = m\]
Đáp án cần chọn là: A
Câu 26:
Cho hai số phức \[{z_1},\,\,{z_2}\] thỏa mãn \[{z_1}\overline {.{z_1}} = 4,\left| {{z_2}} \right| = 3\]. Giá trị biểu thức \[P = {\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2}\;\] bằng:
 Xem đáp án
Xem đáp án
Ta có\[{z_1}.\overline {{z_1}} = 4 \Rightarrow {\left| {{z_1}} \right|^2} = 4\]
Vậy \[P = {\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2} = 4 + {3^2} = 13\]Đáp án cần chọn là: A
Câu 27:
Cho các số phức \[{z_1} = 3i,{z_2} = m - 2i\]. Số giá trị nguyên của m để \[\left| {{z_2}} \right| < \left| {{z_1}} \right|\;\]là
 Xem đáp án
Xem đáp án
Ta có\[{z_1} = 3i;{z_2} = m - 2i \Rightarrow \left\{ {\begin{array}{*{20}{c}}{|{z_1}| = 3}\\{|{z_2}| = \sqrt {{m^2} + 4} }\end{array}} \right.\]
Mà
\[\left| {{z_2}} \right| < \left| {{z_1}} \right| \Rightarrow \sqrt {{m^2} + 4} < 3 \Leftrightarrow {m^2} + 4 < 9 \Leftrightarrow - \sqrt 5 < m < \sqrt 5 .\]</>
Mặt khác\[m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 2; - 1;0;1;2} \right\}.\]
Có 5 giá trị của m thỏa mãn yêu cầu bài toán.
Đáp án cần chọn là: B
Câu 28:
Cho hai số phức \[{z_1} = 1 + 2i\] và \[{z_2} = 2 - 3i\]. Phần ảo của số phức \[w = 3{z_1} - 2{z_2}\;\] là
 Xem đáp án
Xem đáp án
Ta có\(\left\{ {\begin{array}{*{20}{c}}{{z_1} = 1 + 2i}\\{{z_2} = 2 - 3i}\end{array}} \right. \Rightarrow w = 3{z_1} - 2{z_2} = - 1 + 12i\)
Khi đó phần ảo của số phức w là 12.
Đáp án cần chọn là: C
Câu 29:
Cho số phức z thỏa mãn \[2iz + \overline z = 1 - i.\]Phần thực của số phức z là:
 Xem đáp án
Xem đáp án
Đặt\[z = a + bi\,\,\left( {a,b \in \mathbb{R}} \right) \Rightarrow \bar z = a - bi\]
Khi đó ta có:
\[2iz + \overline z = 1 - i\]
\[ \Leftrightarrow 2i(a + bi) + a - bi = 1 - i\]
\[ \Leftrightarrow 2ai - 2b + a - bi = 1 - i\]
\[ \Leftrightarrow (a - 2b) + (2a - b)i = 1 - i\]
\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{a - 2b = 1}\\{2a - b = - 1}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}}{a = - 1}\\{b = - 1}\end{array}} \right.\)
\[ \Rightarrow z = - 1 - i\]
Vậy phần thực số phức z là −1.
Đáp án cần chọn là: D
Câu 30:
Cho số phức \[z = - \frac{1}{2} + \frac{{\sqrt 3 }}{2}i\]. Số phức \[1 + z + \[z = {m^2} - 3m + 3 + \left( {m - 2} \right)i\left( {m \in \mathbb{R}} \right)\]{z^2}\;\] bằng:
 Xem đáp án
Xem đáp án
Sử dụng MTCT ta có:
![Cho số phức z=− 1/2 + căn bậc 2 của 3/2 i. Số phức 1+z+\[z=^2−3m+3+(m−2)i(m thuộc R){z^2}\;\] bằng: (ảnh 1)](https://video.vietjack.com/upload2/images/1656468560/1656468784-image2.png)
Đáp án cần chọn là: A
Câu 31:
Biết rằng là một số thực. Giá trị của biểu thức \[1 + z + {z^2} + ... + {z^{2019}}\] bằng
 Xem đáp án
Xem đáp án
Vì\[z = {m^2} - 3m + 3 + \left( {m - 2} \right)i\]là số thực nên\[m - 2 = 0 \Leftrightarrow m = 2.\]
Suy ra\[z = {m^2} - 3m + 3 = 1.\]
Vậy \[1 + z + {z^2} + ... + {z^{2019}} = 1 + 1 + 1 + ... + 1 = 2020\](có 2020 số 1).
Đáp án cần chọn là: D
Câu 32:
Số phức liên hợp của số phức \[z = \frac{1}{{1 + i}}\] là:
 Xem đáp án
Xem đáp án
Ta có \[z = \frac{1}{{1 + i}} = \frac{{1 - i}}{{\left( {1 + i} \right)\left( {1 - i} \right)}} = \frac{{1 - i}}{{1 - {i^2}}} = \frac{{1 - i}}{{1 + 1}} = \frac{{1 - i}}{2} = \frac{1}{2} - \frac{1}{2}i\]
\[ \Rightarrow \bar z = \frac{1}{2} + \frac{1}{2}i\]
Đáp án cần chọn là: A
Câu 33:
Số phức nghịch đảo của \[z = 3 + 4i\] là:
 Xem đáp án
Xem đáp án
Số phức nghịch đảo của số phức\[z = 3 + 4i\] là:
\[\frac{1}{{3 + 4i}} = \frac{{3 - 4i}}{{{3^2} - {{\left( {4i} \right)}^2}}} = \frac{{3 - 4i}}{{9 + 16}} = \frac{3}{{25}} - \frac{4}{{25}}i.\]
Đáp án cần chọn là: B
Câu 34:
Trên C phương trình \[\frac{2}{{z - 1}} = 1 + i\;\] có nghiệm là:
 Xem đáp án
Xem đáp án
\[\frac{2}{{z - 1}} = 1 + i \Leftrightarrow z - 1 = \frac{2}{{1 + i}} \Leftrightarrow z - 1 = 1 - i \Leftrightarrow z = 2 - i\]
Đáp án cần chọn là: A
Câu 35:
Có bao nhiêu số phức \[z = a + bi\] với a,b tự nhiên thuộc đoạn \[\left[ {2;9} \right]\;\]và tổng a+b chia hết cho 3?
 Xem đáp án
Xem đáp án
Trong đoạn \[\left[ {2;9} \right]\;\]có
+) 3 số chia hết cho 3: \[\left\{ {3;6;9} \right\}\]
+) 2 số chia 3 dư 1: \[\left\{ {4;7} \right\}.\]
+) 3 số chia 3 dư 2: \[\left\{ {2;5;8} \right\}.\]
Để a+b chia hết cho 3 thì
+) Cả 2 số a, b khác nhau đều chia hết cho 3 có \[A_3^2 = 6\] số phức thỏa mãn.
+) Cả 2 số giống nhau đều chia hết cho 3 có 3 số phức thỏa mãn.
+) 1 số chia 3 dư 1 và 1 số chia 3 dư 2: Có \[C_2^1.C_3^1.2! = 12\] số phức thỏa mãn.
Vậy có tất cả 21 số phức thỏa mãn.
Đáp án cần chọn là: C
Câu 36:
Biết 1+i là nghiệm của phương trình \[zi + azi + bz + a = 0(a,b \in \mathbb{R})\;\] ẩn z trên tập số phức. Tìm \[{b^2} - {a^3}\].
 Xem đáp án
Xem đáp án
Vì \[z = 1 + i\] là 1 nghiệm của phương trình\[zi + azi + bz + a = 0\,\,\,\left( {a,b \in \mathbb{R}} \right)\] nên ta có:
\[(1 + i)i + a.(i + 1)i + b(i + 1) + a = 0\]
\[ \Leftrightarrow - 1 + i + a( - 1 + i) + b + bi + a = 0\]
\[ \Leftrightarrow b - 1 + (1 + a + b)i = 0\]
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{b - 1 = 0}\\{1 + a + b = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{b = 1}\\{a = - 2}\end{array}} \right.\)Vậy\[{b^2} - {a^3} = {1^2} - {\left( { - 2} \right)^3} = 9.\]
Đáp án cần chọn là: D
Câu 37:
Có bao nhiêu số phức thỏa mãn \[{z^2} + 2\left( {\bar z} \right) = 0\]
 Xem đáp án
Xem đáp án
Đặt \[z = a + bi \Rightarrow \bar z = a - bi.\]
Khi đó ta có:
\[{z^2} + 2\overline z = 0\]
\[\begin{array}{l} \Leftrightarrow {(a + bi)^2} + 2(a - bi) = 0\\ \Leftrightarrow {a^2} + 2abi + {b^2}{i^2} + 2a - 2bi = 0\\ \Leftrightarrow {a^2} - {b^2} + 2a + (2ab - 2b)i = 0\end{array}\]
\(\begin{array}{l} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{a^2} - {b^2} + 2a = 0}\\{2ab - 2b = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{a^2} - {b^2} + 2a = 0}\\{2b(a - 1) = 0}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{a^2} - {b^2} + 2a = 0}\\{\left[ {\begin{array}{*{20}{c}}{b = 0}\\{a = 1}\end{array}} \right.}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{a = 1}\\{ - {b^2} + 3 = 0}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{b = 0}\\{{a^2} + 2a = 0}\end{array}} \right.}\end{array}} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{a = 1}\\{b = \pm \sqrt 3 }\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{b = 0}\\{\left[ {\begin{array}{*{20}{c}}{a = 0}\\{a = - 2}\end{array}} \right.}\end{array}} \right.}\end{array}} \right.\end{array}\)
\[ \Rightarrow {z_1} = 1 + \sqrt 3 i,{z_2} = 1 - \sqrt 3 i,{z_3} = 0,{z_4} = - 2\]
Vậy có 4 số phức thỏa mãn yêu cầu bài toán.
Đáp án cần chọn là: D
Câu 38:
Với số phức z tùy ý, cho mệnh đề \[\left| { - z} \right| = \left| z \right|;\left| {\overline z } \right| = \left| z \right|;\left| {z + \overline z } \right| = 0;\left| z \right| > 0.\] Số mệnh đề đúng là:
 Xem đáp án
Xem đáp án
+) Đặt \[z = a + bi \Rightarrow - z = - a - bi.\]
Ta có:\[\left| z \right| = \sqrt {{a^2} + {b^2}} ,\,\,\left| { - z} \right| = \sqrt {{{\left( { - a} \right)}^2} + {{\left( { - b} \right)}^2}} \Rightarrow \left| z \right| = \left| { - z} \right|\] là mệnh đề đúng.
+) Đặt \[z = a + bi \Rightarrow \bar z = a - bi.\]
Ta có:\[\left| z \right| = \sqrt {{a^2} + {b^2}} ,\,\,\left| {\bar z} \right| = \sqrt {{a^2} + {{\left( { - b} \right)}^2}} \Rightarrow \left| z \right| = \left| {\bar z} \right|\] là mệnh đề đúng.
+) Đặt\[z = a + bi \Rightarrow \bar z = a - bi \Rightarrow z + \bar z = 2a\]
\[ \Rightarrow \left| {z + \bar z} \right| = \left| {2a} \right| \Rightarrow \left| {z + \bar z} \right| = 0\]là mệnh đề sai.
+) Đặt\[z = a + bi \Rightarrow \left| z \right| = \sqrt {{a^2} + {b^2}} \ge 0 \Rightarrow \left| z \right| > 0\]là mệnh đề sai.
Vậy có 2 mệnh đề đúng.
Đáp án cần chọn là: A
Câu 39:
Cho số phức z thỏa mãn \[\frac{{3 - 4i}}{z} = \frac{{\left( {2 + 3i} \right)\bar z}}{{{{\left| z \right|}^2}}} + 2 + i\], giá trị của \[\left| z \right|\;\]bằng
 Xem đáp án
Xem đáp án
Ta có
\[\begin{array}{*{20}{l}}{\frac{{3 - 4i}}{z} = \frac{{\left( {2 + 3i} \right)\bar z}}{{{{\left| z \right|}^2}}} + 2 + i}\\{ \Leftrightarrow \frac{{3 - 4i}}{z} = \frac{{\left( {2 + 3i} \right)\bar z}}{{z.\bar z}} + 2 + i}\\{ \Leftrightarrow \frac{{3 - 4i}}{z} = \frac{{2 + 3i}}{z} + 2 + i}\\{ \Leftrightarrow 3 - 4i = 2 + 3i + \left( {2 + i} \right).z}\\{ \Leftrightarrow \left( {2 + i} \right).z = 1 - 7i}\\{ \Leftrightarrow z = \frac{{1 - 7i}}{{2 + i}} = - 1 - 3i}\end{array}\]
Vậy\[\left| z \right| = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 3} \right)}^2}} = \sqrt {10} .\]
Đáp án cần chọn là: B
Câu 40:
Biết số phức z thỏa mãn điều kiện \[\frac{{5\left( {\bar z + i} \right)}}{{z + 1}} = 2 - i\]. Mô đun số phức \[w = 1 + z + {z^{2\;}}\] bằng
 Xem đáp án
Xem đáp án
Đặt\[z = a + bi \Rightarrow \bar z = a - bi\]
Theo bài ra ta có:
\[\frac{{5\left( {\bar z + i} \right)}}{{z + 1}} = 2 - i\]
\( \Rightarrow \frac{{5(a - bi + i)}}{{a + bi + 1}} = 2 - i\)
\[ \Leftrightarrow 5[a - (b - 1)i] = (a + 1 + bi)(2 - i)\]
\[ \Leftrightarrow 5a - 5(b - 1)i = 2(a + 1) + b + (2b - a - 1)i\]
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{5a = 2a + 2 + b}\\{5 - 5b = 2b - a - 1}\end{array}} \right. \Rightarrow a = b = 1\)
\[ \Rightarrow z = 1 + i \Rightarrow {z^2} = 2i\]
\[ \Rightarrow w = 1 + z + {z^2} = 1 + 1 + i + 2i = 2 + 3i\]
Vậy \[\left| {\rm{w}} \right| = \sqrt {{2^2} + {3^2}} = \sqrt {13} .\]
Đáp án cần chọn là: C
Câu 41:
Cho số phức \[z = \frac{{m + 3i}}{{1 - i}},\,\,m \in \mathbb{R}\] Số phức \[w = {z^2}\;\] có \[\left| w \right| = 9\;\] khi các giá trị của m là:
 Xem đáp án
Xem đáp án
Ta có:
\[\left| w \right| = 9 \Rightarrow \left| {{z^2}} \right| = 9 \Leftrightarrow {\left| z \right|^2} = 9\]
\[ \Leftrightarrow \left| z \right| = 3 \Leftrightarrow \left| {\frac{{m + 3i}}{{1 - i}}} \right| = 3\]
\[ \Leftrightarrow \frac{{\left| {m + 3i} \right|}}{{\left| {1 - i} \right|}} = 3 \Leftrightarrow \frac{{\left| {m + 3i} \right|}}{{\sqrt 2 }} = 3\]
\[ \Leftrightarrow \left| {m + 3i} \right| = 3\sqrt 2 \Leftrightarrow \sqrt {{m^2} + 9} = 3\sqrt 2 \]
\[ \Leftrightarrow {m^2} + 9 = 18 \Leftrightarrow {m^2} = 9\]
\[ \Leftrightarrow m = \pm 3\]
Đáp án cần chọn là: C
Câu 42:
Tính tổng phần thực của tất cả các số phức \[z \ne 0\] thỏa mãn \[\left( {z + \frac{5}{{|z|}}} \right)i = 7 - z.\]
 Xem đáp án
Xem đáp án
Theo bài ra ta có:
\[\left( {z + \frac{5}{{|z|}}} \right)i = 7 - z. \Leftrightarrow zi + \frac{{5i}}{{|z|}} = 7 - z \Leftrightarrow z(i + 1) = 7 - \frac{{5i}}{{|z|}}\]
\[ \Leftrightarrow 2|z{|^2} = 49 + \frac{{25}}{{|z{|^2}}} \Leftrightarrow 2|z{|^4} - 49|z{|^2} - 25 = 0\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{|z{|^2} = 25(tm)}\\{|z| = - \frac{1}{2}(ktm)}\end{array}} \right. \Leftrightarrow |z| = 5(Do|z| > 0)\)
Thay\[\left| z \right| = 5\]vào biểu thức đề bài ta có:
\[\left( {z + 1} \right)i = 7 - z \Leftrightarrow z\left( {i + 1} \right) = 7 - i \Leftrightarrow z = \frac{{7 - i}}{{i + 1}} = 3 - 4i\]
Đáp án cần chọn là: C
Câu 43:
Cho số phức z có tích phần thực và phần ảo bằng 625. Gọi a là phần thực của số phức \[\frac{z}{{3 + 4i}}\]. Giá trị nhỏ nhất của |a| bằng:
 Xem đáp án
Xem đáp án
Đặt\[z = x + yi\] Theo giả thiết ta có\[xy = 625.\]
Ta có:
\[\begin{array}{*{20}{l}}{\frac{z}{{3 + 4i}} = \frac{{x + yi}}{{3 + 4i}} = \frac{{\left( {x + yi} \right)\left( {3 - 4i} \right)}}{{25}}}\\{\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{3x + 4y + \left( { - 4x + 3y} \right)i}}{{25}}}\\{\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{3x + 4y}}{{25}} + \frac{{ - 4x + 3y}}{{25}}i}\end{array}\]
Số phức\[\frac{z}{{3 + 4i}}\] có phần thực là\[a = \frac{{3x + 4y}}{{25}} \Rightarrow \left| a \right| = \frac{{\left| {3x + 4y} \right|}}{{25}}\]
Ta có:\[xy = 625 \Leftrightarrow y = \frac{{625}}{x} \Rightarrow \left| a \right| = \frac{{\left| {3x + 4.\frac{{625}}{x}} \right|}}{{25}}\]
Vì\[3x,\,\,\frac{{625}}{x}\] cùng dấu nên\[\left| {3x + 4.\frac{{625}}{x}} \right| \ge 2\sqrt {3x.4.\frac{{625}}{x}} = 100\sqrt 3 \]
Vậy\[\left| a \right| \ge 4\sqrt 3 \] Dấu “=” xảy ra \[ \Leftrightarrow 3x = 4.\frac{{625}}{x} \Leftrightarrow x = \pm \frac{{50}}{{\sqrt 3 }}\]
Đáp án cần chọn là: D
Câu 44:
Cho các số phức z và w thỏa mãn \[\left( {3 - i} \right)\left| z \right| = \frac{z}{{w - 1}} + 1 - i\]. Tìm GTLN của \[T = |w + i|\]
 Xem đáp án
Xem đáp án
Dễ dàng kiểm tra z=0 không thỏa mãn\[\left( {3 - i} \right)\left| z \right| = \frac{z}{{w - 1}} + 1 - i\]
Ta có: \[\left( {3 - i} \right)\left| z \right| = \frac{z}{{w - 1}} + 1 - i \Leftrightarrow \frac{z}{{w - 1}} = \left( {3 - i} \right)\left| z \right| + i - 1\]
\[ \Leftrightarrow \frac{z}{{w - 1}} = \left( {3\left| z \right| - 1} \right) + \left( {1 - \left| z \right|} \right)i\]
\[ \Rightarrow \left| {\frac{z}{{w - 1}}} \right| = \sqrt {10{{\left| z \right|}^2} - 8\left| z \right| + 2} \Rightarrow \left| {w - 1} \right| = \sqrt {\frac{{{{\left| z \right|}^2}}}{{10{{\left| z \right|}^2} - 8\left| z \right| + 2}}} \]
Nhận xét: \[T = \left| {w + i} \right| \le \left| {w - 1} \right| + \left| {1 + i} \right| = \frac{1}{{\sqrt {\frac{2}{{{{\left| z \right|}^2}}} - \frac{8}{{\left| z \right|}} + 10} }} + \sqrt 2 \]
\[ = \frac{1}{{\sqrt {2{{\left( {\frac{1}{{\left| z \right|}} - 2} \right)}^2} + 2} }} + \sqrt 2 \le \frac{{3\sqrt 2 }}{2}\]
Dấu “=” xảy ra khi và chỉ khỉ
\(\left\{ {\begin{array}{*{20}{c}}{|z| = \frac{1}{2}}\\{w - 1 = k(1 + i)}\\{(3 - i)|z| = \frac{z}{{w - 1}} + 1 - i}\end{array}} \right.(k > 0)\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{|z| = \frac{1}{2}}\\{w - 1 = k(1 + i)}\\{(3 - i)\frac{1}{2} = \frac{z}{{k(1 + i)}} + 1 - i}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{|z| = \frac{1}{2}}\\{w - 1 = k(1 + i)}\\{z = \frac{{1 + i}}{2}.\frac{{2k}}{{1 - i}}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{|z| = \frac{1}{2}}\\{w - 1 = k(1 + i)}\\{|z| = k(dok > 0)}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{|z| = \frac{1}{2} = k}\\{w - 1 = \frac{1}{2}(1 + i)}\\{z = \frac{{1 + i}}{2}.\frac{{2k}}{{1 - i}}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{z = \frac{i}{2}}\\{w = \frac{3}{2} + \frac{1}{2}i}\end{array}} \right.\)
Vậy,\[\max T = \frac{{3\sqrt 2 }}{2}\]
Đáp án cần chọn là: B
