Bài 14: Phép cộng và phép trừ số nguyên
-
623 lượt thi
-
57 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
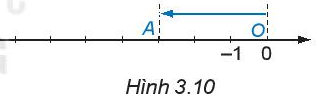
Từ gốc O trên trục số, di chuyển sang trái 3 đơn vị đến điểm A (H.3.10). Điểm A biểu diễn số nào?
 Xem đáp án
Xem đáp án
Vì từ gốc O trên trục số, di chuyển sang trái 3 đơn vị đến điểm A ta được điểm A biểu diễn số -3.
Câu 2:
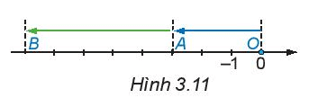
Di chuyển tiếp sang trái thêm 5 đơn vị đến điểm B (H.3.11). B chính là điểm biểu diễn kết quả của phép cộng (-3) + (-5). Điểm B biểu diễn số nào? Từ đó suy ra giá trị của tổng (-3) + (-5).
 Xem đáp án
Xem đáp án
Vì từ điểm A (điểm biểu diễn số -3) di chuyển sang trái 5 đơn vị ta được điểm B. Do đó điểm B biểu diễn số -8.
Mà B chính là điểm biểu diễn kết quả của phép cộng (-3) + (-5) nên (-3) + (-5) = -8
Câu 3:
Thực hiện các phép cộng sau:
(- 12) + (- 48)
(- 236) + (- 1 025)
 Xem đáp án
Xem đáp án
Ta có: (- 12) + (- 48) = - (12 + 48) = -60;
Ta có: (- 236) + (- 1 025) = - (236 + 1 025) = - 1 261.
Câu 4:
Sử dụng phép cộng hai số nguyên âm để giải bài toán sau (H.3.12):
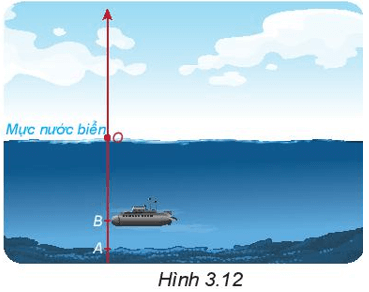
Một chiếc tàu ngầm cần lặn (coi là theo phương thẳng đứng) xuống điểm A dưới đáy biển. Khi tàu đến điểm B ở độ cao – 135 m, máy đo báo rằng tàu còn cách A một khoảng 45 m. Hỏi điểm A nằm ở độ cao bao nhiêu mét?
 Xem đáp án
Xem đáp án
Tàu ở độ cao -135m và còn phải lặn thêm 45m, tức là đi -45m nữa mới đến A. Do đó A nằm ở độ cao:
(-135) + (-45) = - (135 + 45) = - 180 (mét)
Vậy điểm A nằm ở độ cao - 180 mét.
Câu 5:
Tìm số đối của 4; -5; 9; -11.
 Xem đáp án
Xem đáp án
+) Hai điểm 4 và -4 có cùng khoảng cách đến gốc O nên số đối của 4 là -4.
+) Hai điểm 5 và -5 có cùng khoảng cách đến gốc O nên số đối của -5 là 5.
+) Hai điểm 9 và -9 có cùng khoảng cách đến gốc O nên số đối của 9 là -9.
+) Hai điểm 11 và -11 có cùng khoảng cách đến gốc O nên số đối của -11 là 11.
Câu 6:
Tìm số đối của mỗi số 5 và -2 rồi biểu diễn chúng trên cùng một trục số.
 Xem đáp án
Xem đáp án
Số đối của 5 là -5; số đối của -2 là 2.
Biểu diễn trên trục số:
![]()
Câu 7:
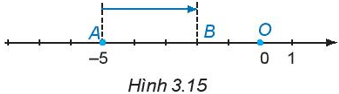
Từ điểm A biểu diễn số - 5 trên trục số di chuyển sang phải 3 đơn vị (H.3.15) đến điểm B. Điểm B biểu diễn kết quả phép cộng nào?
 Xem đáp án
Xem đáp án
Từ điểm A biểu diễn số - 5 trên trục số di chuyển sang phải 3 đơn vị đến điểm B ta được điểm B biểu diễn số -2. Điểm B biểu diễn của phép cộng (-5) + 3.
Câu 8:
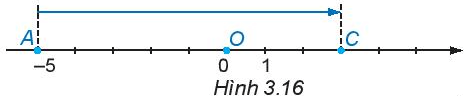
Từ điểm A di chuyển sang phải 8 đơn vị (H.3.16) đến điểm C. Điểm C biểu diễn kết quả của phép cộng nào?
 Xem đáp án
Xem đáp án
Từ điểm A biểu diễn số - 5 trên trục số di chuyển sang phải 8 đơn vị đến điểm C ta được điểm B biểu diễn số 3. Điểm C biểu diễn của phép cộng (-5) + 8.
Câu 9:
Thực hiện các phép tính:
a) 203 + (- 195);
b) (- 137) + 86.
 Xem đáp án
Xem đáp án
a) 203 + (- 195) = 203 - 195 = 8 (do 203 > 195);
b) (- 137) + 86 = - (137 - 86) = - 51 (do 137 > 86).
Câu 10:
Sử dụng phép cộng hai số nguyên khác dấu để giải bài toán sau:
Một máy thăm dò đáy biển ngày hôm trước hoạt động ở độ cao – 946 m (so với mực nước biển). Ngày hôm sau người ta cho máy nổi lên 55 m so với hôm trước. Hỏi ngày hôm sau máy thăm dò đáy biển hoạt động ở độ cao nào?
 Xem đáp án
Xem đáp án
Vì máy nổi lên 55 m so với hôm trước nghĩa là máy di chuyển theo chiều dương
Ngày hôm sau, máy thăm dò hoạt động ở độ cao:
(- 946) + 55 = - (946 -55) = -891 (m)
Vậy ngày hôm sau, máy thăm dò hoạt động ở độ cao -891 m.
Câu 11:

 Xem đáp án
Xem đáp án
Ta có thể đưa ra 1 số ví dụ sau:
Ví dụ 1: Hai số nguyên khác dấu là: 5 và -7.
Khi đó tổng của chúng là 5 + (-7) = -(7 -5) = -2 (do 7 > 2) là số âm
Ví dụ 2: Hai số nguyên khác dấu là: 9 và -4.
Khi đó tổng của chúng là 9 + (-4) = 9 - 4 = 5 (do 9 > 4) là số dương
Ví dụ 3: Hai số nguyên khác dấu là: 4 và -4.
Khi đó tổng của chúng là 4 + (-4) = 0 (đây là tổng của hai số đối nhau)
Từ 3 ví dụ trên, ta nhận thấy tổng của hai số nguyên khác dấu có thể là số âm, có thể là số dương, có thể là 0.
Do vậy không thể kết luận chính xác được là số dương hay số âm.
Câu 12:
Tính và so sánh giá của a + b và b + a với a = - 7, b = 11.
 Xem đáp án
Xem đáp án
Ta có:
a + b = -7 + 11 = 11 – 7 = 4 (do 11 > 7)
b + a = 11 + (-7) = 11 – 7 = 4 (do 11 > 7)
Vì 4 = 4 nên a + b = b + a
Vậy a + b = b + a.
Câu 13:
Tính và so sánh giá trị của (a + b) + c và a + (b + c) với a, b, c
 Xem đáp án
Xem đáp án
(a + b) + c = [2 + (-4)] + (-6)
= - (4 - 2) + (-6) (do 4 > 2)
= - 2 + (-6)
= - (2 + 6) = - 8
a + (b + c) = 2 + [(-4) + (-6)]
= 2 + [-(4 +6)]
= 2 + (-10)
= - (10 - 2) (do 10 > 2)
= - 8
Vì - 8 = - 8 nên (a + b) + c = a + (b + c)
Vậy (a + b) + c = a + (b + c).
Câu 14:
Tính một cách hợp lí:
a) (-2019) + (-550) + (-451)
b) (-2) + 5 + (-6) + 9
 Xem đáp án
Xem đáp án
a) (-2 019) + (-550) + (-451)
= [(-2 019) + (-451)] + (-550) (tính chất giao hoán và kết hợp)
= - (2 019 + 451) + (-550)
= (- 2 470) + (- 550)
= - (2 470 + 550) = - 3 020
b) (-2) + 5 + (-6) + 9
= [(-2) + (-6)] + (5 + 9) (tính chất giao hoán và kết hợp)
= - (2 + 6) +14 = (-8) + 14 = 14 – 8 = 6 (do 14 > 8).
Câu 15:
Nửa tháng đầu một cửa hàng bán lẻ lãi được 5 triệu đồng, nửa tháng sau bị lỗ 2 triệu đồng. Hỏi tháng đó cửa hàng lãi hay lỗ bao nhiêu triệu đồng?
Giải bài toán trên bằng hai cách:
Cách 1. Tính hiệu giữa số tiền lãi và số tiền lỗ.
Cách 2. Hiểu lỗ 2 triệu là “lãi” – 2 triệu để quy về tính tổng của hai số nguyên.
 Xem đáp án
Xem đáp án
Cách 1. Hiệu giữa số tiền lãi và số tiền lỗ là: 5 - 2 = 3 (triệu đồng)
Vậy tháng đó cửa hàng đó lãi 3 triệu đồng.
Cách 2. Lỗ 2 triệu đồng nghĩa là lãi (-2) triệu đồng
Cửa hàng đó lãi: 5 + (-2) = 3 (triệu đồng)
Vậy tháng đó cửa hàng đó lãi 3 triệu đồng.
Câu 16:
Hãy quan sát ba dòng đầu và dự đoán kết quả ở hai dòng cuối:
3 - 1 = 3 + (-1)
3 - 2 = 3 + (-2)
3 - 3 = 3 + (-3)
3 - 4 = ?
3 - 5 = ?
 Xem đáp án
Xem đáp án
Dự đoán: 3 – 4 = 3 +(-4)
3 – 5 = 3 + (-5)
Câu 17:
Tính các hiệu sau:
a) 5 – (-3)
b) (-7) - 8.
 Xem đáp án
Xem đáp án
a) 5 – (-3); = 5 + 3 = 8.
b) (-7) – 8 = (- 7) + (- 8) = - (7 + 8) = -15.
Câu 18:
Nhiệt độ bên ngoài của một máy bay ở độ cao 10 000 m là – . Khi hạ cánh, nhiệt độ ở sân bay là . Hỏi nhiệt độ bên ngoài của máy bay khi ở độ cao 10 000 m và khi hạ cánh chênh lệch bao nhiêu độ C?
 Xem đáp án
Xem đáp án
Nhiệt độ bên ngoài của máy bay ở độ cao 10 000m và khi hạ cánh chênh lệch nhau:
27 - (- 48) = 27 + 48 = 75 ()
Vậy nhiệt độ bên ngoài của máy bay ở độ cao 10 000m và khi hạ cánh chênh lệch nhau .
Câu 19:
Tính tổng hai số cùng dấu:
a) (-7) + (-2);
b) (-8) + (-5);
c) (-11) + (-7);
d) (-6) + (-15).
 Xem đáp án
Xem đáp án
a) (-7) + (-2)
= - (7 + 2) = - 9
b) (-8) + (-5)
= - (8 + 5) = - 13
c) (-11) + (-7)
= - (11 + 7) = - 18
d) (-6) + (-15).
= - (6 + 15) = - 21.
Câu 20:
Tính tổng hai số khác dấu
a) 6 + (-2);
b) 9 + (-3);
c) (-10) + 4;
d) (-1) + 8.
 Xem đáp án
Xem đáp án
a) 6 + (-2)
= 6 – 2 (do 6 > 2)
= 4
b) 9 + (-3)
= 9 – 3 (do 9 > 3)
= 6
c) (-10) + 4
= - (10 - 4) (do 10 > 4)
= - 6
d) (-1) + 8
= 8 – 1 (do 8 > 1)
= 7
Câu 21:
Biểu diễn – 4 và số đối của nó trên cùng một trục số.
 Xem đáp án
Xem đáp án
Số đối của -4 là 4. Ta biểu diễn chúng trên trục số:
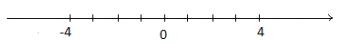
Câu 22:
Thực hiện các phép trừ sau:
a) 9 – (-2)
b) (-7) – 4;
c) 27 – 30;
d) (-63) – ( -15).
 Xem đáp án
Xem đáp án
a) 9 – (-2);
= 9 + 2 = 11
b) ) (-7) – 4
= (-7) + (-4)
= - (7 + 4) = -11
c) 27 – 30;
= 27 + (- 30)
= - (30 – 27) (do 30 > 27)
= - 3
d) (-63) – ( -15)
= (- 63) + 15
= - (63 – 15) (do 63 > 15)
= - 48
Câu 23:
Hai ca nô cùng xuất phát từ C đi về phía A hoặc B như hình vẽ chiều từ C đến B là chiều dương (nghĩa là vận tốc và quãng đường đi từ C về phía B được biểu thị bằng số dương và theo chiều ngược lại là số âm). Hỏi sau một giờ hai ca nô cách nhau bao nhiêu kilomet nếu vận tốc của chúng lần lượt là
a) 11 km/h và 6 km/h?
b) 11 km/h và – 6 km/h?

 Xem đáp án
Xem đáp án
Sau 1 giờ, ca nô có vận tốc 11km/h đi được quãng đường:
11.1 = 11 (km)
Sau 1 giờ, ca nô có vận tốc 6km/h đi được quãng đường:
6.1 = 6 (km)
a) Vì vận tốc của hai ca nô đều dương nên hai ca nô cùng đi về phía B (chiều từ C đến B là dương) nên khoảng cách sau 1 giờ của hai ca nô sẽ là hiệu quãng đường đi được của chúng.
Sau 1 giờ, hiệu quãng đường đi của chúng là:
11 – 6 = 5 (km)
Vậy sau 1 giờ, hiệu quãng đường đi của chúng là 5km.
b) Ca nô có vận tốc 11km/h (là vận tốc dương) nên có chiều đi từ C đến B. Ca nô có vận tốc -6km/h (là vận tốc âm) nên có chiều đi từ C đến A.
Do đó hai ca nô đi ngược chiều nhau, nên khoảng cách sau 1 giờ của hai ca nô sẽ là tổng quãng đường đi được của chúng.
Sau 1 giờ hai ca nô cách nhau:
11 + 6 = 17 (km)
Vậy sau 1 giờ hai ca nô cách nhau 17km.
Câu 24:
Mỗi hình sau đây mô phỏng phép tính nào?
a) 
b) 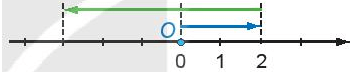
 Xem đáp án
Xem đáp án
a) Hình mô phỏng phép tính: (-5) + 3 hoặc (-5) - (- 3);
b) Hình mô phỏng phép tính: 2 – 5 hoặc 2 + (-5).
Câu 25:
Tính nhẩm:
a) (-3) + (-2);
b) (-8) – 7;
c) (-35) + (-15);
d) 12 – (-8).
 Xem đáp án
Xem đáp án
a) (-3) + (-2)
= - (3 + 2)
= -5
b) (-8) – 7
= (-8) + (-7)
= - (8 + 7)
= - 15
c) (-35) + (-15)
= - (35 + 15)
= - 50
d) 12 – (-8
= 12 + 8
= 20.
Câu 26:
Tính một cách hợp lí:
a) 152 + (-73) – (-18) - 127
b) 7 + 8 + (-9) + (-10).
 Xem đáp án
Xem đáp án
a) 152 + (-73) – (-18) - 127
= [152 - (-18)] - [127 - (-73)]
= (152 + 18) – (127 + 73)
= 170 - 200
= - 30
b) 7 + 8 + (-9) + (-10).
= [(7 + (-9)] + [8 + (-10)]
= (- (9 – 7)] + [- (10 – 8)]
= (-2) + (-2)
= - (2 + 2)
= - 4.
Câu 27:
Tính giá trị của biểu thức (-156) - x, khi:
a) x = -26;
b) x = 76;
c) x = (- 28) – (- 143).
 Xem đáp án
Xem đáp án
a) Thay x = -26 vào biểu thức (-156) - x ta được:
(-156) – x = (-156) – (-26) = (-156) + 26 = - (156 – 26) = - 130. (do 156 > 26)
b) Thay x = 76 vào biểu thức (-156) - x ta được:
(-156) – x = (-156) – 76 = (-156) + (-76) = - (156 + 76) = - 232.
c) Thay x = (- 28) – (- 143) vào biểu thức (-156) - x ta được:
(-156) – x = (-156) – [(-28) – (-143)] = (-156) – [(-28) + 143] = (-156) – (143 – 28) = (- 156) – 115 = (-156) + (-115) = - (156 + 115) = - 271.
Câu 28:
Thay mỗi dấu “*” bằng một chữ số thích hợp để có:
a) ;
b)
 Xem đáp án
Xem đáp án
a)
Vậy dấu * là chữ số 6.
b)
Vậy hai dấu * lần lượt theo thứ tự từ trái qua phải là 7 và 4.
Câu 29:
Tính:
a) (-23) + (-55);
b) 43 + 23;
c) (-234) + (-546).
 Xem đáp án
Xem đáp án
a) (-23) + (-55) = - (23 + 55) = - 78;
b) 43 + 23 = 66;
c) (-234) + (-546) = - (234 + 546) = - 780.
Câu 30:
Tìm số đối của -3; 4; -5; 8; -12.
 Xem đáp án
Xem đáp án
Số đối của – 3 là 3;
Số đối của 4 là -4;
Số đối của – 5 là 5;
Số đối của 8 là – 8;
Số đối của -12 là 12.
Câu 31:
Thực hiện các phép tính:
a) 312 + (-134);
b) (– 254) + 128;
c) 2 304 + (-115).
 Xem đáp án
Xem đáp án
a) 312 + (-134) = 312 – 134 = 178;
b) (– 254) + 128 = - ( 254 – 128) = -128;
c) 2 304 + (-115) = 2 304 – 115 = 2 189.
Câu 32:
Tính một cách hợp lí:
a) (-350) + (-296) + 50 + 96;
b) (-3) + 5 + (-7) + 5.
 Xem đáp án
Xem đáp án
a) (-350) + (-296) + 50 + 96
= [(-350) + 50] + [(-296) + 96]
= (-300) + (-200)
= -500.
b) (-3) + 5 + (-7) + 5
= [(-3) + (-7)] + [5 + 5]
= (-10) + 10
= 0.
Câu 33:
Tính:
a) 15 – 7;
b) 8 – 9;
c) 23 – 154;
d) 12 – 125 – 83.
 Xem đáp án
Xem đáp án
a) 15 – 7 = 8;
b) 8 – 9 = 8 + (-9) = - (9 – 8) = -1;
c) 23 – 154 = - ( 154 – 23) = -131;
d) 12 – 125 – 83
= 12 + (-125) + (-83)
= -(125 – 12) + (-83)
= (-113) + (-83)
= -(113 + 83)
= - 196.
Câu 34:
Bài 1. Nhiệt độ bên ngoài của một máy bay khi bay ở độ cao 1000 m là – 320C. Khi hạ cánh, nhiệt độ ở sân bay là 350C. Hỏi nhiệt độ của máy bay khi ở độ cao 1 000m và khi hạ cánh chênh lệch bao nhiêu độ C?
 Xem đáp án
Xem đáp án
Nhiệt độ của máy bay khi ở độ cao 1 000m và khi hạ cánh chênh lệch:
35 – (-32) = 670C.
Vậy nhiệt độ của máy bay khi ở độ cao 1 000m và khi hạ cánh chênh lệch 670C.
Câu 35:
Tính:
a) (-7) + (-14) + (-6);
b) 9 + (-3) + (-10);
c) 152 + (-73) – (-18) – 127.
 Xem đáp án
Xem đáp án
a) (-7) + (-14) + (-6)
= (-7) + [(-14) + (-6)]
= (-7) + (-20)
= -27
b) 9 + (-3) + (-10)
= [9 + (-3)] + (-10)
= 6 + (-10)
= - (10 – 6)
= - 4
c) 152 + (-73) – (-18) – 127
= 152 + (-73) + 18 – 127
= [152 + (-73)] + [18 – 127]
= (152 – 73) + [18 + (-127)]
= 79 + [-(127 – 18)]
= 79 + (-109)
= - (109 – 79)
= - 30.
Câu 36:
Thực hiện các phép tính sau: (-99) + (-11)
 Xem đáp án
Xem đáp án
Đáp án C
(-99) + (-11) = - (99 + 11) = -110
Câu 37:
Trong các phát biểu sau, có bao nhiêu phát biểu đúng, bao nhiêu phát biểu nào sai?
a) Tổng của một số nguyên âm và một số nguyên dương là một số nguyên âm.
b) Tổng của một số nguyên dương và một số nguyên âm là một số nguyên dương.
c) Hai số đối nhau có tổng bằng 0.
 Xem đáp án
Xem đáp án
Đáp án A
Phát biểu a) là sai. Vì chẳng hạn ta có -2 là một số nguyên âm và 3 là một số nguyên dương thì tổng (-2) + 3 = 3 – 2 = 1 là một số nguyên dương.
Phát biểu b) là sai. Vì chẳng hạn ta có – 15 là một số nguyên âm và 10 là một số nguyên dường thì tổng (-15) + 10 = - (15 – 10) = -5 là một số nguyên âm.
Phát biểu c) là đúng. Vì tổng của hai số nguyên đối nhau có tổng bằng 0.
Vậy có 2 phát biểu đúng, 1 phát biểu sai.
Câu 38:
Trên trục số, một người bắt đầu từ điểm 0 di chuyển về bên phải (theo chiều dương) 4 đơn vị đến điểm +4. Sau đó, người đó đổi hướng di chuyển về bên trái 4 đơn vị. Hãy cho biết người đó dừng lại tại điểm nào?

 Xem đáp án
Xem đáp án
Đáp án C
Ta có: (+4) + (-4) = 0.
Người đó dừng lại tại điểm 0.
Câu 39:
Trong giờ học nhóm, ba bạn An, Bình, Chi đã lần lượt phát biểu như sau:
a) Bạn An: “Tổng của hai số nguyên dương luôn là một số nguyên dương”.
b) Bạn Bình: “Tổng của hai số nguyên âm luôn là một số nguyên âm”.
c) Bạn Chi: “Tổng của hai số nguyên cùng dấu luôn cùng dấu với hai số nguyên đó”.
Bạn nào phát biểu đúng, bạn nào phát biểu sai?
 Xem đáp án
Xem đáp án
Đáp án D
a) Bạn An phát biểu đúng vì nếu a và b là hai số nguyên dương thì a > 0, b > 0 nên tổng a + b > 0
b) Bạn Bình phát biểu đúng vì nếu a và b là hai số nguyên âm thì a < 0, b < 0 nên tổng a + b < 0
c) Bạn Chi phát biểu đúng vì nếu a và b cùng là hai số nguyên dương thì tổng a + b cũng là số nguyên dương, nếu a và b cùng là hai số nguyên âm thì tổng a + b cũng là số nguyên âm.
Vậy cả ba bạn đều đúng.
Câu 40:
Phát biểu nào sau đây đúng về kết quả của phép tính: (-35) – (-60)
 Xem đáp án
Xem đáp án
Đáp án A
Ta có: (-35) – (-60) = (-35) + 60 = 25;
Kết quả phép tính là một số nguyên dương.
Câu 41:
So sánh kết quả hai biểu thức sau: A = – (12 – 25) và B = (-12 + 25);
 Xem đáp án
Xem đáp án
Đáp án C
Ta có:
A = – (12 – 25) = - [12 + (-25)] = - (-13) =13;
B = (-12 + 25) = 25 – 12 = 13;
Suy ra – (12 – 25) = ( -12 + 25).
Vậy A = B.
Câu 42:
Tính T = - 9 + (-2) – (-3) + (-8).
 Xem đáp án
Xem đáp án
Đáp án D
T = - 9 + (-2) – (-3) + (-8)
= [-9 – (-3)] + [(-2) + (-8)]
= [ - 9 + 3] + (- 10)
= -6 + (-10)
= -16.
Câu 43:
Em hãy dùng số nguyên âm để giải bài toán sau:
Một chiếc tàu ngầm đang ở độ sâu 20 m, tàu tiếp tục lặn thêm 15 m. Hỏi khi đó tàu ngầm ở độ sâu là bao nhiêu mét?
 Xem đáp án
Xem đáp án
Đáp án B
Tàu ngầm đang ở độ sâu 20 m hay tàu đang ở độ cao: - 20 m;
Tàu lặn thêm 15 m nữa được biểu diễn bởi: - 15m;
Khi đó tàu ngầm ở : (- 20) + (-15) = - 35 (m)
Do đó tàu ngầm ở độ cao - 35 m hay tàu ở độ sâu 35 m.
Vậy độ sâu của tàu ngầm ở độ sâu 35 m.
Câu 44:
Thẻ tín dụng trả sau của bác Tám đang ghi nợ 2 000 000 đồng, sau khi bác Tám nộp vào 2 000 000 đồng thì bác Tám có bao nhiêu tiền trong tài khoản? Hãy dùng số nguyên để giải thích.
 Xem đáp án
Xem đáp án
Đáp án C
Thẻ tín dụng đang ghi nợ 2 000 000 đồng được biểu diễn là: - 2 000 000 (đồng).
Bác Tám nộp vào tài khoản 2 000 000 đồng được biểu diễn là: + 2 000 000 (đồng).
Số tiền bác Tám có trong tài khoản là: (+ 2 000 000) + (-2 000 000) = 0 (đồng).
Câu 45:
Tính nhanh các tổng sau: S = (45 – 3 756) + 3 756;
 Xem đáp án
Xem đáp án
Đáp án A
S = (45 – 3 756) + 3 756
= 45 – 3 756 + 3 756
= 45 + [(– 3 756) + 3 756]
= 45 + 0 = 45
Câu 46:
Mũi khoan một giàn khoan trên biển đang ở độ cao 5m so với mực nước biển, chú công nhân điều khiển nó hạ xuống 10m. Vậy mũi khoan ở độ cao nào (so với mực nước biển) sau khi hạ?
 Xem đáp án
Xem đáp án
Đáp án D
Mũi khoan đang ở độ cao: 5 – 10 = -5 (m) so với mực nước biển.
Câu 47:
Thực hiện các phép tính sau: 4 + (-7) + (-5) + 12;
 Xem đáp án
Xem đáp án
Đáp án B
4 + (-7) + (-5) + 12
= 4 + [(-7) + (-5)] + 12
= 4 + (-12) + 12
= 4 + [(-12) + 12]
= 4 + 0
= 4
Câu 48:
Một tòa nhà có tám tầng được đánh số theo thứ tự 0 (tầng mặt đất), 1, 2, 3, ..., 7 và ba tầng hầm được đánh số -1; -2; -3. Em hãy dùng phép cộng các số nguyên để diễn tả hai tình huống sau đây:
Một thang máy đang ở tầng – 3, nó đi lên 5 tầng. Hỏi thang máy dừng lại ở tầng mấy?
(Ở một số tòa nhà, tầng mặt đất còn được gọi là tầng G).
 Xem đáp án
Xem đáp án
Đáp án C
Ta có (-3) + 5 = 5 – 3 = 2.
Thang máy dừng ở tầng 2.
Câu 49:
Bỏ dấu ngoặc rồi tính: (77 + 22 – 65) - (67 + 12 - 75);
 Xem đáp án
Xem đáp án
Đáp án C
(77 + 22 – 65) - (67 + 12 - 75)
= 77 + 22 – 65 – 67 – 12 + 75
= (77 – 67) + (22 – 12) + ( - 65 + 75)
= 10 + 10 + 10
= 30.
Câu 50:
Trong các biểu thức dưới đây, giá trị của biểu thức nào là lớn nhất
M = [(-3) + 4] + 2;
N = (-3) + (4 + 2);
P = [(-3) + 2] + 4.
 Xem đáp án
Xem đáp án
Đáp án D
Ta có:
M = [(-3) + 4] + 2 = (4 – 3) + 2 = 1 + 2 = 3;
N = (-3) + (4 + 2) = (-3) + 6 = 6 – 3 = 3;
P = [(-3) + 2] + 4 = - (3 – 2) + 4 = (-1) + 4 = 4 – 1 = 3.
Suy ra [(-3) + 4] + 2 = (-3) + (4 + 2) = [(-3) + 2] + 4 = 3.
Vậy M = N = P.
Câu 51:
Bác Hà là khách quen của cửa hàng tạp hóa nhà bác Lan nên có thể mua hàng trước, trả tiền sau. Hôm qua bác Lan đã cho bác Hà nợ 80 nghìn đồng, hôm nay bác Hà lại được bác Lan cho nợ thêm 40 nghìn đồng nữa. Em hãy dùng số nguyên để giúp bác Lan ghi vào sổ số tiền bác Hà còn nợ bác Lan.
 Xem đáp án
Xem đáp án
Đáp án B
Bác Hà nợ bác Lan 80 nghìn đồng được biểu diễn là: - 80 000(đồng).
Bác Hà nợ tiếp bác Lan 40 nghìn đồng được biểu diễn là: - 40 000(đồng).
Tổng số tiền bác Hà nợ bác Lan là: (-80) + (-40) = - (80 + 40) = -120 000(đồng).
Câu 52:
Một toà nhà có 12 tầng và 3 tầng hầm (tầng G được đánh số là tầng 0), hãy dùng phép cộng các số nguyên để diễn tả tình huống sau đây: Một thang máy đang ở tầng 3, nó đi lên 7 tầng và sau đó đi xuống 12 tầng. Hỏi cuối cùng thang máy dừng lại tại tầng mấy?

 Xem đáp án
Xem đáp án
Đáp án B
Thang máy đang ở tầng 3 đi lên 7 tầng và sau đó đi xuống 12 tầng sẽ đến: 3 + 7 – 12 = 10 – 12 = -2.
Nghĩa là lúc này thang máy đang ở tầng hầm thứ hai.
Câu 53:
Archimedes (Ác-si-mét) là nhà bác học người Hi Lạp, ông sinh năm 287 TCN và mất năm 212 TCN. Em hãy cho biết Archimedes mất năm bao nhiêu tuổi?

 Xem đáp án
Xem đáp án
Đáp án A
Archimedes sinh năm 287 TCN hay năm sinh của Archimedes là năm - 287
Ông mất năm 212 TCN hay năm mất của Archimedes: - 212
Ta tính tuổi của Archimedes bằng cách lấy năm mất trừ đi năm sinh.
Tuổi của nhà bác học là: (-212) – (-287) = (-212) + 287 = 75 (tuổi)
Vậy Archimedes mất năm 75 tuổi.
Câu 54:
Cho a là số nguyên dương nhỏ nhất có hai chữ số chia hết cho 2 và 5; b là số nguyên âm lớn nhất có ba chữ số. Tính tổng a + b.
 Xem đáp án
Xem đáp án
Đáp án C
Vì a chia hết cho 2 và 5 nên a có chữ số tận cùng là 0.
Hơn nữa a là số nguyên dương nhỏ nhất có hai chữ số nen a = 10.
Ta có b là số nguyên âm lớn nhất có ba chữ số nên b = -100.
Tổng a + b = 10 + (-100) = -(100 – 10) = -90.
Vậy a + b = -90.
Câu 55:
Thực hiện phép tính: (-2) + (-4) + (-6) + (-8) + (-10) + 8 + 10 + 12;
 Xem đáp án
Xem đáp án
Đáp án C
(-2) + (-4) + (-6) + (-8) + (-10) + 8 + 10 + 12
= (-6) + (-6) + [(-8) + 8] + [(-10) + 10] + 12
= (-12) + 0 + 0 + 12
= (-12) + 12
= 12 – 12
= 0
Câu 56:
Cho 43 số nguyên, trong đó tổng của 7 số bất kì là một số nguyên âm. Nhận xét nào sau đây đúng về tổng của 43 số đó.
 Xem đáp án
Xem đáp án
Đáp án A
Trong 43 số nguyên ta có tổng của 7 số nguyên bất kì là một số nguyên âm nên trong đó có ít nhất một số nguyên âm. Gọi số nguyên âm này là a (a < 0). Còn lại 42 số nguyên nghĩa là có 6 tổng của 7 số nguyên âm bất kì mà tổng 7 số nguyên bất kì là một số nguyên âm nên 6 tổng này cũng là một số nguyên âm.
Vì vậy tổng của 43 số đó là số nguyên âm.
Câu 57:
Tính tổng sau: (-1) + (-2) + 3 + 4 + … + (-97) + (-98) + 99 + 100.
 Xem đáp án
Xem đáp án
Đáp án B
(-1) + (-2) + 3 + 4 + … + (-97) + (-98) + 99 + 100
= [(-1) + 3 + (-5) + … + (-97) + 99] + [(-2) + 4 + (-6) + … + (-98) + 100]
Xét (-1) + 3 + (-5) + … + (-97) + 99
Số số hạng của tổng là: [99 – (-1)]:2 + 1 = 50.
Khi đó: (-1) + 3 + (-5) + … + (-97) + 99
= [(-1) + 3] + [(-5) + 7] + … + [(-97) + 99]
= 2 + 2 + … + 2
= 2.(50:2) = 2.25 = 50.
Xét (-2) + 4 + (-6) + … + (-98) + 100
Số số hạng của tổng là: (100 – 2):2 + 1 = 50.
Khi đó: (-2) + 4 + (-6) + … + (-98) + 100
= [(-2) + 4] + [(-6) + 8] + … + [(-98) + 100]
= 2 + 2 + … + 2
= 2.(50:2) = 2.25 = 50.
Suy ra: (-1) + (-2) + 3 + 4 + … + (-97) + (-98) + 99 + 100
= [(-1) + 3 + (-5) + … + (-97) + 99] + [(-2) + 4 + (-6) + … + (-98) + 100]
= 50 + 50 = 100.
