Bài tập cuối Chương 5 trang 110
-
480 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
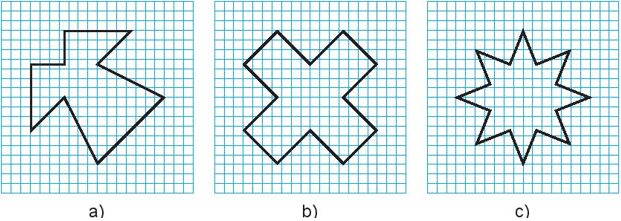
Em hãy vẽ các hình dưới đây vào giấy kẻ ô vuông rồi chỉ ra tất cả các trục đối xứng của chúng (nếu có)
 Xem đáp án
Xem đáp án
+) Hình a) có 1 trục đối xứng.
+) Hình b) có 4 trục đối xứng
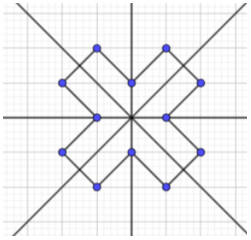
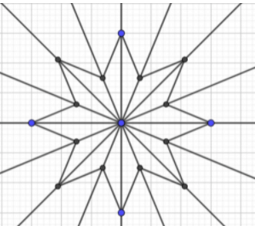
+) Hình c) có 8 trục đối xứng
Câu 3:
Vẽ các hình sau vào vở và vẽ thêm họa tiết để được hình mặt cười nhận đường thẳng d cho trước là trục đối xứng
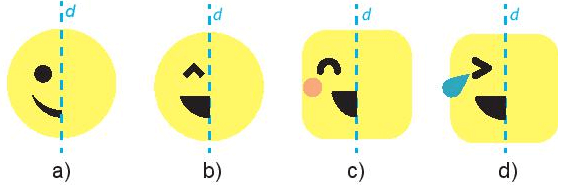
 Xem đáp án
Xem đáp án
Vẽ thêm họa tiết để được hình mặt cười nhận đường thẳng d cho trước là trục đối xứng là:
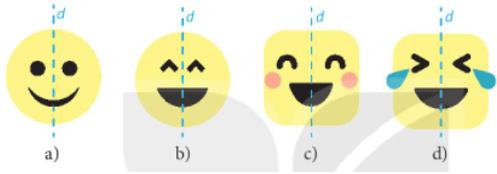
Câu 4:
Vẽ chiếc lá
Vẽ hình bên vào giấy kẻ ô vuông rồi vẽ thêm và trang trí để được hình nhận đường thẳng d là trục đối xứng.
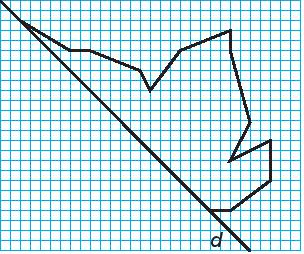
 Xem đáp án
Xem đáp án
Vẽ thêm và trang trí để được hình chiếc lá nhận đường thẳng d là trục đối xứng.
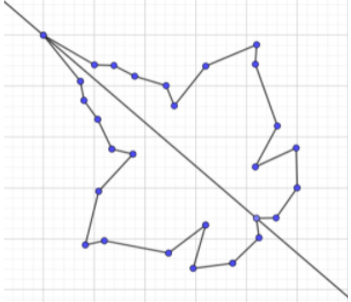
Câu 5:
Trong các hình bên, em hãy chỉ ra:

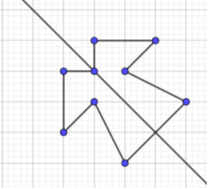
a) Những hình có tâm đối xứng;
b) Những hình có trục đối xứng.
 Xem đáp án
Xem đáp án
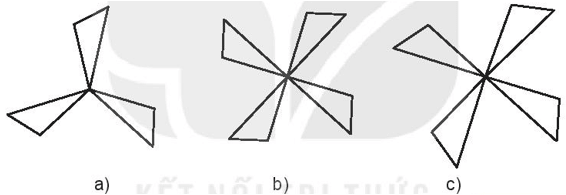
a) Những hình có tâm đối xứng là: cánh quạt.
b) Những hình có trục đối xứng là: tam giác đều, trái tim và cánh diều.
Câu 6:
Nối cột A với cột B để được một phát biểu đúng.
Cột A |
| Cột B |
Hình vuông |
| không có trục đối xứng, cũng không có tâm đối xứng. |
Hình tròn | không có trục đối xứng nhưng có tâm đối xứng. | |
Hình thoi | có vố số trục đối xứng. | |
Hình thang | có bốn trục đối xứng. | |
Hình bình hành | có hai trục đối xứng. |
 Xem đáp án
Xem đáp án
Hình vuông là hình có 4 trục đối xứng là hai đường chéo và hai đường nối trung điểm của các cặp cạnh đối diện.
Hình tròn là hình có vô số trục đối xứng là các đường thẳng đi qua tâm.
Hình thoi là hình có hai trục đối xứng là hai đường chéo.
Hình thang không có trục đối xứng và cũng có tâm đối xứng.
Hình bình hành là hình không có trục đối xứng và có tâm đối xứng.
Ta hoàn thành bảng ghép cột như sau:
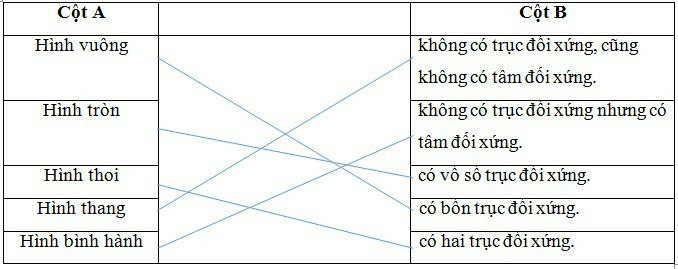
Câu 7:
Trong các câu sau, câu nào đúng?
 Xem đáp án
Xem đáp án
Đáp án D
- Tam giác đều có 3 trục đối xứng nên A sai.
- Hình chữ nhật với hai kích thước có 2 trục đối xứng nên B sai.
- Hình thang cân, góc ở đáy khác 900, có đúng 1 trục đối xứng nên C đúng.
- Hình bình hành không có trục đối xứng nên D sai.
Câu 8:
Trong các câu sau, câu nào sai?
 Xem đáp án
Xem đáp án
Đáp án C
Hình lục giác đều có tất cả 6 trục đối xứng
Do đó C sai.
Câu 9:
Trong các phát biểu sau, có bao nhiêu phát biểu đúng?
a) Số trục đối xứng của tam giác đều nhỏ hơn số trục đối xứng của hình thoi.
b) Hình tròn có một trục đối xứng là đường thẳng đi qua tâm của hình tròn.
c) Hình thang cân có tâm đối xứng là giao điểm của hai đường chéo.
d) Hình chữ nhật có hai trục đối xứng là hai đường chéo.
 Xem đáp án
Xem đáp án
Đáp án A
Tam giác đều có 3 trục đối xứng, hình thoi có 2 trục đối xứng nên a) sai.
Hình tròn có vô số trục đối xứng là các đường thẳng đi qua tâm nên b) sai.
Hình thang cân không có tâm đối xứng nên c) sai.
Hình chữ nhật có hai trục đối xứng là hai đường thẳng nối trung điểm của hai cạnh đối diện nên d) sai.
Vậy không có phát biểu nào đúng.
Câu 10:
Trong các câu sau, câu nào sai?
 Xem đáp án
Xem đáp án
Đáp án A
Hình lục giác đều chỉ có 1 tâm đối xứng là giao điểm của ba đường chéo. Do đó A sai.
Câu 11:
Đoạn thẳng AB có độ dài 4cm. Gọi O là tâm đối xứng của đoạn thẳng AB. Tính độ dài đoạn OA.
 Xem đáp án
Xem đáp án
Đáp án C
Do O là tâm đối xứng của AB nên O chia đoạn thẳng AB thành hai đoạn OA bằng OB và bằng một nửa AB bằng 2cm.
Câu 12:
Cho hình bình hành ABCD có tâm O là tâm đối xứng. Biết OA = 5cm, OD = 7cm, tính độ dài hai đường chéo AC và BD
 Xem đáp án
Xem đáp án
Đáp án D
Do O là tâm đối xứng nên O là giao điểm của hai đường chéo và thỏa mãn OA bằng OC, OB bằng OD.
Suy ra độ dài AC gấp đôi độ dài OA bằng 5.2 = 10cm,
Độ dài BD gấp đôi độ dài OD bằng 7.2 = 14cm.
Vậy AC = 10cm, BD = 14cm.
Câu 13:
Hình thoi ABCD có tâm đối xứng O. Biết OA = 3cm, OB = 2cm. Hãy tính diện tích hình thoi.
 Xem đáp án
Xem đáp án
Đáp án B
Vì O là tâm đối xứng nên độ dài AC gấp đôi độ dài OA bằng 6cm và độ dài BD gấp đôi độ dài OB bằng 4cm.
Diện tích hình thoi ABCD là: 6.4:2= 12 .
Câu 14:
Một chiếc bàn có mặt bàn là hình lục giác đều như hình dưới đây. Biết rằng độ dài đường chéo chính là 1,2m, em hãy tích khoảng cách từ tâm đối xứng của mặt bàn đến mỗi đỉnh và chu vi mặt bàn.
 Xem đáp án
Xem đáp án
Đáp án C
Khoảng cách từ tâm đối xứng đến mỗi đỉnh bằng một nửa đường chéo chính và bằng: 1,2:2 = 0,6 (m).
Do hình lục giác đều được ghép từ 6 tam giác đều nên cạnh của hình lục giác cũng bằng 0,6 (m).
Chu vi mặt bàn là: 0,6.6 = 3.6 (m).
Câu 15:
Một hình tròn có bán kính 6cm, khoảng cách từ tâm đối xứng đến các điểm nằm trên đường tròn bằng:
 Xem đáp án
Xem đáp án
Đáp án C
Tâm đối xứng của hình tròn chính là tâm của đường tròn nên khoảng cách từ tâm đối xứng đến các điểm trên đường tròn đúng bằng bán kính và bằng 6cm.