Trắc nghiệm Các dạng toán về phép cộng và phép trừ phân số (có đáp án)
-
398 lượt thi
-
23 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
\[\frac{{65}}{{91}} + \frac{{ - 44}}{{55}} = \frac{5}{7} + \frac{{ - 4}}{5} = \frac{{25}}{{35}} + \frac{{ - 28}}{{35}} = \frac{{ - 3}}{{35}}\]
Đáp án cần chọn là: C
Câu 2:
 Xem đáp án
Xem đáp án
Đáp án A: \[\frac{{ - 4}}{{11}} + \frac{7}{{ - 11}} = \frac{{ - 4}}{{11}} + \frac{{ - 7}}{{11}} = \frac{{ - 11}}{{11}} = - 1 < 1\] nên A sai
Đáp án B: \[\frac{{ - 4}}{{11}} + \frac{7}{{ - 11}} = \frac{{ - 4}}{{11}} + \frac{{ - 7}}{{11}} = \frac{{ - 11}}{{11}} = - 1 < 0\] nên B đúng.
Đáp án C: \[\frac{8}{{11}} + \frac{7}{{ - 11}} = \frac{8}{{11}} + \frac{{ - 7}}{{11}} = \frac{1}{{11}} < 1\] nên C sai.
Đáp án D: \[\frac{{ - 4}}{{11}} + \frac{{ - 7}}{{11}} = \frac{{ - 11}}{{11}} = - 1\] nên D sai.
Đáp án cần chọn là: B
Câu 3:
 Xem đáp án
Xem đáp án
\[\frac{3}{{13}} + \frac{9}{{20}} = \frac{{60}}{{260}} + \frac{{117}}{{260}} = \frac{{177}}{{260}}\]
Vậy\[x = \frac{{177}}{{260}}\]
Đáp án cần chọn là: B
Câu 4:
 Xem đáp án
Xem đáp án
\[\frac{{ - 9}}{7} + \frac{{13}}{4} + \frac{{ - 1}}{5} + \frac{{ - 5}}{7} + \frac{3}{4}\]
\[ = \left( {\frac{{ - 9}}{7} + \frac{{ - 5}}{7}} \right) + \left( {\frac{{13}}{4} + \frac{3}{4}} \right) + \frac{{ - 1}}{5}\]
\[ = \frac{{ - 14}}{7} + \frac{{16}}{4} + \frac{{ - 1}}{5}\]
\[ = \left( { - 2} \right) + 4 + \frac{{ - 1}}{5}\]
\[ = 2 + \frac{{ - 1}}{5}\]
\[ = \frac{{10}}{5} + \frac{{ - 1}}{5}\]
\[ = \frac{9}{5}\]
Đáp án cần chọn là: A
Câu 5:
 Xem đáp án
Xem đáp án
\[A = \left( {\frac{1}{4} + \frac{{ - 5}}{{13}}} \right) + \left( {\frac{2}{{11}} + \frac{{ - 8}}{{13}} + \frac{3}{4}} \right)\]
\[A = \frac{1}{4} + \frac{{ - 5}}{{13}} + \frac{2}{{11}} + \frac{{ - 8}}{{13}} + \frac{3}{4}\]
\[A = \left( {\frac{1}{4} + \frac{3}{4}} \right) + \left( {\frac{{ - 5}}{{13}} + \frac{{ - 8}}{{13}}} \right) + \frac{2}{{11}}\]
\[A = 1 + \left( { - 1} \right) + \frac{2}{{11}}\]
\[A = \frac{2}{{11}}\]
Đáp án cần chọn là: B
Câu 6:
Chọn câu đúng.
 Xem đáp án
Xem đáp án
\[M = \left( {\frac{{21}}{{31}} + \frac{{ - 16}}{7}} \right) + \left( {\frac{{44}}{{53}} + \frac{{10}}{{31}}} \right) + \frac{9}{{53}}\]
\[M = \frac{{21}}{{31}} + \frac{{ - 16}}{7} + \frac{{44}}{{53}} + \frac{{10}}{{31}} + \frac{9}{{53}}\]
\[M = \left( {\frac{{21}}{{31}} + \frac{{10}}{{31}}} \right) + \left( {\frac{{44}}{{53}} + \frac{9}{{53}}} \right) + \frac{{ - 16}}{7}\]
\[M = 1 + 1 + \frac{{ - 16}}{7}\]
\[M = 2 + \frac{{ - 16}}{7}\]
\[M = \frac{{ - 2}}{7}\]
\[N = \frac{1}{2} + \frac{{ - 1}}{5} + \frac{{ - 5}}{7} + \frac{1}{6} + \frac{{ - 3}}{{35}} + \frac{1}{3} + \frac{1}{{41}}\]
\[N = \left( {\frac{1}{2} + \frac{1}{6} + \frac{1}{3}} \right) + \left( {\frac{{ - 1}}{5} + \frac{{ - 5}}{7} + \frac{{ - 3}}{{35}}} \right) + \frac{1}{{41}}\]
\[N = \frac{{3 + 1 + 2}}{6} + \frac{{\left( { - 7} \right) + \left( { - 25} \right) + \left( { - 3} \right)}}{{35}} + \frac{1}{{41}}\]
\[\begin{array}{l}N = 1 + \left( { - 1} \right) + \frac{1}{{41}}\\N = \frac{1}{{41}}\end{array}\]
Đáp án cần chọn là: D
Câu 7:
 Xem đáp án
Xem đáp án
\[\frac{5}{6} + \frac{{ - 7}}{8} \le \frac{x}{{24}} \le \frac{{ - 5}}{{12}} + \frac{5}{8}\]
\[\begin{array}{l}\frac{{ - 1}}{{24}} \le \frac{x}{{24}} \le \frac{5}{{24}}\\ - 1 \le x \le 5\end{array}\]
\[x \in \left\{ { - 1;0;1;2;3;4;5} \right\}\]
Đáp án cần chọn là: B
Câu 8:
 Xem đáp án
Xem đáp án
Ta có:
\[\begin{array}{l}\frac{{n - 8}}{{n + 1}} + \frac{{n + 3}}{{n + 1}} = \frac{{n - 8 + n + 3}}{{n + 1}} = \frac{{2n - 5}}{{n + 1}} = \frac{{\left( {2n + 2} \right) - 7}}{{n + 1}} = \frac{{2\left( {n + 1} \right) - 7}}{{n + 1}}\\ = \frac{{2\left( {n + 1} \right)}}{{n + 1}} - \frac{7}{{n + 1}} = 2 - \frac{7}{{n + 1}}\end{array}\]
Yêu cầu bài toán thỏa mãn nếu \[\frac{7}{{n + 1}} \in Z\] hay n + 1 ∈ Ư(7) = {±1; ±7}
Ta có bảng:
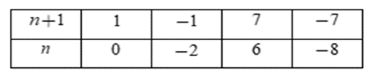
Vậy n ∈ {0; −2; 6; −8}
Đáp án cần chọn là: C
Câu 9:
 Xem đáp án
Xem đáp án
\[\frac{{15}}{{41}} + \frac{{ - 138}}{{41}} \le x < \frac{1}{2} + \frac{1}{3} + \frac{1}{6}\]
−3 ≤ x < 1
x ∈ {− 3; −2; −1;0}
Vậy có tất cả 4 giá trị của x
Đáp án cần chọn là: D
Câu 10:
 Xem đáp án
Xem đáp án
\[A = \frac{1}{2} + \frac{1}{6} + \frac{1}{{12}} + \ldots + \frac{1}{{99.100}}\]
\[A = \frac{1}{{1.2}} + \frac{1}{{2.3}} + \frac{1}{{3.4}} + ... + \frac{1}{{99.100}}\]
\[A = 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + ... + \frac{1}{{99}} - \frac{1}{{100}}\]
\[A = 1 - \frac{1}{{100}} = \frac{{99}}{{100}}\]
So sánh A với \[\frac{3}{5}\] và \[\frac{4}{5}\]
Ta có: \[\frac{3}{5} = \frac{{60}}{{100}};\frac{4}{5} = \frac{{80}}{{100}}\]
\[ \Rightarrow \frac{{60}}{{100}} < \frac{{80}}{{100}} < \frac{{99}}{{100}} \Rightarrow A >\frac{4}{5} >\frac{3}{5}\]Đáp án cần chọn là: D
Câu 11:
 Xem đáp án
Xem đáp án
\[S = \frac{1}{{21}} + \frac{1}{{22}} + \frac{1}{{23}} + ... + \frac{1}{{35}}\]
\[S = \left( {\frac{1}{{21}} + ... + \frac{1}{{25}}} \right) + \left( {\frac{1}{{26}} + ... + \frac{1}{{30}}} \right) + \left( {\frac{1}{{31}} + ... + \frac{1}{{35}}} \right)\]
\[S >\left( {\frac{1}{{25}} + ... + \frac{1}{{25}}} \right) + \left( {\frac{1}{{30}} + ... + \frac{1}{{30}}} \right) + \left( {\frac{1}{{35}} + ... + \frac{1}{{35}}} \right)\]
\[S >\frac{1}{5} + \frac{1}{6} + \frac{1}{7} = \frac{{107}}{{210}} >\frac{1}{2}\]
Vậy \[S >\frac{1}{2}\]
Đáp án cần chọn là: A
Câu 12:
 Xem đáp án
Xem đáp án
\[\frac{a}{5} + \frac{1}{{10}} = \frac{{ - 1}}{b}\]
\[\frac{{2{\rm{a}}}}{{10}} + \frac{1}{{10}} = \frac{{ - 1}}{b}\]
\[\frac{{2{\rm{a}} + 1}}{{10}} = \frac{{ - 1}}{b}\]
\[\left( {2{\rm{a}} + 1} \right).b = - 10\]
2a + 1 là số lẻ; 2a + 1 là ước của −10
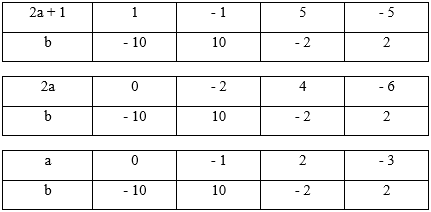
Vậy có 44 cặp số (a;b)(a;b) thỏa mãn bài toán.
Đáp án cần chọn là: C
Câu 13:
 Xem đáp án
Xem đáp án
\[\frac{3}{4} - \frac{7}{{20}} = \frac{{15}}{{20}} - \frac{7}{{20}} = \frac{8}{{20}} = \frac{2}{5}\]
Đáp án cần chọn là: C
Câu 14:
 Xem đáp án
Xem đáp án
\[\frac{{15}}{{20}} - x = \frac{7}{{16}}\]
\[\begin{array}{*{20}{l}}{ - x = \frac{7}{{16}} - \frac{{15}}{{20}}}\\{ - x = - \frac{5}{{16}}}\\{x = \frac{5}{{16}}}\end{array}\]
Đáp án cần chọn là: B
Câu 15:
 Xem đáp án
Xem đáp án
\[\frac{4}{{15}} - \frac{2}{{65}} - \frac{4}{{39}}\]
\[ = \frac{{52}}{{195}} - \frac{6}{{195}} - \frac{{20}}{{195}}\]
\[ = \frac{{52 - 6 - 20}}{{195}}\]
\[ = \frac{{26}}{{195}} = \frac{2}{{15}}\]
Đáp án cần chọn là: B
Câu 16:
 Xem đáp án
Xem đáp án
\[\begin{array}{*{20}{l}}{B = \frac{{31}}{{23}} - \left( {\frac{7}{{30}} + \frac{8}{{23}}} \right)}\\{B = \frac{{31}}{{23}} - \frac{7}{{30}} - \frac{8}{{23}}}\\{B = \left( {\frac{{31}}{{23}} - \frac{8}{{23}}} \right) - \frac{7}{{30}}}\\{B = 1 - \frac{7}{{30}}}\\{B = \frac{{23}}{{30}}}\end{array}\]
Đáp án cần chọn là: A
Câu 17:
 Xem đáp án
Xem đáp án
\[M = \left( {\frac{1}{3} + \frac{{12}}{{67}} + \frac{{13}}{{41}}} \right) - \left( {\frac{{79}}{{67}} - \frac{{28}}{{41}}} \right)\]
\[M = \frac{1}{3} + \frac{{12}}{{67}} + \frac{{13}}{{41}} - \frac{{79}}{{67}} + \frac{{28}}{{41}}\]
\[M = \frac{1}{3} + \left( {\frac{{12}}{{67}} - \frac{{79}}{{67}}} \right) + \left( {\frac{{13}}{{41}} + \frac{{28}}{{41}}} \right)\]
\[M = \frac{1}{3} + \left( { - 1} \right) + 1\]
\[M = \frac{1}{3}\]
\[\begin{array}{*{20}{l}}{N = \frac{{38}}{{45}} - \left( {\frac{8}{{45}} - \frac{{17}}{{51}} - \frac{3}{{11}}} \right)}\\{N = \frac{{38}}{{45}} - \frac{8}{{45}} + \frac{{17}}{{51}} + \frac{3}{{11}}}\\{N = \left( {\frac{{38}}{{45}} - \frac{8}{{45}}} \right) + \frac{{17}}{{51}} + \frac{3}{{11}}}\\{N = \frac{2}{3} + \frac{1}{3} + \frac{3}{{11}}}\\{N = 1 + \frac{3}{{11}}}\\{N = \frac{{14}}{{11}}}\end{array}\]
Vì \[\frac{1}{3} < 1 < \frac{{14}}{{11}}\] nên M < 1 < N
Đáp án cần chọn là: D
Câu 18:
 Xem đáp án
Xem đáp án
\[\begin{array}{*{20}{l}}{x - \frac{{ - 7}}{{12}} = \frac{{17}}{{18}} - \frac{1}{9}}\\{x - \frac{{ - 7}}{{12}} = \frac{5}{6}}\\{x = \frac{5}{6} + \frac{{ - 7}}{{12}}}\\{x = \frac{1}{4}}\end{array}\]
Đáp án cần chọn là: C
Câu 19:
 Xem đáp án
Xem đáp án
\[\begin{array}{*{20}{l}}{\frac{{29}}{{30}} - \left( {\frac{{13}}{{23}} + x} \right) = \frac{7}{{69}}}\\{\frac{{13}}{{23}} + x = \frac{{29}}{{30}} - \frac{7}{{69}}}\\{\frac{{13}}{{23}} + x = \frac{{199}}{{230}}}\\{x = \frac{{199}}{{230}} - \frac{{13}}{{23}}}\\{x = \frac{3}{{10}}}\end{array}\]
Đáp án cần chọn là: A
Câu 20:
 Xem đáp án
Xem đáp án
\[\frac{{ - 5}}{{14}} - \frac{{37}}{{14}} \le x \le \frac{{31}}{{73}} - \frac{{313131}}{{737373}}\]
\[\frac{{ - 5}}{{14}} + \frac{{ - 37}}{{14}} \le x \le \frac{{31}}{{73}} - \frac{{313131:10101}}{{737373:10101}}\]
\[\frac{{ - 42}}{{14}} \le x \le \frac{{31}}{{73}} - \frac{{31}}{{73}}\]
\[ - 3 \le x \le 0\]
\[x \in \left\{ { - 3; - 2; - 1;0} \right\}\]
Vậy có 4 giá trị của x thỏa mãn bài toán.
Đáp án cần chọn là: C
Câu 21:
Câu 18093
Vận dụngHai vòi nước cùng chảy vào một bể cạn. Vòi thứ nhất chảy riêng trong 10 giờ đầy bể, vòi thứ hai chảy riêng trong 8 giờ đầy bể. Vòi thứ ba tháo nước ra sau 5 giờ thì bể cạn. Nếu bể đang cạn, ta mở cả ba vòi thì sau 1 giờ chảy được bao nhiêu phần bể?
 Xem đáp án
Xem đáp án
Trong 1 giờ, vòi thứ nhất chảy được là: \[1:10 = \frac{1}{{10}}\] (bể)
Trong 1 giờ, vòi thứ hai chảy được là: \[1:8 = \frac{1}{8}\] (bể)
Trong 1 giờ, vòi thứ ba tháo được là: \[1:5 = \frac{1}{5}\] (bể)
Sau 11 giờ, lượng nước trong bể có là:
\[\frac{1}{{10}} + \frac{1}{8} - \frac{1}{5} = \frac{1}{{40}}\] (bể)
Đáp án cần chọn là: B
Câu 22:
 Xem đáp án
Xem đáp án
\[x + \frac{4}{{5.9}} + \frac{4}{{9.13}} + \frac{4}{{13.17}} + ... + \frac{4}{{41.45}} = \frac{{ - 37}}{{45}}\]
\[x + \frac{1}{5} - \frac{1}{9} + \frac{1}{9} - \frac{1}{{13}} + ... + \frac{1}{{41}} - \frac{1}{{45}} = - \frac{{37}}{{45}}\]
\[x + \frac{1}{5} - \frac{1}{{45}} = - \frac{{37}}{{45}}\]
\[x + \frac{8}{{45}} = - \frac{{37}}{{45}}\]
\[x = - \frac{{37}}{{45}} - \frac{8}{{45}}\]
\[x = - 1\]
Vì -1là số nguyên âm nên đáp án A đúng.
Đáp án cần chọn là: A
Câu 23:
 Xem đáp án
Xem đáp án
\[P = \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + ... + \frac{1}{{{{2002}^2}}} + \frac{1}{{{{2003}^2}}}\]
\[ < \frac{1}{{1.2}} + \frac{1}{{2.3}} + ... + \frac{1}{{2001.2002}} + \frac{1}{{2002.2003}}\]
\[ = \frac{1}{1} - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + ... + \frac{1}{{2001}} - \frac{1}{{2002}} + \frac{1}{{2002}} - \frac{1}{{2003}}\]
\[ = 1 - \frac{1}{{2003}} = \frac{{2002}}{{2003}} < 1\]
Vậy P < 1
Đáp án cần chọn là: C
