Trắc nghiệm Bài tập ôn tập chương 1: Số tự nhiên (có đáp án)
-
1318 lượt thi
-
24 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Tập hợp các số tự nhiên khác 0 và nhỏ hơn 5 là:
 Xem đáp án
Xem đáp án
Tập hợp các số tự nhiên khác 0 và nhỏ hơn 5 là tập hợp {1;2;3;4}
Đáp án cần chọn là: C
Câu 2:
Số la mã XVII có giá trị là:
 Xem đáp án
Xem đáp án
Số la mã XVII có giá trị tương ứng trong hệ thập phân là 17.
Đáp án cần chọn là: D
Câu 5:
Chọn câu đúng.
 Xem đáp án
Xem đáp án
Ta có:
10000 = 104
10200 = 1
x.x7 = x1+7 = x8
127:124 = 127-4 = 123
Do đó chỉ có đáp án D đúng.
Đáp án cần chọn là: D
Câu 6:
Tập hợp A = {3, 6, 9, 12,..., 150} có số phần tử là:
 Xem đáp án
Xem đáp án
Số phần tử của tập hợp chính là số số hạng của dãy 3, 6, 9,…, 150 và bằng:
(150 − 3):3 + 1 = 50
Đáp án cần chọn là: C
Câu 7:
Cho tập hợp A = {x∈N|5 < x < 50, x⋮15}. Các phần tử của A là:
 Xem đáp án
Xem đáp án
Theo đề bài thì ta tìm trong khoảng từ 5 đến 50 các số chia hết cho 15 là: 15, 30, 45.
Do đó A = {15, 30, 45}
Đáp án cần chọn là: A
Câu 8:
Cho tập hợp A = {x∈N|2 < x ≤ 8}. Kết luận nào sau đây không đúng?
 Xem đáp án
Xem đáp án
Trong cách viết A = {x∈N|2 < x ≤ 8}, ta chỉ ra tính chất đặc trưng cho các phần tử x của tập hợp A đó là x >2 và x ≤ 8 . Do đó 2 không là phần tử của tập A nên C sai.
Tập A còn có cách viết: A={3;4;5;6;7;8}⇒A có 6 phần tử nên đáp án B đúng. Dễ thấy A, D đều đúng.
Đáp án cần chọn là: C
Câu 9:
Số phần tử của tập hợp các số tự nhiên chẵn lớn hơn 10 nhưng không vượt quá 2012 là:
 Xem đáp án
Xem đáp án
Gọi B là tập hợp các số tự nhiên chẵn lớn hơn 10 nhưng không vượt quá 2012.
B={1012;1014;1016;...;2008;2012}
Xét dãy số 1012;1014;1016;...;2008;2012
Ta thấy dãy trên là dãy số cách đều 2 đơn vị
Số số hạng của dãy số trên là: (2012−1012):2+1=501 số hạng
Số phần tử của tập hợp B cũng chính là số số hạng của dãy số trên
Nên tập hợp các số tự nhiên chẵn lớn hơn 1010 nhưng không vượt quá 2012 có 501 phần tử.
Đáp án cần chọn là: D
Câu 10:
Cho tập hợp X = {2; 4}; Y = {1; 3; 7}Tập hợp M gồm các phần tử mà mỗi phần tử là tích của một phần tử thuộc X và một phần tử thuộc Y là:
 Xem đáp án
Xem đáp án
X = {2; 4}; Y = {1; 3; 7}
Lấy mỗi phần tử thuộc tập hợp X nhân lần lượt với từng phần tử thuộc tập hợp Y ta được:
2.1 = 2; 2.3 = 6; 2.7 = 14; 4.1 = 4; 4.3 = 12; 4.7 = 28
Vậy M = {2; 6; 14; 4; 12; 28}
Đáp án cần chọn là: A
Câu 11:
 Xem đáp án
Xem đáp án
Ta có:
914 − [(x − 300) + x] = 654
914 − (x – 300 + x) = 654
914 − (2x − 300) = 654
2x – 300 = 914 − 654
2x – 300 = 260
2x = 260 + 300
2x = 560
x = 560:2
x = 280
Vậy x = 280.
Đáp án cần chọn là: B
Câu 12:
BCNN(9; 24) là bao nhiêu?
 Xem đáp án
Xem đáp án
Ta có:
9 = 32; 24 = 23.3
⇒ BCNN(9; 24) = 23.33 = 8.9 = 72
Đáp án cần chọn là: C
Câu 13:
Chọn câu đúng. BCNN(18; 32; 50) là một số:
 Xem đáp án
Xem đáp án
Ta có:
18 = 2.32; 32 = 25; 50 = 2.52
Nên BCNN(18; 32; 50) = 25.32.52 = 7200.
Vì 7200 chia hết cho 10 nên C đúng.
Đáp án cần chọn là: C
Câu 14:
Tìm số tự nhiên a lớn nhất biết: 525⁝a; 875⁝a; 280⁝a
 Xem đáp án
Xem đáp án
Vì 525⁝a; 875⁝a; 280⁝a và a là số lớn nhất
⇒ a = ƯCLN(525; 875; 280) Ta có:
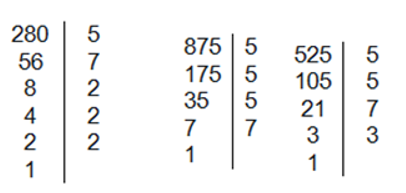
Nên
525 = 3.52.7; 875 = 53.7; 280 = 23.5.7
⇒ a = ƯCLN(525; 875; 280) = 5.7 = 35
Đáp án cần chọn là: D
Câu 15:
Có bao nhiêu số tự nhiên x biết x⋮5; x⋮6 và 0 < x < 100.
 Xem đáp án
Xem đáp án
Do x⋮5;x⋮6 ⇒ x∈BC(5; 6) = {0; 30; 60; 90; 120;...}
Mà 0 < x < 100 nên x∈{30; 60; 90}
Vậy x∈{30; 60; 90}
Đáp án cần chọn là: D
Câu 16:
Cho A = 18 + 36 + 72 + 2x. Tìm giá trị của x biết rằng A chia hết cho 9 và 45 < x < 55
 Xem đáp án
Xem đáp án
Ta có A=18+36+72+2x
mà A⁝9; 18⁝9; 36⁝9; 72⁝9 ⇒ 2x⁝9 ⇒ x⁝9
Mà 45 < x < 55 ⇒ x = 54
Vậy x = 54.
Đáp án cần chọn là: B
Câu 17:
Một trường học có khoảng từ 100 đến 150 học sinh khối 6. Khi xếp thành 10 hàng, 12 hàng, 15 hàng đều vừa đủ. Vậy hỏi số học sinh khối 6 của trường đó là bao nhiêu?
 Xem đáp án
Xem đáp án
Gọi số học sinh khối 6 là x (x∈N*) (học sinh)
Theo bài ra ta có:
x⁝10, x⁝12; x⁝15 ⇒ x∈BC(10; 12; 15) và 100 ≤ x ≤ 150.
Ta có
10 = 2.5; 12 = 22.3;15 = 3.5
⇒ BCNN(10; 12; 15) = 22.3.5 = 60
⇒ BC(10; 12; 15) = {0; 60; 120; 180;...}
⇒ x {0; 60; 120; 180;...}
Mà 100 ≤ x ≤ 150 nên x = 120.
Vậy số học sinh khổi 6 là 120 bạn.
Đáp án cần chọn là: B
Câu 18:
Một buổi liên hoan ban tổ chức đã mua tất cả 840 cái bánh, 2352 cái kẹo và 560 quả quýt chia đều ra các đĩa, mỗi đĩa gồm cả bánh, kẹo và quýt. Tính số đĩa nhiều nhất mà ban tổ chức phải chuẩn bị?
 Xem đáp án
Xem đáp án
Gọi số đĩa cần chẩn bị là x cái (x∈N*)
Vì số bánh, kẹo và quýt được chia đều vào các đĩa nên: 840⁝x; 2352⁝x; 560⁝x
Và x là lớn nhất nên x = ƯCLN(840; 2352; 560)
Ta có:
840 = 23.3.5.7; 560 = 24.5.7; 2352 = 24.3.72
Suy ra ƯCLN(840; 2352; 560) = 23.7 = 56
Vậy số đĩa nhiều nhất cần chuẩn bị là 56 .
Đáp án cần chọn là: D
Câu 19:
Giá trị của A = 28.231 + 69.28 + 72.231 + 69.72 gần nhất với số nào dưới đây?
 Xem đáp án
Xem đáp án
Ta có:
28.231 + 69.28 + 72.231 + 69.72
= (28.231 + 69.28) + (72.231 + 69.72)
= 28.(231 + 69) + 72.(231 + 69)
= 28.300 + 72.300
= 300.(28 + 72)
= 300.100
= 30000
Nhận thấy số 30000 gần với số 30005 nhất trong các đáp án nên chọn A.
Đáp án cần chọn là: A
Câu 20:
Tìm x biết:
(2x − 130):4 + 213 = 52 + 193
 Xem đáp án
Xem đáp án
(2x − 130):4 + 213 = 52 + 193
(2x − 130):4 + 213 = 25 + 193
(2x − 130):4 + 213 = 218
(2x − 130):4 = 218 − 213
(2x − 130):4 = 52
x – 130 = 5.42
x – 130 = 202
x = 20 + 1302
x = 150
x = 150:2
x = 75
Đáp án cần chọn là: D
Câu 21:
Tìm một số có hai chữ số biết rằng khi viết thêm chữ số 0 vào giữa hai chữ số của số đó thì được số mới gấp 7 lần số đã cho.
 Xem đáp án
Xem đáp án
Gọi số có hai chữ số cần tìm là \[\overline {ab} \] (0 < a ≤ 9; 0 ≤ b ≤ 9; a,b∈N).
Khi viết thêm chữ số 0 vào giữa hai chữ số ta được số mới là \[\overline {a0b} \]
Theo bài ra ta có:
\[\overline {a0b} = 7.\overline {ab} \]
100.a + b = 7.(10.a + b)
100.a + b = 70.a + 7.b
100.a − 70.a = 7.b − b
30.a = 6.b
5.a = b
Vì a, b là các chữ số và a ≠ 0 nên a = 1; b = 5
Vậy số cần tìm là 15.
Đáp án cần chọn là: A
Câu 22:
Biết 4 số tự nhiên liên tiếp mà tổng bằng 2010. Số nhỏ nhất trong 4 số đó là
 Xem đáp án
Xem đáp án
Gọi n∈N ta có các số: n; n+1; n+2; n+3 là 4 số tự nhiên liên tiếp.
Theo đề bài ta có:
n + (n + 1) + (n + 2) + (n + 3) = 2010
4.n + 6 = 2010
4n = 2010−6
4n = 2004
n = 2004:4
n = 501.
Vậy 4 số tự nhiên đó là 501; 502; 503; 504.
Số nhỏ nhất là 501.
Đáp án cần chọn là: D
Câu 23:
Cần bao nhiêu chữ số để đánh số trang (bắt đầu từ trang 1) của một cuốn sách có 1031 trang?
 Xem đáp án
Xem đáp án
Ta chia các số trang của cuốn sách thành 4 nhóm:
+ Nhóm các số có 1 chữ số (từ trang 1 đến trang 9): số chữ số cần dùng là 9.
+ Nhóm các số có hai chữ số (từ trang 10 đến trang 99): số trang sách là:
(99 − 10):1 + 1 = 90, số chữ số cần dùng là: 90.2 = 180 .
+ Nhóm các số có 3 chữ số (từ trang 100 đến trang 999): số trang sách là:
(999 − 100):1 + 1 = 900
, số chữ số cần dùng để đánh số trang nhóm này là: 900.3 = 2700.
+Nhóm các số có 4 chữ số (từ trang 1000 đến trang 1031): số trang sách là:
(1031 − 1000):1 + 1 = 32 ; số chữ số cần dùng là 32.4 = 128 .
Vậy tổng số chữ số cần dùng để đánh số trang cuốn sách đó là:
9 + 180 + 2700 + 128 = 3017
Đáp án cần chọn là: C
Câu 24:
Cho 2 số: 14n + 3 và 21n + 4 với n là số tự nhiên, chọn đáp án đúng.
 Xem đáp án
Xem đáp án
Gọi d = UCLN(14n+3; 21n+4) ta có:
\[\left. {\begin{array}{*{20}{c}}{14n + 3 \vdots d}\\{21n + 4 \vdots d}\end{array}} \right\} \Rightarrow \left. {\begin{array}{*{20}{c}}{3\left( {14n + 3} \right) \vdots d}\\{2\left( {21n + 4} \right) \vdots d}\end{array}} \right\} \Rightarrow \left. {\begin{array}{*{20}{c}}{42n + 9 \vdots d}\\{42n + 8 \vdots d}\end{array}} \right\}\]
\[ \Rightarrow \left( {42n + 9} \right) - \left( {42n + 8} \right) \vdots d \Rightarrow 1 \vdots d \Rightarrow d = 1\]
Vậy ƯCLN(14n + 3; 21n + 4) = 1 hay hai số đó là hai số nguyên tố cùng nhau.
Đáp án cần chọn là: C
