Trắc nghiệm Các dạng toán về phép nhân và phép chia phân số (có đáp án)
-
1118 lượt thi
-
25 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 1:
Tính \[\frac{5}{8}\; \cdot \frac{{ - 3}}{4}\]
 Xem đáp án
Xem đáp án
\[\frac{5}{8}\; \cdot \frac{{ - 3}}{4} = \frac{{5.\left( { - 3} \right)}}{{8.4}} = \frac{{ - 15}}{{32}}\]
Đáp án cần chọn là: C
Câu 2:
Chọn câu đúng
 Xem đáp án
Xem đáp án
Đáp án A: \[{\left( {\frac{{ - 7}}{6}} \right)^2} = \frac{{{{\left( { - 7} \right)}^2}}}{{{6^2}}} = \frac{{49}}{{36}} \ne \frac{{ - 49}}{{36}}\] nên A sai.
Đáp án B: \[{\left( {\frac{2}{3}} \right)^3} = \frac{{{2^3}}}{{{3^3}}} = \frac{8}{{27}} \ne \frac{8}{9}\] nên B sai.
Đáp án C: \[{\left( {\frac{2}{{ - 3}}} \right)^3} = \frac{{{2^3}}}{{{{\left( { - 3} \right)}^3}}} = \frac{8}{{ - 27}}\] nên C đúng.
Đáp án D: \[{\left( {\frac{{ - 2}}{3}} \right)^4} = \frac{{{{\left( { - 2} \right)}^4}}}{{{3^4}}} = \frac{{16}}{{81}} \ne \frac{{ - 16}}{{81}}\] nên D sai.
Đáp án cần chọn là: C
Câu 3:
Tìm số nguyên x biết \[\frac{{ - 5}}{6}.\frac{{120}}{{25}} < x < \frac{{ - 7}}{{15}}.\frac{9}{{14}}\]
 Xem đáp án
Xem đáp án
\[\frac{{ - 5}}{6}.\frac{{120}}{{25}} < x < \frac{{ - 7}}{{15}}.\frac{9}{{14}}\]
\[\frac{{ - 5}}{6}.\frac{{24}}{5} < x < \frac{{ - 1}}{5}.\frac{3}{2}\]
\[ - 4 < x < \frac{{ - 3}}{{10}}\]
\[x \in \{ - 3; - 2; - 1\} \]
Đáp án cần chọn là: A
Câu 4:
Có bao nhiêu giá trị nguyên dương của x thỏa mãn \[{\left( {\frac{{ - 5}}{3}} \right)^3} < x < \frac{{ - 24}}{{35}}.\frac{{ - 5}}{6}\] ?
 Xem đáp án
Xem đáp án
Vì x nguyên dương nên x >0
mà \[{\left( {\frac{{ - 5}}{3}} \right)^3} = \frac{{ - 125}}{{27}} < 0\] nên \[{\left( {\frac{{ - 5}}{3}} \right)^3} < 0 < x < \frac{{ - 24}}{{35}}.\frac{{ - 5}}{6}\]
Khi đó: \[0 < x < \frac{{ - 24}}{{35}}.\frac{{ - 5}}{6}\]
\[0 < x < \frac{4}{7}\]
Vì \[\frac{4}{7} < 1\] nên 0 < x < 1 nên không có số nguyên dương nào thỏa mãn.
Đáp án cần chọn là: B
Câu 5:
Có bao nhiêu giá trị của x thỏa mãn \[\left( {\frac{7}{6} + x} \right):\frac{{16}}{{25}} = \frac{{ - 5}}{4}\] ?
 Xem đáp án
Xem đáp án
\[\left( {\frac{7}{6} + x} \right):\frac{{16}}{{25}} = \frac{{ - 5}}{4}\]
\[\frac{7}{6} + x = \frac{{ - 5}}{4}.\frac{{16}}{{25}}\]
\[\frac{7}{6} + x = \frac{{ - 1}}{1}.\frac{4}{5}\]
\[\frac{7}{6} + x = \frac{{ - 4}}{5}\]
\[\begin{array}{l}x = \frac{{ - 4}}{5} - \frac{7}{6}\\x = \frac{{ - 59}}{{30}}\end{array}\]
Đáp án cần chọn là: C
Câu 6:
Cho \[M = \frac{{17}}{5}.\frac{{ - 31}}{{125}}.\frac{1}{2}.\frac{{10}}{{17}}.{\left( {\frac{{ - 1}}{2}} \right)^3}\] và \[N = \left( {\frac{{17}}{{28}} + \frac{{28}}{{29}} - \frac{{19}}{{30}} - \frac{{20}}{{31}}} \right).\left( {\frac{{ - 5}}{{12}} + \frac{1}{4} + \frac{1}{6}} \right)\] . Khi đó tổng M + N bằng
 Xem đáp án
Xem đáp án
\[M = \frac{{17}}{5}.\frac{{ - 31}}{{125}}.\frac{1}{2}.\frac{{10}}{{17}}.{\left( {\frac{{ - 1}}{2}} \right)^3}\]
\[M = \frac{{17.\left( { - 31} \right).1.10.{{\left( { - 1} \right)}^3}}}{{{{5.125.2.17.2}^3}}}\]
\[M = \frac{{ - 31.\left( { - 1} \right)}}{{{{125.2}^3}}}\]
\[M = \frac{{31}}{{1000}}\]
\[N = \left( {\frac{{17}}{{28}} + \frac{{28}}{{29}} - \frac{{19}}{{30}} - \frac{{20}}{{31}}} \right).\left( {\frac{{ - 5}}{{12}} + \frac{1}{4} + \frac{1}{6}} \right)\]
\[N = \left( {\frac{{17}}{{28}} + \frac{{28}}{{29}} - \frac{{19}}{{30}} - \frac{{20}}{{31}}} \right).\left( {\frac{{ - 5}}{{12}} + \frac{3}{{12}} + \frac{2}{{12}}} \right)\]
\[N = \left( {\frac{{17}}{{28}} + \frac{{28}}{{29}} - \frac{{19}}{{30}} - \frac{{20}}{{31}}} \right).0\]
N = 0
Vậy \[M + N = \frac{{31}}{{1000}} + 0 = \frac{{31}}{{1000}}\]
Đáp án cần chọn là: B
Câu 7:
Tính \[B = \frac{{{2^2}}}{3} \cdot \frac{{{3^2}}}{8} \cdot \frac{{{4^2}}}{{15}} \cdot \frac{{{5^2}}}{{24}} \cdot \frac{{{6^2}}}{{35}} \cdot \frac{{{7^2}}}{{48}} \cdot \frac{{{8^2}}}{{63}} \cdot \frac{{{9^2}}}{{80}}\] ta được
 Xem đáp án
Xem đáp án
\[B = \frac{{{2^2}}}{3} \cdot \frac{{{3^2}}}{8} \cdot \frac{{{4^2}}}{{15}} \cdot \frac{{{5^2}}}{{24}} \cdot \frac{{{6^2}}}{{35}} \cdot \frac{{{7^2}}}{{48}} \cdot \frac{{{8^2}}}{{63}} \cdot \frac{{{9^2}}}{{80}}\]
\[ = \frac{{2.2}}{{1.3}} \cdot \frac{{3.3}}{{2.4}} \cdot \frac{{4.4}}{{3.5}} \cdot \frac{{5.5}}{{4.6}} \cdot \frac{{6.6}}{{5.7}} \cdot \frac{{7.7}}{{6.8}} \cdot \frac{{8.8}}{{7.9}} \cdot \frac{{9.9}}{{8.10}}\]
\[ = \frac{{2.3.4.5.6.7.8.9}}{{1.2.3.4.5.6.7.8.}} \cdot \frac{{2.3.4.5.6.7.8.9}}{{3.4.5.6.7.8.9.10}}\]
\[ = \frac{9}{1} \cdot \frac{2}{{10}} = \frac{{9.2}}{{1.10}} = \frac{9}{5}\]
Đáp án cần chọn là: A
Câu 8:
Tính giá trị biểu thức \[A = \left( {\frac{{11}}{4}.\frac{{ - 5}}{9} - \frac{4}{9}.\frac{{11}}{4}} \right).\frac{8}{{33}}\]
 Xem đáp án
Xem đáp án
Ta có: \[A = \left( {\frac{{11}}{4}.\frac{{ - 5}}{9} - \frac{4}{9}.\frac{{11}}{4}} \right).\frac{8}{{33}} = \frac{{11}}{4}.\left( {\frac{{ - 5}}{9} - \frac{4}{9}} \right).\frac{8}{{33}} = \frac{{11}}{4}.\frac{{ - 9}}{9}.\frac{8}{{33}} = \frac{{ - 11}}{4}.\frac{8}{{33}} = \frac{{ - 2}}{3}\]
Đáp án cần chọn là: A
Câu 9:
Tìm số tự nhiên x biết \[\frac{1}{3} + \frac{1}{6} + \frac{1}{{10}} + ... + \frac{1}{{x\left( {x + 1} \right):2}} = \frac{{2019}}{{2021}}\]
 Xem đáp án
Xem đáp án
\[\frac{1}{3} + \frac{1}{6} + \frac{1}{{10}} + ... + \frac{1}{{x\left( {x + 1} \right):2}} = \frac{{2019}}{{2021}}\]
\[2\left[ {\frac{1}{{2.3}} + \frac{1}{{3.4}} + ... + \frac{1}{{x\left( {x + 1} \right)}}} \right] = \frac{{2019}}{{2021}}\]
\(2.\left( {\frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + ... + \frac{1}{x} - \frac{1}{{x + 1}}} \right) = \frac{{2019}}{{2021}}\)
\(2\left( {\frac{1}{2} - \frac{1}{{x + 1}}} \right) = \frac{{2019}}{{2021}}\)
\(1 - \frac{2}{{x + 2}} = \frac{{2019}}{{2021}}\)
\(\frac{2}{{x + 1}} = 1 - \frac{{2019}}{{2021}}\)
\(\begin{array}{l}\frac{2}{{x + 1}} = \frac{2}{{2021}}\\x + 1 = 2021\\x = 2020\end{array}\)
Đáp án cần chọn là: C
Câu 10:
Tìm \[M = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + \frac{1}{{{2^3}}} + ... + \frac{1}{{{2^{99}}}} + \frac{1}{{{2^{100}}}}\]
 Xem đáp án
Xem đáp án
\[\begin{array}{*{20}{l}}{M = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + \frac{1}{{{2^3}}} + ... + \frac{1}{{{2^{99}}}} + \frac{1}{{{2^{100}}}}}\\{2M = 2.\left( {1 + \frac{1}{2} + \frac{1}{{{2^2}}} + \frac{1}{{{2^3}}} + ... + \frac{1}{{{2^{99}}}} + \frac{1}{{{2^{100}}}}} \right)}\\{ = 2 + 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + \frac{1}{{{2^3}}} + ... + \frac{1}{{{2^{99}}}}}\end{array}\]
Ta có:
\[M = 2M - M\]
\[ = \left( {2 + 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + \frac{1}{{{2^3}}} + ... + \frac{1}{{{2^{98}}}} + \frac{1}{{{2^{99}}}}} \right) - \left( {1 + \frac{1}{2} + \frac{1}{{{2^2}}} + \frac{1}{{{2^3}}} + ... + \frac{1}{{{2^{99}}}} + \frac{1}{{{2^{100}}}}} \right)\]
\[ = 2 - \frac{1}{{{2^{100}}}}\]
\[ = \frac{{{2^{101}} - 1}}{{{2^{100}}}}\]
Đáp án cần chọn là: D
Câu 11:
Tính diện tích một hình tam giác biết hai cạnh góc vuông của tam giác đó lần lượt là \(\frac{5}{3}\) cm và \(\frac{7}{4}\) cm?
 Xem đáp án
Xem đáp án
Diện tích hình tam giác đó là: \[S = \frac{1}{2}.\frac{5}{3}.\frac{7}{4} = \frac{{1.5.7}}{{2.3.4}} = \frac{{35}}{{24}}\,c{m^2}\]
Đáp án cần chọn là: C
Câu 12:
Một hình chữ nhật có diện tích \(\frac{{48}}{{35}}\) m2và có chiều dài là \(\frac{6}{5}\) m. Tính chiều rộng của hình chữ nhật đó.
 Xem đáp án
Xem đáp án
Chiều rộng của hình chữ nhật là:
\[\frac{{48}}{{35}}:\frac{6}{5} = \frac{{48}}{{35}}.\frac{5}{6} = \frac{{6.8}}{{7.5}}.\frac{5}{6} = \frac{8}{7}\] (m)
Đáp án cần chọn là: A
Câu 13:
Tính diện tích hình chữ nhật ABCD ở hình sau:
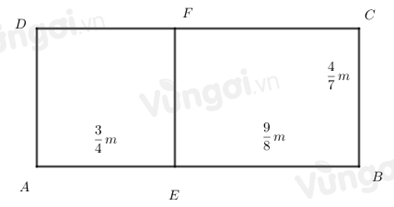
 Xem đáp án
Xem đáp án
Cách 1:
Chiều dài hình chữ nhật ABCD là:
\[\frac{3}{4} + \frac{9}{8} = \frac{{15}}{8}\,(m)\]
Diện tích hình chữ nhật ABCD là:
\[\frac{4}{7}.\frac{{15}}{8} = \frac{{15}}{{14}}({m^2})\]
Cách 2:
Diện tích hình chữ nhật ADFE là:
\[\frac{3}{4}.\frac{4}{7} = \frac{3}{7}({m^2})\]
Diện tích hình chữ nhật BCFE là:
\[\frac{4}{7}.\frac{9}{8} = \frac{9}{{14}}({m^2})\]
Diện tích hình chữ nhật ABCD là:
\[\frac{3}{7} + \frac{9}{{14}} = \frac{{15}}{{14}}({m^2})\]
Đáp án cần chọn là: A
Câu 14:
Tính \[\frac{{28}}{{15}}.\frac{1}{{{4^2}}}.3 + \left( {\frac{8}{{15}} - \frac{{69}}{{60}}.\frac{5}{{23}}} \right):\frac{{51}}{{54}}\]
 Xem đáp án
Xem đáp án
\[\frac{{28}}{{15}}.\frac{1}{{{4^2}}}.3 + \left( {\frac{8}{{15}} - \frac{{69}}{{60}}.\frac{5}{{23}}} \right):\frac{{51}}{{54}}\]
\( = \frac{{28.1.3}}{{{{15.4}^2}}} + \left( {\frac{8}{{15}} - \frac{{23.3}}{{4.3.5}}.\frac{5}{{23}}} \right).\frac{{54}}{{51}}\)
\(\begin{array}{l} = \frac{{7.4.1.3}}{{3.5.4.4}} + \left( {\frac{8}{{15}} - \frac{1}{4}} \right).\frac{{54}}{{51}}\\ = \frac{7}{{20}} + \left( {\frac{{32}}{{60}} - \frac{{15}}{{60}}} \right).\frac{{54}}{{51}}\\ = \frac{7}{{20}} + \frac{{17}}{{60}}.\frac{{54}}{{51}}\\ = \frac{7}{{20}} + \frac{{17}}{{6.10}}.\frac{{6.3.3}}{{17.3}}\\ = \frac{7}{{20}} + \frac{3}{{10}}\\ = \frac{7}{{20}} + \frac{6}{{20}}\\ = \frac{{13}}{{20}}\end{array}\)
Đáp án cần chọn là: D
Câu 15:
Phân số nghịch đảo của số −3 là
 Xem đáp án
Xem đáp án
Phân số nghịch đảo của số −3 là \[\frac{1}{{ - 3}}\]
Đáp án cần chọn là: C
Câu 16:
Kết quả của phép tính \[\frac{{\left( { - 7} \right)}}{6}:\left( { - \frac{{14}}{3}} \right)\] là phân số có tử số là
 Xem đáp án
Xem đáp án
\[\frac{{\left( { - 7} \right)}}{6}:\left( { - \frac{{14}}{3}} \right) = \frac{{ - 7}}{6}.\frac{{ - 3}}{{14}} = \frac{{1.1}}{{2.2}} = \frac{1}{4}\]
Đáp án cần chọn là: D
Câu 17:
Giá trị nào dưới đây của x thỏa mãn \[\left( { - \frac{3}{5}} \right).x = \frac{4}{{15}}\]
 Xem đáp án
Xem đáp án
\[\begin{array}{*{20}{l}}{\left( { - \frac{3}{5}} \right).x = \frac{4}{{15}}}\\{x = \frac{4}{{15}}:\left( {\frac{{ - 3}}{5}} \right)}\\{x = \frac{4}{{15}}.\frac{5}{{ - 3}}}\\{x = - \frac{4}{9}}\end{array}\]
Đáp án cần chọn là: B
Câu 18:
Giá trị biểu thức \[M = \frac{5}{6}:{\left( {\frac{5}{2}} \right)^2} + \frac{7}{{15}}\] là phân số tối giản có dạng \(\frac{a}{b}\) với a >0. Tính b + a.
 Xem đáp án
Xem đáp án
\[M = \frac{5}{6}:{\left( {\frac{5}{2}} \right)^2} + \frac{7}{{15}}\]
\[M = \frac{5}{6}:\frac{{25}}{4} + \frac{7}{{15}}\]
\[M = \frac{5}{6}.\frac{4}{{25}} + \frac{7}{{15}}\]
\[M = \frac{{1.2}}{{3.5}} + \frac{7}{{15}}\]
\[M = \frac{2}{{15}} + \frac{7}{{15}}\]
\[M = \frac{9}{{15}} = \frac{3}{5}\]
Khi đó a = 3, b = 5 nên a + b = 8
Đáp án cần chọn là: A
Câu 19:
Rút gọn \[N = \frac{{\frac{4}{{17}} - \frac{4}{{49}} - \frac{4}{{131}}}}{{\frac{3}{{17}} - \frac{3}{{49}} - \frac{3}{{131}}}}\] ta được
 Xem đáp án
Xem đáp án
\[N = \frac{{\frac{4}{{17}} - \frac{4}{{49}} - \frac{4}{{131}}}}{{\frac{3}{{17}} - \frac{3}{{49}} - \frac{3}{{131}}}} = \frac{{4.\frac{1}{{17}} - 4.\frac{1}{{49}} - 4.\frac{1}{{131}}}}{{3.\frac{1}{{17}} - 3.\frac{1}{{49}} - 3.\frac{1}{{131}}}} = \frac{{4.\left( {\frac{1}{{17}} - \frac{1}{{49}} - \frac{1}{{131}}} \right)}}{{3.\left( {\frac{1}{{17}} - \frac{1}{{49}} - \frac{1}{{131}}} \right)}} = \frac{4}{3}\]
Đáp án cần chọn là: A
Câu 20:
Tìm x biết \[\left( {x + \frac{1}{4} - \frac{1}{3}} \right):\left( {2 + \frac{1}{6} - \frac{1}{4}} \right) = \frac{7}{{46}}\]
 Xem đáp án
Xem đáp án
\[\left( {x + \frac{1}{4} - \frac{1}{3}} \right):\left( {2 + \frac{1}{6} - \frac{1}{4}} \right) = \frac{7}{{46}}\]
\[\left( {x + \frac{1}{4} - \frac{1}{3}} \right):\frac{{23}}{{12}} = \frac{7}{{46}}\]
\[x + \frac{1}{4} - \frac{1}{3} = \frac{7}{{46}}.\frac{{23}}{{12}}\]
\[x + \frac{1}{4} - \frac{1}{3} = \frac{7}{{24}}\]
\[x = \frac{7}{{24}} - \frac{1}{4} + \frac{1}{3}\]
\[x = \frac{3}{8}\]
Đáp án cần chọn là: D
Câu 21:
Giá trị của x thỏa mãn \[\frac{{13}}{{15}} - \left( {\frac{{13}}{{21}} + x} \right).\frac{7}{{12}} = \frac{7}{{10}}\] ?
 Xem đáp án
Xem đáp án
\[\frac{{13}}{{15}} - \left( {\frac{{13}}{{21}} + x} \right).\frac{7}{{12}} = \frac{7}{{10}}\]
\[\left( {\frac{{13}}{{21}} + x} \right).\frac{7}{{12}} = \frac{{13}}{{15}} - \frac{7}{{10}}\]
\[\left( {\frac{{13}}{{21}} + x} \right).\frac{7}{{12}} = \frac{1}{6}\]
\[\frac{{13}}{{21}} + x = \frac{1}{6}:\frac{7}{{12}}\]
\[\frac{{13}}{{21}} + x = \frac{2}{7}\]
\[x = \frac{2}{7} - \frac{{13}}{{21}}\]
\[x = - \frac{1}{3}\]
Đáp án cần chọn là: A
Câu 22:
Số các số nguyên x để \[\frac{{5x}}{3}:\frac{{10{x^2} + 5x}}{{21}}\] có giá trị là số nguyên là
 Xem đáp án
Xem đáp án
\[\frac{{5x}}{3}:\frac{{10{x^2} + 5x}}{{21}} = \frac{{5x}}{3}.\frac{{21}}{{10{x^2} + 5x}} = \frac{{5x.21}}{{3.5x.\left( {2x + 1} \right)}} = \frac{7}{{2x + 1}}\]
Để biểu thức đã cho có giá trị là số nguyên thì \[\frac{7}{{2x + 1}}\] nguyên
Do đó 2x + 1 ∈ Ư(7) = {±1; ±7}
Ta có bảng:

Vậy x ∈ {0; −1; 3; −4} suy ra có 4 giá trị thỏa mãn.
Đáp án cần chọn là: B
Câu 23:
Một người đi xe máy, đi đoạn đường AB với vận tốc 40km/h hết \(\frac{5}{4}\) giờ. Lúc về, người đó đi với vận tốc 45km/h. Tính thời gian người đó đi từ B về A?
 Xem đáp án
Xem đáp án
Quãng đường AB là: \[40.\frac{5}{4} = 50\] (km)
Thời gian người đó đi từ B về A là: \[\frac{{50}}{{45}} = \frac{{10}}{9}\] (giờ)
Đáp án cần chọn là: A
Câu 24:
Phân số \(\frac{a}{b}\) là phân số lớn nhất mà khi chia mỗi phân số \(\frac{{12}}{{35}};\frac{{18}}{{49}}\) cho \(\frac{a}{b}\) ta được kết quả là một số nguyên. Tính a + b.
 Xem đáp án
Xem đáp án
Gọi phân số lớn nhất cần tìm là: \[\frac{a}{b}\] (a;b là nguyên tố cùng nhau)
Ta có: \[\frac{{12}}{{35}}:\frac{a}{b} = \frac{{12b}}{{35{\rm{a}}}}\] là số nguyên, mà 12; 35 là nguyên tố cùng nhau
Nên 12 ⋮ a; b ⋮ 3
Ta lại có: \[\frac{{18}}{{49}}:\frac{a}{b} = \frac{{18b}}{{49{\rm{a}}}}\] là số nguyên, mà 18 và 49 nguyên tố cùng nhau
Nên 18 ⋮ a; b ⋮ 49
Để \[\frac{a}{b}\] lớn nhất ta có a = UCLN(12; 18) = 6a và b = BCNN(35; 49)= 245b
Vậy tổng a + b = 6 + 245 = 251
Đáp án cần chọn là: B
Câu 25:
Tính giá trị biểu thức:
\[\left( {\frac{{ - 2}}{{ - 5}}:\frac{3}{{ - 4}}} \right).\frac{4}{5}\]
 Xem đáp án
Xem đáp án
\[\left( {\frac{{ - 2}}{{ - 5}}:\frac{3}{{ - 4}}} \right).\frac{4}{5} = \left( {\frac{2}{5}.\frac{{ - 4}}{3}} \right).\frac{4}{5} = \frac{{ - 8}}{{15}}.\frac{4}{5} = \frac{{ - 32}}{{75}}\]
Đáp án cần chọn là: C
