Bài 18: Hình tam giác đều. hình vuông. hình lục giác đều
-
1618 lượt thi
-
40 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Có bao nhiêu tính chất dưới đây là của hình vuông?
i) Hình vuông có bốn cạnh bằng nhau.
ii) Hình vuông có bốn góc bằng nhau và bằng .
iii) Hình vuông có hai đường chéo bằng nhau.
 Xem đáp án
Xem đáp án
Đáp án C
Trong hình vuông:
- Bốn cạnh bằng nhau.
- Bốn góc bằng nhau và bằng .
- Hai đường chéo bằng nhau.
Suy ra i) và iii) là tính chất của hình vuông.
Vậy có 2 tính chất thỏa mãn của hình vuông.
Câu 3:
Trong các hình vẽ dưới đây, Có bao nhiêu hình là hình lục giác đều?

 Xem đáp án
Xem đáp án
Đáp án D
Hình 1) là hình các viên gạch lục giác đều.
Hình 2) là hộp mứt tết cổ truyền có dạng hình lục giác đều.
Hình 3) là tổ ong có dạng hình lục giác đều.
Hình 4) là khay đựng bánh kẹo có dạng hình lục giác đều.
Vậy cả 4 hình đều là hình lục giác đều.
Câu 4:
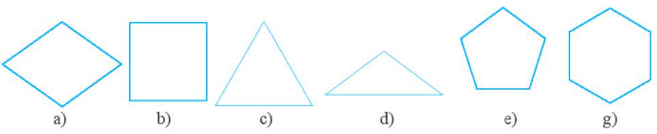
Quan sát các hình dưới đây và cho biết hình nào là hình vuông, hình nào là hình tam giác đều, hình nào là hình lục giác đều?
 Xem đáp án
Xem đáp án
Đáp án D
Quan sát hình vẽ và tiến hành đo ta thấy:
- Hình vuông: b;
- Hình tam giác đều: c;
- Hình lục giác đều: g.
Câu 5:
Hình lục giác đều có bao nhiêu đường chéo?
 Xem đáp án
Xem đáp án
Đáp án C
Hình lục giác đều có tất cả ba đường chéo.
Câu 6:
Trong các hình dưới đây (H.4.1), hình nào là tam giác đều?
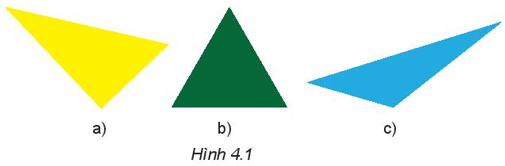
Em hãy tìm một số hình ảnh hình tam giác đều trong thực tế.
 Xem đáp án
Xem đáp án
+) Trong các hình dưới đây (H.4.1), hình b) là tam giác đều.
+) Một số hình ảnh tam giác đều trong thực tế: một mặt của rubik tam giác; kệ sách; …

Câu 7:
Hình nào có số cạnh ít nhất trong các hình sau:
 Xem đáp án
Xem đáp án
Đáp án A
- Số cạnh của tam giác đều là 3;
- Số cạnh của hình vuông là: 4;
- Số cạnh của hình lục giác đều là: 6;
Câu 8:
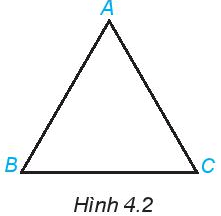
Cho tam giác đều ABC như Hình 4.2
1. Gọi tên các đỉnh, cạnh, góc của tam giác đều ABC.
2. Dùng thước thẳng để đo và so sánh các cạnh của tam giác ABC.
3. Sử dụng thước đo góc để đo và so sánh các góc của tam giác ABC.
 Xem đáp án
Xem đáp án
1. Trong hình 4.2, tam giác đều ABC có:
+) Các đỉnh: A, B, C
+) Các cạnh: AB, BC, AC
+) Các góc: góc A, góc B, góc C
2. Khi sử dụng thước thẳng để đo ta nhận thấy: AB = BC = AC, nghĩa là các cạnh của tam giác ABC bằng nhau.
3. Khi sử dụng thước đo góc là ê ke để đo ta nhận thấy góc A, góc B, góc C đều bằng , tức là các góc của tam giác ABC bằng nhau và bằng .
Câu 9:
Phát biểu nào dưới đây là sai?
 Xem đáp án
Xem đáp án
Đáp án C
Hình tam giác đều không có đường chéo nên phát biểu C là sai.
Câu 10:
1. Vẽ tam giác đều ABC cạnh 3cm theo hướng dẫn sau:
Bước 1. Vẽ đoạn thẳng AB = 3 cm.
Bước 2. Dùng ê ke có góc vẽ góc BAx bằng .
. Ta thấy Ax và By cắt nhau tại C, ta được tam giác đều ABC.
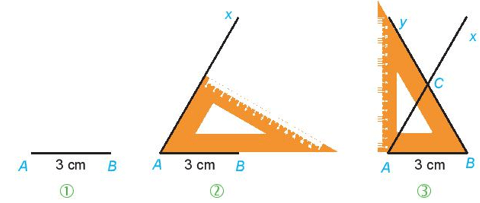
2. Em hãy kiểm tra lại hình vừa vẽ, xem các cạnh của tam giác ABC có bằng nhau không? Các góc có bằng nhau không?
 Xem đáp án
Xem đáp án
1. Thực hành vẽ theo hướng dẫn trên.
2. Sau khi vẽ xong ta kiểm tra lại hình đã vẽ ta nhận thấy:
+) AB = AC = BC = 3cm nghĩa là các cạnh của tam giác ABC bằng nhau
+) Các góc A, góc B, góc C bằng , tức là các góc của tam giác ABC bằng nhau và bằng .
Câu 11:
Sắp xếp các bước vẽ hình tam giác đều cạnh 2cm:
1) Vẽ đường tròn tâm A bán kính 2cm và đường tròn tâm B bán kính 2cm.
2) Vẽ đoạn thẳng AB bằng 2cm.
3) Nối các điểm A với C, B với C ta được tam giác đều ABC cạnh 2 cm.
4) Hai đường tròn tâm A và tâm B cắt nhau tại điểm C.
 Xem đáp án
Xem đáp án
Đáp án D
Các bước để vẽ tam giác đều như sau:
2) Vẽ đoạn thẳng AB bằng 2cm.
1) Vẽ đường tròn tâm A bán kính 2cm và đường tròn tâm B bán kính 2cm.
4) Hai đường tròn tâm A và tâm B cắt nhau tại điểm C.
3) Nối các điểm A với C, B với C ta được tam giác đều ABC cạnh 2 cm.
Câu 12:
Em hãy tìm một số hình ảnh của hình vuông trong thực tế.
 Xem đáp án
Xem đáp án
Một số hình ảnh của hình vuông trong thực tế: các mặt của xúc xắc, đĩa, gạch lát nền; …

Câu 13:
Trong hình dưới đây có bao nhiêu hình vuông?
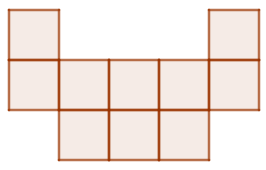
 Xem đáp án
Xem đáp án
Đáp án C
Có 10 hình vuông nhỏ
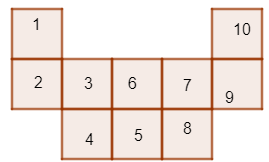
Và hai hình vuông vừa:
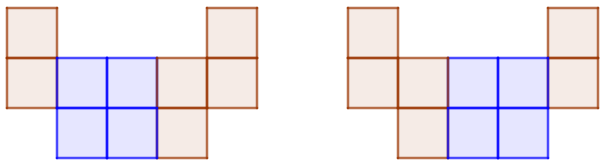
Vậy tổng cộng có 12 hình vuông.
Câu 14:
Hình lục giác đều được ghép từ:
 Xem đáp án
Xem đáp án
Đáp án C
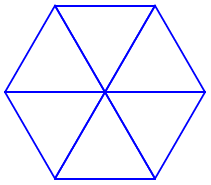
Ta thấy hình lục giác đều được ghép từ 6 tam giác đều.
Câu 15:
Phát biểu nào dưới đây là sai?
 Xem đáp án
Xem đáp án
Đáp án A
Nếu tam giác MNP có ba cạnh MN = NP = PQ thì tam giác MNP đều hoặc nếu tam giác MNP có ba góc M, góc N, góc P đều bằng 600 thì tam giác MNP đều. Do đó B, C đúng.
Còn nếu tam giác MNP chỉ có hai cạnh bằng nhau thì chưa chắc là tam giác đều. Do đó D đúng và A sai.
Câu 16:
Nối cột A với cột B để được các bước vẽ hình vuông 7cm một cách chính xác:
Cột A |
| Cột B |
1) Bước 1 | a) Vẽ đường thẳng đi qua B vuông góc với AB. Trên đường thẳng này lấy điểm C sao cho BC bằng 7cm. | |
2) Bước 2 | b) Nối điểm B với điểm C lại ta được hình vuông ABCD cạnh 7cm. | |
3) Bước 3 | c) Vẽ cạnh AB bằng 7cm | |
4) Bước 4 | d) Vẽ đường thẳng đi qua A vuông góc với AB. Trên đường thẳng này lấy điểm D sao cho AD bằng 7cm |
 Xem đáp án
Xem đáp án
Đáp án A

Vậy 1 – c; 2 – a; 3 – d; 4 – b.
Chú ý: Giữa hai bước 3 và bước 4 có thể thức hiện bước nào trước cũng được.
Câu 17:
Hình lục giác đều có đường chéo chính dài 18 cm. Số đo cạnh của hình lục giác đều là:
 Xem đáp án
Xem đáp án
Đáp án D
Do hình lục giác được ghép từ 6 tam giác đều như sau:
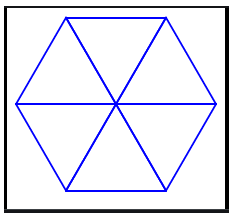
Do đó cạnh tam giác đều bằng: 18:2 = 9cm.
Mà cạnh của tam giác đều cũng chính là cạnh của hình lục giác đều.
Vậy số đo cạnh của hình lục giác đều có đường chéo chính dài 18cm là: 9cm.
Câu 18:
Quan sát Hình 4.3a.
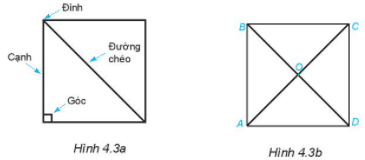
1. Nêu tên các đỉnh, cạnh, đường chéo của hình vuông ABCD (H.4.3b)
2. Dùng thước thẳng đo và so sánh độ dài các cạnh của hình vuông; hai đường chéo của hình vuông.
3. Dùng thước đo góc để đo và so sánh các góc của hình vuông.
 Xem đáp án
Xem đáp án
1. Hình vuông ABCD có
Các đỉnh: A, B, C, D
Các cạnh: AB, BC, CD, DA
Các đường chéo: AC, BD
2. Sau khi dùng thước thẳng đo ta nhận thấy:
+) AB = BC = CD = AD nghĩa là độ dài các cạnh của hình vuông đều bằng nhau.
+) AC = BD, nghĩa là độ dài 2 đường chéo của hình vuông bằng nhau.
3. Sau khi sử dụng thước đo góc là ê ke để đo ta nhận thấy: các góc A, góc B, góc C, góc D đều bằng 90o nghĩa là các góc của hình vuông đều bằng nhau và bằng .
Câu 19:
1. Vẽ hình vuông ABCD có cạnh 4 cm theo hướng dẫn sau:
Bước 1. Vẽ đoạn thẳng AB = 4 cm.
Bước 2. Vẽ đường thẳng vuông góc với AB tại A. Xác định điểm D trên đường thẳng đó sao cho AD = 4 cm.
Bước 3. Vẽ đường thẳng vuông góc với AB tại B. Xác định điểm C trên đường thẳng đó sao cho BC = 4 cm.
Bước 4. Nối C với D ta được hình vuông ABCD
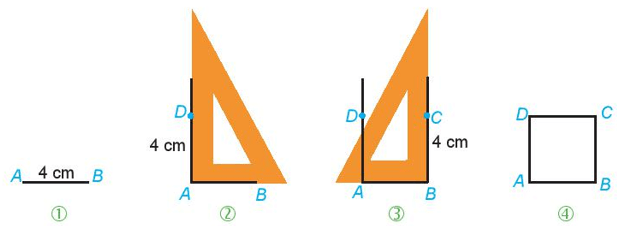
2. Em hãy kiểm tra lại hình vừa vẽ, xem các cạnh có bằng nhau không? Các góc có bằng nhau không?
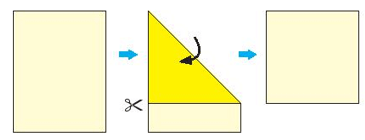
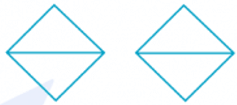
3. a) Hãy gấp và cắt một hình vuông từ tờ giấy hình chữ nhật như hình bên.
b) Cắt hình vuông đó theo hai đường chéo thành phần rồi ghép thành hai hình vuông.
 Xem đáp án
Xem đáp án
1. Thực hành vẽ theo hướng dẫn trên.
2. Sau khi thực hành vẽ hình theo 4 bước, ta nhận thấy:
+) AB = BC = CD = AD nghĩa là độ dài các cạnh của hình vuông đều bằng nhau.
+) Các góc A, góc B, góc C, góc D đều bằng , nghĩa là các góc của hình vuông đều bằng nhau và bằng .
3. a) Em chuẩn bị giấy, kéo và thực hiện như sau:

b) Cắt hình vuông theo hai hình chéo để được bốn tam giác.

+) Ghép lại để được hai hình vuông như sau:
Câu 20:
1. Cắt sáu hình tam giác đều giống nhau và ghép lại như Hình 4.4a để được hình lục giác đều như Hình 4.4b.

2. Kể tên các đỉnh, cạnh, góc của hình lục giác đều ABCDEF.
3. Các cạnh của hình này có bằng nhau không?
4. Các góc của hình này có bằng nhau không và bằng bao nhiêu độ?
 Xem đáp án
Xem đáp án
1. Thực hành cắt như hình.
2. Trong hình lục giác đều ABCDEF có:
+) Các đỉnh: A, B, C, D, E, F
+) Các cạnh: AB, BC, CD, DE, EF, FA
+) Các góc: góc A, góc B, góc C, góc D, góc E, góc F
3. Ta thấy AB = BC = CD = DE = EF = FA, nghĩa là các cạnh của hình này bằng nhau
4. Ta thấy các góc A, góc B, góc C, góc D, góc E, góc F đều bằng , nghĩa là các góc của hình bằng nhau và bằng .
Câu 21:
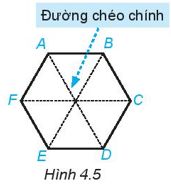
Hãy quan sát Hình 4.5.
1. Hãy kể tên các đường chéo chính của hình lục giác đều ABCDEF.
2. Hãy so sánh độ dài các đường chéo chính với nhau.
 Xem đáp án
Xem đáp án
1. Các đường chéo chính của hình: AD, BE, CF
2. Dùng thước thẳng đo, ta thấy AD = BE = CF hay độ dài các đường chéo chính bằng nhau.
Câu 22:
Cho hình lục giác đều như hình 4.6
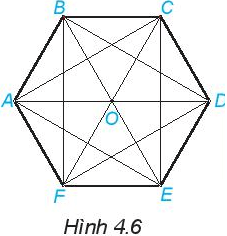
Ta đã biết, 6 hình tam giác đều ghép lại thành hình lục giác đều, đó là những tam giác đều nào? Ngoài 6 tam giác đều đó, trong hình em còn thấy những tam giác đều nào khác?
 Xem đáp án
Xem đáp án
+) Các tam giác đều ghép thành hình lục giác đều là: tam giác ABO, tam giác BCO, tam giác CDO, tam giác DEO, tam giác EFO, tam giác FAO
+) Trong hình còn có các tam giác đều là: tam giác ACE (vì có AC = AE = CE), tam giác BDF (vì có BD = DF = BF)
Câu 23:
Hãy tìm một số hình ảnh có dạng hình lục giác đều trong thực tế.
 Xem đáp án
Xem đáp án
Một số hình ảnh có dạng hình lục giác đều trong thực tế: Gạch lát ốp tường, khay đựng kẹo, đèn thả, mái đền, …

Câu 24:
Qua tìm hiểu về hình tam giác đều, hình vuông, hình lục giác đều, em có nhận xét gì về đặc điểm chung (cạnh, góc) của các hình nói trên?
 Xem đáp án
Xem đáp án
Đặc điểm chung của các hình tam giác đều, hình vuông, hình lục giác đều là các cạnh bằng nhau, các góc bằng nhau.
Câu 25:
Mặt trên của một cái bánh có dạng hình lục giác đều (như hình bên). Em hãy cắt bánh để chia đều cho:
a) 6 bạn
b) 12 bạn
c) 4 bạn

 Xem đáp án
Xem đáp án
a) Vì mặt trên của một bánh có dạng hình lục giác đều. Để cắt bánh chia đều cho 6 bạn, ta có thể chia thành 6 tam giác đều bằng nhau như hình vẽ sau:
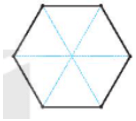
b) Vì mặt trên của một bánh có dạng hình lục giác đều. Để cắt bánh chia đều cho 12 bạn, ta có thể chia thành 12 tam giác bằng nhau như hình vẽ sau:
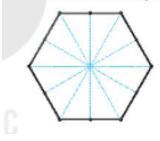
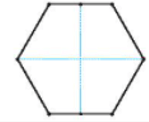
c) Vì mặt trên của một bánh có dạng hình lục giác đều. Để cắt bánh chia đều cho 4 bạn ta có thể làm như sau:
Câu 26:
Hãy kể tên một số vật dụng, họa tiết, công trình kiến trúc, …có hình ảnh của hình tam giác đều, hình vuông, hình lục giác đều.
 Xem đáp án
Xem đáp án
Một số vật dụng, họa tiết, công trình kiến trúc, ... có hình ảnh:
+) Tam giác đều: biển báo giao thông, giá đựng sách, ...
+) Hình vuông: khuôn bánh chưng, gạch đá hoa, cửa sổ, ...
+) Hình lục giác đều: bề mặt tổ ong có cấu trúc là các hình lục giác đều xếp liền nhau, mặt một số loại hộp bánh, mái đền, gạch lát nền, ...
Câu 27:
Vẽ hình tam giác đều có cạnh bằng 2 cm.
 Xem đáp án
Xem đáp án
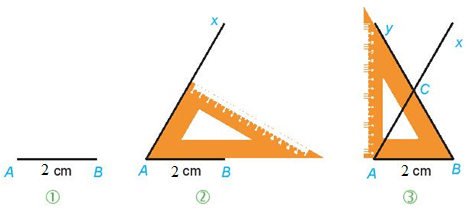
Vẽ tam giác đều ABC cạnh 2 cm theo hướng dẫn sau:
Bước 1. Vẽ đoạn thẳng AB = 2 cm.
Bước 2. Dùng ê ke có góc vẽ góc BAx bằng .
Bước 3. Vẽ góc ABy bằng . Ta thấy Ax và By cắt nhau tại C, ta được tam giác đều ABC.
Câu 28:
Vẽ hình vuông có cạnh bằng 5 cm.
 Xem đáp án
Xem đáp án
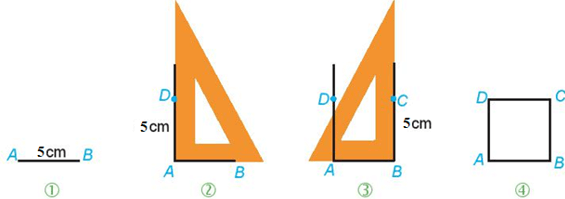
Bước 1. Vẽ đoạn thẳng AB = 5 cm.
Bước 2. Vẽ đường thẳng vuông góc với AB tại A. Xác định điểm D trên đường thẳng đó sao cho AD = 5 cm.
Bước 3. Vẽ đường thẳng vuông góc với AB tại B. Xác định điểm C trên đường thẳng đó sao cho BC = 5 cm.
Bước 4. Nối C với D ta được hình vuông ABCD.
Câu 29:
Cắt và ghép để được một cái hộp có nắp theo hình gợi ý dưới đây:

 Xem đáp án
Xem đáp án
1. Cắt như hình vẽ
2.
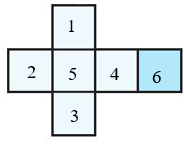
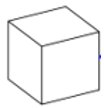
Gập 3 hình vuông 1, 2, 3, 4 theo cạnh kề với cạnh hình vuông 5 rồi gập hình vuông 6 sao cho có 1 cạnh kề với cạnh của hình vuông 1, 2, 3, 4 ta được hình lập phương.
Câu 30:
Có nhiều cách để trang trí một hình vuông, chẳng hạn như hình dưới. Em hãy vẽ một hình vuông trên tờ giấy A4 và trang trí theo cách của mình.

 Xem đáp án
Xem đáp án
Học sinh được thoải mái trang trí hình vuông theo ý tưởng của mình.
Dưới đây là một hình trang trí minh họa:

Câu 31:
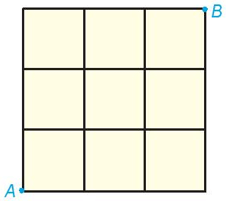
Quan sát hình dưới và chỉ ra ít nhất hai cách, để một con kiến bò từ A đến B theo đường chéo của các hình vuông nhỏ?
 Xem đáp án
Xem đáp án
Có nhiều cách để con kiến bò từ A đến B theo đường chéo của hình vuông.
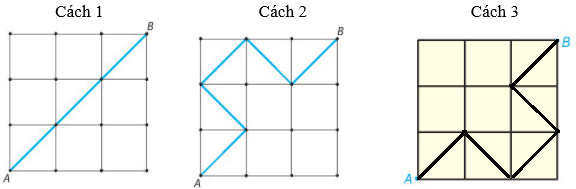
Dưới đây là ba cách:
Câu 32:
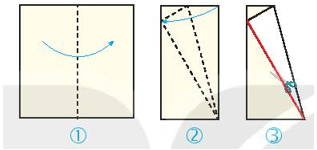
Gấp và cắt hình tam giác đều từ một tờ giấy hình vuông theo hướng dẫn sau
 Xem đáp án
Xem đáp án
Học sinh gấp và cắt theo hướng dẫn.
Bước 1: Chuẩn bị 1 tờ giấy hình vuông, gấp đôi tờ giấy từ trái sang.
Bước 2: Từ đỉnh trên cùng bên phải gấp vào mép cạnh hình vuông sao cho nó khớp với đỉnh ở bên dưới
Bước 3: Dùng kéo cắt theo cạnh màu đỏ trên hình
Câu 33:
Người ta muốn đặt một trạm biến áp để đưa điện về sáu ngôi nhà. Phải đặt trạm biến áp ở đâu để khoảng cách từ trạm biến áp đến sáu ngôi nhà bằng nhau, biết rằng sáu ngôi nhà ở vị trí sáu đỉnh của hình lục giác đều?
 Xem đáp án
Xem đáp án
Vị trí đặt trạm biến áp là giao điểm các đường chéo chính của hình lục giác đều.
Gọi hình lục giác đều là ABCDEF, O là giao điểm của các đường chéo chính. Khi đó ta có 6 tam giác đều là: AOB, BOC, COD, DOE, EOF, AOF. Do đó mà OA = OB = OC = OD = OE = OF hay O cách đều các đỉnh của hình lục giác đều
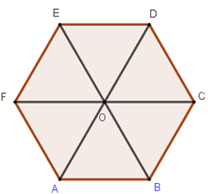
Vậy trạm biến áp đặt ở điểm O thì để khoảng cách từ trạm biến áp đến sáu ngôi nhà bằng nhau vì 6 ngôi nhà đặt ở các đỉnh của hình lục giác đều.
Câu 34:
Vẽ hình vuông ABCD có cạnh bằng 5cm.
 Xem đáp án
Xem đáp án
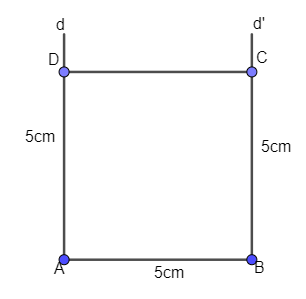
Bước 1. Vẽ đoạn thẳng AB = 5cm;
Bước 2. Qua A dựng đường thẳng d vuông góc với AB, qua B dựng đường thẳng d’ vuông góc với AB.
Bước 3. Trên đường thẳng d lấy điểm D sao cho AD = 5cm, trên d’ lấy điểm C sao cho BC = 5cm.
Bước 4. Nối D với C ta được hình vuông ABCD.
Câu 35:
Hãy quan sát hình vẽ:
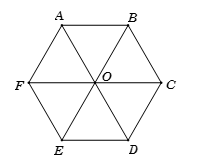
a) Hãy kể tên các đường chéo chính của hình lục giác đều ABCDEF.
b) Hãy so sánh độ dài các đường chéo chính với nhau.
 Xem đáp án
Xem đáp án
a) Các đường chéo chính của hình lục giác đều ABCDEF là: AD, BE, CF.
b) Sau khi đo độ dài ta thấy AD = BE = CF = 2,1 cm.
Câu 36:
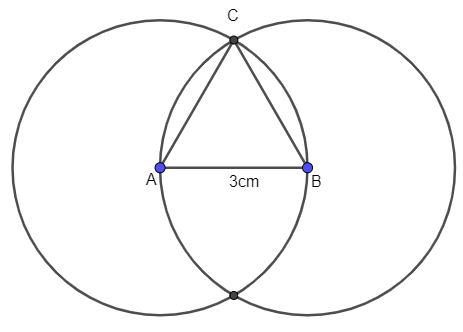
Vẽ tam giác đều cạnh 3cm.
 Xem đáp án
Xem đáp án
Bước 1. Vẽ đoạn thẳng AB = 3cm.
Bước 2. Dùng compa vẽ đường tròn tâm A bán kính 3cm và đường tròn tâm B bán kính 3 cm.
Bước 3. Hai đường tròn này giao nhau tại C. Nối A với C, B với C ta được tam giác ABC đều.
Câu 37:
Người ta muốn đặt một trạm biến áp để đưa điện về sáu ngôi nhà. Phải đặt trạm biến áp ở đâu để khoảng cách từ trạm biến áp đến sáu ngôi nhà đều bằng nhau, biết rằng sáu ngôi nhà ở vị trí sáu đỉnh của lục giác đều.
 Xem đáp án
Xem đáp án
Phải đặt trạm biến áp ở tâm O hình lục giác đều tạo bởi sáu ngôi nhà.
Vì độ dài các đường chéo chính của hình lục giác đều bằng nhau, mà O là trung điểm của các đường chéo đó nên khoảng cách từ tâm O đến các đỉnh của lục giác đều là bằng nhau hay nếu đặt trạm biến áp ở O thì khoảng cách từ trạm biến áp đến sáu ngôi nhà đều bằng nhau.
Câu 38:
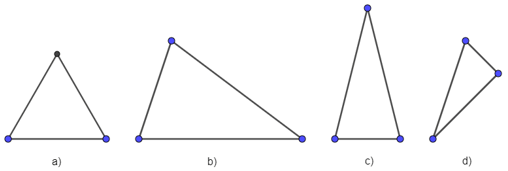
Hình nào dưới đây là hình biểu diễn tam giác đều?
 Xem đáp án
Xem đáp án
Đáp án A
Trong các hình trên: Hình a) là hình biểu diễn tam giác đều.
Câu 39:
Cho phát biểu sau: “……….. là hình có ba cạnh bằng nhau và ba góc bằng nhau bằng . Điền từ thích hợp vào chỗ trống.
 Xem đáp án
Xem đáp án
Đáp án C
Tam giác đều là hình có ba cạnh bằng nhau và ba góc bằng nhau bằng .
Câu 40:
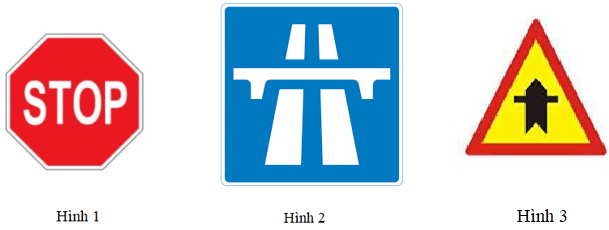
Cho các biển báo giao thông dưới đây:
Phát biểu nào dưới đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án D
Hình 1 là biển báo dừng lại có hình lục giác đều. Do đó A đúng.
Hình 2 là biển báo chỉ đường có hình vuông. Do đó B đúng.
Hình 3 là biển báo đường giao nhau có hình tam giác đều. Do đó C đúng.
Vậy cả A, B và C đều đúng.
