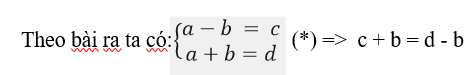Các dạng bài tập nâng cao về số nguyên tố cực hay, có lời giải
-
1906 lượt thi
-
13 câu hỏi
-
25 phút
Danh sách câu hỏi
Câu 1:
Chứng minh rằng các số sau đây là hợp số:
a)
 Xem đáp án
Xem đáp án
a) Ta có:
Theo quy ước ta có:
có chữ số tận cùng là 8
có chữ số tận cùng là 7
luôn có chữ số tận cùng là 5
có chữ số tận cùng là 7
luôn có chữ số tận cùng là 1
Ta có: có chữ số tận cùng là 8
Suy ra chia hết cho 2.
Vậy, đây là hợp số.
Câu 2:
Chứng minh rằng các số sau đây là hợp số:
b)
 Xem đáp án
Xem đáp án
b) Ta có :
có chữ số tận cùng là 1
có chữ số tận cùng là 1 ( các số có chữ số tận cùng là 3 khi nâng lên lũy thừa bậc 4n (n là số tự nhiên) thì có chữ số tận cùng là 1. Số đã cho có số mũ là 124 = 4.31)
luôn có chữ số tận cùng là 5
Nên có chữ số tận cùng là 8
suy ra chia hết cho 2.
vậy, đây là hợp số.
Câu 3:
Chứng minh rằng nếu ba số a, a+k, a+2k đều là các số nguyên tố lớn hơn 3, thì k chia hết cho 6
 Xem đáp án
Xem đáp án
Do a, a + k, a + 2k đều là nguyên tố lớn hơn 3 nên đều là số lẻ và không chia hết cho 3.
• Vì a và a + k cùng lẻ nên a + k - a = k ⋮ 2. (1)
• Vì a, a + k, a + 2k đều không chia hết cho 3 nên khi chia cho 3 ít nhất hai số có cùng số dư, khi đó:
+ Nếu a và a + k có cùng số dư, thì suy ra: (a+k) - a = k ⋮ 3
+ Nếu a và a + 2k có cùng số dư, thì suy ra:
( a + 2k ) - a = 2k 3 nhưng (2,3) = 1 nên k 3
Vậy, ta luôn có k chia hết cho 3 (2)
Từ (1),(2) và do (2,3)=1 ta suy ra k ⋮ 6, đpcm.
Nhận xét: Trong lời giải trên, ta đã định hướng được rằng để chứng minh k ⋮ 6 thì cần chứng minh k ⋮ 2 và k ⋮ 3 và ở đó:
• Việc chứng minh k ⋮ 2 được đánh giá thông qua nhận định a, a + k,a + 2k đều là nguyên tố lẻ hơn kém nhau k đơn vị.
• Việc chứng minh k ⋮ 3 được đánh giá thông qua nhận định “ba số lẻ không chia hết cho 3 thì có ít nhất hai số có cùng số dư” và như vậy hiệu của hai số đó sẽ chia hết cho 3.
Câu 4:
Ta biết rằng có 25 số nguyên tố nhỏ hơn 100. Tổng của 25 số nguyên tố đó là số chẵn hay lẻ?
 Xem đáp án
Xem đáp án
Ta thấy trong 25 số nguyên tố có 1 số chẵn còn lại là 24 số lẻ. Tổng của 24 số lẻ là một số chẵn nên tổng của 25 số nguyên tố nhỏ hơn 100 là số chẵn.
Câu 5:
Tổng của ba số nguyên tố bằng 1012. Tìm số nhỏ nhất trong ba số nguyên tố đó.
 Xem đáp án
Xem đáp án
Vì tổng của 3 số nguyên tố bằng 1012, nên trong 3 số nguyên tố đó tồn tại một số nguyên tố chẵn. Mà số nguyên tố chẵn duy nhất là 2 và là số nguyên tố nhỏ nhất. Vậy số nguyên tố nhỏ nhất trong 3 số nguyên tố đó là 2
Câu 6:
Tìm bốn số nguyên tố liên tiếp, sao cho tổng của chúng là số nguyên tố.
 Xem đáp án
Xem đáp án
Tổng của 4 số nguyên tố là một số nguyên tố ⇒ tổng của 4 số nguyên tố là 1 số lẻ ⇒ trong 4 số đó tồn tại ít nhất một số nguyên tố chẵn. Mà số nguyên tố chẵn duy nhất là 2. Vậy 4 số nguyên tố cần tìm là: 2; 3; 5; 7
Câu 7:
Tổng của hai số nguyên tố có thể bằng 2003 được không?
 Xem đáp án
Xem đáp án
Vì tổng của 2 số nguyên tố bằng 2003, nên trong 2 số nguyên tố đó tồn tại 1 số nguyên tố chẵn. Mà số nguyên tố chẵn duy nhất là 2. Do đó số nguyên tố còn lại là 2001. Do 2001 chia hết cho 3 và 2001 > 3. Suy ra 2001 không phải là số nguyên tố. ⇒ Tổng của hai số nguyên tố không thể bằng 2003 .
Câu 8:
Tìm hai số nguyên tố, sao cho tổng và hiệu của chúng đều là số nguyên tố.
 Xem đáp án
Xem đáp án
Gọi a, b, c, d là các số nguyên tố. (a>b)
Từ (*) ⇒ a > 2, a là số nguyên tố lẻ ⇒ c + b và d – b là số lẻ. Do b, c, d đều là số nguyên tố nên để c + b và d – b là số lẻ thì ⇒ b chẵn. Vậy b = 2
a. Bài toán đưa về dạng tìm một số nguyên tố a sao cho a – 2 và a + 2 cũng là số nguyên tố.
- Nếu a = 5 ⇒ a – 2 = 3; a + 2 = 7 đều là số nguyên tố
- Nếu a ≠ 5 . Xét 2 trường hợp
+ a chia 3 dư 1 ⇒ a + 2 chia hết cho 3 : không là số nguyên tố
+ a chia 3 dư 2 ⇒ a – 2 chia hết cho 3: không là số nguyên tố
Vậy chỉ có số nguyên tố a duy nhất thoả mãn là 5.
Hai số nguyên tố cần tìm là 5; 2
Câu 9:
Tìm số nguyên tố có ba chữ số, biết rằng nếu viết số đó theo thứ tự ngược lại thì ta được một số là lập phương của một số tự nhiên.
 Xem đáp án
Xem đáp án
Gọi số tự nhiên đó là a.
Ta có 103 = 1000; 53 = 125 ⇒ 125 ≤ a 3 < 1000 ⇒ 5 ≤ a < 10
Ta có bảng sau:
| a | 5 | 6 | 7 | 8 | 9 |
| a3 | 125 | 216 | 343 | 512 | 729 |
| Số cần tìm | 521 | 612 | 343 | 215 | 927 |
| Kết luận | TM | loại | loại | loại | loại |
Vậy số cần tìm là 521
Câu 10:
Cho p là số nguyên tố lớn hơn 3. Biết p + 2 cũng là số nguyên tố. Chứng minh rằng p + 1 chia hết cho 6.
 Xem đáp án
Xem đáp án
Vì p là số nguyên tố lớn hơn 3 nên p có dạng 6k-1 hoặc 6k+1nếu p=6k+1 thì p+2=6k+3=3(2k+1)chia hết cho 3 và lớn hơn 3 nên là hợp số(vô lí) do đó p=6k-1⇒p+1=6k chia hết cho 6(đpcm)
Câu 11:
Một số nguyên tố p chia cho 42 có số dư r là hợp số. Tìm số dư r.
 Xem đáp án
Xem đáp án
Ta có:
p = 42.k + r. = 2.3.7.k + r
Vì r là hợp số và r < 42 nên r phải là tích của 2 số r = x.y
x và y không thể là 2, 3, 7 và cũng không thể là số chia hết cho 2, 3, 7 được vì nếu thế thì p không là số nguyên tố.
Vậy x và y có thể là các số trong các số {5,11,13, ..}
Nếu x=5 và y=11 thì r = x.y =55 > 42
Vậy chỉ còn trường hợp x = 5, y = 5. Khi đó r = 25
Câu 12:
Hai số nguyên tố sinh đôi là hai số nguyên tố hơn kém nhau 2 đơn vị. Tìm hai số nguyên tố sinh đôi nhỏ hơn 50.
 Xem đáp án
Xem đáp án
Các số nguyên tố sinh đôi nhỏ hơn 50 là:3 và 5; 5 và 7; 11 và 13; 17 và 19; 29 và 31; 41 và 43.
Câu 13:
Tìm số nguyên tố, biết rằng số đó bằng tổng của hai chữ số nguyên tố và bằng hiệu của hai số nguyên tố.
 Xem đáp án
Xem đáp án
Giả sử a, b, c, d, e là các số nguyên tố (d > e)
Theo bài ra ta có: a = b + c = d – e (*)
Từ (*) ⇒ a > 2 ⇒ a là số nguyên tố lẻ
+ b + c = d – e là số lẻ.do b, d là các số nguyên tố ⇒ b, d là số lẻ ⇒ c, e là số chẵn.
+ c = e = 2 (do e, c là các số nguyên tố)
+ a = b + 2 = d – 2 ⇒ d = b + 4,vậy ta cần tìm số nguyên tố b sao cho b + 2, b + 4 cũng là số nguyên tố
+ b = 3
Vậy số nguyên tố cần tìm là 5