Bài 19: hình chữ nhật. Hình thoi hình bình hành. Hình thang cân
-
1022 lượt thi
-
41 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Em hãy tìm một số hình ảnh của hình chữ nhật trong thực tế.
 Xem đáp án
Xem đáp án
Ví dụ: màn hình ti vi, một mặt tủ lạnh, mặt hộp đựng thức ăn, mặt bàn, cửa sổ, quyển sách, tấm lót chuột, cái cặp sách, màn hình máy tính, khung ảnh, …
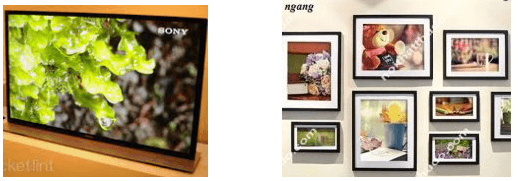
Câu 2:
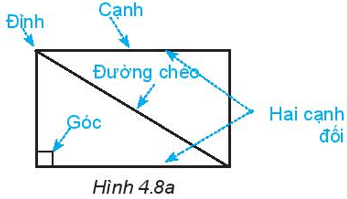
Quan sát hình chữ nhật ở Hình 4.8a.
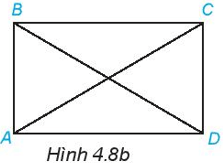
1. Nêu tên đỉnh, cạnh, đường chéo, hai cạnh đối của hình chữ nhật ABCD (H.4.8b)
2. Dùng thước đo góc để đo và so sánh các góc của hình chữ nhật ABCD.
3. Dùng thước thẳng hoặc compa để so sánh hai cạnh đối, hai đường chéo của hình chữ nhật ABCD.
 Xem đáp án
Xem đáp án
1. Với hình chữ nhật ABCD trên Hình 4.8b, ta có:
+) Các đỉnh: A, B, C, D
+) Các cạnh: AB, BC, CD, DA
+) Các đường chéo: AC, BD
+) Hai cạnh đối: AB và CD; BC và AD
2. Sau khi sử dụng thước đo góc ta nhận thấy các góc A, góc B, góc C, góc D đều bằng , nghĩa là các góc của hình chữ nhật đều bằng nhau và bằng .
3. Sau khi sử dụng thước thẳng hoặc compa ta nhận thấy:
+) AB = CD; BC = AD nghĩa là hai cạnh đối của hình chữ nhật bằng nhau
+) AC = BD, nghĩa là hai đường chéo của hình chữ nhật bằng nhau
Câu 3:
1. Vẽ hình chữ nhật ABCD có một cạnh bằng 5 cm, một cạnh bằng 3 cm theo hướng dẫn sau:
Bước 1. Vẽ đoạn thẳng AB = 5 cm.
Bước 2. Vẽ đường thẳng vuông góc với AB tại A. Trên đường thẳng đó lấy điểm D sao cho AD = 3 cm.
Bước 3. Vẽ đường thẳng vuông góc với AB tại B. Trên đường thẳng đó lấy điểm C sao cho BC = 3 cm.
Bước 4. Nối D với C ta được hình chữ nhật ABCD.
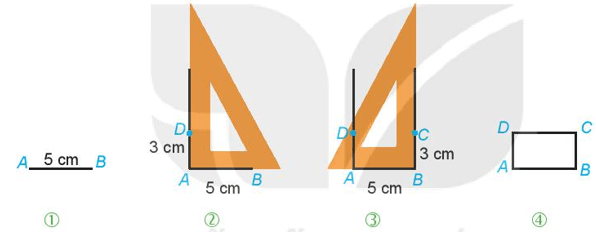
2. Em hãy kiểm tra lại hình vừa vẽ xem các cạnh đối có bằng nhau không? Các góc có bằng nhau không?
 Xem đáp án
Xem đáp án
1. Vẽ hình theo hướng dẫn
2. Kiểm tra lại ta thấy:
+) AB = CD; BC = AD nghĩa là hai cạnh đối của hình chữ nhật bằng nhau.
+) Các góc A, góc B, góc C, góc D đều bằng , nghĩa là các góc của hình chữ nhật đều bằng nhau và bằng .
Câu 4:
1. Trong các đồ vật có ở Hình 4.9, đồ vật nào có dạng hình thoi?

2. Em hãy tìm thêm một số hình ảnh khác của hình thoi trong thực tế.
 Xem đáp án
Xem đáp án
1. Đồ vật có dạng hình thoi là mặt chiếc nhẫn.
2. Một số hình ảnh khác của hình thoi trong thực tế: cánh diều, câu đối trang trí, hoa văn chiếu trúc, hàng rào,…

Câu 5:
Quan sát hình thoi ở Hình 4.10a.
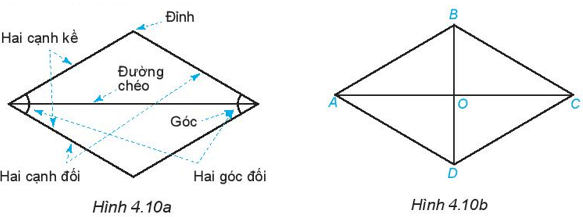
1. Dùng thước thẳng hoặc compa so sánh các cạnh của hình thoi (H.4.10b)
2. Kiểm tra xem hai đường chéo của hình thoi có vuông góc với nhau không?
3. Các cạnh đối của hình thoi có song song với nhau không?
4. Các góc đối của hình thoi ABCD có bằng nhau không?
 Xem đáp án
Xem đáp án
1. Sau khi dùng thước thẳng hoặc compa, ta nhận thấy: AB = BC = CD = AD, nghĩa là các cạnh của hình thoi bằng nhau.
2. Sử dụng eke ta thấy AC vuông góc với BD, nghĩa là hai đường chéo của hình thoi vuông góc với nhau.
3.
+) Khi đặt eke vuông góc với AB ta thấy eke cũng vuông góc với CD. Do đó AB và CD song song với nhau.
+) Khi đặt eke vuông góc với BC ta thấy eke cũng vuông góc với AD. Do đó BC và AD song song với nhau.
Nghĩa là các cạnh đối của hình thoi song song với nhau.
4. Bằng cách gấp giấy, ta thấy các góc đối của hình thoi ABCD bằng nhau.
Câu 6:
Quan sát hình vẽ:
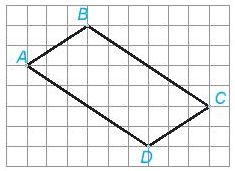
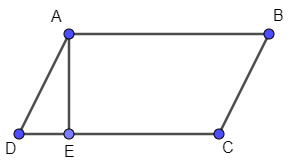
Hãy tìm điểm E trên đoạn thẳng BC, điểm F trên đoạn thẳng AD để tứ giác ABEF là hình thoi.
 Xem đáp án
Xem đáp án
Vì E nằm trên đoạn thẳng BC, điểm F nằm trên đoạn thẳng AD. Để ABEF là hình thoi thì AB = BE = EF = AF.
Ta có thể sử dụng thước thẳng hoặc compa để xác định điểm E và F.
Cách 1: Sử dụng thước thẳng
Bước 1: Đo đoạn thẳng AB
Bước 2:
+) Đo từ B đến đúng khoảng cách bằng đoạn thẳng AB rồi kí hiệu điểm ta được điểm E trên BC.
+) Đo từ A đến đúng khoảng cách bằng đoạn thẳng AB rồi kí hiệu điểm ta được điểm F trên AD.
Cách 2: Sử dụng compa
Bước 1: Đặt compa sao cho tâm compa trùng một trong hai đỉnh A hoặc B, đầu chì trùng với điểm còn lại và giữ nguyên compa
Bước 2:
+) Đặt tâm compa ở điểm B, quay đường tròn cắt BC tại E ta được điểm E.
+) Đặt tâm compa ở điểm A, quay đường tròn cắt AD tại F ta được điểm F.
Từ đó nối các điểm lại với nhau ta được hình thoi ABEF như hình vẽ dưới.
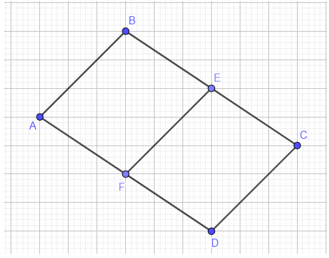
Câu 7:
1. Vẽ hình thoi ABCD có cạnh bằng 3 cm theo hướng dẫn sau:
Bước 1. Vẽ đoạn thẳng AB = 3cm
Bước 2. Vẽ đường thẳng đi qua B. Lấy điểm C trên đường thẳng đó sao cho
BC = 3 cm.
Bước 3. Vẽ đường thẳng đi qua C và song song với cạnh AB. Vẽ đường thẳng đi qua A và song song với cạnh BC.
Bước 4. Hai đường thẳng này cắt nhau tại D, ta được hình thoi ABCD.

2. Em hãy kiểm tra lại hình vừa vẽ xem các cạnh có bằng nhau không?
3. Gấp, cắt hình thoi từ tờ giấy hình chữ nhật theo hướng dẫn sau:
Bước 1. Gấp đôi tờ giấy, sau đó lại gấp đôi một lần nữa sao cho xuất hiện một góc vuông với cạnh là các nếp gấp.
Bước 2. Vẽ một đoạn thẳng nối hai điểm tùy ý trên hai cạnh của góc vuông.
Bước 3. Dùng kéo cắt theo đoạn thẳng vừa vẽ ròi mở ra, ta được một hình thoi.

 Xem đáp án
Xem đáp án
1. Vẽ hình theo hướng dẫn
2. Sau khi vẽ xong hình, sử dụng thước thẳng ta nhận thấy: AB = BC = CD = AD = 3cm
Nghĩa là các cạnh có bằng nhau.
3. Gấp, cắt hình thoi theo hướng dẫn.
Câu 8:
Em hãy vẽ đường trang trí theo mẫu dưới đây rồi tô màu tùy ý
 Xem đáp án
Xem đáp án
Học sinh thoải mái ý tưởng để vẽ hình
Dưới đây là một hình minh họa

Câu 9:
1. Hình bình hành có trong hình ảnh nào dưới đây (H.4.11)?

2. Em hãy tìm thêm một số hình ảnh khác của hình bình hành trong thực tế.
 Xem đáp án
Xem đáp án
1. Hình hình hành có ở hình c.
2. Một số hình ảnh khác của hình bình hành trong thực tế: mái nhà, cầu thang, …

Câu 10:
Quan sát hình bình hành ở Hình 4.12a.
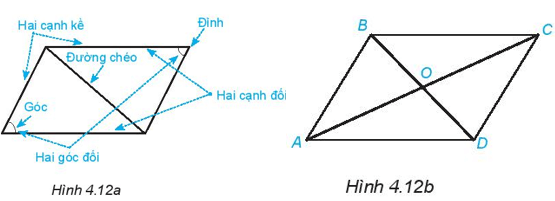
1. Đo và so sánh độ dài các cạnh đối của hình bình hành ABCD (H.4.12b)
2. Đo và so sánh OA với OC, OB với OD.
3. Các cạnh đối của hình hình hành ABCD có song song với nhau không?
4. Các góc đối của hình bình hành ABCD có bằng nhau không?
 Xem đáp án
Xem đáp án
1. Sau khi sử dụng thước thẳng để đo đoạn thẳng, ta nhận thấy: AB = CD; BC = AD, nghĩa là các cạnh đối của hình bình hành bằng nhau.
2. Sau khi sử dụng thước thẳng để đo đoạn thẳng, ta nhận thấy: OA = OC; OB = OD
3.
+) Khi đặt eke vuông góc với AB ta thấy eke cũng vuông góc với CD. Do đó AB và CD song song với nhau.
+) Khi đặt eke vuông góc với BC ta thấy eke cũng vuông góc với AD. Do đó BC và AD song song với nhau.
Nghĩa là các cạnh đối của hình bình hành song song với nhau.
4. Bằng cách gấp giấy, ta thấy các góc đối của hình bình hành bằng nhau.
Câu 11:
Vẽ hình bình hành ABCD có AB = 5 cm; BC = 3 cm theo hướng dẫn sau:
Bước 1. Vẽ đoạn thẳng AB = 5 cm.
Bước 2. Vẽ đường thẳng đi qua B. Trên đường thẳng đó lấy điểm C sao cho
BC = 3 cm.
Bước 3. Vẽ đường thẳng đi qua A và song song với BC, đường thẳng qua C và song song với AB. Hai đường thẳng này cắt nhau tại D, ta được hình bình hành ABCD.
 Xem đáp án
Xem đáp án
Vẽ hình theo hướng dẫn trên.
Câu 12:
Mặt bàn ở hình bên là hình ảnh của một hình thang cân. Em hãy tìm thêm một số hình ảnh khác của hình thang cân trong thực tế.

 Xem đáp án
Xem đáp án
Một số hình ảnh khác của hình thang cân trong thực tế: cái thang, mặt túi xách, túi đựng bỏng ngô, …

Câu 13:
Quan sát hình thang cân ở Hình 4.13a.
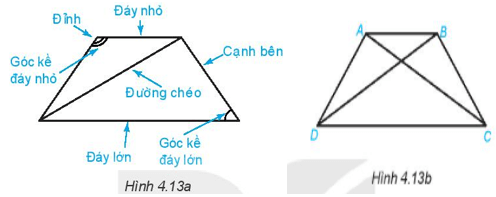
1. Gọi tên các đỉnh, đáy lớn, đáy nhỏ, đường chéo, cạnh bên của hình thang cân ABCD (H.4.13b).
2. Sử dụng thước thẳng hoặc compa để so sánh hai cạnh bên, hai đường chéo của hình thang cân ABCD.
3. Hai đáy của hình thang cân ABCD có song song với nhau không?
4. Hai góc kề một đáy của hình thang cân ABCD có bằng nhau không?
 Xem đáp án
Xem đáp án
1. Trong hình thang cân ABCD:
+) Đỉnh: A, B, C, D
+) Đáy lớn: DC
+) Đáy nhỏ: AB
+) Đường chéo: AC, BD
+) Cạnh bên: AD, BC
2. Sau khi sử dụng thước thẳng hoặc compa để đo ta nhận thấy: AD = BC; AC = BD, nghĩa là hai cạnh bên hình thang cân bằng nhau, hai đường chéo hình thang cân bằng nhau
3. Khi đặt eke vuông góc với AB ta thấy eke cũng vuông góc với CD. Do đó AB và CD song song với nhau.
Nghĩa là hai đáy của hình bình hành song song với nhau.
4. Bằng cách gấp giấy ta thấy hai góc kề một đáy của hình thang bằng nhau
Câu 14:
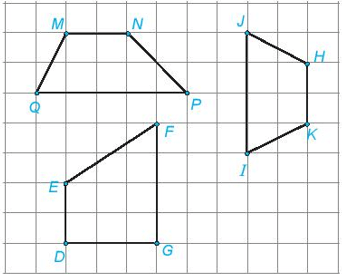
Hình nào trong các hình đã cho là hình thang cân? Hãy cho biết tên hình thang cân đó
 Xem đáp án
Xem đáp án
Hình thang cân trong các hình là hình thang HKIJ vì có HJ = KI.
Câu 15:
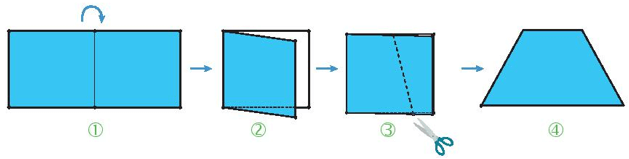
Gấp, cắt hình thang cân từ tờ giấy hình chữ nhật.
Bước 1. Gấp đôi tờ giấy
Bước 2. Vẽ một đoạn thẳng nối hai điểm tùy ý trên hai cạnh đối diện (cạnh không chứa nếp gấp)
Bước 3. Cắt theo đường vừa vẽ.
Bước 4. Mở tờ giấy ra ta được một hình thang cân.
 Xem đáp án
Xem đáp án
Cắt, gấp như hình vẽ trên.
Câu 16:
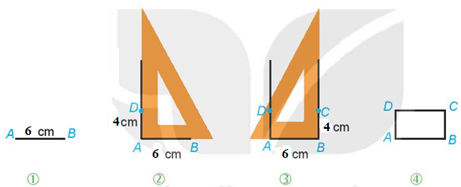
Vẽ hình chữ nhật có một cạnh dài 6 cm, một cạnh dài 4 cm.
 Xem đáp án
Xem đáp án
Vẽ hình chữ nhật ABCD có một cạnh bằng 6 cm, một cạnh bằng 4 cm theo hướng dẫn sau:
Bước 1. Vẽ đoạn thẳng AB = 6 cm.
Bước 2. Vẽ đường thẳng vuông góc với AB tại A. Trên đường thẳng đó lấy điểm D sao cho AD = 4 cm.
Bước 3. Vẽ đường thẳng vuông góc với AB tại B. Trên đường thẳng đó lấy điểm C sao cho BC = 4 cm.
Bước 4. Nối D với C ta được hình chữ nhật ABCD.
Câu 17:
Vẽ hình thoi có cạnh 4 cm.
 Xem đáp án
Xem đáp án
Vẽ hình thoi ABCD có cạnh bằng 4 cm theo hướng dẫn sau:
Bước 1. Vẽ đoạn thẳng AB = 4cm
Bước 2. Vẽ đường thẳng đi qua B. Lấy điểm C trên đường thẳng đó sao cho
BC = 4 cm.
Bước 3. Vẽ đường thẳng đi qua C và song song với cạnh AB. Vẽ đường thẳng đi qua A và song song với cạnh BC.
Bước 4. Hai đường thẳng này cắt nhau tại D, ta được hình thoi ABCD.
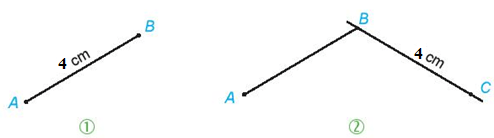
Câu 18:
Vẽ hình bình hành có độ dài một cạnh bằng 6 cm, một cạnh bằng 3 cm.
 Xem đáp án
Xem đáp án
Vẽ hình bình hành ABCD có AB = 6 cm; BC = 3 cm theo hướng dẫn sau:
Bước 1. Vẽ đoạn thẳng AB = 6 cm.
Bước 2. Vẽ đường thẳng đi qua B. Trên đường thẳng đó lấy điểm C sao cho
BC = 3 cm.
Bước 3. Vẽ đường thẳng đi qua A và song song với BC, đường thẳng qua C và song song với AB. Hai đường thẳng này cắt nhau tại D, ta được hình bình hành ABCD.
Câu 19:
Hãy kể tên các hình thang cân, hình chữ nhật có trong hình lục giác đều sau:
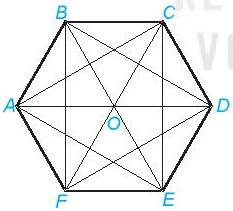
 Xem đáp án
Xem đáp án
+) Các hình thang cân: ABCD, BCDE, CDEF, DEFA, EFAB, FABC
+) Các hình chữ nhật: ABDE, BCEF, CDFA.
Câu 20:
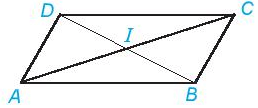
Cho hình bình hành ABCD, hai đường chéo AC và BD cắt nhau tại điểm I. Sử dụng compa hoặc thước thẳng kiểm tra xem điểm I có là trung điểm của hai đường chéo AC và BD không?
 Xem đáp án
Xem đáp án
Sử dụng thước thẳng đo đoạn thẳng hoặc compa ta nhận thấy ID = IB; IC = IA
Do đó I là trung điểm của hai đường chéo AC và BD.
Câu 21:
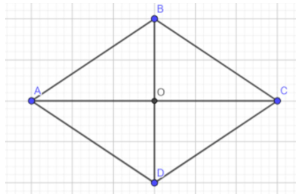
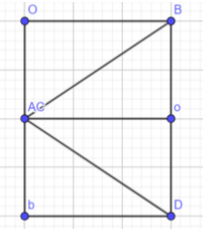
Vẽ và cắt từ giấy một hình thoi tùy ý. Sau đó cắt hình thoi theo hai đường chéo của nó để được bốn mảnh. Ghép lại bốn mảnh đó để được một hình chữ nhật.
 Xem đáp án
Xem đáp án
+) Cắt tờ giấy hình thoi thành 4 mảnh được minh họa:
+) Sau đó ghép lại để được hình chữ nhật như sau:
Câu 22:
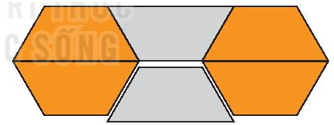
“Bàn làm việc đa năng”. Hãy cắt 6 hình thang cân giống nhau rồi ghép thành hình mặt chiếc bàn làm việc như hình dưới đây.
 Xem đáp án
Xem đáp án
Cắt 6 hình thang giống hết nhau rồi ghép lại như hình vẽ
Câu 23:
Lấy ví dụ về các hình có dạng hình chữ nhật trong thực tiễn.
 Xem đáp án
Xem đáp án
Mặt bàn, Mặt bảng, cửa ra vào, cửa sổ, …
Câu 24:
Vẽ hình thoi cạnh 4cm.
 Xem đáp án
Xem đáp án
Bước 1. Vẽ đoạn thẳng AB = 4cm.
Bước 2. Vẽ đoạn thẳng BC = 4cm (điểm C khác điểm A).
Bước 3. Qua điểm C vẽ đường thẳng song song với AB. Trên đường thẳng này lấy điểm D sao cho CD = 4cm.
Bước 4. Nối D với A ta được hình thoi ABCD.
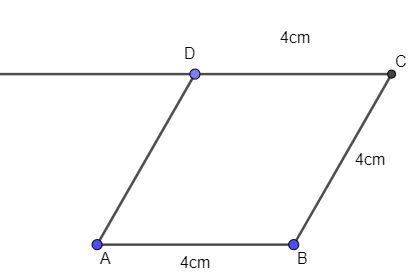
Câu 25:
Cho hình bình hành ABCD, hai đường chéo AC và BD cắt nhau tại điểm I. Sử dụng compa hoặc thước thẳng kiểm tra xem điểm I có là trung điểm của hai đường chéo không?
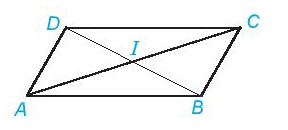
 Xem đáp án
Xem đáp án
+) Nếu sử dụng compa:
- Đầu tiên mở một khoảng compa trùng với đoạn IA. Sau đó giữ nguyên khoảng đó đặt vào đoạn IC thấy trùng nhau.
- Tương tự mở compa một khoảng trùng với IB. Sau đó giữ nguyên khoảng đó đặt vào đoạn ID thấy trùng nhau.
Vậy điểm I chính là trung điểm của hai đường chéo.
+) Nếu sử dụng thước thẳng:
Ta sẽ đo độ dài của từng đoạn một, thì thấy IA = IC, IB = IB.
Vậy I chính là trung điểm của hai đường chéo.
Câu 26:
Hình nào trong các hình đã cho là hình thang cân? Hãy cho biết tên hình thang cân đó.
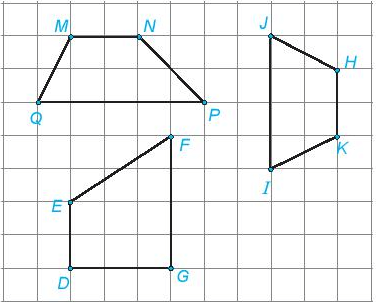
 Xem đáp án
Xem đáp án
Đầu tiên lấy eke kiểm tra hai cạnh đáy có song song với nhau không.
Tiếp theo lấy thước thẳng đo độ dài hai đường chéo nếu bằng nhau thì là hình thang cân.
Từ kết quả đo, ta thấy các hình trên hình thang cân là HKIJ.
Câu 27:
Hãy kể tên các hình thang cân, hình chữ nhật, hình thoi có trong lục giác đều sau:
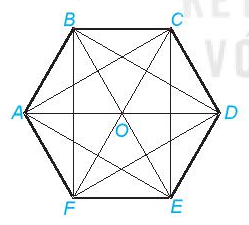
 Xem đáp án
Xem đáp án
Trong hình đã cho:
- Hình thang cân: ABCD, BCDE, DEFA, EFAB.
- Hình chữ nhật: ACDF, BCEF.
- Hình thoi: ABOF, ABCO, BCDO, DEFO, CDEO, EFAO.
Câu 28:
Vẽ hình chữ nhật có một cạnh dài 7cm, một cạnh 3cm.
 Xem đáp án
Xem đáp án
Bước 1. Vẽ đoạn thẳng AB = 7cm.
Bước 2. Dựng đường thẳng vuông góc với AB tại A. Trên đường thẳng này lấy điểm D sao cho AD = 3cm.
Bước 3. Dựng đường thẳng vuông góc với AB tại B. Trên đường thẳng này lấy điểm C sao cho BC = 3cm.
Bước 4. Nối C với D ta được hình chữ nhật có AB = 7cm, AD = 3cm.
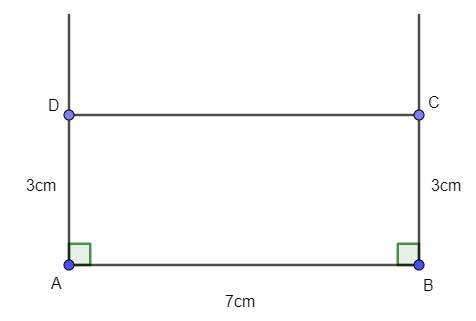
Câu 29:
Quan sát hình sau và cho biết hình nào là hình chữ nhật, hình nào là hình thoi?
 Xem đáp án
Xem đáp án
Đáp án C
Không có hình thoi và hình chữ nhật là Hình a).
Câu 30:
Trong các hình sau đây, hình nào là hình chữ nhật?

 Xem đáp án
Xem đáp án
Đáp án D
Hình a) màn hình tivi là hình chữ nhật.
Hình b) là chiếc cửa có dạng hình chữ nhật.
Hình c) là các khung ảnh cũng có dạng hình chữ nhật.
Câu 32:
Có bao nhiêu tính chất dưới đây là tính chất của hình thang cân?
a) Trong hình thang cân có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.
b) Trong hình thang cân có hai đường chéo bằng nhau.
c) Trong hình thang cân có hai góc kề một đáy bằng nhau.
d) Trong hình thang cân có hai cặp cạnh đối song song với nhau.
 Xem đáp án
Xem đáp án
Đáp án B
Trong hình thang cân:
- Hai cạnh bên bằng nhau.
- Hai đường chéo bằng nhau.
- Hai góc kề một đáy bằng nhau.
- Hai cạnh đáy song song với nhau.
Do đó a), d) sai còn b) và c) đúng.
Vậy có hai tính chất đúng.
Câu 33:
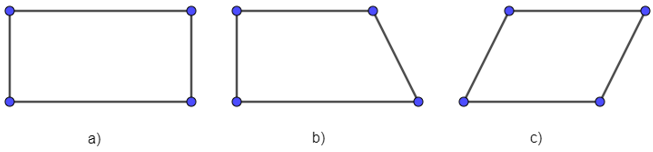
Hình nào dưới đây là hình bình hành?
 Xem đáp án
Xem đáp án
Đáp án B
Trong các hình đã cho, hình 2 là hình bình hành.
Câu 34:
Cho hình chữ nhật MNPQ, ta có:
 Xem đáp án
Xem đáp án
Đáp án D
Hình chữ nhật MNPQ có các cạnh đối bằng nhau, hai đường chéo bằng nhau nên MN = PQ, MP = NQ.
Đo đó D đúng.
Câu 36:
Quan sát hình bên. Mặt bàn này hình gì?

 Xem đáp án
Xem đáp án
Đáp án D
Quan sát vào hình ảnh ta thấy đây là một chiếc bàn có mặt bàn là hình thang cân.
Câu 37:
Cái kim trên la bàn có dạng hình gì?

 Xem đáp án
Xem đáp án
Đáp án A
Chiếc kim trên mặt la bàn có dạng hình thoi.
Câu 38:
Phát biểu nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án B
Trong hình bình hành không có hai đường chéo bằng nhau nên hình bình hành không phải hình thang cân. Do đó A sai, D sai.
Trong hình chữ nhật có hai cạnh đáy song song với nhau, có hai góc kề một đáy bằng nhau, hai cạnh bên bằng nhau và hai đường chéo bằng nhau nên hình chữ nhật là hình thang cân. Do đó B đúng.
Trong hình thoi không có hai đường chéo bằng nhau nên hình thoi không phải hình thang cân. Do đó C sai.
Câu 39:
Cho hình chữ nhật ABCD có AB = 5cm, BC = 2cm thì:
 Xem đáp án
Xem đáp án
Đáp án A
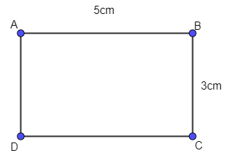
Vì ABCD là hình chữ nhật nên AB = CD = 5cm.
Câu 40:
Các bước vẽ hình bình hành DEFG có DE = 4cm; EF = 3cm như sau:
Bước 1. Vẽ đoạn DE = 3cm.
Bước 2. Vẽ đường thẳng đi qua E. Trên đường thẳng này lấy điểm F sao cho EF = 3cm.
Bước 3. Vẽ đường thẳng đi qua D và song song với EF. Trên đường thẳng này lấy điểm G sao cho DG = EF = 3cm.
Bước 4. Nối điểm G với điểm F lại ta được hình bình hành DEFG.
Trong các bước vẽ trên có bao nhiêu bước làm đúng?
 Xem đáp án
Xem đáp án
Đáp án A
Các bước vẽ hình bình hành DEFG có DE = 4cm; EF = 3cm như sau:
Bước 1. Vẽ đoạn DE = 5cm.
Bước 2. Vẽ đường thẳng đi qua E. Trên đường thẳng này lấy điểm F sao cho EF = 3cm.
Bước 3. Vẽ đường thẳng đi qua D và song song với EF. Trên đường thẳng này lấy điểm G sao cho DG = EF = 3cm.
Bước 4. Nối điểm G với điểm F lại ta được hình bình hành DEFG.
Có bước 1 sai vì đoạn DE = 5cm.
Câu 41:
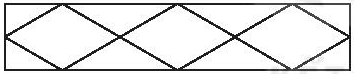
Trong hình sau có bao nhiêu hình thoi?
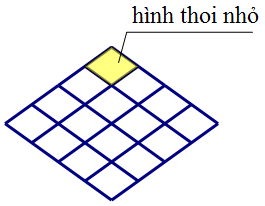
 Xem đáp án
Xem đáp án
Đáp án D
Có 16 hình thoi nhỏ.
Có 9 hình thoi vừa.
Có 1 hình thoi to.
Tổng có 16 + 9 + 1 = 26 hình thoi.