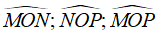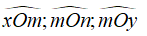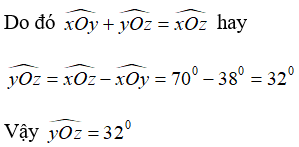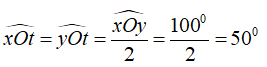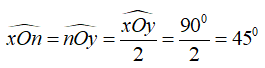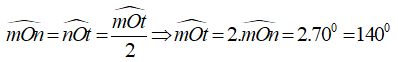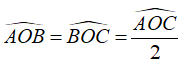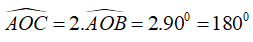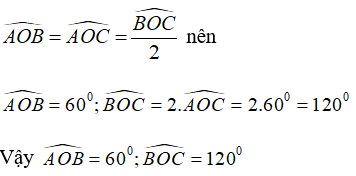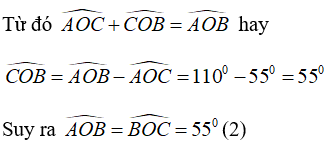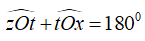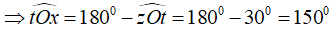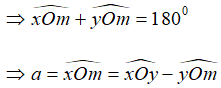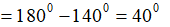Tổng hợp bài tập Chương 2 phần Hình học Toán 6 có đáp án
-
2094 lượt thi
-
40 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Chọn câu sai:
 Xem đáp án
Xem đáp án
Đáp án là B
Ta có:
+ Góc là hình gồm hai tia chung gốc nên A đúng.
+ Góc bẹt là góc có hai cạnh là hai tia đối nhau nên B sai vì hai tia chung gốc chưa chắc đã đối nhau.
+ Hai góc bằng nhau có số đo bằng nhau nên C đúng.
+ Hai góc có số đo bằng nhau thì bằng nhau nên D đúng.
Câu 2:
Chọn câu sai:
 Xem đáp án
Xem đáp án
Đáp án là D
Ta có góc vuông là góc có số đo bằng ; góc có số đo lớn hơn 0° và nhỏ hơn là góc nhọn và góc tù là góc có số đo lớn hơn và nhỏ hơn nên A, B, C đều đúng.
Góc có số đo nhỏ hơn là góc tù là sai vì góc nhọn, góc vuông đều có số đo nhỏ hơn
Câu 3:
Chọn phát biểu đúng:
 Xem đáp án
Xem đáp án
Đáp án là D
+ Góc có số đo là góc tù vì < < nên A sai.
+ Góc có số đo là góc nhọn vì 0° < < nên B sai.
+ Góc có số đo là góc tù vì < < nên C sai.
+ Góc có số đo là góc tù vì < < nên D đúng.
Câu 4:
Cho 9 tia chung gốc (không có tia nào trùng nhau) thì số góc tạo thành là:
 Xem đáp án
Xem đáp án
Đáp án là C
Số góc tạo thành là 9.(9 - 1)/2 = 36 góc
Câu 6:
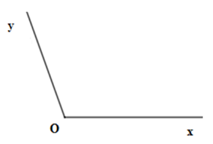
Cho hình vẽ sau:
Chọn câu đúng:
 Xem đáp án
Xem đáp án
Đáp án là A
Góc trên hình là ∠xOy, đỉnh O, cạnh Ox và Oy.
Câu 8:
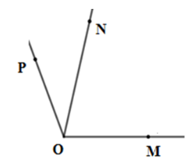
Kể tên tất cả các góc có một cạnh là Om có trên hình vẽ sau:
 Xem đáp án
Xem đáp án
Đáp án là D
Các góc cần tìm là:
Câu 9:
Cho ∠xOm = và góc xOm bằng góc yAn. Khi đó góc yAn bằng:
 Xem đáp án
Xem đáp án
Đáp án là C
Vì ∠xOm = ∠yAn mà ∠xOm = nên ∠yAn =
Câu 10:
Cho các góc sau: ∠A = ; ∠B = ; ∠C = ; ∠D = . Chọn câu sai:
 Xem đáp án
Xem đáp án
Đáp án là B
Ta có:
+ ∠B < ∠D ( < ) nên A đúng.
+ ∠C > ∠D ( > ) nên B sai.
+ ∠A < ∠B ( < ) nên C đúng.
+ ∠B < ∠C (< ) nên D đúng.
Câu 11:
Chọn phát biểu đúng trong các phát biểu sau:
 Xem đáp án
Xem đáp án
Đáp án là C
+ Nếu tia Oy nằm giữa hai tia On và Om thì khi đó ta có: ∠yOn + ∠yOm = ∠mOn nên C đúng.
+ Nếu ∠A và ∠B là hai góc bù nhau thì ∠A + ∠B = nên D sai.
+ Hai góc kề nhau là hai góc có một cạnh chung và hai cạnh còn lại nằm trên hai nửa mặt phẳng đối nhau có bờ là đường thẳng chứa cạnh chung nên hai góc tù chưa chắc kề nhau, suy ra A sai.
+ Cho ba tia chung gốc Ox, Oy, Oz, ta luôn có: ∠xOy + ∠yOz = ∠xOz là sai vì thiếu điều kiện Oy nằm giữa Ox và Oz. Suy ra B sai.
Câu 12:
Chọn câu sai trong các câu sau:
 Xem đáp án
Xem đáp án
Đáp án là C
Các đáp án A, B, D đúng.
C sai vì hai góc vừa kề nhau, vừa bù nhau là hai góc kề bù.
Câu 13:
Trên cùng một nửa mặt phẳng bờ là tia Ox có ∠xOy = 30°, ∠xOz = 65°, chọn phát biểu đúng trong các phát biểu sau:
 Xem đáp án
Xem đáp án
Đáp án là B
Vì ∠xOy = , ∠xOz = , suy ra ∠xOy < ∠xOz ( < ) nên tia Oy nằm giữa hai tia Oz và Ox
Câu 14:
Cho ∠xOy và ∠yOy' là hai góc kề bù. Biết ∠xOy = , số đo của ∠yOy' là:
 Xem đáp án
Xem đáp án
Đáp án là A
Vì ∠xOy và ∠yOy' là hai góc kề bù nên ta có: ∠xOy + ∠yOy' = ⇒ ∠yOy' = - =
Câu 15:
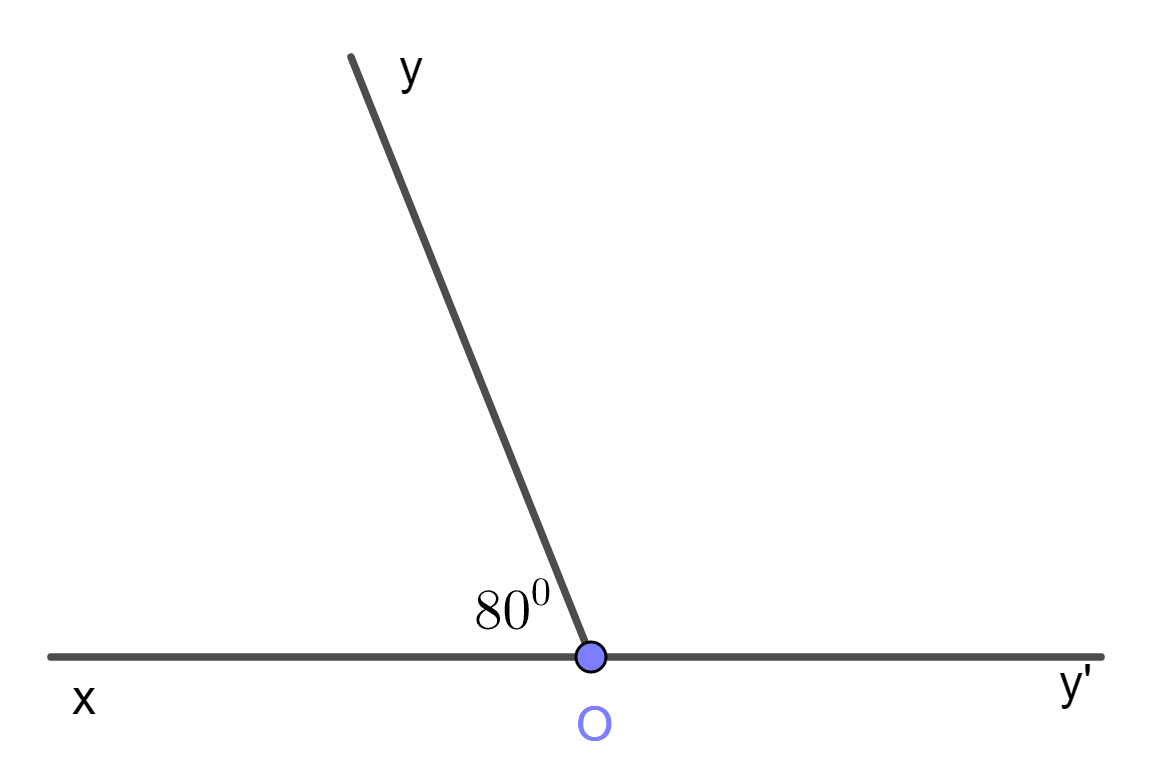
Cho hình vẽ:
Số đo của ∠tOm là:
 Xem đáp án
Xem đáp án
Đáp án là D
Vì tia On nằm giữa hai tia Om và Ot ⇒ ∠tOn + ∠nOm = ∠tOm ⇒ ∠tOm =
Câu 16:
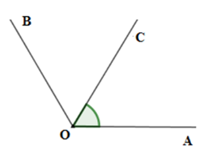
Cho ∠AOB = , vẽ tia OC sao cho tia OB nằm giữa hai tia OA và OC đồng thời ∠COB = . Tính số đo ∠AOC
 Xem đáp án
Xem đáp án
Đáp án là B
Vì tia OB nằm giữa hai tia OA và OC nên ∠AOB + ∠BOC = ∠AOC
Suy ra ∠AOC =
Câu 17:
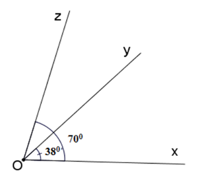
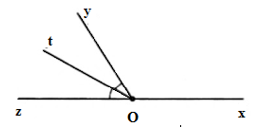
Tính góc yOz trong hình vẽ sau:
 Xem đáp án
Xem đáp án
Đáp án là A
Vì hai tia Oy, Oz cùng thuộc nửa mặt phẳng bờ là đường thẳng chứa tia Ox
Lại có ∠xOy < ∠xOz ( <) nên tia Oy nằm giữa hai tia Ox và Oz
Câu 18:
Cho ∠A và ∠B là hai góc phụ nhau và chúng có số đo bằng nhau. Tính số đo mỗi góc:
 Xem đáp án
Xem đáp án
Đáp án là C
Vì ∠A và ∠B là hai góc phụ nhau nên ∠A + ∠B = mà ∠A = ∠B
Nên ta có ∠A + ∠A = hay 2.∠A = suy ra ∠B = ∠A = : 2 =
Câu 19:
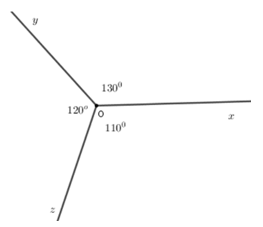
Cho ba tia chung gốc Ox; Oy; Oz thỏa mãn ∠xOy = ; ∠yOz = ; ∠zOx = . Chọn câu đúng:
 Xem đáp án
Xem đáp án
Đáp án là C
Ta có ∠xOy + ∠yOz > ∠xOz (do + > ) nên tia Oy không nằm giữa hai tia Oz và Ox
Lại có ∠xOy + ∠xOz > ∠yOz (do + > ) nên tia Ox không nằm giữa hai tia Oy và Oz
Lại có ∠zOy + ∠xOz > ∠xOy (do + > ) nên tia Oz không nằm giữa hai tia Oy và Ox
Vậy không có tia nào nằm giữa hai tia còn lại.
Câu 20:
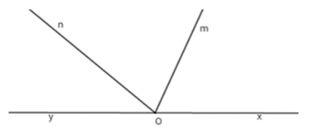
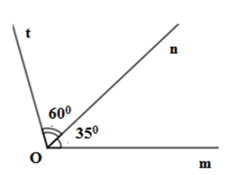
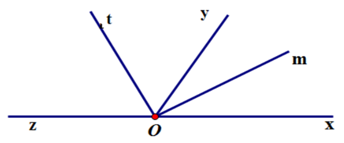
Cho hình vẽ sau với và là hai tia đối nhau. Chọn câu sai:
 Xem đáp án
Xem đáp án
Đáp án là B
+ Hai góc ∠mOx; ∠mOz là hai góc kề bù nên A đúng.
+ Hai góc ∠xOy; ∠tOz là hai góc không kề nhau nên B sai.
+ Hai góc ∠tOy; ∠yOx là hai góc kề nhau nên C đúng.
+ Hai góc ∠tOz; ∠tOx là hai góc kề bù nên D đúng.
Câu 21:
Chọn phát biểu sai trong các phát biểu sau:
 Xem đáp án
Xem đáp án
Đáp án là C
Nếu ∠xOt = ∠yOt và tia Ot nằm giữa hai tia Ox, Oy thì tia Ot là tia phân giác của ∠xOy nên C sai, D đúng
Câu 22:
Cho Ot là phân giác của ∠xOy. Biết ∠xOy = 100°, số đo của ∠xOt là:
 Xem đáp án
Xem đáp án
Đáp án là C
Vì Ot là phân giác của ∠xOy thì
Câu 23:
Cho ∠xOy là góc vuông có tia On là phân giác, số đo của ∠xOn là:
 Xem đáp án
Xem đáp án
Đáp án là C
Vì On là tia phân giác của ∠xOy nên
Câu 24:
Cho tia On là tia phân giác của ∠mOt. Biết ∠mOn =, số đo của ∠mOt là:
 Xem đáp án
Xem đáp án
Đáp án là A
Vì tia On là tia phân giác của ∠mOt nên
Câu 25:
Cho ∠AOB = và tia OB là tia phân giác của góc AOC . Khi đó góc AOC là:
 Xem đáp án
Xem đáp án
Đáp án là D
Vì tia là tia phân giác của góc nên
Do đó
Nên góc AOC là góc bẹt.
Câu 26:
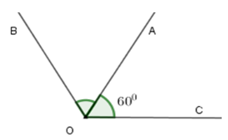
Cho ∠AOC = . Vẽ tia OB sao cho OA là tia phân giác của ∠BOC . Tính số đo của ∠AOB và ∠BOC
 Xem đáp án
Xem đáp án
Đáp án là D
Vì OA là tia phân giác của ∠BOC nên ta có:
Câu 27:
Cho ∠AOB = và ∠AOC = sao cho ∠AOB và ∠AOC không kề nhau. Chọn câu sai:
 Xem đáp án
Xem đáp án
Đáp án là C
Vì ∠AOB và ∠AOC không kề nhau nên hai tia OC; OB thuộc cùng nửa mặt phẳng bở là đường thẳng chứa tia OA.
Lại có: ∠AOC < ∠AOB (55° < 110°) nên tia OC nằm giữa hai tia OA và OB . (1)
Từ (1) và (2) suy ra tia OC là tia phân giác góc AOB.
Vậy A, B, D đúng và C sai.
Câu 28:
Cho ∠xOy và ∠yOz là hai góc kề bù. Biết ∠xOy = và tia Ot là tia phân giác của ∠yOz. Tính số đo góc xOt.
 Xem đáp án
Xem đáp án
Đáp án là B
Vì ∠xOy và ∠yOz là hai góc kề bù nên ∠xOy + ∠yOz = mà ∠xOy = nên ∠yOz = - =
Lại có tia Ot là tia phân giác của ∠yOz nên
Lại có ∠zOt; ∠tOx là hai góc kề bù nên
Vậy ∠tOx =
Câu 29:
Cho góc AOB và tia phân giác OC của góc đó. Vẽ tia phân giác OM của góc BOC . Biết ∠BOM = . Tính số đo góc AOB
 Xem đáp án
Xem đáp án
Đáp án là C
Vì tia OM là tia phân giác góc BOC nên ∠BOC = 2.∠BOM = 2. =
Lại có tia Oc là tia phân giác góc AOB nên ∠AOB = 2.∠BOC = 2. =
Vậy ∠AOB =
Câu 30:
Cho góc bẹt ∠xOy. Trên cùng một nửa mặt phẳng bờ xy vẽ các tia Om, On sao cho ∠xOm = (a < 180) và ∠yOn = . Với giá trị nào a của thì tia On là tia phân giác của ∠yOm
 Xem đáp án
Xem đáp án
Đáp án là D
Vì tia On là tia phân giác của ∠yOm nên ∠yOm = 2.∠yOn = 2. =
Lại có xOy là góc bẹt nên ∠xOm và ∠yOm là hai góc kề bù
Vậy a =
Câu 31:
Chọn phát biểu đúng trong các phát biểu sau:
 Xem đáp án
Xem đáp án
Đáp án là A
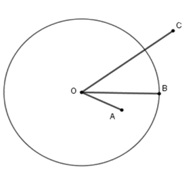
Đường tròn tâm O, bán kính R là hình gồm các điểm cách O một khoảng bằng R , kí hiệu là (O; R) nên A đúng, C sai.
Đường tròn tâm O đường kính R có bán kính R/2 nên là tập hợp các điểm cách O một khoảng R/2 . Đáp án B sai
Hình tròn là hình gồm các điểm nằm trên đường tròn và các điểm nằm bên trong đường tròn đó. Đáp án D sai
Câu 32:
Chọn phát biểu sai trong các phát biểu sau:
 Xem đáp án
Xem đáp án
Đáp án là B
Ta thấy A, C, D đúng.
B sai vì dây cung không thể là bán kính của đường tròn (theo định nghĩa dây cung)
Câu 33:
Nếu điểm M nằm trong đường tròn tâm O bán kính 4cm. Khi đó:
 Xem đáp án
Xem đáp án
Đáp án là A
Vì điểm M nằm trong đường tròn tâm O bán kính 4cm nên OM < 4cm.
Câu 34:
Cho đường tròn (O; 5cm) và OM = 6cm. Chọn câu đúng:
 Xem đáp án
Xem đáp án
Đáp án là C
Ta thấy OM > R (6cm > 5cm) nên điểm M nằm ngoài đường tròn (O; R)
Câu 35:
Cho đường tròn (M; 1,5cm) và ba điểm A, B, C sao cho OA = 1cm; OB = 1,5cm; OC = 2cm. Chọn câu đúng:
 Xem đáp án
Xem đáp án
Đáp án là C
Đường tròn (M; 1,5cm) có tâm M và bán kính R = 1,5cm
Ta thấy:
+ OA < R (1cm < 1,5cm) nên điểm A nằm trong đường tròn (M; 1,5cm)
+ OB = R (1,5cm = 1,5cm) nên điểm B nằm trên (thuộc) đường tròn (M; 1,5cm)
+ OC > R (2cm > 1,5cm) nên điểm C nằm ngoài đường tròn (M; 1,5cm)
Câu 36:
Cho hình vẽ sau:
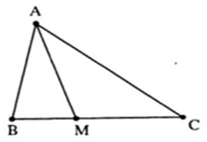
Kể tên các góc trong tam giác ABM:
 Xem đáp án
Xem đáp án
Đáp án là A
Các góc trong tam giác ABM là:
Câu 37:
Cho hình vẽ sau:
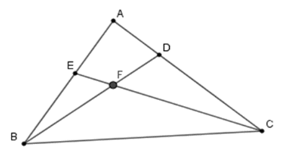
Kể tên các tam giác có chung cạnh BC:
 Xem đáp án
Xem đáp án
Đáp án là D
Các tam giác có chung cạnh trong hình vẽ là: ΔFBC; ΔEBC; ΔDBC; ΔABC
Câu 38:
Cho hình vẽ sau:
Có bao nhiêu cặp tam giác mà có một góc của tam giác này kề bù với một góc của tam giác kia:
 Xem đáp án
Xem đáp án
Đáp án là C
Ta thấy trên hình vẽ có các cặp góc kề bù mà mỗi góc thuộc một tam giác là: ∠EFB và ∠CFB; ∠BFC và ∠CFD; ∠BEC và ∠AEC; ∠BDC và ∠BDA
Như vậy ta có bốn cặp tam giác thỏa mãn điểu kiện là: ΔBEF và ΔBFC; ΔDFC và ΔBFC; ΔBEC và ΔAEC; ΔBDC và ΔBDA
Câu 39:
Cho hình vẽ dưới đây:
Góc AEB là góc chung của những tam giác nào:
 Xem đáp án
Xem đáp án
Đáp án là B
Ta có các tam giác có chứa góc AEB là: ΔAEB; ΔAED
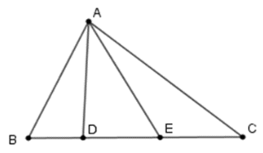
Câu 40:
Cho hình vẽ dưới đây:
Có bao nhiêu tam giác có một cạnh AD trên hình vẽ:
 Xem đáp án
Xem đáp án
Đáp án là D
Các tam giác có một cạnh AD trên hình vẽ là: ABD; ADE; ADC