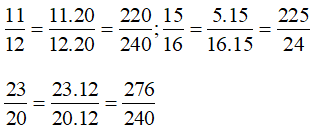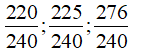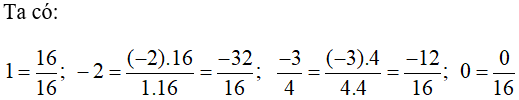22 câu hỏi trắc nghiệm thuộc Bài tập: Quy đồng mẫu nhiều phân số chọn lọc, có đáp án

Câu 1:

Mẫu số chung của các phân số $\frac{2}{5}; \frac{23}{18}; \frac{5}{75}$ là:

A. 180

B. 500

C. 750

D. 450

Xem đáp án

Đáp án là D

Ta có:

5 = 5.1

18 = 2. $3^{2}$

75 = 3. $5^{2}$

⇒ BCNN(5; 18; 75) = 2. $3^{2}$ . $5^{2}$ = 450

Vậy ta có thể chọn một mẫu chung là 450

Câu 2:

Qui đồng mẫu các phân số $\frac{11}{12}; \frac{15}{16}; \frac{23}{20}$ ta được các phân số lần lượt là

A. $\frac{220}{240}; \frac{225}{240}; \frac{276}{240}$

B. $\frac{225}{240}; \frac{220}{240}; \frac{276}{240}$

C. $\frac{225}{240}; \frac{276}{240}; \frac{220}{240}$

D. $\frac{220}{240}; \frac{276}{240}; \frac{225}{240}$

Xem đáp án

Đáp án là A

Ta có 12 = $2^{2}$ .3; 16 = $2^{4}$ ; 20 = $2^{2}$ .5 ⇒ MC = BCNN(12; 16; 20) = $2^{4}$ .3.5 = 240

Vậy các phân số sau khi được quy đồng lần lượt là

Câu 3:

Quy đồng mẫu số hai phân số $\frac{2}{7}; \frac{5}{- 8}$ được hai phân số lần lượt là :

A. $\frac{16}{56}; \frac{- 35}{56}$

B. $\frac{16}{56}; \frac{35}{56}$

C. $\frac{16}{56}; \frac{35}{- 56}$

D. $\frac{- 16}{56}; \frac{- 35}{56}$

Xem đáp án

Đáp án là A

Câu 4:

Mẫu chung nguyên dương nhỏ nhất của các phân số $\frac{19}{3^{2} . 7.11}; \frac{23}{3^{3} . 7^{2} . 19}$ là :

A. $3^{2}$ . $7^{2}$

B. $3^{3}$ . $7^{3}$ .11.19

C. $3^{2}$ . $7^{2}$ .11.19

D. $3^{3}$ . $7^{2}$ .11.19

Xem đáp án

Đáp án là D

BCNN hay mẫu số chung nguyên dương nhỏ nhất của hai mẫu đã cho là $3^{3} . 7^{2} . 11.19$

Câu 5:

Cho các phân số $\frac{5}{28}$ và $\frac{9}{50}$ . Trong các khẳng định sau, khẳng định nào sai?

A. Mẫu chung của hai phân số đã cho là 700

B. Mẫu chung của hai phân số đã cho là 500

C. Mẫu chung của hai phân số đã cho là 1400

D. Mẫu chung của hai phân số đã cho là 2100

Xem đáp án

Đáp án là B

Mẫu chung của hai phân số sẽ là bội chung của 28 và 50

28 = $2^{2}$ .7; 50 = 2. $5^{2}$ ⇒ BCNN(28;50) = $2^{2}$ . $5^{2}$ .7 = 700

⇒ BC(28;50) = B(700)

Ta thấy 500 không phải là bội của 700 do đó, đáp án B sai

Câu 6:

Quy đồng mẫu hai phân số $\frac{5.4 + 5.7}{3.10 + 15}; \frac{6.9 - 2.17}{53.3 - 119}$ ta được:

A. $\frac{11}{18}; \frac{9}{18}$

B. $\frac{11}{18}; \frac{3}{18}$

C. $\frac{22}{18}; \frac{9}{18}$

D. $\frac{22}{18}; \frac{3}{18}$

Xem đáp án

Đáp án là C

Câu 7:

Viết các phân số sau dưới dạng phân số có mẫu là 16: $1; - 2; \frac{- 3}{4}; 0$

A. $\frac{1}{16}; \frac{- 2}{16}; \frac{- 3}{16}; \frac{0}{16}$

B. $\frac{16}{16}; \frac{- 32}{16}; \frac{- 3}{16}; \frac{0}{16}$

C. $\frac{1}{16}; \frac{- 32}{16}; \frac{- 9}{16}; \frac{0}{16}$

D. $\frac{16}{16}; \frac{- 32}{16}; \frac{- 12}{16}; \frac{0}{16}$

Xem đáp án

Đáp án là D

Câu 8:

Trong các khẳng định sau, khẳng định nào đúng?

A. Các phân số $\frac{3}{5}$ và $\frac{9}{7}$ có thể quy đồng mẫu thành $\frac{9}{5}$ và $\frac{9}{7}$

B. Các phân số $\frac{1}{3}; \frac{5}{6}; \frac{2}{5}$ có thể quy đồng mẫu thành $\frac{10}{30}; \frac{25}{30}; \frac{12}{30}$

C. Các phân số $\frac{1}{8}; \frac{5}{6}; \frac{3}{5}$ có thể quy đồng mẫu thành $\frac{12}{120}; \frac{100}{120}; \frac{24}{120}$

D. Các phân số $\frac{1}{21}; \frac{2}{7}; \frac{3}{25}$ có thể quy đồng mẫu thành $\frac{35}{520}; \frac{75}{520}; \frac{28}{520}$

Xem đáp án

Đáp án là B

Quy đồng mẫu là đưa các phân số về chung một mẫu do đó đáp án A sai.

Câu 9:

Viết các phân số sau dưới dạng phân số có mẫu là 36: $\frac{- 1}{3}; \frac{2}{3}; \frac{10}{60}; \frac{- 6}{24}$

A. $\frac{- 1}{36}; \frac{2}{36}; \frac{10}{36}; \frac{- 6}{36}$

B. $\frac{- 12}{36}; \frac{24}{36}; \frac{15}{36}; \frac{- 9}{36}$

C. $\frac{- 12}{36}; \frac{24}{36}; \frac{6}{36}; \frac{- 9}{36}$

D. $\frac{- 12}{36}; \frac{24}{36}; \frac{6}{36}; \frac{- 6}{36}$

Xem đáp án

Đáp án là C

Câu 10:

Mẫu chung nhỏ nhất của các phân số $\frac{3}{12}; \frac{- 5}{8}; \frac{4}{3}; \frac{11}{24}$ là:

A. 48

B. 72

C. 36

D. 24

Xem đáp án

Đáp án là D

Ta có: 24 ⋮ 12; 24 ⋮ 8; 24 ⋮ 3 ⇒ BCNN(12; 8; 3; 24) = 24

Mẫu chung nhỏ nhất của các phân số chính là BCNN của các mẫu số

Câu 11:

So sánh $A = \frac{2^{5} .7 + 2^{5}}{2^{5} {.5}^{2} - 2^{5} .3}$ và $B = \frac{3^{4} .5 - 3^{6}}{3^{4} .13 + 3^{4}}$ với 1.

A. A < 1 < B

B. A = B = 1

C. A > 1 > B

D. 1 > A > B

Xem đáp án

Đáp án cần chọn là: D

$\begin{array}{l} A = \frac{2^{5} .7 + 2^{5}}{2^{5} {.5}^{2} - 2^{5} .3} = \frac{2^{5} . (7 + 1)}{2^{5} . (5^{2} - 3)} \\ = \frac{2^{5} . (7 + 1)}{2^{5} . (25 - 3)} = \frac{2^{5} .8}{2^{5} .22} = \frac{8}{22} = \frac{4}{11} \\ B = \frac{3^{4} .5 - 3^{6}}{3^{4} .13 + 3^{4}} = \frac{3^{4} . (5 - 3^{2})}{3^{4} . (13 + 1)} \\ = \frac{3^{4} . (5 - 9)}{3^{4} .14} = \frac{3^{4} . (- 4)}{3^{4} .14} \\ = \frac{- 4}{14} = \frac{- 2}{7} \end{array}$

MSC = 77

$\begin{array}{l} \frac{4}{11} = \frac{4.7}{11.7} = \frac{28}{77}; \\ \frac{- 2}{7} = \frac{- 2.11}{7.11} = \frac{- 22}{77} \end{array}$

Do đó $\frac{- 22}{77} < \frac{28}{77} < 1$ hay B < A < 1

Câu 12:

Có bao nhiêu phân số lớn hơn $\frac{1}{6}$ nhưng nhỏ hơn $\frac{1}{4}$ mà có tử số là 5.

A. 9

B. 10

C. 11

D. 12

Xem đáp án

Đáp án cần chọn là: A

Gọi phân số cần tìm là $\frac{5}{x}$ (x∈N*)

Ta có:

$\begin{array}{l} \frac{1}{6} < \frac{5}{x} < \frac{1}{4} \\ \Rightarrow \frac{5}{30} < \frac{5}{x} < \frac{5}{20} \\ \Rightarrow 30 > x > 20 \end{array}$

hay x∈{21;22;...;29}

Số giá trị của x là: (29 − 21):1 + 1 = 9

Vậy có tất cả 9 phân số thỏa mãn bài toán.

Câu 13:

Có bao nhiêu phân số lớn hơn $\frac{1}{3}$ nhưng nhỏ hơn $\frac{1}{2}$ mà có tử số là 6.

A. 9

B. 5

C. 25

D. 2

Xem đáp án

Đáp án cần chọn là: B

Gọi phân số cần tìm là $\frac{6}{x}$ (x∈N∗)

Ta có:

$\begin{array}{l} \frac{1}{3} < \frac{6}{x} < \frac{1}{2} \\ \Rightarrow \frac{6}{18} < \frac{6}{x} < \frac{6}{12} \\ \Rightarrow 18 > x > 12 \end{array}$

hay x∈{13;14;...;17}

Số giá trị của x là: (17 − 13):1 + 1 = 5

Vậy có tất cả 5 phân số thỏa mãn bài toán.

Câu 14:

Tìm một phân số có mẫu là 13, biết rằng giá trị của nó không thay đổi khi ta cộng tử với - 20 và nhân mẫu với 5.

A. $\frac{10}{13}$

B. $\frac{7}{13}$

C. $\frac{- 5}{13}$

D. $\frac{- 10}{13}$

Xem đáp án

Đáp án cần chọn là: C

Gọi phân số cần tìm là $\frac{a}{13} (a \in Z)$

Theo yêu cầu bài toán:

$\begin{array}{l} \frac{a}{13} = \frac{a + (- 20)}{13.5} \\ \frac{a .5}{13.5} = \frac{a + (- 20)}{13.5} \\ a .5 = a + (- 20) \\ a .5 - a = - 20 \\ a .4 = - 20 \\ a = (- 20) : 4 \\ a = - 5 \end{array}$

Vậy phân số cần tìm là $\frac{- 5}{13}$

Câu 15:

Tìm phân số có tử 14 biết rằng nếu thêm 6 đơn vị vào tử số và thêm 21 đơn vị vào mẫu số thì giá trị của phân số $\frac{a}{b}$ không đổi?

A. $\frac{14}{39}$

B. $\frac{14}{53}$

C. $\frac{14}{33}$

D. $\frac{14}{49}$

Xem đáp án

Đáp án cần chọn là: D

Gọi phân số cần tìm là $\frac{14}{a}$ ;a∈Z

Theo yêu cầu bài toán:

$\begin{array}{l} \frac{14}{a} = \frac{14 + 6}{a + 21} \\ \frac{14. (a + 21)}{a . (a + 21)} = \frac{20 a}{a . (a + 21)} \\ 14 a + 294 = 20 a \\ 14 a - 20 a = - 294 \\ - 6 a = - 294 \\ a = 49 \end{array}$

Vậy phân số cần tìm là $\frac{14}{49}$ .

Câu 16:

So sánh các phân số $A = \frac{3535.232323}{353535.2323}$ ; $B = \frac{3535}{3534}$ ; $C = \frac{2323}{2322}$

A. A < B < C

B. A = B < C

C. A > B > C

D. A = B = C

Xem đáp án

Đáp án cần chọn là: A

$\begin{array}{l} A = \frac{3535.232323}{353535.2323} \\ = \frac{(35.101) . (23.10101)}{(35.10101) . (23.101)} = 1 \\ B = \frac{3535}{3534} = \frac{3534 + 1}{3534} \\ = \frac{3534}{3534} + \frac{1}{3534} \\ = 1 + \frac{1}{3534} \\ C = \frac{2323}{2322} = \frac{2322 + 1}{2322} \\ = \frac{2322}{2322} + \frac{1}{2322} \\ = 1 + \frac{1}{2322} \end{array}$

Vì $\frac{1}{3534} < \frac{1}{2322}$ nên B < C

Mà B > 1 nên B > A

Vậy A < B < C

Câu 17:

So sánh các phân số $A = \frac{5 (11.13 - 22.26)}{22.26 - 44.52}$ và $B = \frac{138^{2} - 690}{137^{2} - 548}$

A. A < B

B. B < A

C. A = B

D. A = −B

Xem đáp án

Đáp án cần chọn là: B

$\begin{array}{l} A = \frac{5 (11.13 - 22.26)}{22.26 - 44.52} = \frac{5}{4} \\ B = \frac{138^{2} - 690}{137^{2} - 548} = \frac{138}{137} \end{array}$

Vì $\frac{138}{137} = \frac{552}{548}; \frac{5}{4} = \frac{685}{548}$

nên $\frac{138}{137} < \frac{5}{4}$ hay B < A

Câu 18:

So sánh $A = \frac{2018^{2018} + 1}{2018^{2019} + 1}$ và $\frac{2018^{2017} + 1}{2018^{2018} + 1}$ .

A. A < B

B. A = B

C. A > B

D. Không kết luận được

Xem đáp án

Đáp án cần chọn là: A

Dễ thấy A < 1 nên:

$\begin{array}{l} A = \frac{2018^{2018} + 1}{2018^{2019} + 1} < \frac{(2018^{2018} + 1) + 2017}{(2018^{2019} + 1) + 2017} \\ = \frac{2018^{2018} + 2018}{2018^{2019} + 2018} = \frac{2018. (2018^{2017} + 1)}{2018. (2018^{2018} + 1)} \\ = \frac{2018^{2017} + 1}{2018^{2018} + 1} = B \end{array}$

Vậy A < B

Câu 19:

So sánh $A = \frac{2003^{2003} + 1}{2003^{2004} + 1}$ và $\frac{2003^{2002} + 1}{2003^{2003} + 1}$ .

A. A < B

B. A = B

C. A > B

D. Không kết luận được

Xem đáp án

Đáp án cần chọn là: A

Dễ thấy A < 1 nên:

$\begin{array}{l} A = \frac{2003^{2003} + 1}{2003^{2004} + 1} < \frac{2003^{2003} + 1 + 2002}{2003^{2004} + 1 + 2002} \\ = \frac{2003^{2003} + 2003}{2003^{2004} + 2003} = \frac{2003. (2003^{2002} + 1)}{2003 (2003^{2003} + 1)} \\ = \frac{2003^{2002} + 1}{2003^{2003} + 1} = B \end{array}$

Vậy A < B.

Câu 20:

Cho $A = \frac{36.85.20}{25.84.34}$ và $B = \frac{30.63.65.8}{117.200.49}$ . Chọn câu đúng.

A. A < B

B. A = B

C. A > 1;B < 0

D. A > B

Xem đáp án

Đáp án cần chọn là: B

$\begin{array}{l} A = \frac{36.85.20}{25.84.34} \\ = \frac{6.6.17.5.4.5}{5.5.6.2.7.17.2} \\ = \frac{{6.6.17.4.5}^{2}}{{7.6.17.4.5}^{2}} = \frac{6}{7} \\ B = \frac{30.63.65.8}{117.200.49} \\ = \frac{6.5.7.9.13.5.4.2}{13.9.20.10.7.7} \\ = \frac{6.7.10.20.9.13}{7.7.10.20.9.13} = \frac{6}{7} \end{array}$

Suy ra A = B.

Câu 21:

Số các cặp số nguyên (x;y) thỏa mãn $\frac{1}{18} < \frac{x}{12} < \frac{y}{9} < \frac{1}{4}$ là:

A. 2

B. 3

C. 1

D. 4

Xem đáp án

Đáp án cần chọn là: B

MSC:36

Khi đó:

$\begin{array}{l} \frac{1}{18} < \frac{x}{12} < \frac{y}{9} < \frac{1}{4} \\ \Rightarrow \frac{2}{36} < \frac{x .3}{36} < \frac{y .4}{36} < \frac{9}{36} \\ \Rightarrow 2 < x .3 < y .4 < 9 \end{array}$

Mà (x.3)⋮3 và (y.4)⋮4 nên x.3∈{3;6} và y.4∈{4;8}
Mà x.3 < y.4 nên:

+ Nếu x.3 = 3 thì y.4 = 4 hoặc y.4 = 8

Hay nếu x = 1 thì y = 1 hoặc y = 2

+ Nếu x.3 = 6 thì y.4 = 8

Hay nếu x = 2 thì y = 2

Vậy các cặp số nguyên (x;y) là (1;1),(1;2),(2;2)

Câu 22:

Số các cặp số nguyên (x;y) thỏa mãn $\frac{1}{24} < \frac{x}{8} < \frac{y}{4} < \frac{1}{2}$ là

A. 2

B. 3

C. 1

D. 4

Xem đáp án

Đáp án cần chọn là: C

MSC:24

Khi đó:

$\begin{array}{l} \frac{1}{24} < \frac{x}{8} < \frac{y}{4} < \frac{1}{2} \\ \Rightarrow \frac{1}{24} < \frac{3 x}{24} < \frac{6 y}{24} < \frac{12}{24} \\ \Rightarrow 1 < 3 x < 6 y < 12 \end{array}$

Mà (x.3)⋮3 và (y.6)⋮6 nên x.3∈{3;6} và y.6=6

Nên ta có x = 1;x = 2 và y = 1

Mà 1 < 3x < 6y < 12

Vậy có một cặp số nguyên là: (x;y) là (1;1).