Trắc nghiệm Các dạng toán về số nguyên tố, hợp số , phân tích một số ra thừa số nguyên tố (có đáp án)
Trắc nghiệm Các dạng toán về số nguyên tố, hợp số , phân tích một số ra thừa số nguyên tố (có đáp án)
-
1008 lượt thi
-
20 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Chọn khẳng định đúng:
Xem đáp án
A. Đáp án này đúng vì mọi số tự nhiên đều có ước chung là 1.
B. Đáp án này sai, vì 0 không là ước của 1 số nào cả.
C. Đáp án này sai, vì số nguyên tố có 2 ước là 1 và chính nó.
D. Đáp án này sai, vì 2 số nguyên tố có ước chung là 1.
Đáp án cần chọn là: A
Câu 2:
Số nguyên tố nhỏ hơn 30 là:
Xem đáp án
Các số nguyên tố nhỏ hơn 30 là: 2; 3; 5; 7; 9; 11; 13; 17; 19; 23; 29.
Số cần tìm là 23.
Đáp án cần chọn là: A
Câu 3:
Một ước nguyên tố của 91 là
Xem đáp án
91 có tổng các chữ số bằng 10 không chia hết cho 3 nên 3 không là ước nguyên tố của 91
91 có chữ số tận cùng là 1 nên 91 không chia hết cho 2, do đó 2 không là ước nguyên tố.
Một ước số nguyên tố của 91 là: 7.
Đáp án cần chọn là: D
Câu 4:
Cho a2.b.7 = 140 với a, b là các số nguyên tố, vậy a có giá trị là bao nhiêu:
Xem đáp án
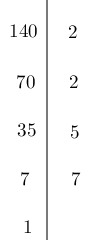
Suy ra
140 = 22.5.7 = a2.b.7 nên a = 2.
Đáp án cần chọn là: B
Câu 5:
Cho số 150 = 2.3.52, số lượng ước của 150 là bao nhiêu:
Xem đáp án
Ta có
150 = 2.3.52, vậy x = 1; y = 1; z = 2
Vậy số lượng ước của số 150 là (1+1)(1+1)(2+1) = 2.2.3 = 12
Đáp án cần chọn là: D
Câu 6:
Khi phân tích các số 2150; 1490; 2340 ra thừa số nguyên tố thì số nào có chứa tất cả các thừa số nguyên tố 2; 3 và 5?
Xem đáp án
+) Phân tích số 2150 thành thừa số nguyên tố
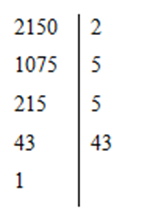
Suy ra 2150 = 2.52.43
+) Phân tích số 1490 thành thừa số nguyên tố
Suy ra 1490 = 2.5.149
+) Phân tích số 2340 thành thừa số nguyên tố
Suy ra 2340 = 22.32.5.13
Vậy có số 2340 thỏa mãn yêu cầu đề bài.
Đáp án cần chọn là: A
Câu 7:
Số 40 được phân tích thành các thừa số nguyên tố là:
Xem đáp án
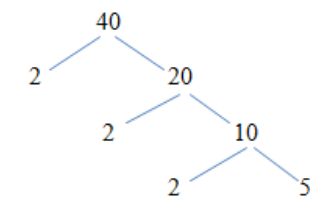
Vậy 40 = 2.2.2.5 = 23.5
Đáp án cần chọn là: D
Câu 8:
Biết 400 = 24.52. Hãy viết 800 thành tích các thừa số nguyên tố
Xem đáp án
400 = 24.52
800 = 400.2 = 2.24.52 = 25.52
Đáp án cần chọn là: B
Câu 9:
225 chia hết cho tất cả bao nhiêu số nguyên tố?
Xem đáp án
Số 225 chia hết cho các số nguyên tố: 3; 5
Vậy 225 chia hết cho 2 số nguyên tố.
Đáp án cần chọn là: D
Câu 10:
Tổng của 3 số nguyên tố là 578. Tìm ra số nguyên tố nhỏ nhất trong 3 số nguyên tố đó.
Xem đáp án
Tổng 3 số nguyên tố là 578 là số chẵn, nên trong 3 số nguyên tố có ít nhất 1 số là số chẵn. Ta đã biết số 2 là số nguyên tố chẵn duy nhất. Vậy số nguyên tố nhỏ nhất trong 3 số nguyên tố có tổng là 578 là số 2.
Đáp án cần chọn là: A
Câu 11:
Có bao nhiêu số nguyên tố x thỏa mãn 50 < x < 60?
Xem đáp án
Các số x thỏa mãn 50 < x < 60 là 51; 52; 53; 54; 55; 56; 57; 58; 59
Trong đó các số nguyên tố là 53; 59.
Vậy có hai số nguyên tố thỏa mãn đề bài.
Đáp án cần chọn là: A
Câu 12:
Tìm tất cả các số tự nhiên n để n2 + 12n là số nguyên tố.
Xem đáp án
Ta có
n2 + 12n = n(n + 12); n + 12 >1 nên để n2 + 12n là số nguyên tố thì n = 1.
Thử lại
n2 + 12n = 12 + 12.1 = 13 (nguyên tố)
Vậy với n = 1 thì n2 + 12n là số nguyên tố.
Đáp án cần chọn là: D
Câu 13:
Nếu cho 7 hình vuông đơn vị ghép thành hình chữ nhật thì có mấy cách xếp (Không kể việc xoay chiều dài và chiều rộng)?
Xem đáp án
Nếu xếp 7 hình vuông đơn vị thành hình chữ nhật thì chiều rộng của hình chữ nhật chỉ có thể xếp:
Đáp án cần chọn là: A
Câu 14:
Tích của hai số tự nhiên bằng 105. Có bao nhiêu cặp số thỏa mãn?
Xem đáp án
Gọi hai số tự nhiên cần tìm là a và b (a; b ∈ N)
Ta có a.b = 105
Phân tích số 105 ra thừa số nguyên tố ta được 105 = 3.5.7
Các số a; b là ước của 105 , do đó ta có
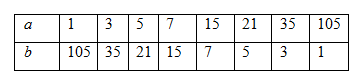
Vậy có 8 cặp số thỏa mãn yêu cầu.
Đáp án cần chọn là: D
Câu 15:
Số 360 khi phân tích được thành thừa số nguyên tố, hỏi tích đó có bao nhiêu thừa số là số nguyên tố?
Xem đáp án
Ta có
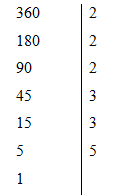
Nên 360 = 23.32.5
Vậy có thừa số nguyên tố sau khi phân tích là 2; 3 và 5.
Đáp án cần chọn là: A
Câu 16:
Số các ước của số 192 là
Xem đáp án
Ta có
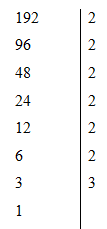
Nên
192=26.3 nên số ước của 192 là
(6+1)(1+1) = 14 ước.
Đáp án cần chọn là: C
Câu 17:
Một hình vuông có diện tích là 1936m2. Tính cạnh của hình vuông đó.
Xem đáp án
Phân tích số 1936 ra thừa số nguyên tố ta được
Hay 1936 = 24.112 = (22.11).(22.11) = 44.44
Vậy cạnh hình vuông bằng 44m.
Đáp án cần chọn là: A
Câu 18:
Xem đáp án
Đặt p = 3a + r (r = 0; 1; 2; a∈N)
Với r = 1 ta có p + 8 = 3a + r + 8 = (3a + 9)⋮3, (3a + 9) >3 nên p + 8 là hợp số.
Do đó loại r = 1.
Với r = 2 ta có p + 4 = 3a + r + 4 = (3a + 6)⋮3, (3a + 6) >3 nên p + 4 là hợp số.
Do đó loại r = 2.
Do đó r = 0; p = 3a là số nguyên tố nên a = 1 ⇒ p = 3.
Ta có p + 4 = 7; p + 8 = 11 là các số nguyên tố.
Vậy p = 3.
Có một số nguyên tố pp thỏa mãn đề bài.
Đáp án cần chọn là: B
Câu 19:
Cho nguyên tố p chia cho 42 có số dư r là hợp số. Tìm r.
Xem đáp án
Ta có p = 42.a + r = 2.3.7.a + r (a, r∈N; 0 < r < 42)
Vì p là số nguyên tố nên r không chia hết cho 2; 3; 7.
Các hợp số nhỏ hơn 42 không chia hết cho 2 là 9; 15; 21; 25; 27; 33; 35; 39
Loại bỏ các số chia hết cho 3 và 7 ta còn số 25.
Vậy r = 25.
Đáp án cần chọn là: D
Câu 20:
Cho phép tính \[\overline {ab} .c = 424\]. Khi đó cc bằng bao nhiêu?
Xem đáp án
Vì \[\overline {ab} .c = 424\] là ước có hai chữ số của 424.
Phân tích số 424 ra thừa số nguyên tố ta được
Hay 424=23.53
Các ước của 424 là 1; 2; 4; 8; 53; 106; 212; 424
Suy ra \[\overline {ab} = 53\] suy ra c = 424:53 = 8.
Đáp án cần chọn là: B