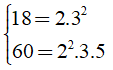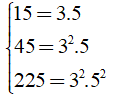Bài tập: Ước chung lớn nhất. Bội chung nhỏ nhất chọn lọc, có đáp án
-
2000 lượt thi
-
16 câu hỏi
-
15 phút
Danh sách câu hỏi
Câu 1:
Tìm ƯCLN ( 16, 32, 112)?
 Xem đáp án
Xem đáp án
Đáp án là C
Ta có 32 ⋮ 16; 112 ⋮ 16 ⇒ ƯCLN ( 16; 32; 112) = 16
Câu 3:
ƯCLN của a và b là:
 Xem đáp án
Xem đáp án
Đáp án là A
Nếu a chia hết cho b thì b là ước của a.
Mà b cũng là ước của b nên b ∈ ƯC(a; b)
Hơn nữa b là ước chung lớn nhất của b nên ƯCLN(a; b) = b
Câu 5:
Cho a = .5.7 và b = .3.7. Tìm ƯCLN của a và b
 Xem đáp án
Xem đáp án
Đáp án là A
Ta có: a = .5.7 và b = .3.7 nên ƯCLN(a, b) = 3.7
Câu 6:
Số tự nhiên a lớn nhất thỏa mãn 90 ⋮ a và 135 ⋮ a là:
 Xem đáp án
Xem đáp án
Đáp án là C
Vì 90 ⋮ a và 135 ⋮ a ⇒ a ∈ ƯC (90, 135)
Vì a là số lớn nhất thỏa mãn điều kiện trên nên a = ƯCLN (90; 135)
90 = 2..5
135 = .5
⇒ ƯCLN (90, 135) = .5 = 45
Câu 7:
Một đội ý tế có 36 bác sĩ và 108 y tá. Có thể chia đội y tế đó nhiều nhất thành mấy tổ để các bác sĩ cũng như các y tá được chia đều vào mỗi tổ?
 Xem đáp án
Xem đáp án
Đáp án là A
Gọi số tổ có thể chia là a
Vì các bác sĩ và y tá được chia đều vào mỗi tổ nên 36 ⋮ a và 108 ⋮ a và a lớn nhất. Do đó, a là ƯCLN (36; 108)
Vì 108 ⋮ 36 nên ƯCLN (36, 108) = 36
Câu 8:
Trong hai số sau, hai số nào là hai số nguyên tố cùng nhau:
 Xem đáp án
Xem đáp án
Đáp án là B
Ta có:
ƯC ( 2, 6) = {1; 2}
ƯC (3, 10) = {1}
ƯC ( 6, 9) = {1; 3}
ƯC ( 15, 33) = {1; 3}
Chú ý: Hai số gọi là nguyên tố cùng nhau nếu chúng có ước chung duy nhất là 1.
Câu 9:
Tìm số tự nhiên x, biết rằng 162 ⋮ x; 360 ⋮ x và 10 < x < 20 :
 Xem đáp án
Xem đáp án
Đáp án là C
Vì 162 ⋮ x; 360 ⋮ x ⇒ x ∈ ƯC (162, 360)
Ta có:
162 = 2.
360 = ..5
Suy ra, ƯCLN ( 162, 360) = 2. = 18
ƯC ( 162, 360) = Ư (18) = {1, 2, 3, 6, 9, 18} ⇒ x ∈ {1, 2, 3, 6, 9, 18}
Vì 10 < x < 20 ⇒ x = 18
Câu 10:
Lớp 9A có 45 học sinh, lớp 9B có 42 học sinh, lớp 9C có 48 học sinh. Trong ngày khai giảng, ba lớp cùng xếp thành một số hàng dọc như nhau để diễu hành mà không lớp nào có người lẻ hàng. Số hàng dọc nhiều nhất có thể xếp được là:
 Xem đáp án
Xem đáp án
Đáp án là B
Gọi a là số hàng dọc nhiều nhất có thể xếp được

Suy ra ƯCLN(45;42;48) = 3
Vậy có thể xếp được nhiều nhất 3 hàng dọc.
Câu 13:
Một lớp học có 18 nam và 24 nữ được chia đều vào các nhóm sao cho số nam trong các nhóm bằng nhau và số nữ trong các nhóm bằng nhau. Hỏi chia được nhiều nhất bao nhiêu nhóm?
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
Câu 14:
Một lớp học có 20 nam và 25 nữ được chia đều vào các nhóm sao cho số nam trong các nhóm bằng nhau và số nữ trong các nhóm bằng nhau. Hỏi chia được nhiều nhất bao nhiêu nhóm?
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Câu 15:
Lớp 6A có 40 học sinh, lớp 6B có 48 học sinh, lớp 6C có 32 học sinh. Ba lớp cùng xếp thành hàng như nhau và không lớp nào lẻ hàng. Tính số hàng dọc nhiều nhất mỗi lớp có thể xếp được?
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
Câu 16:
Lớp 6A có 36 học sinh, lớp 6B có 54 học sinh, lớp 6C có 45 học sinh. Ba lớp cùng xếp thành hàng như nhau và không lớp nào lẻ hàng. Tính số hàng dọc nhiều nhất mỗi lớp có thể xếp được?
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
Số hàng dọc nhiều nhất có thể xếp được là ước chung lớn nhất của 36; 54; 45
36=;
Khi đó, UCLN (36;54;45) = 9
Vậy số hàng dọc nhiều nhất mỗi lớp xếp được là 9 hàng.