Đề kiểm tra Giữa học kì 1 Toán 6 có đáp án (Đề 2)
-
1201 lượt thi
-
12 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
I. Phần trắc nghiệm (4 điểm)
Tập hợp A các số tự nhiên x thỏa mãn 4 < x ≤ 9 là:
Xem đáp án
Các số tự nhiên x thỏa mãn 4 < x ≤ 9 hay x lớn hơn 4 và nhỏ hơn hoặc bằng 9 là: 5, 6, 7, 8, 9.
Ta viết tập hợp A bằng cách liệt kê các phần tử ta được: A = {5; 6; 7; 8; 9}.
Ta viết tập hợp A bằng cách nêu dấu hiệu đặc trưng: A = {x \( \in \mathbb{N}\)| 4 < x ≤ 9}.
Chọn đáp án B.
Câu 2:
Xem đáp án
Sử dụng sàng Eratosthenes ta đã biết các số nguyên tố nhỏ hơn 25 là: 2, 3, 5, 7, 11, 13, 17, 19, 23.
Vậy có 9 số nguyên tố nhỏ hơn 25.
Câu 3:
Xem đáp án
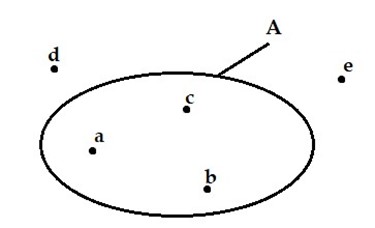
Quan sát hình vẽ: (đây là sơ đồ Ven)
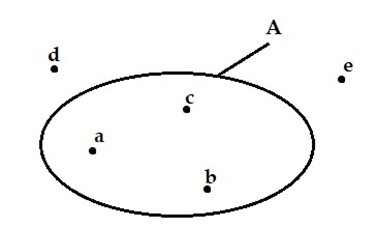
Ta thấy
+ Các phần tử a, b, c nằm trong vòng kín biểu diễn tập hợp A, nên các phần tử a, b, c đều thuộc tập hợp A, ta viết \(a \in A,b \in A,c \in A\).
+ Các phần tử d, e nằm ngoài vòng kín biểu diễn tập hợp A nên các phần tử này không thuộc tập hợp A, ta viết \(d \notin A,e \notin A.\)
Vậy đáp án A đúng.
Chọn đáp án A.
Câu 4:
Xem đáp án
Để tìm các ước của 16, ta lấy 16 lần lượt chia cho các số tự nhiên từ 1 đến 16, các phép chia hết là: 16 : 1 = 16, 16 : 2 = 8, 16 : 4 = 4, 16 : 8 = 2, 16 : 16 = 1.
Vậy các ước của 16 là: 1, 2, 4, 8, 16.
Ta viết tập hợp A các ước của 16 là A = {1; 2; 4; 8; 16}.
Câu 5:
Xem đáp án
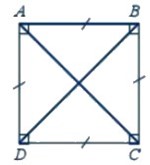
Hình vuông ABCD có các tính chất:
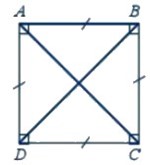
+ Bốn cạnh bằng nhau: AB = BC = CD = DA
+ Hai cạnh đối AB và CD, BC và AD song song với nhau
+ Hai đường chéo bằng nhau: AC = BD
+ Bốn góc ở các đỉnh A, B, C, D là góc vuông.
Vậy hình vuông đã cho không có tính chất AD và CD song song với nhau.
Chọn đáp án C.
Câu 6:
Xem đáp án
Số mét dây cần uốn chính là chu vi của hình thoi có độ dài cạnh bằng 25 cm và là:
P = 4 . 25 = 100 cm = 1 m
Vậy bác Hà cần 1 m dây thép để uốn.
Chọn đáp án C.
Câu 7:
Xem đáp án
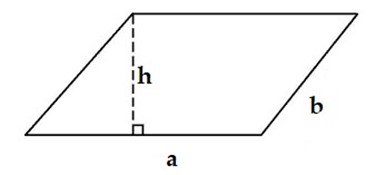
Cho hình bình hành
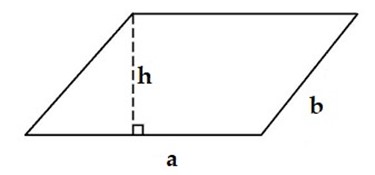
Diện tích của hình bình hành là S = a . h.
Câu 8:
Xem đáp án
Vì mỗi thuyền chỉ chở được 6 người cả người lái đò nên mỗi thuyền chở được 5 người khách (trừ người lái đò).
Có tất cả 52 người khách. Ta thực hiện phép chia: 52 : 5 = 10 (dư 2)
Do đó dùng 10 thuyền để chở được 50 người khách và dư 2 người nên cần thêm một thuyền nữa để chở 2 người đó.
Vậy cần ít nhất 10 + 1 = 11 thuyền để chở hết số khách.
Chọn đáp án C.
Câu 9:
II. Phần tự luận (6 điểm)
1) Thực hiện các phép tính:
a) 25 . 8 – 15 . 5 + 160 : 16 – 10;
b) 2 . 52 – 3 : 710 + 54 : 33.
2) Phân tích các số 84, 120, 210 ra thừa số nguyên tố.
Xem đáp án
1)
a) 25 . 8 – 15 . 5 + 160 : 16 – 10
= 25 . 8 – 3 . 5 . 5 + 10 – 10
= 25 . 8 – 25 . 3 + (10 – 10)
= 25 . (8 – 3) + 0 = 25 . 5 = 125
b) 2 . 52 – 3 : 710 + 54 : 33
= 2 . 25 – 3 : 1 + 54 : 27
= 50 – 3 + 2
= 47 + 2 = 49
2)
Ta phân tích các số ra thừa số nguyên tố bằng cách viết theo cột dọc hoặc rẽ nhánh.
Vậy:
84 = 2 . 2 . 3 . 7 = 22 . 3 . 7
120 = 2 . 2 . 2 . 3 . 5 = 23 . 3 . 5
210 = 2 . 3 . 5 . 7
Câu 10:
Xem đáp án
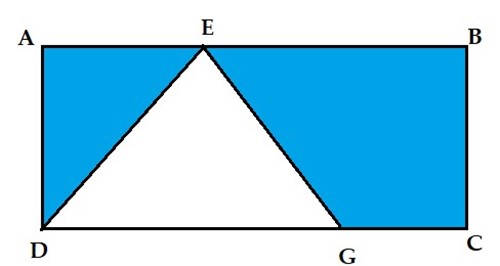
Diện tích hình chữ nhật ABCD là: AB . BC = 12 . 4 = 48 (cm2)
Diện tích hình tam giác DEG là: DG . BC : 2 = 9 . 4 : 2 = 18 (cm2) (đường cao xuất phát từ E của tam giác DEG có độ dài bằng BC)
Diện tích phần tô màu là: 48 – 18 = 30 (cm2)
Đáp số: 30 cm2.
Câu 11:
Xem đáp án
Gọi số hộp chia được là x (x là số tự nhiên khác 0)
Vì số bánh nướng trong mỗi hộp bằng nhau nên 40 ⁝ x.
Vì số bánh dẻo trong mỗi hộp bằng nhau nên 30 ⁝ x.
Vì x là số hộp bánh lớn nhất chia được nên x = ƯCLN(30, 40)
Ta có 30 = 2 . 3 . 5 và 40 = 23 . 5 nên ƯCLN(30, 40) = 2 . 5 = 10
Hay x = 10 (thỏa mãn)
Vậy số hộp bánh chia được nhiều nhất là 10 hộp.
Câu 12:
Xem đáp án
Vì 3n + 4 = 3n + 7 – 3 = 3n – 3 + 7 = 3(n – 1) + 7
Do 3(n – 1) chia hết cho n – 1 (tính chất chia hết của một tích)
Nên để 3n + 4 chia hết cho n – 1 thì 7 phải chia hết cho n – 1 (tính chất chia hết của một tổng)
Hay (n – 1) thuộc Ư(7) = {1; 7}
Với n – 1 = 1 thì n = 2
Với n – 1 = 7 thì n = 8
Vậy với n = 2 hoặc n = 8 thì 3n + 4 chia hết cho n – 1.