Đề kiểm tra Giữa học kì 1 Toán 6 có đáp án (Đề 3)
-
1298 lượt thi
-
12 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Viết các tập hợp đã cho dưới dạng liệt kê các phần tử ta được
A = {4; 5; 6; … } (tập hợp A các số tự nhiên lớn hơn 3)
B = {0; 1; 2; 3; 4; 5} (tập hợp B các số tự nhiên nhỏ hơn 6)
C = {0; 1; 2; 3; 4} (tập hợp C các số tự nhiên nhỏ hơn hoặc bằng 4)
D = {5; 6; 7; 8} (tập hợp D các số tự nhiên lớn hơn 4 và nhỏ hơn hoặc bằng 8)
Vậy ta thấy tập hợp C có 5 phần tử.
Chọn đáp án C.
Câu 2:
 Xem đáp án
Xem đáp án
Tập hợp M gồm các số tự nhiên lớn hơn 14, nhỏ hơn 45 và có chứa chữ số 3.
Ta thấy các số 13, 23, 33, 43 đều có chứa chữ số 3, nhưng 13 < 14 nên 13 không thuộc tập hợp M.
Chọn đáp án A.
Câu 3:
 Xem đáp án
Xem đáp án
Số 1080 có chữ số tận cùng là 0 nên nó chia hết cho cả 2 và 5.
Số 1080 có tổng các chữ số là 1 + 0 + 8 + 0 = 9 chia hết cho 3 và 9 nên nó chia hết cho cả 3 và 9.
Ngoài ra: 1080 : 4 = 270; 1080 : 6 = 180; 1080 : 8 = 135; 1080 : 12 = 90; 1 080 : 24 = 45; 1080 : 25 = 43 (dư 5).
Vậy số 1080 chia hết cho các số: 2, 3, 4, 5, 6, 8, 9, 12, 24.
Do đó nó chia hết cho 9 số trong các số đã cho.
Chọn đáp án B.
Câu 4:
 Xem đáp án
Xem đáp án
Mỗi hộp có 8 ngôi sao nên ta thực hiện phép chia:
97 : 8 = 12 (dư 1)
Vậy còn thừa 1 ngôi sao không xếp vào hộp.
Chọn đáp án B.
Câu 5:
 Xem đáp án
Xem đáp án
Ta phân tích 154 ra thừa số nguyên tố:
Vậy 154 = 2 . 7 . 11.
Chọn đáp án A.
Câu 6:
 Xem đáp án
Xem đáp án
Tam giác đều là hình tam giác có 3 cạnh bằng nhau và 3 góc bằng nhau, vậy trong các hình đã cho, hình vẽ D chỉ tam giác đều.
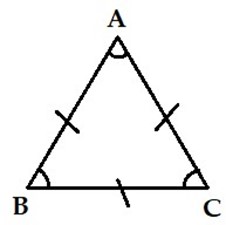
Chọn đáp án D.
Câu 7:
 Xem đáp án
Xem đáp án
Diện tích hình thoi bằng \(\frac{1}{2}\) tích độ dài hai đường chéo.
Vậy diện tích của hình thoi có độ dài hai đường chéo lần lượt là 16 cm và 12 cm là:
\(S = \frac{1}{2}.16.12 = 96\) (cm2).
Chọn đáp án B.
Câu 8:
Chọn câu sai trong các câu dưới đây?
Cho hình vẽ
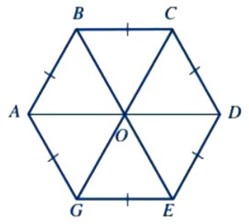
Lục giác đều ABCDEG là hình có:
 Xem đáp án
Xem đáp án
Lục giác đều ABCDEG có các tính chất:
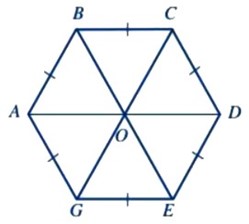
+ Các góc ở các đỉnh A, B, C, D, E, G bằng nhau.
+ Sáu cạnh bằng nhau: AB = BC = CD = DE = EG = GA.
+ Ba đường chéo chính AD, BE, CG cắt nhau tại điểm O.
+ Ba đường chéo chính bằng nhau: AD = BE = CG.
Vậy đáp án A sai (vì góc ở đỉnh O không bằng các góc ở đỉnh của lục giác).
Chọn đáp án A.
Câu 9:
II. Phần tự luận (6 điểm)
1) Thực hiện các phép tính:
a) 30 . 75 + 25 . 30 – 150;
b) 160 – (4 . 52 – 3 . 23);
c) [36 . 4 – 4 . (82 – 7 . 11)2] : 4 – 20220.
2) Tìm BCNN của các số 28, 54.
 Xem đáp án
Xem đáp án
1)
a) 30 . 75 + 25 . 30 – 150
= 30 . (75 + 25) – 150
= 30 . 100 – 150
= 3 000 – 150 = 2 850
b) 160 – (4 . 52 – 3 . 23)
= 160 – (4 . 25 – 3 . 8)
= 160 – (100 – 24)
= 160 – 76 = 84
c) [36 . 4 – 4 . (82 – 7 . 11)2] : 4 – 20220
= [36 . 4 – 4 . (82 – 77)2] : 4 – 1
= [36 . 4 – 4 . 52] : 4 – 1
= [36 . 4 – 4 . 25] : 4 – 1
= [4 . (36 – 25)] : 4 – 1
= 4 . 11 : 4 – 1 = 11 – 1 = 10
2)
Đề tìm BCNN của 28 và 54, ta phân tích các số đó ra thừa số nguyên tố.
Ta có: 28 = 4 . 7 = 22 . 7
54 = 6 . 9 = 2 . 3 . 32 = 2 . 33
Vậy BCNN(28, 54) = 22 . 33 . 7 = 4 . 27 . 7 = 756.
Câu 10:
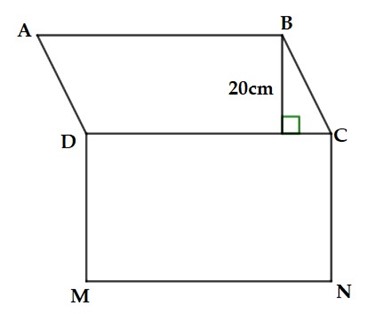
 Xem đáp án
Xem đáp án
Nửa chu vi hình chữ nhật DCNM là: 180 : 2 = 90 (cm)
Khi đó: MN + CN = 90 (cm)
Chiều dài MN gấp 4 lần chiều rộng CN
Tổng số phần bằng nhau là: 1 + 4 = 5 (phần)
Chiều dài MN (hay CD) của hình chữ nhật DCNM là: 90 : 5 . 4 = 72 (cm)
Chiều rộng CN (hay DM) của hình chữ nhật DCNM là: 90 – 72 = 18 (cm)
Diện tích hình chữ nhật DCMN là: 18 . 72 = 1 296 (cm2)
Diện tích hình bình hành ABCD là: 72 . 20 = 1 440 (cm2)
Diện tích hình H là: 1 296 + 1 440 = 2 736 (cm2).
Câu 11:
 Xem đáp án
Xem đáp án
Gọi x là số tổ nhiều nhất được chia (x là số tự nhiên khác 0).
Vì số bác sĩ được chia đều vào mỗi tổ nên 48 ⁝ x
Số y tá được chia đều vào mỗi tổ nên 108 ⁝ x
Do đó x là ước chung của 48 và 108, mà x là nhiều nhất nên x là ƯCLN của 48 và 108.
Ta có: 48 = 24 . 3
108 = 22 . 33
Suy ra ƯCLN(48, 108) = 22 . 3 = 12 hay x = 12 (thỏa mãn).
Vậy có thể chia được nhiều nhất 12 tổ.
Câu 12:
 Xem đáp án
Xem đáp án
A = 2 + 22 + 23 + 24 + … + 2100
A = (2 + 22) + (23 + 24) + … + (299 + 2100)
A = 6 + 22 . (2 + 22) + … + 298 . (2 + 22)
A = 6 + 22 . 6 + … + 298 . 6
A = 6 . (1 + 22 + … + 298)
Vậy A chia hết cho 6 (theo tính chất chia hết của một tích).
